Abstract
We introduce the concept of spatio-temporal steering (STS), which reduces, in special cases, to Einstein-Podolsky-Rosen steering and the recently-introduced temporal steering. We describe two measures of this effect referred to as the STS weight and robustness. We suggest that these STS measures enable a new way to assess nonclassical correlations in an open quantum network, such as quantum transport through nano-structures or excitation transfer in a complex biological system. As one of our examples, we apply STS to check nonclassical correlations among sites in a photosynthetic pigment-protein complex in the Fenna-Matthews-Olson model.
Similar content being viewed by others
Introduction
Quantum steering is an intriguing quantum phenomenon, which enables one party (usually referred to as Alice) to use her different measurement settings to remotely prepare the set of quantum states of another spatially-separated party (say Bob). This ability, which is not achievable without quantum resources, was first described by Schrödinger1 in his response to the work of Einstein, Podolsky, and Rosen (EPR)2 on quantum entanglement and the related question about the completeness of quantum mechanics. As recently shown3, quantum steering (also refereed to as EPR steering) is, in general, weaker than Bell’s nonlocality4, 5 but stronger than quantum entanglement6. After eighty years, quantum steering has been gradually formulated mathematically3, 7,8,9,10 and observed experimentally7, 11,12,13,14,15,16,17,18,19,20. Other developments include: using steering as a resource for quantum-information processing, quantifying steering9, 10, 21,22,23, clarifying its relationship to the problem of the incompatibility of measurements24,25,26,27,28, connecting steering with quantum computation29, 30, and multipartite quantum steering30,31,32,33,34, among various other generalizations and applications (see ref. 35 and references therein).
Nonclassical temporal correlations (like photon antibunching) play a fundamental role in quantum optics research, since the Hanbury-Brown and Twiss experiments36 and the Glauber theory of quantum coherence37. While there is as yet no clear temporal analog of quantum entanglement, attempts at defining such have led to new ideas about quantum causality (see, e.g., refs 38–40 and references therein). Recently, temporal steering41 was introduced as a temporal analog of EPR steering, which refers to a nonclassical correlation of a single object at different times. Contrary to temporal entanglement, temporal steering has a clear operational meaning29, 41,42,43,44,45,46,47. In particular, temporal steering was used for testing the security of quantum key distribution protocols41, 46 and for quantifying the non-Markovian dynamics of open systems44. Recently, temporal steering was also experimentally demonstrated47 by measuring the violation of the temporal inequality presented in ref. 41. Moreover, a measure of temporal steering was proposed44, 46 and experimentally determined47.
Here, we introduce the concept of spatio-temporal steering (STS) as a natural unification of the EPR and temporal forms of steering. In addition, we propose two measures of STS, specifically, its robustness and weight. We also show the usefulness of STS in testing and quantifying nonclassical correlations of quantum networks by analyzing two examples, including the decay of nonclassical correlations in quantum excitation transfers in the Fenna-Matthews-Olson (FMO) protein complex, which is one of the most widely studied photosynthetic complexes48. Note that STS can also be applied to test quantum-state transfer in quantum networks like those described in refs 49, 50.
Results
Temporal steering: From temporal hidden-variable model to temporal hidden-state model
Let us briefly review the so-called temporal hidden-state model for a single system at two moments of time29, 41, 44. Consider that, during the evolution of the system from time 0 to time t, one can perform measurements using different settings {x} and {y} to obtain outcomes {a} and {b} at times 0 and t, respectively. If one makes two assumptions: (A1) noninvasive measurability at time 0, which means that one can obtain a measurement outcome without disturbing the system, and (A2) macrorealism (macroscopic realism)51, which means that the outcome of the system pre-exists, no matter if a measurement has been performed or not. Under these conditions, there exist some hidden variables λ, which a priori determine the joint probability distributions52,53,54,55,56,57
Now, if one replaces the assumption (A2) with (A2’), which means that during each moment of time the system can be described by a quantum state σ λ , which is determined by some hidden variables λ independent of the measurements performed before, then the hidden variables determine not only the observed data table \(p(a|x)={\sum }_{\lambda }\,p(\lambda )p(a|x,\lambda )\) at time t = 0, but also a priori the quantum state \(\rho ={\sum }_{\lambda }\,p(\lambda ){\sigma }_{\lambda }\) at time t. It is convenient to define the temporal assemblage
where \({\tilde{\sigma }}_{a|x}(t)\) is the observed quantum state at time t conditioned on the earlier measurement event a|x at time 0. Thus, the temporal assemblage is a set of subnormalized states, which characterizes the joint behaviour: (1) \(p(a|x)={\rm{tr}}[{\sigma }_{a|x}^{{\rm{T}}}(t)]\) and (2) \({\tilde{\sigma }}_{a|x}(t)={\sigma }_{a|x}^{{\rm{T}}}(t)/{\rm{tr}}[{\sigma }_{a|x}^{{\rm{T}}}(t)]\). Furthermore, the formulation of the temporal hidden-state model can be written as
Quantum mechanics predicts some assemblages, which do not admit the temporal hidden-state model, and we refer to this situation as temporal steering 44. Note that since the hidden-state model is a strict subset of the hidden-variable model, using the former model may admit an easier detection of the nonclassicality of the quantum dynamics than using the hidden-variable model.
Spatio-temporal steering
Similarly, we can also generalize the hidden-state model to the hybrid spatio and temporal scenario. That is, we would like to consider the hidden-state model for a system B at time t, after the local measurement has been performed on a system A at time 0. Then, under the assumptions of non-invasive measurement for the system A at time 0 and the hidden state for the system B at time t, the spatio-temporal hidden-state model is written as (for brevity, the term “spatio-temporal” will be sometimes omitted hereafter).
where \({\sigma }_{a|x}^{\mathrm{ST},B}(t)\equiv {p}_{{\rm{A}}}(a|x){\tilde{\sigma }}_{a|x}^{{\rm{ST}},{\rm{B}}}(t)\), with \({\tilde{\sigma }}_{a|x}^{{\rm{ST}},{\rm{B}}}(t)\) being the observed quantum state of the system B at time t, conditioned on the measurement event a|x [with corresponding data table p A(a|x)] of the system A at time 0. When there is no risk of confusion, we will abbreviate \({\sigma }_{a|x}^{{\rm{ST}},{\rm{B}}}(t)\) as \({\sigma }_{a|x}^{{\rm{ST}}}(t)\), p A(a|x) as p(a|x), and \({\sigma }_{\lambda }^{{\rm{B}}}\) as σ λ . The set of subnormalized states \({\{{\sigma }_{a|x}^{{\rm{ST}}}(t)\}}_{a,x}\) is refereed to as a spatio-temporal assemblage having the property \(p(a|x)={\rm{tr}}[{\sigma }_{a|x}^{{\rm{ST}}}(t)]\) and \({\tilde{\sigma }}_{a|x}^{{\rm{ST}}}(t)={\sigma }_{a|x}^{{\rm{ST}}}(t)/{\rm{tr}}[{\sigma }_{a|x}^{{\rm{ST}}}(t)]\), and can be certified if it admits the model, given by equation (3), via the following semidefinite programming (SDP) (see ref. 58 for SDP, and refs 8, 9, 27 for dealing with the certification of the hidden-state model for a given assemblage):
where \({\rho }_{\lambda }\equiv p(\lambda ){\sigma }_{\lambda }\), and the notation ρ λ ≥ 0 denotes that ρ λ is a positive-semidefinite operator. Quantum mechanics predicts that
with ρ 0 being the initial quantum state shared by the systems A and B at time 0, {F a|x } a being the positive-operator-valued measure representing the measurement x. The quantum channel Λ describes the time evolution of the post-measurement composite system from time 0 to time t see the schematic diagram in Fig. 1(a).
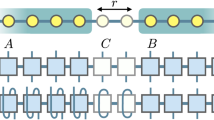
(a) Schematic diagram of spatio-temporal steering. At time t = 0, a system A (which may be entangled with a system B) is subject to a local measurement with one of the measurement settings {x}, which is described by a positive-operator-valued measure {F a|x } a . After this measurement, the post-measurement composite state ρ a|x is sent into a quantum channel Λ and evolves for a time period t. After many rounds of the experiment, the set of subnormalized quantum states of the system B is denoted as \({\{{\sigma }_{a|x}^{{\rm{ST}}}(t)\}}_{a,x}\). With some appropriate ρ 0, {F a|x } a,x , and Λ, the assemblage \({\{{\sigma }_{a|x}^{{\rm{ST}}}(t)\}}_{a,x}\) does not admit the spatio-temporal hidden-state model equation (3). We call this spatio-temporal steering and refer the assemblage \({\{{\sigma }_{a|x}^{{\rm{ST}}}(t)\}}_{a,x}\) as spatio-temporal steerable. (b) A schematic example of a quantum network with damage (strong dissipation or dephasing, or an entirely broken link). The STS weight and robustness can be employed as diagnostic tools to check whether site-A and site-B are nonclassically correlated.
With an appropriately designed ρ 0, {F a|x } a,x , and Λ, the assemblage cannot be written in the form of equation (3) i.e., there is no feasible solution of the SDP problem given in equation (4). In this situation, the assemblage is said to be spatio-temporal steerable. To quantify the degree of such steerability, we would like to introduce the quantifier called the STS weight (ST SW), which is defined as
(the same techniques have been demonstrated in refs 9, 44). \({\{{\sigma }_{a|x}^{\mathrm{ST},\mathrm{US}}(t)\}}_{a,x}\) stands for the unsteerable (US) assemblage i.e., one admits equation (3), \({\{{\sigma }_{a|x}^{\mathrm{ST},S}(t)\}}_{a,x}\) represents the steerable assemblage, and 0 ≤ μ ≤ 1. This can be formulated as the following SDP problem:
In addition, we would like to introduce another measure, referred to as the STS robustness (ST SR), which can be viewed as a generalization of the EPR steering robustness10 to the present spatio-temporal scenario. The STS robustness ST SR can be defined as the minimum noise \({\tau }_{a|x}^{{\rm{ST}}}(t)\) to be added to \({\sigma }_{a|x}^{{\rm{ST}}}(t)\), such that the mixed assemblage is unsteerable. That is, \(ST\,SR=\,{\rm{\min }}\,\alpha \,{\rm{subject}}\,{\rm{to}}\,{\{\frac{1}{1+\alpha }{\sigma }_{a|x}^{{\rm{ST}}}(t)+\frac{\alpha }{1+\alpha }{\tau }_{a|x}^{{\rm{ST}}}(t)={\sigma }_{a|x}^{\mathrm{ST},\mathrm{US}}\}}_{a,x}\). This can also be formulated as an SDP problem. Specifically,
The STS robustness and weight, analogously to their EPR counterparts, have different operational meanings and properties. For example, one could expect that these measures can imply different orderings of states, analogously to this property exhibited by various measures of entanglement59,60,61, Bell nonlocality62, and nonclassicality63. A detailed comparison of these two STS measures will be given elsewhere64. Here, we have calculated the STS weight for Example 1, and the STS robustness for Example 2 in the following sections, just to show that these measures can easily be computed and interpreted.
Examining nonclassical correlations within a quantum network
A possible application of STS is that it can be used to witness whether two nodes of a quantum network are nonclassically correlated (or quantum connected). Consider two qubits on the opposite ends of a quantum network, as shown in Fig. 1(b). There may be a damage somewhere in the network, such that the quantum coherent interaction between distant nodes may be inhibited. To verify this, one can initially perform measurements at time t A = 0 on site-A. On site-B, one performs measurements at a later time t. If the value of the STS weight (or, equivalently, the STS robustness) is always zero for the whole range of time t, one can say that the influence of the quantum measurement at site-A is not transmitted to site-B in a steerable way.
Example 1: The spatio-temporal steering weight in a three-qubit network
As an example of STS in a quantum network, let us apply a simplified model of two qubits coherently coupled via a third qubit Fig. 2(b). The interaction Hamiltonian of the entire system is
where \({\sigma }_{+}^{i}\) (\({\sigma }_{-}^{i}\)) is the raising (lowering) operator of the ith qubit respectively, while J 12 (J 23) is the coupling strength between qubits 1 (2) and 2 (3). To simulate the damage in the network, and quantify it, we assume qubit 2 may suffer noise-induced dephasing. For simplicity, the two coupling strengths are equal, i.e., \({J}_{12}={J}_{23}\equiv J\). The STS weight, calculated as described above, is plotted in Fig. 2(b). We can see that if the dephasing rate γ is very small, the STS weight oscillates with time t, revealing the coherent interaction between qubits 1 and 3 via the middle qubit. If γ is large (i.e. the middle node is damaged), one sees the growth of the STS weight at a later time. One can imagine that if the dephasing is very strong, it can inhibit the appearance of the STS weight. However, several caveats arise in that the apparent correlations may be transmitted via other means than the network itself (via some environment or eavesdropper). A possible opening for future research in this area is to consider a multi-partite extension, and whether it can be used as a measure of quantum communities in networks65.
The STS weight versus time in a simple quantum network model described in example 1 in the text. (a) Three identical qubits, with coherent coupling J 12 (J 23) between qubit 1 (2) and 2 (3). To simulate the damaged node, we assume qubit 2 suffers a phase damping γ. (b) The blue-solid, black-dashed, and red-dotted curves show the STS weight (ST SW) of the assemblage \({\{{\sigma }_{a|x}^{{\rm{ST}}}(t)\}}_{a,x}\) of qubit-3 for different dephasing rates of the middle qubit γ/J = 0.01, 1, and 20, respectively. The measurement settings {x} on qubit-1 at time 0 are the Pauli set X, Y, and Z. The initial condition is \(|1\rangle \otimes |0\rangle \otimes |0\rangle \), and \({J}_{12}={J}_{23}\equiv J\). The time t is in units of J −1. From the figure, we can see that when the dephasing rate increases from 0.01J to 1J, the amplitude of the ST SW decreases. This means that when dephasing rate increases from 1J to 20J, the dephasing mechanism dominates the dynamics of the system, leading to a disappearance of the oscillatory behavior. Although the dephasing rate is large (e.g., the red-dotted curve), the effect of the measurement on qubit-1 at time 0 can still be transited to qubit-3 via the coherent coupling between the qubits, making the ST SW gradually increase. For brevity, we are omitting analogous plots for the STS robustness.
Example 2: The spatio-temporal steering robustness in the Fenna-Matthews-Olson complex
Much attention has been devoted to the possible functional role of quantum coherence66, 67 in photosynthesis bacteria, since the observation of possible quantum coherent motion of an excitation within the FMO complex – a photosynthetic pigment-protein complex68,69,70. A simple treatment of the excitation transfer in the FMO complex normally considers seven coupled sites (chromophores), as shown in Fig. 3, and their interaction with the environment. The hierarchy method71,72,73,74,75 or other open-quantum system models76, 77 can be used to explain the presence of quantum coherence and predict the physical quantities observed in experiments.
(a) Schematic diagram of a single monomer of the FMO protein complex. This monomer contains eight sites (here we show only seven of them). In the bacterial photosynthesis, the excitation from the light-harvesting antenna enters the FMO complex at sites 6 or 1 and is then transferred from one site to another. The excitation can irreversibly jump to the reaction center, when it reaches site-3. In this work, the initial condition is set as site-6 in a mixed excited state while the other sites are in ground states. BChl stands for a bacteriochlorophyll molecule. (b) Schematics of how the monomer exists in a trimer, and acts as a wire connecting a large antenna complex to the reaction center.
Empowered by STS, one can ask the following questions for a network like the FMO protein complex: When an excitation arrives at site-6, and propagates through the network, how large is its quantum influence, if any, to other sites? When do such nonclassical correlations vanish? Previously, quantum entanglement in the FMO complex has been theoretically analyzed78. Given the fact that the excitation transfer is dynamic in nature, with a specific starting site (site-1 or site-6), it is more natural to examine the nonclassical correlation between sites at different times by using the STS measures. However, we point out that evaluating these measures requires measurements in different “excitation” bases at both source and target sites. Thus, evaluating these measures represents an analysis of the network itself, and how quantum correlations propagate through it, much akin to the approach taken in ref. 79.
The model Hamiltonian of the single FMO monomer containing N sites can be written as (see, e.g. ref. 80 and references therein):
where the state Pauli operators represent an electronic excitation at site n, (n \(\in \) 1, …, 7), such that \({\sigma }_{z}^{(n)}=|{e}^{(n)}\rangle \langle {e}^{(n)}|-|{g}^{(n)}\rangle \langle {g}^{(n)}|\), ε n is the site energy of chromophore n, and J n,n′ is the excitonic coupling between the nth and n′th sites. In the literature, because of the rapid recombination of multiple excitations in such a complex, it is common to simplify drastically this model by assuming that the whole complex only contains a single excitation. In that case the 27 dimensional Hilbert space is reduced to a 7 dimensional Hilbert space. Here, while we also assume only a single-excitation, we keep the full 27 dimensional Hilbert space to enable us to consider measurements in a basis which represent superpositions of excitations at various sites. (Note that for simplicity, we omit the recently discovered eighth site81).
In the regime that the excitonic coupling J n,n′ is large compared with the reorganization energy, the electron-nuclear coupling can be treated perturbatively82, and the open-system dynamics of the system can be described by the Haken-Strobl master-type equation83, 84,
where ρ is the system density matrix, and L[ρ] denotes the Lindblad operators
where the Lindblad superoperator L sink describes the irreversible excitation transfer from site-3 to the reaction center:
where \(s={\sigma }_{+}^{(R)}{\sigma }_{-}^{\mathrm{(3)}}\), with \({\sigma }_{+}^{(R)}\) representing the creation of an excitation in the reaction center, and Γ denotes the transfer rate. The other Lindblad superoperator, L deph, describes the temperature-dependent dephasing with the rate γ dp:
where \({A}_{n}={\sigma }_{z}^{(n)}\). This dephasing Lindblad operator leads to the exponential decay of the coherences between different sites in the system density matrix. The pure-dephasing rate γ dp can be estimated by applying the standard Born-Markov system-reservoir model85, 86. We assume an Ohmic spectral density, which, combined with the Born-Markov approximations, leads to a dephasing rate directly proportional to the temperature86. While more complex treatments are necessary to fully describe the true dynamics of the FMO complex, here we restrict ourselves to this weak-coupling Lindblad form for numerical efficiency and easier interpretation of results. Note that there exists a factor 1/8 between the dephasing rate γ dp here and the orthodox one in the 7-site model.
In the FMO monomer, the excitation transferring from site-3 to the reaction center takes place on a time scale of ~1 ps, and the dephasing occurs on a time scale of ~100 fs86. These two time scales are both much faster than that of the excitonic fluorescence relaxation (~1 ns), which is, thus, omitted here for simplicity. Here we present the values used for the system Hamiltonian in calculating the excitation transfer87:
Here the diagonal elements correspond to ε n , and the off-diagonals to J n,n′. We omit the large ground-state off-set, as it does not influence the results. This FMO dynamics description is based on our former work80.
In Fig. 4, we numerically calculated the STS robustness of site-6 to other sites by using the Haken-Strobl equation of motion80, 84. In plotting this figure, the temperature is chosen to be T = 15 K with the corresponding dephasing rate γ dp = 7.7 cm−1 and the decay rate (into the reaction center from site-3 only) Γ = 5.3 cm−1. As seen from this figure, the largest STS robustness occurs from site-6 to site-5. This is because site-6 and site-5 have the second largest intersite coupling (≈89.7 cm−1) in the whole network. Another interesting fact is that the robustness of site-6 to site-7 has the second largest magnitude (with a time delay) and the longest vanishing time (death time) of the STS robustness. In view of the coupling strength of the Hamiltonian, this may be due to the relative strong couplings of site-5 to site-4 (≈70.7 cm−1) and site-4 to site-7 (≈61.5 cm−1), such that the influence from site-6 is transferred through these sites with a time delay. In other words, the STS robustness not only gives the magnitude of the nonclassical correlations between two sites, but also gives the information of how long the nonclassical correlation takes to arrive, and how long it can be sustained.
Evolution of the STS robustness (ST SR) in the FMO complex. (a) The main figure together with the insets show the decays of the STS robustness of the assemblages \({\{{\sigma }_{a|x}^{{\rm{ST}}}(t)\}}_{a,x}\) of site-5 and site-7 respectively. (b) The black-dotted, red-dashed, blue-solid, and green dash-dotted curves are represent STS robustness of the assemblages \({\{{\sigma }_{a|x}^{{\rm{ST}}}(t)\}}_{a,x}\) of site-1, 2, 3, and 4 respectively. As the previous case, the measurement settings on site-6 at time 0 are the Pauli set X, Y, and Z. We assumed that the FMO is cooled down to T = 15 K, the FMO initial state is completely mixed at site-6 while the other sites are in ground state, the dephasing rate is 7.7 cm−1, and the decay rate is 5.3 cm−1. Again, for brevity, we do not present analogous plots for the STS weight.
Conclusions
Although the concept of spatio-temporal quantum entanglement is fundamentally difficult to be described consistently, we showed that STS, describing a certain type of spatio-temporal nonclassical correlations, can indeed be defined and quantified in an operational way. We hope that this may provide a wider view than the purely spatial or temporal correlations separately. In addition, we showed that STS, with its measures, including the STS weight and STS robustness, can be useful to assess nonclassical correlations in quantum networks or other open quantum systems. As an application, we described two examples of testing nonclassical correlations in a toy model of a three-qubit quantum network and in a more realistic model of the excitation transfer in the seven-site FMO complex. We believe that STS can be useful also for testing nonclassical correlations of more complex biological systems66, 79 and for describing quantum transport through artificial nano-structures88,89,90,91. Finally, we mention that a possible experimental demonstration of STS can be based on a delayed-time modified version of the experiment on temporal steering reported in ref. 47.
References
Schrödinger, E. Discussion of probability relations between separated systems. Math. Proc. Camb. Phil. Soc. 31, 555 (1935).
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Wiseman, H. M., Jones, S. J. & Doherty, A. C. Steering, entanglement, nonlocality, and the Einstein-Podolsky-Rosen paradox. Phys. Rev. Lett. 98, 140402 (2007).
Bell, J. S. On the Einstein-Podolsky-Rosen paradox. Physics 1, 195–200 (1964).
Brunner, N., Cavalcanti, D., Pironio, S., Scarani, V. & Wehner, S. Bell nonlocality. Rev. Mod. Phys. 86, 419–478 (2014).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865–942 (2009).
Reid, M. D. Demonstration of the Einstein-Podolsky-Rosen paradox using nondegenerate parametric amplification. Phys. Rev. A 40, 913–923 (1989).
Pusey, M. F. Negativity and steering: A stronger Peres conjecture. Phys. Rev. A 88, 032313 (2013).
Skrzypczyk, P., Navascués, M. & Cavalcanti, D. Quantifying Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 112, 180404 (2014).
Piani, M. & Watrous, J. Necessary and sufficient quantum information characterization of Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 114, 060404 (2015).
Cavalcanti, E. G., Jones, S. J., Wiseman, H. M. & Reid, M. D. Experimental criteria for steering and the Einstein-Podolsky-Rosen paradox. Phys. Rev. A 80, 032112 (2009).
Saunders, D. J., Jones, S. J., Wiseman, H. M. & Pryde, G. J. Experimental EPR-steering using Bell-local states. Nat. Phys. 6, 845–849 (2010).
Walborn, S. P., Salles, A., Gomes, R. M., Toscano, F. & Souto Ribeiro, P. H. Revealing hidden Einstein-Podolsky-Rosen nonlocality. Phys. Rev. Lett. 106, 130402 (2011).
Wittmann, B. et al. Loophole-free Einstein-Podolsky-Rosen experiment via quantum steering. New J. Phys. 14, 053030 (2012).
Smith, D. H. et al. Conclusive quantum steering with superconducting transition-edge sensors. Nat. Commun. 3, 625 (2012).
Bennet, A. J. et al. Arbitrarily loss-tolerant Einstein-Podolsky-Rosen steering allowing a demonstration over 1 km of optical fiber with no detection loophole. Phys. Rev. X 2, 031003 (2012).
Händchen, V. et al. Observation of one-way Einstein-Podolsky-Rosen steering. Nat. Photon. 6, 596–599 (2012).
Steinlechner, S., Bauchrowitz, J., Eberle, T. & Schnabel, R. Strong Einstein-Podolsky-Rosen steering with unconditional entangled states. Phys. Rev. A 87, 022104 (2013).
Su, H. Y., Chen, J. L., Wu, C., Deng, D. L. & Oh, C. H. Detecting Einstein-Podolsky-Rosen steering for continuous variable wavefunctions. I. J. Quant. Infor. 11, 1350019 (2013).
Schneeloch, J., Dixon, P. B., Howland, G. A., Broadbent, C. J. & Howell, J. C. Violation of continuous-variable Einstein-Podolsky-Rosen steering with discrete measurements. Phys. Rev. Lett. 110, 130407 (2013).
Gallego, R. & Aolita, L. Resource theory of steering. Phys. Rev. X 5, 041008 (2015).
Kogias, I., Lee, A. R., Ragy, S. & Adesso, G. Quantification of Gaussian quantum steering. Phys. Rev. Lett. 114, 060403 (2015).
Costa, A. C. S. & Angelo, R. M. Quantification of Einstein-Podolski-Rosen steering for two-qubit states. Phys. Rev. A 93, 020103 (2016).
Uola, R., Moroder, T. & Gühne, O. Joint measurability of generalized measurements implies classicality. Phys. Rev. Lett. 113, 160403 (2014).
Quintino, M. T., Vértesi, T. & Brunner, N. Joint measurability, Einstein-Podolsky-Rosen steering, and Bell nonlocality. Phys. Rev. Lett. 113, 160402 (2014).
Uola, R., Budroni, C., Gühne, O. & Pellonpää, J.-P. One-to-one mapping between steering and joint measurability problems. Phys. Rev. Lett. 115, 230402 (2015).
Cavalcanti, D. & Skrzypczyk, P. Quantitative relations between measurement incompatibility, quantum steering, and nonlocality. Phys. Rev. A 93, 052112 (2016).
Chen, S.-L., Budroni, C., Liang, Y.-C. & Chen, Y.-N. Natural framework for device-independent quantification of quantum steerability, measurement incompatibility, and self-testing. Phys. Rev. Lett. 116, 240401 (2016).
Li, C.-M., Chen, Y.-N., Lambert, N., Chiu, C.-Y. & Nori, F. Certifying single-system steering for quantum-information processing. Phys. Rev. A 92, 062310 (2015).
Li, C.-M. et al. Genuine high-order Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 115, 010402 (2015).
He, Q. & Reid, M. D. Genuine multipartite Einstein-Podolsky-Rosen steering. Phys. Rev. Lett. 111, 250403 (2013).
Cavalcanti, D. et al. Detection of entanglement in asymmetric quantum networks and multipartite quantum steering. Nat. Commun. 6, 7941 (2015).
Armstrong, S. et al. Multipartite Einstein-Podolsky-Rosen steering and genuine tripartite entanglement with optical networks. Nat. Phys. 11, 167–172 (2015).
Xiang, Y., Kogias, I., Adesso, G. & He, Q. Multipartite Gaussian steering: Monogamy constraints and quantum cryptography applications. Physical Review A 95, 10101 (2017).
The special issue of J. Opt. Soc. B on 80 years of steering and the Einstein–Podolsky–Rosen paradox. J. Opt. Soc. B 32, A1–A91 (2015).
Hanbury-Brown, R. & Twiss, R. Q. A test of a new type of stellar interferometer on sirius. Nature (London) 178, 1046–1048 (1956).
Glauber, R. J. Quantum Theory of Optical Coherence: Selected Papers and Lectures (Wiley-VCH, Weinheim, 2007).
Leifer, M. S. & Spekkens, R. W. Towards a formulation of quantum theory as a causally neutral theory of bayesian inference. Phys. Rev. A 88, 052130 (2013).
Fitzsimons, J. F., Jones, J. A. & Vedral, V. Quantum correlations which imply causation. Sci. Rep. 5, 18281 (2015).
Horsman, D., Heunen, C., Pusey, M. F., Barrett, J. & Spekkens, R. W. Can a quantum state over time resemble a quantum state at a single time? arxiv:1607.03637 (2016).
Chen, Y.-N. et al. Temporal steering inequality. Phys. Rev. A 89, 032112 (2014).
Karthik, H. S., Tej, J. P., Devi, A. R. U. & Rajagopal, A. K. Joint measurability and temporal steering. J. Opt. Soc. Am. B 32, A34–A39 (2015).
Mal, S., Majumdar, A. S. & Home, D. Probing hierarchy of temporal correlation requires either generalised measurement or nonunitary evolution. arxiv:1510.00625 (2016).
Chen, S.-L. et al. Quantifying non-Markovianity with temporal steering. Phys. Rev. Lett. 116, 020503 (2016).
Chiu, C.-Y., Lambert, N., Liao, T.-L., Nori, F. & Li, C.-M. No-cloning of quantum steering. NPJ Quantum Information 2, 16020 (2016).
Bartkiewicz, K., Černoch, A., Lemr, K., Miranowicz, A. & Nori, F. Temporal steering and security of quantum key distribution with mutually unbiased bases against individual attacks. Phys. Rev. A 93, 062345 (2016).
Bartkiewicz, K., Černoch, A., Lemr, K., Miranowicz, A. & Nori, F. Experimental temporal quantum steering. Scientific Reports 6, 38076 (2016).
Blankenship, R. E. Molecular Mechanism of Photosynthesis (Blackwell Science, London, 2002).
Christandl, M., Datta, N., Ekert, A. & Landahl, A. J. Perfect state transfer in quantum spin networks. Phys. Rev. Lett. 92, 187902 (2004).
Chakraborty, S., Novo, L., Ambainis, A. & Omar, Y. Spatial search by quantum walk is optimal for almost all graphs. Phys. Rev. Lett. 116, 100501 (2016).
Leggett, A. J. & Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 54, 857 (1985).
Fritz, T. Quantum correlations in the temporal Clauser-Horne-Shimony-Holt (CHSH) scenario. New J. Phys. 12, 083055 (2010).
Dressel, J., Broadbent, C. J., Howell, J. C. & Jordan, A. N. Experimental violation of two-party Leggett-Garg inequalities with semiweak measurements. Phys. Rev. Lett. 106, 040402 (2011).
Maroney, O. J. E. Detectability, invasiveness and the quantum three box paradox. arxiv:1207.3114 (2012).
Kofler, J. & Brukner, V. Condition for macroscopic realism beyond the Leggett-Garg inequalities. Phys. Rev. A 87, 052115 (2013).
Budroni, C., Moroder, T., Kleinmann, M. & Gühne, O. Bounding temporal quantum correlations. Phys. Rev. Lett. 111, 020403 (2013).
Emary, C., Lambert, N. & Nori, F. Leggett-Garg inequalities. Rep. Prog. Phys. 77, 016001 (2014).
Vandenberghe, L. & Boyd, S. Semidefinite programming. SIAM Review 38, 49 (1996).
Eisert, J. & Plenio, M. B. A comparison of entanglement measures. J. Mod. Opt. 46, 145 (1999).
Virmani, S. & Plenio, M. B. Ordering states with entanglement measures. Phys. Lett. 31, 268 (2000).
Miranowicz, A. & Grudka, A. Ordering two-qubit states with concurrence and negativity. Phys. Rev. A 70, 032326 (2004).
Bartkiewicz, K., Horst, B., Lemr, K. & Miranowicz, A. Entanglement estimation from Bell inequality violation. Phys. Rev. A 88, 052105 (2013).
Miranowicz, A. et al. Statistical mixtures of states can be more quantum than their superpositions: Comparison of nonclassicality measures for single-qubit states. Phys. Rev. A 91, 042309 (2015).
Ku, H.-Y. et al. In preparation (2016).
Delvenne, J.-C., Yaliraki, S. N. & Barahona, M. Stability of graph communities across time scales. Proc. Nat. Acad. Sc. 107, 12755 (2010).
Lambert, N. et al. Quantum biology. Nat. Phys. 9, 10 (2013).
Scholes, G. D., Fleming, G. R., Olaya-Castro, A. & van Grondelle, R. Lessons from nature about solar light harvesting. Nat. Chem. 3, 763–774 (2011).
Engel, G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature (London) 446, 782–786 (2007).
Collini, E. et al. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature (London) 463, 644–647 (2010).
Panitchayangkoon, G. et al. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. PNAS 107, 12766–12770 (2010).
Ishizaki, A. & Fleming, G. R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. PNAS 106, 17255–17260 (2009).
Ishizaki, A. & Fleming, G. R. Theoretical examination of quantum coherence in a photosynthetic system at physiological temperature. J. Chem. Phys. 130, 234111 (2009).
Ishizaki, A. & Tanimura, Y. Quantum dynamics of system strongly coupled to low-temperature colored noise bath: Reduced hierarchy equations approach. J. Phys. Soc. Jap. 74, 3131–3134 (2005).
Tanimura, Y. Nonperturbative expansion method for a quantum system coupled to a harmonic-oscillator bath. Phys. Rev. A 41, 6676–6687 (1990).
Tanimura, Y. & Kubo, R. Time evolution of a quantum system in contact with a nearly Gaussian-Markoffian noise bath. J. Phys. Soc. Jap. 58, 101–114 (1989).
Jang, S., Cheng, Y.-C., Reichman, D. R. & Eaves, J. D. Theory of coherent resonance energy transfer. J. Chem. Phys. 129, 101104 (2008).
Kolli, A., Nazir, A. & Olaya-Castro, A. Electronic excitation dynamics in multichromophoric systems described via a polaron-representation master equation. J. Chem. Phys. 135, 154112 (2011).
Sarovar, M., Ishizaki, A., Fleming, G. R. & Whaley, K. B. Quantum entanglement in photosynthetic light-harvesting complexes. Nat Phys 6, 462–467 (2010).
Faccin, M., Migdal, P., Johnson, T. H., Bergholm, V. & Biamonte, J. D. Community detection in quantum complex networks. Phys. Rev. X 4, 041012 (2014).
Chen, G.-Y., Lambert, N., Li, C.-M., Chen, Y.-N. & Nori, F. Rerouting excitation transfers in the Fenna-Matthews-Olson complex. Phys. Rev. E 88, 032120 (2013).
Olbrich, C. et al. From atomistic modeling to excitation transfer and two-dimensional spectra of the FMO light-harvesting complex. Journal of Physical Chemistry B 115, 8609–8621 (2011).
Ishizaki, A., Calhoun, T. R., Schlau-Cohen, G. S. & Fleming, G. R. Quantum coherence and its interplay with protein environments in photosynthetic electronic energy transfer. Physical Chemistry Chemical Physics 12, 7319 (2010).
Haken, H. & Strobl, Z. G. An exactly solvable model for coherent and incoherent exciton motion. Phys. 262, 35 (1973).
Quantum Effects in Biology, edited by Mohseni, M. et al. (Cambridge University Press, Cambridge, UK, 2014).
Breuer, H. P. & Petruccione, F. The Theory of Open Quantum Systems (Oxford University Press, Oxford, 2007).
Rebentrost, P., Mohseni, M., Kassal, I., Lloyd, S. & Aspuru-Guzik, A. Environment-assisted quantum transport. New Journal of Physics 11, 033003 (2009).
Adolphs, J. & Renger, T. How proteins trigger excitation energy transfer in the FMO complex of green sulfur bacteria. Biophysical Journal 91, 2778–2797 (2006).
Lambert, N., Emary, C., Chen, Y.-N. & Nori, F. Distinguishing quantum and classical transport through nanostructures. Phys. Rev. Lett. 105, 176801 (2010).
Emary, C., Lambert, N. & Nori, F. Leggett-Garg inequality in electron interferometers. Phys. Rev. B 86, 235447 (2012).
Lambert, N., Johansson, R. & Nori, F. Macrorealism inequality for optoelectromechanical systems. Phys. Rev. B 84, 245421 (2011).
Lambert, Neill, Debnath, Kamanasish, Kockum, AntonFrisk, Knee, GeorgeC., Munro, WilliamJ. & Nori, Franco Leggett-Garg inequality violations with a large ensemble of qubits. Phys. Rev. A 94, 012105 (2016).
Acknowledgements
The authors acknowledge fruitful discussions with Huan-Yu Ku and Karol Bartkiewicz. We acknowledge the support of a grant from the John Templeton Foundation. This work is supported partially by the National Center for Theoretical Sciences and Ministry of Science and Technology (MOST), Taiwan, grant number MOST 103-2112-M-006-017-MY4. S.L.C. acknowledges the support of the DAAD/MOST Sandwich Program 2016 No. 57261473. C.M.L. and G.Y.C. are supported by the Ministry of Science and Technology, Taiwan, under the Grants Numbers MOST 104-2112-M-006-016-MY3 and 105-2112-M-005-008-MY3, respectively. F.N. was also partially supported by the RIKEN iTHES Project, the MURI Center for Dynamic Magneto-Optics via the AFOSR award number FA9550-14-1-0040, the IMPACT program of JST, CREST, and a Grant-in-Aid for Scientific Research (A).
Author information
Authors and Affiliations
Contributions
Y.N.C., N.L., C.M.L., and A.M. conceived the idea. S.L.C. carried out the calculations under the guidance of Y.N.C. and G.Y.C. All authors contributed to the interpretation of the work and the writing of the manuscript.
Corresponding author
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, SL., Lambert, N., Li, CM. et al. Spatio-Temporal Steering for Testing Nonclassical Correlations in Quantum Networks. Sci Rep 7, 3728 (2017). https://doi.org/10.1038/s41598-017-03789-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-03789-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.