Abstract
Multi-principle element alloys have enormous potential, but their exploration suffers from the tremendously large range of configurations. In the last decade such alloys have been designed with a focus on random solid solutions. Here we apply an experimentally verified, combined thermodynamic and first-principles design strategy to reverse the traditional approach and to generate a new type of hcp Al-Hf-Sc-Ti-Zr high entropy alloy with a hitherto unique structure. A phase diagram analysis narrows down the large compositional space to a well-defined set of candidates. First-principles calculations demonstrate the energetic preference of an ordered superstructure over the competing disordered solid solutions. The chief ingredient is the Al concentration, which can be tuned to achieve a D019 ordering on the hexagonal lattice. The computationally designed D019 superstructure is experimentally confirmed by transmission electron microscopy and X-ray studies. Our scheme enables the exploration of a new class of high entropy alloys.
Similar content being viewed by others
Introduction
Alloy design by combining multiple elements in near-equimolar ratios has the potential of creating new, unique engineering materials, commonly known as high entropy alloys (HEAs) or multi-principal element alloys1,2,3,4,5. HEAs have been shown to have excellent mechanical properties6,7,8,9,10,11,12, as well as interesting magnetic13,14,15,16 and electronic properties17, 18. In contrast to conventional alloys, HEAs contain typically five or more elements19,20,21,22 with concentrations ranging from 5 to 35 at.%1. The original idea behind this concept is to maximize the configurational entropy to achieve a single phase disordered solid solution. Such concentrated disordered solutions have been shown to exist on the face-centered cubic (fcc) and body-centered cubic (bcc) lattice1,2,3, and more recently also on the hexagonal close-packed (hcp) lattice23,24,25,26. Theoretical approaches based on first principles were proposed27, 28 to replace the earlier empirical rules and to guide the search for disordered solid solutions.
Here we propose a reverse design strategy, with the aim of finding ordered structures in HEAs. This is motivated by the fact that—in contrast to fully disordered alloys—the ordered counterparts usually work-harden faster showing an improvement in their mechanical properties29, 30. The increased work-hardening rate of ordered alloys originates from a high storage rate of dislocations coupled with a general lack of dynamic recovery processes30. A prominent example of an outstanding impact of ordered phases leading to ultra-high strength are Ti3Al-base alloys31. In HEAs, ordered phases have been reported in bcc and fcc structures containing elements with a large electronegativity difference such as Al and Ni32,33,34,35,36. For example, increasing the Al concentration of fcc/bcc based Al x CoCrCuFeNi alloys leads to chemical ordering, which correlates with an increase in hardness1, although ductility and fracture toughness suffer typically37. Short range order has been reported in bcc and fcc HEAs38,39,40, but is difficult to address experimentally and remains a subject of debates. Ordered hcp based phases in HEAs have not been found so far. Such a new class of ordered hcp HEAs could potentially open new routes to improving materials properties, as may be anticipated from the beneficial properties of the hcp based “Super-Alpha-2” Ti3Al-base alloys31.
A note is due here. With an ordered HEA we do not mean that all elements occupy own sublattices as is typically the case in binary alloys. In HEAs, several elements can share the same sublattice with a preference of some of the elements to a specific sublattice, e.g., A and B atoms may occupy, say, the α-sublattice and C, D, and E atoms reside on the β-sublattice in an ordered ABCDE HEA. Or, just one atomic species could reveal a preference to a given sublattice whereas all other atoms may be equally distributed. As this comment should make clear, a large number of potential types of ordering is possible in HEAs, thereby opening new perspectives for alloy optimization and development.
The immense combinatorial amount of possible types of ordering and phases is, however, a fundamental challenge in developing multi-principle element alloys. To overcome this challenge, sophisticated approaches and design principles are required41, 42, which also need to go beyond presently employed ideas43. In this work we demonstrate how a combination of thermodynamic arguments, first principles calculations, and experiments can be used to narrow down the a priori large range of potential candidate structures and to find a material with the desired property. We stress that the combination of these different approaches is crucial for our purpose, as each of them, considered separately has certain limitations. We apply this strategy to the Al-Hf-Sc-Ti-Zr system with the goal of finding a new HEA with an ordered D019 superstructure on the hcp lattice.
Results
Thermodynamic analysis
In an ideal case, to find the desired ordered hcp superstructure for our Al-Hf-Sc-Ti-Zr HEA, we would perform a quantitative, CALPHAD44, 45 based stability analysis of the relevant phases. Unfortunately, CALPHAD parametrizations of multi-principal element alloys, as the considered five-component HEA, are unavailable as yet. This is nowadays a typical restriction for the design of HEAs. Moreover, even if a parametrization was available, it could not be guaranteed that it provides a reasonable description of the HEA system for which it has (in the usual case) not been optimized. We therefore employ the CALPHAD approach only in a qualitative manner, which nevertheless turns out to be a very powerful strategy to narrow down the candidates for the ab initio simulations. We employ in particular a strategically useful representation and analysis of the sub-binary phase diagrams of our system. The advantage is that all of these phase diagrams are determined experimentally and can be straightforwardly obtained from databases.
As shown in Fig. 1, except for the Al-containing binaries (top row) the other phase diagrams reveal a large solubility in the disordered bcc A2 phase (red regions) at higher temperatures, and mostly also in the disordered hcp A3 phase (light green) at lower temperatures. The good miscibility can be understood by considering the similar nature of the involved d transition elements, like the atomic volume or the electronegativity (Table 1). A closer look at Table 1 reveals, however, that Ti is somewhat special, having a smaller atomic volume and a larger electronegativity than Sc, Hf, and Zr. The special character of Ti is also reflected by the binary phase diagrams of the d elements (Fig. 1 without the top row), which show, e.g., that the Sc-Ti system features a miscibility gap in the hcp A3 phase, decomposing into a hcp A3 + hcp A3 two-phase field. The Hf-Ti system also shows a tendency to an hcp A3 + hcp A3 decomposition at lower temperatures, and in fact this applies also to the Ti-Zr system below the shown 400 K.
Phase diagrams of all 10 individual constituting binaries of the considered Al-Hf-Sc-Ti-Zr HEA. The phase diagrams for Hf-Ti, Hf-Zr, and Ti-Zr are based on the SGTE (2014) alloy database. The phase diagrams for Al-Hf, Al-Sc, Al-Zr, Sc-Ti, and Sc-Zr are based on the PanSolution database (ipandat.computherm.com). The Al-Ti phase diagram corresponds to the reassessment of Schuster and Palm69. The Sc-Hf phase diagram has been taken from ref. 70. and extended to temperatures below 1200 K by a hcp A3 single phase field.
Adding Al to the d transition elements changes the appearance of the binary phase diagrams completely (top row of Fig. 1). Al is a strong intermetallic former as is clearly reflected by its phase diagrams showing various intermetallic phases (grey regions). All of the Al phase diagrams show for example an Al3M phase (M = Hf, Sc, Ti, Zr) which forms a two-phase field with the fcc A1 phase towards the Al-rich side of the phase diagrams (grey-orange stripes). Almost all of the formed intermetallic phases are stoichiometric phases, i.e., they exist only at a single, fixed composition and have no solubility. The Al-Ti diagram is an exception. The L10 phase which forms at around Al50:Ti50 on an fcc lattice has an appreciable solubility range. The other, very special and for the present analysis important phase is the ordered D019 phase (dark green region) which forms at around Al25:Ti75 on the hcp lattice. It has a similarly large solubility range as the L10 phase, extending towards both, the Al-rich and Ti-rich side. The D019 phase is embedded into an hcp A3 solid solution (light green region), which extends even to a composition of 50:50 at higher temperatures. This solubility range is much larger than for any of the other shown Al phase diagrams, again indicating the special character of Ti among the investigated d elements. Table 1 shows that the atomic volume and electronegativity of Ti are indeed closer to the ones of Al than to the ones of the other d elements.
In order to elucidate (at least qualitatively) how the binary information can be extended to the five-component Al-Hf-Sc-Ti-Zr HEA, we combined the binary diagrams into a 3D-representation as shown in Fig. 2. Joining all diagrams from Fig. 1 is not feasible and we therefore restricted the diagram to a quaternary sub-diagram, keeping the most relevant elements for our purpose, Al (at the top) and Ti (to the left). An important feature that we have added to the 3D-phase diagram is the AlM3 plane where M = Ti, Sc, Hf, Zr. Moving on this plane towards the Ti-Al phase diagram we approach the D019 phase. Given this representation and the fact that—despite the discussed differences—Ti does feature chemical similarity with the other d elements, one can speculate that the ordered D019 phase extends into the multi-component system as indicated by the dark green arrow in Fig. 2.
3D representation of the multi-component phase diagram constructed from the binary diagrams (Fig. 1). For visualization purposes, the Zr-binary phase diagrams (similar to the ones of Hf, see Fig. 1) are not shown. Black filled circles indicate the phase diagram trajectory for varying Al-concentration including the including the main alloy for the ab initio and experimental investigations with 15 at.% Al.
In ref. 46. the equiatomic HfScTiZr multi-principle element alloy was studied and it was shown that it consists of a disordered hcp A3 solid solution. Taking this alloy as a reference (black dot labeled “0 Al” in Fig. 2) and introducing Al into this system with a concentration of >5 at.%, allows us to stay within the usual definition of HEAs. The only design criterion left is which element(s) to remove for Al. From the above analysis we know that Ti is a critical factor for the formation of the D019 phase and we thus keep its concentration. Out of the remaining d elements Sc shows the largest tendency to phase decomposition (Sc-Ti phase diagram), which is related to the large atomic radius and electronegativity of Sc (Table 1). This special feature of Sc was responsible for the presence of Sc enriched phases and a strong segregation of Ti to interfaces in HfScTiZr46. We therefore substitute in the subsequent computational modeling Sc by Al, in particular taking concentration steps of 5 at.% Al (black points “5 Al”, “10 Al”, and “15 Al” in Fig. 2), approaching thereby the AlM3 plane and thus the possibility of D019 ordering.
Ab initio calculations of the phase stabilities
In order to quantitatively assess the phase stabilities for the selected compositions, we resort in the following to unbiased and very accurate, parameter-free first-principles calculations realized by DFT. In particular we investigate whether an ordered D019 superstructure can be energetically stable over the fully disordered hcp A3 and bcc A2 solid solutions, which are the most relevant phases according to the above phase diagram analysis. Phase decomposition could be in principle also investigated but is very difficult in practice due to the large configuration space. Therefore, our computations were restricted to energy differences at fixed compositions. We stress that with this approximation of a fixed composition, we have no information about potentially stable phases at other compositions. Within our general, combined strategy, the quality of this approximation can be only assessed a posteriori by comparison to the experimental results.
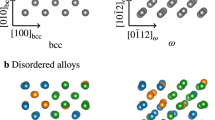
Within the fixed composition approximation, the D019 and A3 phase are located on the same hcp lattice, the difference between them being related to the chemical order/disorder. To resemble this situation as closely as possible we have generated large special quasi random structures (SQS). Figure 3a and b show the SQS supercell representing the hcp A3 phase with full chemical disorder. Figure 3c and d show the supercell representing the D019 phase. The D019 like supercell requires a close look to understand where the ordering occurs. Note for that purpose the small red balls attached to some of the atoms in Fig. 3c and d, which indicate the sublattice positions of the Al atoms if the composition was strictly AlM3 (M = Ti, Sc, Hf, Zr). For our selected compositions, there are not enough Al atoms to fill up all these sublattice sites, and thus this sublattice is only partially ordered. The remaining sites of the Al sublattice must be filled up by the other constituents and we have assumed that all other atoms can enter the Al sublattice and that there is no ordering among them. The other sublattice contains the d elements only and is fully disordered. To guarantee convergence with respect to chemical disorder we tested two distinct SQS supercells for each of the phases, and to match the experimental boundary conditions we optimized the volume, c/a ratio, and atomic relaxations (to fully include local lattice distortions47) for D019, hcp A3, and bcc A2 separately.
Side and bottom view of the 216-atom super cells of the disordered hcp A3 structure [(a) and (b)] as well as for the partially ordered D019 structure [(c) and (d)] employed in the first-principles calculations for Al15Hf25Sc10Ti25Zr25 at.%. The small red dots in (c) and (d) indicate the sublattice positions for the ordered Al atoms in the D019 superstructure.
The resulting ab initio energetics for the example of Al15Hf25Sc10Ti25Zr25 at.% is summarized in Fig. 4. Figure 4a shows the energy contour plot for the D019 phase as a function of atomic volume and c/a ratio. The two main conclusions are: (1) The energy dependence on the c/a ratio is small. In the investigated c/a range (1.57…1.63) the energy at the equilibrium volume changes only by 2 meV/atom. (2) The equilibrium c/a ratio and the equilibrium volume are independent of each other. For example, for all volumes the equilibrium c/a ratio is 1.60 as indicated by the black dashed line. Both conclusions apply likewise to the hcp A3 phase, except for the fact that the equilibrium c/a ratio is slightly smaller with 1.59 (red dashed line). Table 2 shows that the computed values agree well with our experimental results. Figure 4b compares the T = 0 K energies of all investigated phases revealing clearly that the D019 phase is the most stable one. The variation in the energy difference due to the different SQS supercells for D019 and hcp A3 is reasonably small and we can conclude that the partially ordered D019 superstructure is about 30 meV/atom more stable than the fully disordered hcp A3 structure and about 60 meV/atom more stable than the disordered bcc A2 at T = 0 K.
Ab initio energetics of the hcp based phases D019 and A3, and of the bcc based A2 phase for the Al15Hf25Sc10Ti25Zr25 at.% HEA. (a) Energy contour plot at T = 0 K for the D019 phase as a function of volume and c/a ratio. The bold black numbers give the value of the contours in meV/atom. The black dashed line indicates the equilibrium c/a ratio (of SQS 1) and the black and white crosses mark the equilibrium volumes of the two employed supercells (SQS 1 and 2). The red solid line shows the 1 meV/atom contour of the hcp A3 energy surface. The red dashed line indicates the equilibrium c/a ratio for hcp A3 and the red cross the corresponding equilibrium volume. (b) T = 0 K energy-volume curves for D019 and A3 (with two SQS’ for each phase) at the equilibrium c/a ratios as indicated by the dashed lines in (a). The energy-volume curve of bcc A2 which has been obtained by an average over the two studied SQS supercells (see the Methods section on the ab initio energetics) is also shown. (c) Difference in the Gibbs energies of D019 and A3 as a function of temperature (D019 corresponding to the zero line). The Gibbs energy difference is decomposed into the T = 0 K energy (0 K), the vibrational (vib), electronic (el), and configurational (conf) contribution. The final curve corresponds to the blue solid line, resulting in a transition temperature of 1230 K as indicated by the vertical dashed line. The dotted line shows the difference between the Gibbs energy of D019 and bcc A2 containing all contributions. The onset of melting as obtained from our experimental results is indicated by the black arrow.
In order to determine the temperature dependent phase stabilities, we computed finite temperature contributions due to electrons, atomic vibrations, and configurational entropy. The electronic and vibrational Gibbs energies are similar for all three phases and contribute therefore little to the differences as exemplified by the small light gray and light green shaded areas in Fig. 4c for D019 vs. A3. A similar observation was recently made for other HEAs48. The dominant contribution to the Gibbs energy difference comes from the configurational entropy (blue shaded area). The reason is that the configurational entropy is considerably smaller for the D019 phase, because the Al atoms are confined to the Al sublattice in contrast to the hcp A3 phase where the Al atoms can be located on any of the hcp lattice sites. Therefore, the stability of the disordered hcp A3 phase is more and more increased as temperature rises, leading eventually to a phase transition from D019 to A3. Averaging over both SQS supercells for each phase gives a transition temperature of about 1230 K. Note that by assuming an ideal entropy [Eqs (5–11)] and neglecting short-range order, the predicted order-disorder temperature is likely underestimated48, 49. Considering the variation in the energies of the SQS supercells (Fig. 4b) provides in fact a temperature window of 1100…1350 K for a possible transition as indicated by the gray diagonal stripes in Fig. 4c. The stability of the bcc A2 is likewise increased as compared to D019, but—due to the considerable T = 0 K offset—bcc A2 cannot compete with the other phases at any of the investigated temperatures.
Reducing the Al concentration (black dots in Fig. 2) causes a decrease of the order-disorder transition temperature, as already anticipated based on the phase diagram analysis. This decrease is, however, not very strong. For Al5Hf25Sc20Ti25Zr25 at.% the transition temperature is reduced only by about 200 K to 1000 K. The reason for the rather weak reduction of the order-disorder transition temperature is found in the detailed balance between the T = 0 K energy and the thermal entropy difference. The T = 0 K energy difference between the partially ordered D019 superstructure and the disordered hcp A3 phase is indeed considerably smaller for the Al5Hf25Sc20Ti25Zr25 at.% composition (Al5: +6 meV/atom vs. Al15: +30 meV/atom). But, the difference in the configurational entropy likewise decreases because the Al5Hf25Sc20Ti25Zr25 alloy has even less order and thus more configurational disorder than the Al15Hf25Sc10Ti25Zr25 one.
Microstructure characterization
Based on the preceding theoretical analysis we have selected the composition of Al15Hf25Sc10Ti25Zr25 at.% for a detailed experimental investigation. The SEM image of the corresponding as cast sample (Fig. 5a) indicates a two-phase microstructure with a fine plate arrangement, consisting of laths with a bimodal size distribution: coarse laths with 2–30 μm in length and 0.3–0.8 μm in thickness, and fine laths of 0.5–4 μm in length and 0.01–0.3 μm in thickness, and areas of a second phase between the laths (the interspace region with dark contrast). This microstructure morphology is similar to the α‘ martensitic one in rapidly cooled Ti-6Al-4V wt.% alloys31.
Microstructure of the Al15Hf25Sc10Ti25Zr25 at.% HEA in the as-cast state; (a) SEM image, (b) TEM-BF with SAED patterns and EDS point analysis taken at the red squares, with the results given in Table 3.
The TEM bright field image in Fig. 5b shows contrast from a few large laths (bright regions) with a thickness of 0.3–0.5 μm into which smaller laths of 20–100 nm in size are embedded. The concentrations shown in Table 3 (obtained from TEM-EDS) indicate a rather homogenous distribution of the involved elements in the matrix with small segregation of Al to the interspace region. This small concentration variation suggests the presence of two types of phases, consistent with the SEM results (Fig. 5a).
The X-ray analysis of the as cast alloy (lower panel in Fig. 6) indicates—except for a small amount of a primary (Sc,Zr)2Al phase with hexagonal structure—the presence of a hexagonal solid solution with lattice constants of a = 3.1092 Å and c = 4.9271 Å (see also Table 2) and space group P6 3 /mmc. The SAED pattern shown in the inset of Fig. 5b is consistent with the X-ray results, showing strong reflections at the standard hcp positions of (2021) and (02–22). However, a closer inspection of the SAED pattern also shows an additional weak reflection at (01–11) and (21–30) (highlighted by the circles in the inset of Fig. 5b), which is an indication of the onset of ordering on the hcp lattice. Since the X-ray analysis does not indicate any ordering, we conclude that the partial ordering in the as cast state is weak and can be only detected by the more sensitive SAED method.
In order to determine the effect of temperature on the microstructure of the Al15Hf25Sc10Ti25Zr25 HEA, a DTA analysis was conducted (Fig. 7). The first heating curve of the as-cast sample (black line) reveals several small exothermal peaks below 800 °C (cf. zoom in the inset) related to the transition from the meta-stable as-cast state towards the equilibrium state. A larger endothermal peak is present at around 950 °C presumably caused by dissolution of the (Sc,Zr)2Al precipitates. The two weak, exothermal peaks below 800 °C completely vanished after the first heating and cooling cycle. Similarly, the peak around 950 °C continuously became smaller and vanished after some heating/cooling cycles indicating that the (Sc,Zr)2Al precipitates were meta-stable. The red line in Fig. 7 shows the heating curve after six times heating and cooling, where no more changes occurred in the curves indicating that the material was in an equilibrated state. A new endothermal peak is visible near 900 °C. We identify this peak as corresponding to the order-disorder transition from the partially ordered D019 superstructure to the disordered hcp A3 phase predicted by our ab initio calculations. The large peak at around 1500 °C corresponds to the melting transition [solidus = 1442(±2)°C and liquidus = 1500(±5)°C]. Since neither our calculations have predicted the disordered bcc A2 phase to be stable nor does our DTA curve show another peak before melting, we conclude that our HEA melts directly from the hcp A3 phase. Based on the knowledge of the DTA results we conducted an annealing of the as-cast sample at 1000 °C for 5 h, leading to plate coarsening of the solid solution (average size of the laths reached tens of microns), as well as to further homogenization of the chemical composition.
DTA heat flow curves of the Al15Hf25Sc10Ti25Zr25 at.% HEA. The black curve corresponds to the 1st heating cycle directly after casting. The red curve shows the 7th heating cycle which corresponds to the equilibrated situation, i.e., further heating cycles show the same dependence. The inset enlarges the 1st heating curve and the gray dashed line is a guide to the eye indicating the baseline.
The EBSD analysis of the lattice misorientations in the annealed sample revealed that a large fraction of grain boundaries is characterized by 60° and 90° misorientations, which constituted, respectively, 61% and 7% of the total boundary length (marked as black and white lines, respectively, in Fig. 8a). Additionally, Σ19 boundaries were also identified in the analyzed material. These results indicate that during annealing new grains, which maintain crystallographic orientation relationships, are nucleating at the edges of the existing grains. Subsequently, the microstructure coarsening proceeds through grain growth. In addition to the coarsening, we further identified small Sc, Zr enriched secondary precipitation particles with an irregular shape and 0.1–1.5 μm in size based on the EBSD map (small dark area, in Fig. 8a) and the electron diffraction results.
(a) Inverse Pole Figure (IPF) map after annealing, (b) TEM bright field images with SAED patterns and points of EDS analysis after annealing (cf. Table 3).
The TEM-BF image of the annealed sample (Fig. 8b) shows a large lath with strong D019 superstructure reflections (SAED pattern in the inset) and small precipitates of the Sc enriched phase. A volume ordering effect in the annealed sample was confirmed by X-ray analysis, where additional peaks in the range of low 2θ values were identified (marked with a circle in Fig. 6). Significant differences between peak intensities were observed (100, 002, 101 – A3 and 200, 002, 201 – D019). This suggests that the annealing led to a rearrangement of the atoms in the lattice. Additionally, small shifts of characteristic peaks to lower 2θ values were observed due to homogenization of the structure and dissolution of the (Sc,Zr)2Al precipitates (identified before in the as cast alloy and confirmed by the DTA analysis), which partially expanded the lattice.
Mechanical properties
The average hardness of the Al15Hf25Sc10Ti25Zr25 HEA in the as cast state was 524 HV and it decreased after annealing to 407 HV. This decrease is probably related to the coarsening of the microstructure and the strain release in the annealed sample. Compressive stress-strain plots corresponding to room temperature are shown in Fig. 9a for the as-cast state (curve 1) and after annealing at 1000 °C/5 h (curve 2). In the as-cast state, the sample shows a high yield strength of 1450 MPa and a high compression strength of 1950 MPa at a strain of 4.6%, fracturing in a brittle manner. Annealing decreases the yield strength down to 980 MPa and increases the compressive strength, even up to 2200 MPa at an appreciable strain level of 21.5%.
(a) Compression curves of the Al15Hf25Sc10Ti25Zr25 at.% alloy in the as cast state (curve 1) and annealed state at 1000 °C for 5 h (curve 2), and of Hf25Sc25Ti25Zr25 at.% in the as cast (curve 3) and annealed (curve 4) state. (b) TEM bright field image with SAED pattern of the annealed Al15Hf25Sc10Ti25Zr25 at.% HEA after compression to 22% strain.
The bright field TEM micrograph of the alloy after compressive deformation to about 22% plastic strain exhibits multiple shear bands of 50 to 100 nm thickness, with a high defect density (Fig. 9b). The SAED pattern, taken from a shear band region, shows reflections of the hexagonal superstructure with [1–100] zone axis. These observations confirm that the movement of dislocations and shear band formation represents the key mechanism of deformation in the Al15Hf25Sc10Ti25Zr25 HEA. In contrast, the dominant deformation mechanism of pure hcp based Mg, Ti, and Zr materials involves twinning rather than slip. It is known that slip leads to high local stress concentrations, causing an increase in hardness50,51,52. We believe that the shear band deformation is responsible for the high compressive plasticity of our ordered HEA with hexagonal superstructure. Additionally, the compressive strength of the chemically disordered Hf25Sc25Ti25Zr25 HEA was measured for comparison. It can be seen that adding aluminum to the Hf-Sc-Ti-Zr system increases the yield and compression strength, and ductility. The present Al15Hf25Sc10Ti25Zr25 HEA has also a higher compression strength and ductility than the ordered Ti3Al D019 phase at room temperature, showing values of 1050 MPa and 17.5%, respectively53.
In typical alloys an ordered structure leads to an increase in hardness and a decrease in ductility, see e.g. ref. 37. For example Ti-Al alloys with non-symmetrical (tetragonal) D022 crystal structure and with the D019-type Ti3Al phase are hard and brittle due to an insufficient number of independent slip systems for plastic deformation54. The situation is reversed in the present partially ordered hexagonal HEA, where compressive plasticity increases significantly with slight increases in yield strength. A higher strength and higher ductility were also observed in a Ti-Al system alloyed with Nb55. At present, we can only speculate that a possible reason for the unusual compressive properties of the ordered structure in the present HEA could be the increased number of elements in the system, leading to a plasticity and strength increase due to the reduced slip planarity and an increased non-basal slip activity, unlike in Ti3Al55. While further studies are required to clarify this point, our findings underline that conclusions on ordering in alloys derived from mechanical properties, in particular for HEAs, need to be carefully validated.
In order to evaluate to what extent these conclusions can be transferred to tensile deformation, we performed micro-mechanical tensile tests using a custom-built device56. Dog-bone shaped samples with a gauge length of about 3 mm and 1.0 × 0.3 mm2 cross section were cut by spark erosion from the as-cast and annealed Al15Hf25Sc10Ti25Zr25 HEAs. The results of the tensile tests at ambient conditions are shown in the supplementary material. Whereas a tensile elongation of about 0.5% (excluding the elastic part) was observed for the as-cast sample, the annealed sample broke in the elastic region at a stress of about 1000 MPa. Correspondingly, fundamentally different fracture surfaces were observed in these two states, namely a predominantly ductile fracture with a combination of transgranular and intergranular cracks in the as-cast state, and an explicitly transgranular brittle fracture in the annealed sample.
Nevertheless we can state that already 0.5% of tensile ductility at room temperature in the as-cast state is a highlight for an hcp-based HEA in view of the practical absence of similar studies, e.g., for α2-titanium aluminides. The partially ordered Al15Hf25Sc10Ti25Zr25 HEA with distinct sublattices does not reveal an enhanced tensile ductility and broke in brittle manner. However, the fracture surface reveals traces of significant dislocation activity. One has to be as well aware of the fact that second-phase particles [e.g., (Sc,Zr)2Al] may potentially limit the tensile ductility of the specimen.
These findings support our idea of a potential application of ordered HEAs as, e.g., strengthening particles in a hcp matrix.
Discussion
The original design strategy of multi-component high entropy alloys forming disordered random solid solutions is reversed. In contrast to the traditional scheme we specifically design ordered or partially ordered HEA superstructures. This is achieved by combining thermodynamic CALPHAD and ab initio calculations. A CALPHAD approach is employed to narrow down the large configuration space to a distinct series of Al-Hf-Sc-Ti-Zr alloys. Subsequent quantitative ab initio calculations demonstrate that the presence of aluminum in the Al15Hf25Sc10Ti25Zr25 at.% high entropy alloy can lead to the formation of a partially ordered D019-type hexagonal superstructure. The computationally predicted target compositions are experimentally verified. The microstructure of our alloy shows thermal stability during annealing at 1000 °C/5 h. In contrast to typical ordered alloys our compression strength studies revealed that the ordered hexagonal superstructure has high compressive ductility. In tension, we found a lack of ductility. It is important to stress that single phase titanium aluminides are usually characterized by an absence or significantly reduced tensile ductility at room temperature57 and the value of 0.5% tensile elongation to fracture in the present as-cast HEA is remarkable. We expect that the full potential of the discovered ordered HEA phase could be exploited in the future by optimizing its microstructure towards a combination of two phases (e.g., by adding Nb), a typical design strategy in α2-titanium aluminides31.
A strong impact of aluminum on high entropy alloys with hexagonal structure, with the possibility of superstructure formation, has been demonstrated. Our approach is general and can be used to design new HEAs with other types of ordered superstructures. Moreover we open the route to a new and hitherto unexplored class of ordered hcp HEAs, of which traditional counterparts are already well established and highly successfully applied in industrial applications.
Methods
First principles
We employed first-principles calculations within density-functional theory (DFT) as implemented in the VASP software58, 59 in conjunction with the projector-augmented wave method60 and the generalized gradient approximation in the Perdew-Burke-Ernzerhof parametrization61. A plane wave cutoff of 240 eV was chosen for all calculations. Chemical disorder was simulated by special quasi random structures (SQS)62. For both of the studied hcp phases, D019 and A3, 216 atom supercells were employed, corresponding to 6 × 6 × 3 times the primitive hcp cell. For both phases two distinct SQS structures were tested to assess the performance in representing the chemical disorder. Dense k-point grids of up to 5 × 5 × 5 were studied (27,000 k-point•atom) to ensure high numerical precision. The volume and c/a ratio of the supercells were optimized by computing total energies for a grid of 4 different c/a ratios (1.57, 1.59, 1.61, 1.63) for each of the 9 considered volumes chosen around the equilibrium volume. The 216 atom supercells contained 32 Al, 54 Hf, 22 Sc, 54 Ti, and 54 Zr atoms which well resembles the experimentally investigated Al15Hf25Sc10Ti25Zr25 alloy. The Al5Hf25Sc20Ti25Zr25 HEA was also represented with a 216 atom SQS supercell, but containing the following numbers of atoms: 11 Al, 54 Hf, 43 Sc, 54 Ti, and 54 Zr. The bcc A2 phase was investigated only for the Al15Hf25Sc10Ti25Zr25 HEA. We used a 54 atom supercell corresponding to 3 × 3 × 3 times the conventional cubic unit cell. The k-point mesh was set to 6 × 6 × 6. The volume was sampled on 8 points around the equilibrium volume. Since in the chosen 54 atom bcc supercell the exact composition of the hcp supercells cannot be achieved, we used the following trick. We created two bcc SQS supercells with slightly varying compositions, such that the average over them gave the exact hcp composition (for the Al15Hf25Sc10Ti25Zr25 HEA). In particular, one bcc SQS contained 8 Al, 13 Hf, 6 Sc, 13 Ti, and 14 Zr atoms, whereas the other one contained 8 Al, 14 Hf, 5 Sc, 14 Ti, and 13 Zr atoms. All T = 0 K calculations were performed with the Methfessel-Paxton technique63 with a smearing value of 0.1 eV. The energy volume dependence was fitted to a Vinet equation of state64.
In order to capture the effect of electronic excitations we employed the finite temperature extension to DFT by Mermin65. In particular, we computed the electronic free energy by66, 67
where T is the temperature, D(ε) the electronic density of states, f = f(ε,T) the Fermi-Dirac function, ε F the Fermi energy, and k B the Boltzmann constant. Atomic vibrations were treated within the Debye formalism as described in detail in ref. 68. For the configurational entropy we assumed ideal mixing. In this approximation, the configurational entropy of the fully disordered bcc A2 and hcp A3 phase is given by
where the x i are the element concentrations in the homogenously disordered alloy for the 5 different species i. For the partially ordered D019 phase, the configurational entropy can be decomposed into contributions for the two inequivalent sites A and B as
with
where the partial Al ordering results in two inequivalent sublattice concentrations of
determined by weighting factors \({w}_{i}^{A,B}\). The sublattice concentrations render the multiplicities of the sublattice of 1 and 3 as
fulfilling the sum rule, i.e., \(\sum _{i}{y}_{i}^{A,B}=1\). If Al is confined to the A-sublattice, \({w}_{{\rm{Al}}}^{A}=4\) and \({w}_{{\rm{Al}}}^{B}=0\), and assuming a homogenous distribution of the other elements (Hf, Sc, Ti, Zr), the weighting factors for the other four components are given by
and
Eqs (5–11) provide the ideal configurational entropy of bcc A2, hcp A3, and D019 for any given composition x i . The assumption of ideal configurational entropy (of mixing) results by definition in 1st order phase transitions and typically provides theoretical lower bounds of order-disorder transition temperatures48, 49.
Experimental
Our experimental analysis focused mainly on the composition of Al15Hf25Sc10Ti25Zr25 at.% which shows the superstructure. An additional alloy with a composition of Al5Hf25Sc20Ti25Zr25 at.% was prepared and analyzed to confirm that it contains no superstructure. The alloys were prepared from elements of 99.99 wt.% purity in an arc melting furnace with a water-cooled copper plate under a protective Ar atmosphere. For structural characterization, cross sections of drops were analyzed. The drops solidified with an average cooling rate of 300 °C/s. X-ray measurements of the phase composition were performed using a Philips PW 1410 diffractometer and CoKα filtered radiation. Scans were performed on polished cross sectioned samples at 15° to 100°, with a step size of 0.02°, and a dwell time of 10 s. A Rietveld refinement was performed in order to determine the type of structure and lattice parameters. The microstructure was examined using a scanning electron microscope (SEM), FEI Quanta equipped with an energy-dispersive X-ray spectrometer EDAX Apollo and a EBSD camera EDAX Hikari. Samples for SEM studies were electropolished in an A2 reagent using Struers Lectropol-5. Further microstructure analysis including selected area electron diffraction (SAED) patterns was performed using the Tecnai G2 F20 transmission electron microscope (TEM). The micro-chemical analysis was conducted using the TEM in scanning transmission electron microscopy (STEM) mode coupled with Integrated Energy-Dispersive X-ray spectroscopy (EDS). Differential thermal analysis (DTA) was carried out with a Setaram SETSYS-18 DTA. A cylindrical sample of 3 mm in diameter and height was placed in an alumina crucible and measured under Ar atmosphere. The sample was heated and cooled seven times using the following heating/cooling rates: 10, 10, 20, 5, 10 °C/min up to 1200 or 1250 °C and back down to room temperature, then 20 °C/min to 1250 °C and continuing with 5 °C/min to 1580 °C, the same back to room temperature and finally 10 °C/min to 1580 °C and back. Calibration measurements were performed using certified standards of pure Al, Au, and Ni resulting in an accuracy of ±1 °C for the measured temperatures. Hardness measurements (with the Vickers method) were carried out using a Zwick/ZHU 250 (HV5) in accordance with (HV) ASTM E 92. Compressive strength tests were performed using an INSTRON 6025 machine according to the PN-57/H-04320 standard on cylindrical samples of 4 mm in diameter and 6 mm in height.
References
Yeh, J. W. et al. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 6, 299–303, doi:10.1002/adem.200300567 (2004).
Cantor, B., Chang, I. T. H., Knight, P. & Vincent, A. J. B. Microstructural development in equiatomic multicomponent alloys. Mat. Sci. Eng. A-Struct. 375-377, 213–218, doi:10.1016/j.msea.2003.10.257 (2004).
Murty, B. S., Yeh, J. W. & Ranganathan, S. High-Entropy Alloys (Butterworth-Heinemann, Boston, 2014).
Zhang, Y. et al. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 61, 1–93, doi:10.1016/j.pmatsci.2013.10.001 (2014).
Gao, M. C., Yeh, J.-W., Liaw, P. K. & Zhang, Y. High-Entropy Alloys: Fundamentals and Applications (Springer, Cham, Switzerland, 2016).
Gludovatz, B. et al. A fracture-resistant high-entropy alloy for cryogenic applications. Science 345, 1153–1158, doi:10.1126/science.1254581 (2014).
Tsai, M.-H. & Yeh, J.-W. High-Entropy Alloys: A Critical Review. Materials Research Letters 2, 107–123, doi:10.1080/21663831.2014.912690 (2014).
Youssef, K. M., Zaddach, A. J., Niu, C., Irving, D. L. & Koch, C. C. A Novel Low-Density, High-Hardness, High-entropy Alloy with Close-packed Single-phase Nanocrystalline Structures. Materials Research Letters 3, 95–99, doi:10.1080/21663831.2014.985855 (2014).
Zou, Y., Ma, H. & Spolenak, R. Ultrastrong ductile and stable high-entropy alloys at small scales. Nat Commun 6, 7748, doi:10.1038/ncomms8748 (2015).
Li, Z., Pradeep, K. G., Deng, Y., Raabe, D. & Tasan, C. C. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 534, 227 (2016).
Gludovatz, B. et al. Exceptional damage-tolerance of a medium-entropy alloy CrCoNi at cryogenic temperatures. Nat Commun 7, 10602, doi:10.1038/ncomms10602 (2016).
Zhang, Z. et al. Nanoscale origins of the damage tolerance of the high-entropy alloy CrMnFeCoNi. Nat Commun 6, 10143, doi:10.1038/ncomms10143 (2015).
Zhang, Y., Zuo, T., Cheng, Y. & Liaw, P. K. High-entropy alloys with high saturation magnetization, electrical resistivity, and malleability. Sci Rep 3, 1455, doi:10.1038/srep01455 (2013).
Lužnik, J. et al. Complex magnetism of Ho-Dy-Y-Gd-Tb hexagonal high-entropy alloy. Phys. Rev. B 92 (2015).
Körmann, F. et al. “Treasure maps” for magnetic high-entropy-alloys from theory and experiment. Appl. Phys. Lett. 107, 142404, doi:10.1063/1.4932571 (2015).
Belyea, D. D., Lucas, M. S., Michel, E., Horwath, J. & Miller, C. W. Tunable magnetocaloric effect in transition metal alloys. Sci Rep 5, 15755, doi:10.1038/srep15755 (2015).
Kozelj, P. et al. Discovery of a superconducting high-entropy alloy. Phys. Rev. Lett. 113, 107001, doi:10.1103/PhysRevLett.113.107001 (2014).
Zhang, Y. et al. Influence of chemical disorder on energy dissipation and defect evolution in concentrated solid solution alloys. Nat Commun 6, 8736, doi:10.1038/ncomms9736 (2015).
Huang, Y.-S., Chen, L., Lui, H.-W., Cai, M.-H. & Yeh, J.-W. Microstructure, hardness, resistivity and thermal stability of sputtered oxide films of AlCoCrCu0.5NiFe high-entropy alloy. Mat. Sci. Eng. A-Struct 457, 77–83, doi:10.1016/j.msea.2006.12.001 (2007).
Senkov, O. N., Scott, J. M., Senkova, S. V., Miracle, D. B. & Woodward, C. F. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J. Alloys Compd. 509, 6043–6048, doi:10.1016/j.jallcom.2011.02.171 (2011).
Chou, Y. L., Yeh, J. W. & Shih, H. C. The effect of molybdenum on the corrosion behaviour of the high-entropy alloys Co1.5CrFeNi1.5Ti0.5Mox in aqueous environments. Corros. Sci. 52, 2571–2581, doi:10.1016/j.corsci.2010.04.004 (2010).
Manzoni, A. et al. Investigation of phases in Al23Co15Cr23Cu8Fe15Ni16 and Al8Co17Cr17Cu8Fe17Ni33 high entropy alloys and comparison with equilibrium phases predicted by Thermo-Calc. J. Alloys Compd. 552, 430–436, doi:10.1016/j.jallcom.2012.11.074 (2013).
Feuerbacher, M., Heidelmann, M. & Thomas, C. Hexagonal High-entropy Alloys. Materials Research Letters 3, 1–6, doi:10.1080/21663831.2014.951493 (2014).
Takeuchi, A., Amiya, K., Wada, T., Yubuta, K. & Zhang, W. High-Entropy Alloys with a Hexagonal Close-Packed Structure Designed by Equi-Atomic Alloy Strategy & Binary Phase Diagrams. Jom 66, 1984–1992, doi:10.1007/s11837-014-1085-x (2014).
Zhao, Y. J. et al. A hexagonal close-packed high-entropy alloy: The effect of entropy. Materials & Design 96, 10 (2016).
Middleburgh, S. C., King, D. M. & Lumpkin, G. R. Atomic scale modelling of hexagonal structured metallic fission product alloys (vol. 2, 140292, 2015). Royal Society Open Science 2 (2015).
Troparevsky, M. C., Morris, J. R., Kent, P. R. C., Lupini, A. R. & Stocks, G. M. Criteria for Predicting the Formation of Single-Phase High-Entropy Alloys. Phys. Rev. X 5 (2015).
Gao, M. C. & Alman, D. E. Searching for Next Single-Phase High-Entropy Alloy Compositions. Entropy 15, 4504–4519, doi:10.3390/e15104504 (2013).
Vidoz, A. E. & Brown, L. M. On work-hardening in ordered alloys. Philos. Mag. 7, 1167–1175, doi:10.1080/14786436208209116 (1962).
Gray, T. G. & Pollock, T. M. “Strain Hardening”. In Intermetallic Compounds - Principles and Practice edited by Westbrook, J. H. & Fleischer, R. L. Vol. 3, pp. 361 (John Wiley & Sons, Ltd, 2002).
Leyens, C. & Peters, M. Titanium and Titanium Alloys (Wiley-VCH, Weinheim, 2003).
Hemphill, M. A. et al. Fatigue behavior of Al0.5CoCrCuFeNi high entropy alloys. Acta Mater. 60, 5723–5734, doi:10.1016/j.actamat.2012.06.046 (2012).
Santodonato, L. J. et al. Deviation from high-entropy configurations in the atomic distributions of a multi-principal-element alloy. Nat Commun 6, 5964, doi:10.1038/ncomms6964 (2015).
Singh, S., Wanderka, N., Murty, B. S., Glatzel, U. & Banhart, J. Decomposition in multi-component AlCoCrCuFeNi high-entropy alloy. Acta Mater. 59, 182–190, doi:10.1016/j.actamat.2010.09.023 (2011).
Feuerbacher, M. Dislocations and deformation microstructure in a B2-ordered Al28Co20Cr11Fe15Ni26 high-entropy alloy. Sci Rep 6, 29700, doi:10.1038/srep29700 (2016).
King, D. M., Middleburgh, S. C., Edwards, L., Lumpkin, G. R. & Cortie, M. Predicting the Crystal Structure and Phase Transitions in High-Entropy Alloys. Jom 67, 2375–2380, doi:10.1007/s11837-015-1495-4 (2015).
Huang, Y. et al. Comparison of mechanical properties of Ni3Al thin films in disordered FCC and ordered L1(2) phases. Acta Mater. 49, 2853–2861, doi:10.1016/S1359-6454(01)00094-5 (2001).
Niu, C. et al. Spin-driven ordering of Cr in the equiatomic high entropy alloy NiFeCrCo. Appl. Phys. Lett. 106, 161906, doi:10.1063/1.4918996 (2015).
Middleburgh, S. C., King, D. M., Lumpkin, G. R., Cortie, M. & Edwards, L. Segregation and migration of species in the CrCoFeNi high entropy alloy. J. Alloys Compd. 599, 179–182, doi:10.1016/j.jallcom.2014.01.135 (2014).
Maiti, S. & Steurer, W. Structural-disorder and its effect on mechanical properties in single-phase TaNbHfZr high-entropy alloy. Acta Mater. 106, 87–97, doi:10.1016/j.actamat.2016.01.018 (2016).
Zhang, F. et al. An understanding of high entropy alloys from phase diagram calculations. Calphad 45, 1 (2014).
Senkov, O. N., Miller, J. D., Miracle, D. B. & Woodward, C. Accelerated exploration of multi-principal element alloys for structural applications. Calphad 50, 32–48, doi:10.1016/j.calphad.2015.04.009 (2015).
Laurent-Brocq, M., Perriere, L., Pires, R. & Champion, Y. From high entropy alloys to diluted multi-component alloys: Range of existence of a solid-solution. Materials & Design 103, 84 (2016).
Kaufman, L. & Bernstein, H. Computer Calculation of Phase Diagrams (Academic, New York, 1970).
Saunders, N. & Miodownik, A. P. Calphad (Calculation of Phase Diagrams): A Comprehensive Guide (Pergamon, Oxford, 1998).
Rogal, Ł., Czerwinski, F., Jochym, P. T. & Litynska-Dobrzynska, L. Microstructure and mechanical properties of the novel Hf25Sc25Ti25Zr25 equiatomic alloy with hexagonal solid solutions. Materials & Design 92, 8 (2016).
Oh, H. et al. Lattice Distortions in the FeCoNiCrMn High Entropy Alloy Studied by Theory and Experiment. Entropy 18, 321, doi:10.3390/e18090321 (2016).
Körmann, F. & Sluiter, M. Interplay between Lattice Distortions, Vibrations and Phase Stability in NbMoTaW High Entropy Alloys. Entropy 18, 403, doi:10.3390/e18080403 (2016).
Körmann, F., Ruban, A. V. & Sluiter, M. H. F. Long-ranged interactions in bcc NbMoTaW high-entropy alloys. Materials Research Letters 5, 35–40, doi:10.1080/21663831.2016.1198837 (2017).
Song, S. G. & Gray, G. T. Structural interpretation of the nucleation and growth of deformation twins in Zr and Ti—II. Tem study of twin morphology and defect reactions during twinning. Acta Metall. Mater. 43, 2339–2350, doi:10.1016/0956-7151(94)00434-X (1995).
Nave, M. D. & Barnett, M. R. Texture change near grain boundaries and triple points in cold-rolled interstitial-free steel. Mat. Sci. Eng. A-Struct. 386, 244–253, doi:10.1016/S0921-5093(04)00962-1 (2004).
Partridge, P. G. The crystallography and deformation modes of hexagonal close-packed metals. Metallurgical Reviews 12, 169 (2013).
Dimcic, B., Vilotijevic, M., Bozic, D., Rajnovic, D. & Jovanovic, M. T. Microstructural and mechanical properties of Ti3Al-based intermetallics produced by powder metallurgy. Current Research in Advanced Materials and Processes 494, 211 (2005).
H., W. J. & Fleischer, R. L. (eds), Basic Mechanical Properties and Lattice Defects of Intermetallic Compounds (Wiley, 1995).
Sastry, S. M. L. & Lipsitt, H. A. Ordering transformations and mechanical properties of Ti3Ai and Ti3Al-Nb alloys. Metall. Trans. A 8, 1543 (1977).
Leuthold, J. Mechanisms of time dependent plasticity in ultra-fine grained copper after severe plastic deformation, PhD thesis, Münster University (2016).
Lipsitt, H. A., Shechtman, D. & Schafrik, R. E. The Deformation and Fracture of Ti3AI at Elevated Temperatures, Metall. Trans. A 11, 1369 (1980).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comp. Mater. Sci. 6, 15 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186, doi:10.1103/PhysRevB.54.11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979, doi:10.1103/PhysRevB.50.17953 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868, doi:10.1103/PhysRevLett.77.3865 (1996).
Zunger, A., Wei, S., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. Phys. Rev. Lett. 65, 353–356, doi:10.1103/PhysRevLett.65.353 (1990).
Methfessel, M. & Paxton, A. T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B 40, 3616–3621, doi:10.1103/PhysRevB.40.3616 (1989).
Vinet, P., Ferrante, J., Rose, J. H. & Smith, J. R. J. Geophys. Res. [Solid Earth Planets] 92, 9319 (1987).
Mermin, N. D. Thermal Properties of the Inhomogeneous Electron Gas. Phys. Rev. 137, A1441–A1443, doi:10.1103/PhysRev.137.A1441 (1965).
Wolverton, C. & Zunger, A. First-principles theory of short-range order, electronic excitations, and spin polarization in Ni-V and Pd-V alloys. Phys. Rev. B 52, 8813–8828, doi:10.1103/PhysRevB.52.8813 (1995).
Zhang, X., Grabowski, B., Körmann, F., Freysoldt, C. & Neugebauer, J. “Accurate electronic free energies of the 3d, 4d, and 5d transition metals at high temperatures”. Phys. Rev. B 95, 165126, doi:10.1103/PhysRevB.95.165126 (2017).
Ma, D., Grabowski, B., Körmann, F., Neugebauer, J. & Raabe, D. Ab initio thermodynamics of the CoCrFeMnNi high entropy alloy: Importance of entropy contributions beyond the configurational one. Acta Mater. 100, 90–97, doi:10.1016/j.actamat.2015.08.050 (2015).
Schuster, J. C. & Palm, M. Reassessment of the binary Aluminum-Titanium phase diagram. J. Phase Equilib. Diffus. 27, 255–277, doi:10.1361/154770306X109809 (2006).
Predel, B. “Hf-Sc (Hafnium-Scandium)”, In Landolt-Börnstein - Group IV Physical Chemistry, edited by Madelung, O. (Springer Berlin Heidelberg, Berlin, Heidelberg, 1996).
Haynes, W. M. (ed), CRC Handbook of Chemistry and Physics (CRC Press, Taylor & Francis Group, Boca Raton, 2015).
Acknowledgements
We thank Andrei V. Ruban for providing the spcm program for generating the special quasi-random structures. We thank Matthias Wegner and Daniel Gaertner for performing the tensile tests and fracture surface characterization, and Gerhard Wilde for fruitful discussions. The research was supported by the Polish science financial resources, The National Science Centre, Poland, project title: “Development of new high entropy alloys with dominant content of hexagonal solid solutions” project number: 2014/15/D/ST8/02638. Funding by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 639211) and by the scholarship KO 5080/1–1 of the Deutsche Forschungsgemeinschaft (DFG) are gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
F.K. and B.G. performed the thermodynamic analysis and the ab initio simulations. L.R. prepared the alloys and performed the TEM and X-ray investigations. L.R. and S.D. performed the mechanical studies. P.B. performed the SEM and EBSD measurements. F.S. performed the calorimetric measurements. L.R., F.K., S.D., and B.G. prepared the manuscript. All authors approved the final manuscript for submission.
Corresponding authors
Ethics declarations
Competing Interests
The authors declare that they have no competing interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rogal, L., Bobrowski, P., Körmann, F. et al. Computationally-driven engineering of sublattice ordering in a hexagonal AlHfScTiZr high entropy alloy. Sci Rep 7, 2209 (2017). https://doi.org/10.1038/s41598-017-02385-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-017-02385-w
This article is cited by
-
Performance of two complementary machine-learned potentials in modelling chemically complex systems
npj Computational Materials (2023)
-
Centrosymmetric to noncentrosymmetric structural transformation in a superconducting high-entropy alloy due to carbon addition
Science China Materials (2023)
-
Entropy versus enthalpy in hexagonal-close-packed high-entropy alloys
Rare Metals (2022)
-
Settling the matter of the role of vibrations in the stability of high-entropy carbides
Nature Communications (2021)
-
Stacking fault energy of basal plane for hexagonal closed-packed medium entropy alloy ZrHfTi: Ab initio prediction
Applied Physics A (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.