Introduction

The behavior of atoms, molecules, nano-systems, and solids in intense laser fields1–14 continues to reveal new dynamics. Atoms and molecules whose valence electrons can absorb several photons fall in the multiphoton ionization regime class when the Keldysh parameter γ ≫ 1 (γ = (Ip/2Up)1/2, where Up is the laser field’s ponderomotive potential and Ip is the ionization potential). Those systems whose valence electrons tunnel through the potential barrier formed by the laser field and the Coulomb force, fall within the class of tunneling or over the barrier ionization, depending upon the laser field intensity5, and with Keldysh parameter γ ≪ 16–10.

Endohedral, or doped fullerenes, which is the topic of this Scientific Report, are intriguing systems that bridge the gap between molecular and nano-systems15–18. However, little is known about their structure and dynamics when excited with a strong laser field. Among their properties, electron transfer from the encaged species to the carbon cage is of special interest15, 16. The understanding derived from the photoionization of these carbon nanomaterials enables optimizing their properties, which is relevant to their use in molecular electronics and organic photovoltaics19. These nanoscale systems have received attention because they can be used for applications ranging from medical usage20 such as in imaging or drug delivery, to their employment in devices for quantum computing21. Our interest in investigating these systems stems from the possibility of finding novel fundamental effects making their examination a focus of fundamental research15, 16, 19, 22. In fact, we show with this experimental work that doped fullerenes respond differently to intense I.R. laser fields compared to empty fullerenes. Furthermore, with our quantitative calculations, we explain in detail why their behavior is different. This work falls within the general, active topic of non-linear physics23–33.

In recent years, non-linear physics or strong-field laser research has led to technological advances and novel phenomena23–33. Investigations of the behavior of molecules in short, intense laser fields5, 10, 34 were extended to complex molecules, such as C60, which has been challenging35–44 due to the many electron-nuclei response it exhibits since it is a cage of 60 atoms with 240 valence electrons. The photoionization mechanisms have been found to be wavelength and pulse duration dependent37, 38, 45. For IR pulses (800 nm) of about 30 fs duration and intensities below 5 × 1013 W/cm2, it was found that multiphoton processes dominate when ionizing C60, while tunneling, and/or over-the barrier-ionization, or ionization due to induced electron re-collision36 are not probable under these conditions. The single-active-electron (SAE) method was used to calculate the ionization of C60 in intense, 4 × 1013 W/cm2, laser pulses with durations between 27 and 70 fs and for a wide range of wavelengths ranging from 395–1800 nm39 which agreed with measurements by Shchatsinin et al. 40. For a long I.R. wavelength of 1800 nm and 70 fs pulse duration, the SAE picture predicts “over the barrier” ionization for a peak intensity of 1015 W/cm2 leading to non-fragmented but highly charged C60 q+ (q = 1–12)35. At short wavelength of 355 nm, the excitation of C60 with 10 ns pulses leads to fragmentation by delayed ionization and C2 emission as well as other fragments even for small intensities of about 2 × 106 W/cm2  43. The use of electron spectroscopy in addition to the ion measurements raised questions for the C60 investigations; namely, can the ionization and fragmentation dynamics be adequately modeled in the SAE picture or should multi-electron dynamics be included40, 44? This led to recent experimental and theoretical investigation, which concluded that both SAE and many-electron effects, are important36.

Our motivation for this work is to contribute substantially to the field of non-linear physics by investigating increased complexity targets. We studied the photoionization of endohedral fullerenes in strong laser fields to answer the following question: Do the ionization dynamics change in fs strong laser fields for a doped fullerene compared to C60, an empty fullerene and why? We use a prototype, Ho3N@C80, interacting with intense (0.1–5 × 1014 W/cm2), short (30 fs), 800 nm laser pulses giving rise to multiply charged parent ions as well as fragment ions. We focus here on the measurement and theoretical explanation of the power law for singly ionized Ho3N@C80 yields, and compare our findings to C60 results (because pristine C80 is not commercially available) carried out under similar conditions40. Two distinct regions are present in the ion yield spectra with respect to field strength corresponding to different ionization mechanisms and power laws. For low field strengths, multiphoton ionization dominates, while for higher field strengths, tunneling and ionization over the barrier are the main ionization processes. The photoelectron spectra of endohedral fullerenes such as Li@C60 18 or Sc3N@C80 46 have been measured with longer and weaker laser pulses. Although the photoionization of endohedral fullerenes was studied by other groups13, 14, 18, 46, none of the cases studied the role of encaged atoms or clusters in femtosecond strong laser fields. As one would expect, encaging of an atom or cluster in a carbon cage modifies the electronic structure of the fullerene, but in what way? Previously, for C60, both SAMO and Rydberg states played important roles when exposed to a strong laser field45. Both kinds of states can be indirectly populated by vibronic coupling, but because the density of Rydberg states is higher than that of SAMO states, Rydberg state ionization in C60 dominates the ionization at laser intensities >1013 W/cm2  45, which brought up an interesting question: do the SAMO states play a more important role in a doped fullerenes such as Ho3N@C80? In this work, supported by theory, we demonstrate and explain that the endohedral fullerene Ho3N@C80 responds differently to intense near-infrared femtosecond laser fields compared to C60, because of the increased importance of the SAMO states and this is reflected by a different slope of the power law for low field strengths.

A power law corresponding to n = 5 photon was measured in C60 while we report here a power law of n = 3 photons for Ho3N@C80. In C60 the power law is readily understood from energetics: it takes 5 photons of 1.55 eV (800 nm) to reach the IP, 7.6 eV40. However, in Ho3N@C80 (experimental IP ~ 6.9 eV)44, 45, instead of observing a power law corresponding to 5 photons, we demonstrate below a power law corresponding to n = 3. This decrease arises from resonance-enhanced multiphoton ionization of intermediate states that promptly ionize by absorption of an extra photon. We argue these states are Super Atomic Molecular Orbital (SAMO) states similar to the ones observed in C60 13, 47. The SAMO states are excited electronic states where a valence electron is promoted to a diffuse atomic-like molecular orbital. They are present in both fullerenes and characterized by very short photoionization lifetimes, in the few fs range, because of their diffuse character11, 13, 48. However, unlike in Ho3N@C80, the lower SAMO states of s, p, and d symmetry are dark states in C60 because of their spherical symmetry and cannot be accessed during the pulse. They can only be populated by vibronic coupling on a time scale of few tens of fs. On the contrary, SAMO states of Ho3N@C80 become optically active because of symmetry breaking induced by the inclusion of Ho3N inside the symmetric but non-spherical C80 fullerene cage. We show below that the optically active SAMO states in Ho3N@C80 can be accessed by the absorption of 3 photons during the pulse. Upon absorption of these 3 photons, the SAMO states of Ho3N@C80 almost instantaneously photoionize, which makes photoexcitation the rate limiting step and explains the n = 3 observed power law. Note that the only theoretically calculated IPs available in the literature are 6.88 eV for Sc3N@C80 49 and 6.93 eV for Lu3N@C80 50. All of these values are very close to 6.84 eV for the C80 molecule51.

The experiment was performed using an ion velocity map imaging (VMI) spectrometer used in the time of flight (TOF) mode and details are available in the Supplementary information (S.I.) and in refs 52 and 53. The ion-mass spectrum of Ho3N@C80 at 800 nm obtained at a laser intensity of 4 × 1014 W/cm2 and 30 fs pulse duration is shown in Fig. 1. We observe parent ions up to Ho3N@C80 4+ although the statistics is low for Ho3N@C80 4+. We also observed Ho-based molecular fragment ions: HoC2 +, HoCN+, and HoC4 +, as well as atomic Ho+ ions (the most abundant) created by bond breaking and bond forming. In this report, we focus on the parent ion yield power laws.

Figure 1
figure 1

Mass/charge spectra of Ho3N@C80 ionized with laser pulses of 800 nm, 30 fs pulse duration and an intensity of 4 × 1014 W/cm2.

Full size image

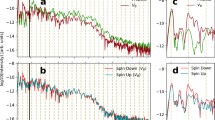
In this work, we investigated the dependence of Ho3N@C80 q+ (q = 1–2) yields as a function of the peak laser intensity and our results are shown in Fig. 2. We find that the yields for Ho3N@C80 ions follow the power law Y = In as a function of laser field intensity I40, 42. To determine the power laws, linear fits were applied to the experimental ion yields using a least-squares fit for intensities higher than 1.2 × 1014 W/cm2. Then, the rest of the data, which significantly deviated from the power law at high intensity, were fit by lines with different slopes. The fitting errors for the Ho3N@C80 ions are shown in Fig. 2. The observed slopes for q = 1, 2 at lower intensities (<1.2 × 1014 W/cm2) are 3.0 ± 0.1 and 5.7 ± 0.5, respectively and are summarized in Table 1. The intensity at the cross point of the two slopes is defined as the saturation intensity42. As the intensity increases beyond saturation for each of the ion species, the yields start to follow an almost linear trend with a shallower slope, indicating that the ionization saturation has been reached39, 54.

Figure 2
figure 2

Comparison of the ion yield dependence on peak intensity for the ionization of Ho3N@C80 q+ (q = 1, 2) (filled symbols) and C60 q+ (q = 1, 2) (open symbols). The Ho3N@C80 q+ results are extracted from data in Fig. 1 and the yields of Ho3N@C80 with a charge q = 1 is multiplied by 5. The C60 data are from ref. 40 and the C60 + yield was multiplied by 2 for clarity.

Full size image
Table 1 Measured power laws for HoN3@C80 and for C60 40 ion charge states.
Full size table

To check our findings, we performed a simulation of the ion yield of singly charged Ho3N@C80 through three-photon resonant ionization, taking focal volume averaging into account. The generalized 3-photon cross section σ3 is defined by the ionization probability per unit detection volume, W(t) = σ3(I/hν)3. Experimental parameters used in the simulation are laser focal waist (20 µm), pulse duration (30 fs), and diameter of the molecular beam (4 mm). The yield of singly charged Ho3N@C80 was obtained by integrating the ionization rate in the interaction region. By adjusting the cross section σ3, we obtained a reasonable result shown as the red dashed line in Fig. 2. We note that within the accuracy of the parameters, the result of the simulation does not significantly change.

The strong field ionization (SFI) mechanisms of Ho3N@C80 with the current IR laser conditions include multiphoton, tunneling, and over the barrier ionization, based on our computation of the barrier lowering induced by the strong field. We find that the multiphoton ionization mechanism dominates at low laser intensities (<5 × 1013 W/cm2, corresponding to γ > 1.0) and tunnel ionization5 dominates at high laser intensities (>1014 W/cm2, corresponding to γ < 0.75). In the intermediate region, where γ varies between 1.0 and 0.75, there is a complex interplay among the multiphoton, tunneling, over the barrier mechanisms as well as ionization saturation.

In Fig. 2, we compare power law slopes for the doped fullerene results with that of C60. The wavelength of the laser used in both experiments was 800 nm, while the laser pulse duration in the C60 experiment was 27 fs, close to the 30 fs used in the current experiment and within the error bar. The error bar on the laser intensity was 15%. As can be seen from Table 1, the slopes of power law are substantially higher for the ionization of C60 compared to Ho3N@C80.

Electronic structure computations were performed to elucidate the power law difference between C60 and Ho3N@C80. The equilibrium geometry of the Ho3N@C80’s isomers was computed at the DFT/PBE055 level (see computational details in S.I.). The starting geometries were obtained by adding the Ho3N complex inside each of the six C80 isomers. The most stable isomer has a slightly triangular C80 cage with the nitrogen atom localized at the center, and a Ho-N bond length of 2.06 Å (the shortest compared to the other stable isomers). The inclusion of the Ho3N complex in the cage induces a significant lowering of the symmetry. The bare C80 belongs to the D5h point group while Ho3N@C80 exhibits an approximate C2 symmetry (see S.I. for details). The computed vertical ionization potential (IP) of the lowest energy isomer is 6.54 eV, which is close to the experimental IP of the C80 fullerene (6.84 eV)51. The ionization potentials of the other isomers are significantly lower, see Table S1 in the S.I. In the following discussion, we only refer to the lowest energy isomer. Similar doped fullerenes such as Y3N@C80 56 and Lu2CeN@C80 50 exhibit a triangular cage and a similar ionization potential.

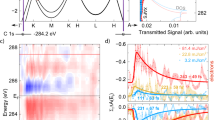
The electronic structures of the 250 lowest SAMO and valence excited electronic states of Ho3N@C80’s most stable isomer were computed in TDDFT with the LC-BLYP functional57, 58 (see computational details in the S.I., note that no Rydberg states are present in the band because their computation requires a larger basis of atomic orbitals that includes more highly diffuse basis functions). Particular attention was given to the excited states coined as super-atom-molecular orbital (SAMO) states47. SAMO excited states were first discovered for the case of fullerenes on metal surfaces47. They are diffuse hydrogen-like orbitals resulting from the shallow potential present at the center of hollow systems such as fullerenes11, 13, 14, 47. The SAMO excited states are different from other Rydberg states because of the significant electronic density localized inside the carbon cage as shown in Fig. 3(a,b). They were called SAMOs because for C60, they exhibit the spherical harmonic shapes s, p, or d atomic orbital symmetry47. For C60 adsorbed on surfaces47 and in the gas phase13, 14, sharp bands of s, p, and d SAMO’s were identified48. Due to the symmetry breaking induced by the insertion of the Ho3N inside the cage, in the case of Ho3N@C80, there is a broad manifold of excited states with delocalized diffuse orbitals of type s, p, and d, analogous to the C60’s SAMO states. For this reason, we also named these states SAMO but they are not pure s, p, or d SAMO states as in C60 because the presence of Ho3N induces a mixing of the SAMO states with the valence states as shown in Fig. 3a. Moreover, unlike those of C60, the SAMO states in Ho3N@C80 are optically active because of the symmetry breaking of the cage. For instance, the transition dipole moment between the ground state and the s SAMO state is close to zero in C60 and C80 while it is 0.66au in Ho3N@C80 (Table 2).

Figure 3
figure 3

(a) Dyson orbitals of a typical valence state, s SAMO, p SAMO and d SAMO states of Ho3N@C80 with an isocontour of 0.002|e|/Å. (b) Charge density of the Dyson orbitals of panel a. (c) Density of SAMO states as a function of the excitation energy. The electronic states and Dyson orbitals have been computed in TDDFT at the LC-BLYP/6–31G(d) + ECP56MWB/7s6p5d for Ho + Bq (6–31(6+)G(d)) level for Ho3N@C80’s lowest energy isomer shown in the inset.

Full size image
Table 2 Computed binding energies, photoionization lifetimes (in fs) for a field intensity of 1013 and 1014 W/cm2 and transition dipole moments (μtrans) between the ground and excited states shown in Fig. 3.
Full size table

As can be seen in Fig. 3(c), the number of SAMO states increases with the excitation energy and reaches a maximum at about 5.75 eV. The lowest SAMO state of Ho3N@C80 has an excitation energy of 4.98 eV and a non-zero transition dipole moment, like all the SAMO states, so that it can be directly accessed from the ground state during the pulse. Its excitation energy corresponds to 3.2 photons but the laser pulse has a FMHW width of 0.15 eV (per photon) so that this state can directly be accessed through 3-photon absorption during the pulse.

Once the SAMO states are photoexcited during the pulse, they can promptly ionize due to their short photoionization lifetime (i.e. the time it takes to photoionize 63% of the population). The lifetimes, that are inversely proportional to the square modulus of the photoionization coupling elements V, have been computed for the 250 lowest excited states of Ho3N@C80 using the formalism described in references59, 60.

$${\bf{V}}(\varepsilon )={E}_{0}\langle {\varphi }^{Dyson}|{\bf{E}}\cdot {\bf{r}}|{\chi }^{electron}(\varepsilon )\rangle $$
(1)

Here, E0 is the electric field amplitude, E the electric field polarization vector, χelectron (ε) the wavefunction of the ionized electron and ϕ Dyson is the Dyson orbital11, 48, 61, 62, which is the overlap between the neutral and cationic wavefunctions. The Dyson orbitals provide a correlated view of the wave function of the ionized electron and play a crucial role in the interpretation of photoelectron lifetimes and angular distributions. We find that the Dyson orbitals of the SAMO states (Fig. 3a) in Ho3N@C80 have a small valence character and are distorted compared to the ones of the spherical C60 fullerene due in part to the loss of symmetry of the slightly triangular C80 cage but primarily to the inclusion of Ho3N inside the C80 cage (Fig. 4a). The presence of Ho3N drastically changes the amount of charge density of the Dyson orbital inside the cage compared to that of the bare C60. For instance, in C60 the charge density of the s SAMO is maximal at the center of cage (r = 0) while in Ho3N@C80, the nitrogen lies at the center of the cage so the s SAMO charge density is zero at r = 0 and then increases.

Figure 4
figure 4

Photoionization lifetime (field intensity of 1013 W/cm2) for a set of representative SAMO and valence states, plotted as a function of the kinetic energy of electron ionized from the SAMO or valence states. Amongst the valence states, some are isoenergetic with the SAMO states (see S.I. for details).

Full size image

In Eq. 1, the Coulomb interaction between the fullerene cage and the departing electron is neglected, which can affect the momentum of the leaving electron, especially for low kinetic energy electrons. Within this approximation, the wavefunction of the electron is described by an orthogonalized plane wave. Previous work on C60 showed that the relative photoionization intensities of SAMO states computed using this approximation were in good agreement with the experimental values63, which suggests a minor role of the Coulomb interactions for kinetic energy of the photoelectrons ranging from 0.2 to 1.55 eV. From Eq. 1, we can readily compute the lifetimes that are inversely proportional to the field intensity and to the dipole coupling between the Dyson orbital and the ionized electron. Due to their simple hydrogenoid shape, the SAMO states have a large dipole coupling compared to the isoenergetic valence excited states48, which leads to lifetimes several orders of magnitude smaller than the ones of the isoenergetic valence excited states (see Table 2 and Fig. 4(c)). For a field intensity of 1013 W/cm2, the SAMO states have lifetimes on the order of a femtosecond, which is short compared to several hundreds of fs for the valence states. When the SAMO states are populated, they promptly ionize, unlike the valence states that slowly ionize during the pulse. The limiting rate determining step for the SAMO states is their photoexcitation while for the valence states it is their photoionization. The SAMO state lifetimes strongly depend on the kinetic energy of the ionized electron and increase faster than the valence state lifetimes. Nevertheless, even for a kinetic energy of 1.55 eV (≈one IR photon), the SAMO states still ionize on average 35 times faster than the valence states.

For low laser intensities, the slope of the power law in the photoionization region is expected to be the number of photon necessary to ionize the ground state, as it is the case in C60 and which should be 5 for Ho3N@C80. However, the observed value of “n” is found to be 3 (Table 1), which indicates there are intermediates resonant states64 in the photoionization process. These states could be valence or SAMO excited states because they both are optically active (Table 2) and can therefore be transiently populated during the pulse. However, the SAMO states have lifetimes around two orders of magnitude shorter than the valence states so if both type of states are populated during the pulse, ionization would mainly come from the SAMO states. Thus the SAMO states act as fast ionizing intermediate resonant states, which affects the power law, as the rate-determining step is now the photoexcitation process to the SAMO states instead of the photoionization as is the case of C60. Such a process does not occur in C60 because the SAMO states are not optically active so they cannot be promptly excited from the ground state by direct multiphoton excitation. They can only be populated indirectly by vibronic coupling to isoenergetic optically active valence states14, which takes several tens of fs. Therefore, the transient population in the SAMO states during the pulse is larger in Ho3N@C80 than in C60, and so is the ion yield as shown in Fig. 2.

It is known that strong laser fields can induce vibrations in C60 ions65. Vibrational excitation and significant geometric distortion66 may shift the ionization potential of C60. However, the laser intensity used in this report is much smaller than the one used in reference65. It is thus unlikely that the ionization of the parent molecules was affected by the ionization potential change due to the small vibrational energy accumulated during the laser pulse65.

For laser intensities higher than 1014 W/cm2, where γ < 0.75, ionization over the barrier and tunnel ionization are the main mechanisms. Therefore, the ion yields of Ho3N@C80 and C60 are of the same order because it does not depend anymore on the photoexcitation of the SAMO states during the pulse. In the intermediate region, for field intensity ranging from 5 × 1013 − 1 × 1014 W/cm2, both multiphoton and over the barrier ionization mechanisms coexist. The change of mechanisms is reflected in the ion yield that reaches saturation around 9 × 1013 W/cm2 for Ho3N@C80. At this field intensity, we computed a lowering of the IP (second order stark shift) of 1.9 eV, which means that some of the valence states with a slightly higher binding energy than the lowest SAMO states can ionize over the barrier. These states can be accessed by one photon less than the SAMO states and they have transition dipole moments from the ground state up to 5 times larger, which can explain the saturation observed.

In summary, this experimental and theoretical work examined the interaction of a complex system, an endohedral fullerene with short, intense laser pulses, revealing fundamental differences compared to the case of an empty cage such as C60. We explain quantitatively that the clear signature difference is directly linked to the role of SAMO states in both molecules. Although the dominant photoionization mechanism is multiphoton ionization for both fullerenes, the measurement of the laser intensity power law dependence, In, of the singly and doubly charged Ho3N@C80 molecule was interestingly found to be different compared to C60. This difference was explained in detail for Ho3N@C80 + using TDDFT calculations, revealing that SAMO states act as intermediate resonances with larger photoionization widths compared to isoenergetic valence excited states. Both the C60 and Ho3N@C80 SAMO states have photoionization lifetimes of the order of the fs for field intensity higher than 1013 W/cm2. The optically active Ho3N@C80 states can quickly ionize during the 30 fs pulses because they are populated, unlike C60’s SAMO states that can only be populated indirectly by vibronic coupling. The SAMO states of Ho3N@C80 can be optically accessed during the short pulse duration because of their non-zero transition dipole moments, resulting from the symmetry breaking. This experimental and theoretical work demonstrated that the photoionization of a doped fullerene in strong field has a clear signature difference compared to the case of empty C60 13, 14 and of C60 adsorbed on surfaces47. Furthermore, this work has revealed that an encapsulated molecule inside a cage breaks the fullerene symmetry leading to different photo-dynamics and this result should be general for these nano-systems excited under similar conditions. In addition to contributing new knowledge to the active topic of strong field research, our work on doped fullerenes connects to other areas of science since it impacts the understanding of these nano-systems, which have shown the promise to be used in the design of molecular electronics and optoelectronics materials47, 67, 68 as well as used for applications ranging from medical usage20 such as in imaging or drug delivery, and in devices for quantum computing21.