Abstract
Multimodal neuroimaging grants a powerful window into the structure and function of the human brain at multiple scales. Recent methodological and conceptual advances have enabled investigations of the interplay between large-scale spatial trends (also referred to as gradients) in brain microstructure and connectivity, offering an integrative framework to study multiscale brain organization. Here, we share a multimodal MRI dataset for Microstructure-Informed Connectomics (MICA-MICs) acquired in 50 healthy adults (23 women; 29.54 ± 5.62 years) who underwent high-resolution T1-weighted MRI, myelin-sensitive quantitative T1 relaxometry, diffusion-weighted MRI, and resting-state functional MRI at 3 Tesla. In addition to raw anonymized MRI data, this release includes brain-wide connectomes derived from (i) resting-state functional imaging, (ii) diffusion tractography, (iii) microstructure covariance analysis, and (iv) geodesic cortical distance, gathered across multiple parcellation scales. Alongside, we share large-scale gradients estimated from each modality and parcellation scale. Our dataset will facilitate future research examining the coupling between brain microstructure, connectivity, and function. MICA-MICs is available on the Canadian Open Neuroscience Platform data portal (https://portal.conp.ca) and the Open Science Framework (https://osf.io/j532r/).
Measurement(s) | Brain anatomy • Brain activity • Diffusion • Brain microstructure • Functional connectivity • Structural connectivity |
Technology Type(s) | magnetic resonance imaging (MRI) • Functional Magnetic Resonance Imaging • Diffusion Weighted Imaging • magnetic resonance imaging (MRI) • Resting State Functional Connectivity Magnetic Resonance Imaging • Diffusion Weighted Imaging |
Sample Characteristic - Organism | Homo sapiens |
Similar content being viewed by others
Background & Summary
The human brain is a highly interconnected network which can be described at multiple spatial and temporal scales. Neuroimaging, in particular magnetic resonance imaging (MRI), has provided a window into brain structure and function, offering versatile contrasts to assess its multiscale organization1. Multimodal imaging increasingly capitalizes on sequences sensitive to brain microstructure, such as quantitative T1 (qT1) relaxation mapping. This contrast can differentiate highly myelinated regions, with shorter T1 relaxation times, from more lightly myelinated regions showing longer qT12. Regional variations in qT1 concord with seminal myeloarchitectonic studies3,4,5, supporting the potential of these contrasts for in vivo microstructural profiling and the study of myeloarchitectonic similarity between areas6,7,8,9. These investigations can also be complemented by metrics such as geodesic distance, enabling estimations of cortico-cortical wiring cost emerging from short-range intracortical axon collaterals10,11,12,13, the exploration of the anatomical proximity of different brain systems, and the study of cortical topographic organization14,15. In addition, macroscale connectome architecture can be probed using diffusion MRI tractography and resting-state functional connectivity analysis to approximate whole-brain structural and functional networks16,17,18. Together, these techniques offer key insights into overarching principles of brain organization, from properties of local regions to their embedding within macroscale systems.
Recent methodological and conceptual advances have provided the means to analyse topographic principles of multiscale brain organization. Homogeneity in regional properties can be detected in structural and functional imaging data, at the basis of parcellation-based approaches19. Regional boundaries can be defined with a varying level of granularity from different features, such as morphology20,21, microstructure22,23, connectivity patterns24,25, and combinations of these metrics26. Functional and anatomical relationships between parcels can then be identified, forming the brain’s macroscale network architecture27,28,29. Complementing techniques highlighting discrete collections of areas through parcellation or decomposing the brain into mesoscale communities, recent work has begun to identify continuous spatial trends – also referred to as gradients – in brain microstructure, connectivity, and function. Gradient identification approaches have described main axes of cortical and subregional organization at the level of resting-state functional connectivity14,30,31,32,33,34,35, structural connectivity derived from diffusion tractography10,36,37,38, similarity of cortical microstructure6,7,10,39,40,41 and cortical morphology40, as well as molecular and microcircuit properties16,42,43. These approaches have enabled the discovery of a principal gradient of intrinsic functional connectivity differentiating lower-order sensorimotor systems from transmodal systems such as the default-mode network and paralimbic cortices, recapitulating seminal models of the cortical hierarchy formulated in non-human primates7,44,45. By depicting low dimensional axes of cortical organization, gradient approaches enable investigations of systematic changes in structure and function across the brain and are thus particularly suited for studies aiming to bridge different neurobiological axes. For instance, recent work has demonstrated stronger decoupling between principal microstructural and functional gradients in transmodal cortical areas relative to unimodal systems, possibly reflective of the flexible role that transmodal areas play in human cognition7. Relatedly, the principal functional gradient has also been shown to reflect variations in geodesic distance between sensory and transmodal systems, offering a potential macroscale mechanism allowing transmodal networks to support higher cognitive functions decoupled from “the here and now”14. By offering a formal framework for such multimodal comparisons, these findings emphasize the potential of dimensional analyses to obtain novel insights into multiscale brain organization.
Beyond innovations in imaging and analytics, neuroscience has increasingly benefitted from the adoption of open science practices, particularly through open data sharing46,47,48 and the combined publication of derivative data and their associated pre-processing pipelines49. In recent years, the field has witnessed the emergence of numerous and widely used data sharing initiatives for multimodal MRI data, such as the Human Connectome Project46, UK BioBank47, NSPN48, Cam-CAN50, ABIDE51,52, and many others. In parallel, data sharing efforts have been supported by advances in methods and infrastructure supporting new data releases49,53,54,55 facilitating exchange and collaboration while boosting transparency and reproducibility in neuroimaging56. In line with this perspective, this work presents a ready-to-use multimodal MRI dataset for Microstructure-Informed Connectomics (MICA-MICs). MICA-MICs provides connectomes based on i) task-free functional MRI, ii) diffusion tractography, iii) microstructure covariance analysis based on qT1 mapping, and iv) geodesic cortical distance, each built across multiple parcellation schemes and spatial scales. We furthermore provide anonymized raw data adhering to Brain Imaging Data Structure (BIDS) standards57. Processing has been carried out using an open access pipeline (https://micapipe.readthedocs.io/). This resource promises to deepen our understanding of the human brain at multiple scales and augment assessments of generalizability and replicability.
Methods
Participants
Data were collected in a sample of 50 healthy volunteers (23 women; 29.54 ± 5.62 years; 47 right-handed) between April 2018 and February 2021. Each participant underwent a single testing session. All participants denied a history of neurological and psychiatric illness. The Ethics Committee of the Montreal Neurological Institute and Hospital approved the study (2018–3469). Written informed consent, including a statement for openly sharing all data in anonymized form, was obtained from all participants. Socio-demographic information included in this release includes participant sex and age at time of scan (in 5-year increments).
MRI data acquisition
Scans were completed at the Brain Imaging Centre of the Montreal Neurological Institute and Hospital on a 3 T Siemens Magnetom Prisma-Fit equipped with a 64-channel head coil. Participants underwent a T1-weighted (T1w) structural scan, followed by multi-shell diffusion-weighted imaging (DWI) and resting-state functional MRI (rs-fMRI). In addition, a pair of spin-echo images was acquired for distortion correction of individual rs-fMRI scans. A second T1w scan was then acquired, followed by qT1 mapping (Fig. 1a). Total scan time for these acquisitions was approximately 45 minutes.
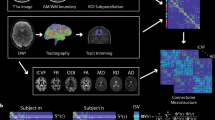
(a) Sequences provided in the MICA-MICs dataset release include quantitative T1 relaxometry, a multiband accelerated resting-state functional scan, multiband, multi-shell diffusion-weighted imaging, and two structural T1w scans. Pial and white matter surface segmentations are superimposed on a coronal slice of the T1w image generated by FreeSurfer combining both input T1w scans. (b) Group-averaged matrices (only left hemisphere parcels shown - top panel) and connection weights from three outlined seeds, selected to represent a diverse set of network communities (bottom panel). Microstructural profile covariance (MPC), functional connectivity (FC), and geodesic distance (GD) matrices were averaged across participants. Group-level structural connectivity (SC) was computed using distance-dependent thresholding to preserve the distribution of within- and between-hemisphere connections lengths in individual subjects90. Prior to averaging, subject-level SC matrices were log-transformed to reduce connectivity strength variance. All features are projected to the fsaverage5 midsurface from the Schaefer-400 atlas.
Two T1w scans with identical parameters were acquired with a 3D magnetization-prepared rapid gradient-echo sequence (MP-RAGE; 0.8 mm isotropic voxels, matrix = 320 × 320, 224 sagittal slices, TR = 2300 ms, TE = 3.14 ms, TI = 900 ms, flip angle = 9°, iPAT = 2, partial Fourier = 6/8). Both T1w scans were visually inspected to ensure minimal head motion before they were submitted to further processing. qT1 relaxometry data were acquired using a 3D-MP2RAGE sequence (0.8 mm isotropic voxels, 240 sagittal slices, TR = 5000 ms, TE = 2.9 ms, TI 1 = 940 ms, T1 2 = 2830 ms, flip angle 1 = 4°, flip angle 2 = 5°, iPAT = 3, bandwidth = 270 Hz/px, echo spacing = 7.2 ms, partial Fourier = 6/8). We combined two inversion images for qT1 mapping in order to minimise sensitivity to B1 inhomogeneities and optimize intra- and inter-subject reliability58,59. A 2D spin-echo echo-planar imaging sequence with multi-band acceleration was used to obtain DWI data, consisting of three shells with b-values 300, 700, and 2000s/mm2 and 10, 40, and 90 diffusion weighting directions per shell, respectively (1.6 mm isotropic voxels, TR = 3500 ms, TE = 64.40 ms, flip angle = 90°, refocusing flip angle = 180°, FOV = 224 × 224 mm2, slice thickness = 1.6 mm, multi-band factor = 3, echo spacing = 0.76 ms). b0 images acquired in reverse phase encoding direction are also provided for distortion correction of DWI scans. One 7 min rs-fMRI scan was acquired using multiband accelerated 2D-BOLD echo-planar imaging (3 mm isotropic voxels, TR = 600 ms, TE = 30 ms, flip angle = 52°, FOV = 240 × 240 mm2, slice thickness = 3 mm, mb factor = 6, echo spacing = 0.54 ms). Participants were instructed to keep their eyes open, look at a fixation cross, and not fall asleep. We also include two spin-echo images with reverse phase encoding for distortion correction of the rs-fMRI scans (3 mm isotropic voxels, TR = 4029 ms, TE = 48 ms, flip angle = 90°, FOV = 240 × 240 mm2, slice thickness = 3 mm, echo spacing = 0.54 ms, phase encoding = AP/PA, bandwidth = 2084 Hz/Px). A complete list of acquisition parameters is provided in the detailed imaging protocol available alongside this data release.
MRI data pre-processing
Raw DICOMS were sorted by sequence, converted to NIfTI format using dcm2niix (v1.0.20200427; https://github.com/rordenlab/dcm2niix)60, renamed, and assigned to their respective subject-specific directories according to BIDS57. Agreement between the resulting data structure and BIDS standards was ascertained using the BIDS-validator (v1.5.10; https://doi.org/10.5281/zenodo.3762221)61. All further processing was performed via micapipe, an openly accessible processing pipeline for multimodal MRI data (https://micapipe.readthedocs.io/), and BrainSpace, a toolbox for macroscale gradient mapping (https://brainspace.readthedocs.io/)62.
T1w pre-processing
Native structural images were anonymized and de-identified by defacing all structural volumes using custom scripts (https://github.com/MICA-LAB/micapipe/; micapipe_anonymize). Note that processing derivatives were generated from non-anonymized images. Structural processing was carried out using several software packages, including tools from AFNI, FSL, and ANTs63. Each T1w scan was deobliqued and reoriented to standard neuroscience orientation (LPI: left to right, posterior to anterior, and inferior to superior). Both scans were then linearly co-registered and averaged, automatically corrected for intensity nonuniformity64, and intensity normalized. Resulting images were skull-stripped, and subcortical structures were segmented using FSL FIRST65. Cortical surface segmentations were generated from native T1w scans using FreeSurfer 6.066,67,68.
qT1 pre-processing
Native qT1 scans were anonymized and de-identified by defacing. For pre-processing, a series of equivolumetric surfaces were first constructed for each participant between pial and white matter boundaries. These surfaces were used for systematic sampling of qT1 image intensities from raw T1 maps (i.e., /rawdata/sub-HC#/ses-01/anat/*T1map.nii.gz), to compute individual microstructural profile similarity matrices6,7 (see next section). Here, qT1 images were co-registered to native FreeSurfer space of each participant using boundary-based registration69. No additional pre-processing was applied to qT1 images.
DWI pre-processing
DWI data were pre-processed using MRtrix70,71. DWI data was denoised72,73, underwent b0 intensity normalization64, and were corrected for susceptibility distortion, head motion, and eddy currents using a reverse phase encoding from two b = 0 s/mm2 volumes. Required anatomical features for tractography processing (e.g., tissue type segmentations, parcellations) were non-linearly co-registered to native DWI space using the deformable SyN approach implemented in ANTs74. Diffusion processing was performed in native DWI space.
rs-fMRI pre-processing
rs-fMRI images were pre-processed using AFNI75 and FSL65. The first five volumes were discarded to ensure magnetic field saturation. Images were reoriented, as well as motion and distortion corrected. Motion correction was performed by registering all timepoint volumes to the mean volume, while distortion correction leveraged main phase and reverse phase field maps acquired alongside rs-fMRI scans. Nuisance variable signal was removed using an ICA-FIX76 classifier trained in-house on a subset of 30 participants (15 healthy controls, 15 drug-resistant epilepsy patients) and by performing spike regression using motion outlier outputs provided by FSL. Volumetric timeseries were averaged for registration to native FreeSurfer space using boundary-based registration69, and mapped to individual surface models using trilinear interpolation. Native-surface cortical timeseries underwent spatial smoothing once mapped to each individual’s cortical surface models (Gaussian kernel, FWHM = 10 mm)77,78, and were subsequently averaged within nodes defined by several parcellation schemes (see below). Parcellated subcortical timeseries are also provided in this release and were appended before cortical timeseries. Subject-specific subcortical parcellations were non-linearly registered to each individual’s native fMRI space using the deformable SyN approach implemented in ANTs74.
Generating individual and group-level connectome matrices
The following sections describe the construction of feature matrices, derived from each imaging sequence included in this data release (Fig. 1b). Cortical connectomes are provided according to anatomical20, intrinsic functional24, and multimodal parcellation schemes26 at different resolutions, for a total of 18 distinct cortical parcellations. Anatomical atlases available in this dataset include Desikan-Killiany (aparc)20 and Destrieux (aparc.a2009s)21 parcellations provided by FreeSurfer, as well as an in vivo approximation of the cytoarchitectonic parcellation studies of Von Economo and Koskinas79. We additionally include similarly sized subparcellations, constrained within the boundaries of the Desikan-Killany atlas20, providing matrices with 100 to 400 cortical parcels following major sulco-gyral landmarks. Parcellations based on intrinsic functional activity (Schaefer atlases based on 7-network parcellation) are also included in this release according to a wide range of resolutions (100–1000 nodes)24. Lastly, we also provide connectome matrices generated from a multimodal atlas with 360 nodes derived from the Human Connectome Project dataset, known as the Glasser parcellation26. All atlases are available on Conte6980 and fsaverage5 surface templates (see parcellations in https://github.com/MICA-MNI/micapipe), and were resampled to each participant’s native surface to generate modality- and subject-specific matrices. In addition, structural and functional connectome matrices include data for each subcortical structure (nucleus accumbens, amygdala, caudate nucleus, pallidum, putamen, and thalamus) and the hippocampus appended before entries for cortical parcels (see Usage notes).
Geodesic distance (GD)
We computed individual GD matrices along each participant’s native cortical midsurface using workbench tools77,78. First, a centroid vertex was defined for each cortical parcel by identifying the vertex with the shortest summed Euclidean distance from all other vertices within its assigned parcel. The GD between centroid vertices and all other vertices on the native midsurface mesh was computed using Dijkstra’s algorithm. Notably, this implementation computes distances not only across vertices sharing a direct connection, but also across pairs of triangles which share an edge to mitigate the impact of mesh configuration on calculated distances. Vertex-wise GD values were averaged within parcels.
Microstructural profile covariance (MPC)
We generated 14 equivolumetric intracortical surfaces81 to sample qT1 intensities across cortical depths, yielding distinct intensity profiles reflecting the intracortical microstructural composition at each cortical vertex. This number of surfaces was selected based on recent stability analyses of resulting MPC matrices6,7. Data sampled from surfaces closest to the pial and white matter boundaries were discarded to mitigate partial volume effects. Vertex-wise intensity profiles were averaged within parcels. Nodal microstructural profiles were cross-correlated across the cortical mantle using partial correlations while controlling for the average cortex-wide intensity profile, and log-transformed6,7. Left and right medial walls, as well as non-cortical areas such as corpus callosum and peri-callosal regions of the Desikan-Killiany and Destrieux parcellations were excluded when averaging cortex-wide intensity profiles. Resulting matrices thus represented participant-specific similarity matrices in myelin proxies across the cortex.
Diffusion MRI tractography derived structural connectivity (SC)
Structural connectomes were generated with MRtrix from pre-processed DWI data70,71. We performed anatomically-constrained tractography using tissue types (cortical and subcortical grey matter, white matter, cerebrospinal fluid) segmented from each participant’s pre-processed T1w images registered to native DWI space82. We estimated multi-shell and multi-tissue response functions83 and performed constrained spherical-deconvolution and intensity normalization84. We generated a tractogram with 40 million streamlines (maximum tract length = 250; fractional anisotropy cutoff = 0.06). We applied spherical deconvolution informed filtering of tractograms (SIFT2) to reconstruct whole brain streamlines weighted by cross-sectional multipliers85. The reconstructed cross-section streamlines were mapped to each parcellation scheme (cortical and subcortical), which were also warped to DWI space. The connection weights between nodes were defined as the weighted streamline count.
Functional connectivity (FC)
Individual rs-fMRI timeseries mapped to subject-specific surface models were averaged within cortical parcels. The subcortical parcellation was warped to each subject’s native fMRI volume space and used to average timeseries within each node. Individual functional connectomes were generated by cross-correlating all nodal timeseries. For analyses presented in this paper, correlation values subsequently underwent Fisher-R-to-Z transformations. However, all FC matrices are provided as raw correlation matrices in the released data.
Data Records
All files are organized according to the Brain Imaging Directory Structure (BIDS)57 and are hosted on the Canadian Open Neuroscience Platform’s data portal (CONP; https://portal.conp.ca/dataset?id=projects/mica-mics). All data is also available via the Open Science Framework (OSF; https://osf.io/j532r/)86. Due to storage limitations on the OSF platform, derivative and raw data were uploaded in different project components, and raw data files were furthermore compressed into 5-subject batches.
Native space data
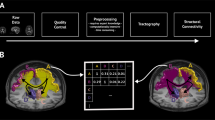
Native space data and corresponding.json files are contained in the branch /rawdata/sub-HC#/ses-01 of the directory structure (Fig. 2a). For each subject (/sub-HC#/ses-01), the /anat subdirectory includes several NIfTI files containing native space T1w and qT1 images. T1w scans are named according to acquisition order, denoted by run-#. For unprocessed qT1 images, we provide results of each inversion time parameter (denoted by inv-1 and inv-2), T1 mapping based on the combination of both inversion time images (T1-map), as well as MP2RAGE-derived synthetic T1w images (uni). Removal of facial features by masking was the only change applied to these images (see MRI data pre-processing).
Directory structure of MICA-MICs dataset. (a) Anonymized data with no additional processing are provided in the rawdata branch of the directory structure, and includes qT1, T1w, diffusion-weighted, and resting-state functional imaging data. (b) Processing derivatives are organized according to their associated pipelines. Group and subject-level gradients (/derivatives/gradients) were derived from averaged and individual connectivity matrices computed from several parcellation schemes using micapipe (/derivatives/micapipe). Matrices and gradients are organized into modality-specific directories for structural (/anat/micro_profiles for MPC, /anat/geo_dist for geodesic distance), functional (/func), and diffusion-weighted (/dwi) imaging. We additionally provide detailed image quality reports for T1w and rsfMRI raw data generated using MRIQC87.
Subject-specific DWI files can be found in the /rawdata/sub-HC#/ses-01/dwi subdirectory. Gradient direction, diffusion weighting, DWI volumes, and.json sidecar files are associated with each shell, indicated by its corresponding b-value and number of diffusion directions in the filename (e.g., “sub-HC#_ses-01_acq-b#_dir-AP_dwi.json”). b0 images are denoted by their inverse phase encoding direction (PA; i.e., “sub-HC#_ses-01_dir-PA_dwi.json”).
The rs-fMRI scans as well as associated spin-echo images used for distortion correction are located in the /rawdata/sub-HC#/ses-01/func subdirectory. Functional timeseries include 700 timepoints, with the exception of subject numbers equal to or preceding sub-HC004 who underwent slightly longer acquisition (800 timepoints). Phase encoding direction of spin-echo images are indicated in the filename (i.e., APse – anterior-posterior – or PAse – posterior-anterior. The string “se” following phase-encoding direction in the filename indicates a spin-echo image later used for distortion correction).
Processed data
Processed data included in this release are stored in the derivatives subdirectory associated with their processing pipeline (Fig. 2b). Quality control reports of raw structural and functional data are provided in derivatives/mriqc/. Modality-specific matrices of varying granularity (70–1000 nodes) were generated using micapipe, and are stored in their respective subdirectory (e.g., all functional connectomes can be found in derivatives/micapipe/sub-HC#/ses-01/func/). We also provide group- and subject-level gradients generated from each matrix, stored in derivatives/gradients/ses-01/ (see Technical validation and derivative metrics).
Structural processing
Surface-mapped processing derivatives of structural scans are provided in /derivatives/micapipe/sub-HC#/ses-01/anat. These features are organized in two distinct subdirectories. First, MPC matrices generated from processed qT1 scans are stored in the /micro_profiles subdirectory and are identified by the parcellation scheme from which they were computed (e.g., “sub-HC#_ses-01_space-fsnative_atlas-schaefer100_desc-mpc.txt”). GD matrices for each cortical parcellation scheme are included in the /geo_dist subdirectory (e.g., “sub-HC#_ses-01_space-fsnative_atlas-schaefer100_desc-gd.txt”). As described in a previous section, individual geodesic distance matrices were computed along each participant’s native midsurface using workbench77,78.
DWI processing
Processing derivatives of DWI scans are provided in /derivatives/micapipe/sub-HC#/ses-01/dwi. Structural connectomes (e.g., “sub-HC#_ses-01_space-dwinative_atlas-schaefer100_desc-sc.txt”) and associated edge lengths (e.g., “sub-HC#_ses-01_space-dwinative_atlas-schaefer100_desc-edgeLength.txt”) are provided for each parcellation.
rs-fMRI processing
Fully processed connectomes (i.e., after removal of nuisance variable signal using ICA-FIX76, mapping to native cortical surface, spatial smoothing, and regression of motion spikes) are provided in /derivatives/micapipe/sub-HC#/ses-01/func (e.g., “sub-HC#_ses-01_space-fsnative_atlas-schaefer100_desc-fc.txt”). Functional connectomes were computed from native-surface mapped timeseries for congruency across data modalities, as both GD and MPC matrices are generated from data mapped to native cortical surface models.
Quality control
Reports of image quality metrics computed by MRIQC v0.15.2 (https://github.com/poldracklab/mriqc/)87 are included in the /mriqc branch of MICA-MICs processing derivatives. For each subject, /mriqc directories contain /anat and /func subdirectories, which include image quality metric reports for T1w and resting-state functional scans in.html and.json formats. These reports provide a number of metrics evaluating the quality of the input data, including estimates of motion, signal-to-noise, and intensity non-uniformities87.
Technical Validation and Derivative Metrics
Quality control procedures
Cortical surface segmentations
Surface extractions were visually inspected by three authors (JR, AJL, CP) and corrected for any segmentation errors with the placement of control points and manual edits.
Image quality metrics
The consistency of T1w scan quality was assessed using contrast-to-noise estimates computed in MRIQC87 (Fig. 3a). This metric provides a measure of separability of grey and white matter distributions for a given T1w image87,88, with higher values indicating better image quality. For DWI scans, movement was quantified in each shell using MRtrix and FSL eddy, specifically using restricted movement root mean squared (RMS) outputs89 (Fig. 3b). For rs-fMRI, framewise displacement (FD) was estimated using FSL’s motion outlier detection tool. We also explored temporal signal-to-noise (tSNR) ratio, calculated for each participant by dividing surface-mapped mean timeseries by their standard deviation. Motion and distortion corrected timeseries were used to calculate tSNR across the cortex for each participant (i.e., before high-pass filtering and nuisance signal regression using ICA-FIX). Vertex-wise tSNR values were averaged within parcels to aggregate values across subjects (Fig. 3c).
Image quality metrics across sequences. (a) Contrast-to-noise (CNR), estimated with MRIQC87, showed no outliers in either T1w scan (first scan in blue, second scan in green). (b) Motion parameters of diffusion-weighted images were obtained from FSL eddy89. The histogram illustrates root mean squared (RMS) voxel-wise displacement relative to the first volume across all shells. Line plots show RMS displacement in each volume relative to the previous volume. (c) Framewise displacement (FD) of resting-state functional scans was obtained using FSL motion outliers, reflecting the average of rotation and translation parameter differences at each volume92. The histogram shows subjects-wise average FD across volumes. Line plots show FD across resting-state acquisitions for three participants, with respectively 20th, 50th, and 80th percentile average FD across our sample. Dashed line indicates 0.2 mean FD threshold used for exclusion of participants with excessive motion. Vertex-wise temporal signal-to-noise (tSNR) was calculated on the native surface of each participant. Computed tSNR values were averaged within a 400-node functional parcellation (Schaefer-400) and averaged across individuals.
Estimation of cortical gradients from MPC, FC, SC, and GD matrices
In this section, we demonstrate how group and individual-level gradients can be derived from each data modality provided in MICA-MICs. Using the BrainSpace toolbox (http://brainspace.readthedocs.io)62, we identified gradients from MPC, FC, SC, and GD matrices. We constructed group-level gradients by averaging all cortical entries of subject-level matrices constructed from the Schaefer-400 atlas. MPC, FC, and GD matrices were computed by cross-subject averaging, and results were thresholded row-wise to retain the top 10% edges, as in previous work7,14,32,35. Group-level structural connectivity (SC) was computed using distance-dependent thresholding to preserve the distribution of within- and between-hemisphere connection lengths in individual subjects90. Prior to averaging, subject-level SC matrices were log-transformed to reduce connectivity strength variance. Group-average SC matrices were thresholded to only retain positive edges. No further thresholding was applied given the sparsity of SC matrices relative to other modalities.
Normalized angle affinity matrices, capturing inter-regional similarity of microstructural, connectivity, and distance patterns, were computed from each modality-specific matrix (Fig. 4a, top). Left and right hemispheres were analysed separately for SC data, given limitations of diffusion tractography in mapping inter-hemispheric fibres. Hemispheres were also analysed separately for GD gradients, as the surface-based measure of geodesic distance used here is computed on distinct hemisphere surface spheres. Data from both hemispheres were used to generate affinity matrices from MPC and FC features. We applied diffusion map embedding, a non-linear dimensionality reduction technique14,62,91, to each affinity matrix to identify eigenvectors (or gradients) describing inter-regional variability in each feature in descending order for each modality (Fig. 4a, middle). Resulting gradients were visualized on cortical surfaces, revealing distinct patterns for each feature (Fig. 4a, bottom). For instance, the first MPC gradient (G1) derived from myelin-sensitive qT1 recapitulated a sensory-fugal axis44,45 ordering nodes from sensorimotor to paralimbic cortices7. In contrast, the principal FC and SC gradients primarily distinguished visual and sensorimotor cortices. The second gradient of FC, explaining a similar amount of variance to FC-G1, was anchored in unimodal sensory systems and the higher-order default mode network14. Gradients of geodesic distance highlighted the longest distance axes across the cortical surface mesh, specifically evolving along anterior to posterior (G1) and mesial/inferior to lateral/superior (G2) directions.
Deriving smooth microstructural, connectivity, and distance gradients. (a) Matrices derived from the Schaefer-400 parcellation describing (i) microstructural similarity, (ii) functional connectivity, (iii) structural connectivity, and (iv) spatial proximity were thresholded, and transformed into affinity matrices using a normalized angle kernel (top row). Only left hemisphere data is shown, although data from both hemispheres was included in MPC and FC analyses. We then applied diffusion map embedding, a non-linear dimensionality reduction technique, to each affinity matrix to derive gradients describing inter-regional variability in each feature in descending order (middle row). A subset of resulting gradients is projected onto the cortical surface for each modality (bottom row). (b) We assessed reproducibility of group-level gradient patterns at the individual-participant level using Spearman correlations. We generated gradients for each modality, in each participant, and aligned resulting eigenvectors to corresponding group-level gradient data. Box plots show variations in Spearman r-values across participants, for the first 10 gradients in each modality (presented in the same order as panel (a). Note change in y-axis scale in SC and GD box plots.
We next assess the reproducibility of group-average gradients in individual participants. Subject-level gradients were generated following the same procedure as previously described group-level analyses. Resulting subject-level gradients were aligned with group-level template gradients generated from the 49 other participants using Procrustes alignment62. This procedure (i.e., excluding a single participant from the template used for alignment) ensured that resulting correlations were not spuriously increased by correlating single-subject data present in both sets. Aligned subject-level gradients were correlated with their corresponding gradient in the group-level data (Fig. 4b). A similar pattern was seen across all modalities, with decreasing individual-level replicability in gradients explaining less variance within each feature. Indeed, G1 was highly reproducible in all participants across all modalities (r mean ± SD; MPC 0.785 ± 0.041; FC 0.839 ± 0.065; SC 0.973 ± 0.008; GD 0.989 ± 0.003), but correlations between individual subject data and group-level template gradients were lower for gradients explaining less variance (e.g., G10; MPC 0.193 ± 0.064; FC 0.416 ± 0.127; SC 0.785 ± 0.083; GD 0.940 ± 0.019).
All subject-level gradients provided in this release were aligned to the full group template, and are provided for each modality and parcellation scheme. As such, all individual-subject gradients are aligned to an identical template. These files are included in their respective /derivatives subdirectories. For instance, all FC gradients for a given participant can be found in the /derivatives/gradients/ses-01/subjects/sub-HC# subdirectory (e.g., “sub-HC#_ses-01_space-fsnative_atlas-schaefer100_desc-fcGradient.txt” for FC gradients). Gradients generated from the averaged full sample data can also be accessed within their respective /derivatives/gradients directories (e.g., /derivatives/gradients/ses-01/group/func for FC gradients).
Usage Notes
Data hosting
MICA-MICs is made openly available via the CONP portal (https://portal.conp.ca/dataset?id=projects/mica-mics) and OSF86 (https://osf.io/j532r/).
Matrix ordering
Rows and columns of GD and MPC matrices follow the order defined by annotation labels associated with their parcellation (see parcellations in https://github.com/MICA-LAB/micapipe), including unique entries for the left and right medial walls. For example, row and column entries of the Schaefer-100 matrices are ordered according to: Left hemisphere cortical parcels (1 medial wall followed by 50 cortical regions), and right hemisphere cortical parcels (1 medial wall followed by 50 cortical regions). FC and SC matrices follow the same ordering, although entries for subcortical structures are appended before cortical parcels. As such, row and column entries of the Schaefer-100 FC and SC matrices are ordered according to: Subcortical structures and hippocampus (7 left, 7 right), left hemisphere cortical parcels (1 medial wall followed by 50 cortical regions), and right hemisphere cortical parcels (1 medial wall followed by 50 cortical regions). The ordering of all parcels and their corresponding label in each volumetric parcellation are documented in lookup tables provided with our analysis pipeline.
Gradient data
Nodes excluded from group- and individual-level gradient analyses are indicated by a value of Inf in the corresponding node index. These data points may correspond to non-cortical nodes (e.g., medial wall, callosal or peri-callosal areas) or to nodes with no connections to other areas. This second case occasionally occurred in higher-resolution (>500 nodes) SC matrices of individual subjects.
Code availability
All processing pipeline scripts are openly available. Code used to generate pre-processed outputs can be accessed via GitHub (https://github.com/MICA-MNI/micapipe). Documentation for the processing pipeline, including usage and detailed processing steps, can also be accessed via ReadTheDocs (https://micapipe.readthedocs.io).
References
Lariviere, S. et al. Microstructure-informed connectomics: enriching large-scale descriptions of healthy and diseased brains. Brain connectivity 9, 113–127 (2019).
Sereno, M. I., Lutti, A., Weiskopf, N. & Dick, F. Mapping the human cortical surface by combining quantitative T 1 with retinotopy. Cerebral cortex 23, 2261–2268 (2013).
Nieuwenhuys, R. The myeloarchitectonic studies on the human cerebral cortex of the Vogt–Vogt school, and their significance for the interpretation of functional neuroimaging data. Brain Structure and Function 218, 303–352 (2013).
Vogt, C. & Vogt, O. in Nervensystem 448–477 (Springer, 1928).
Shams, Z., Norris, D. G. & Marques, J. P. A comparison of in vivo MRI based cortical myelin mapping using T1w/T2w and R1 mapping at 3T. PLoS One 14, e0218089 (2019).
Royer, J. et al. Myeloarchitecture gradients in the human insula: Histological underpinnings and association to intrinsic functional connectivity. Neuroimage 216, 116859 (2020).
Paquola, C. et al. Microstructural and functional gradients are increasingly dissociated in transmodal cortices. PLoS biology 17, e3000284 (2019).
Beul, S. F., Barbas, H. & Hilgetag, C. C. A predictive structural model of the primate connectome. Scientific reports 7, 1–12 (2017).
Barbas, H. & Rempel-Clower, N. Cortical structure predicts the pattern of corticocortical connections. Cerebral cortex (New York, NY: 1991) 7, 635–646 (1997).
Paquola, C. et al. A multi-scale cortical wiring space links cellular architecture and functional dynamics in the human brain. PLoS biology 18, e3000979 (2020).
Ecker, C. et al. Intrinsic gray-matter connectivity of the brain in adults with autism spectrum disorder. Proceedings of the National Academy of Sciences 110, 13222–13227 (2013).
Hong, S.-J., Valk, S. L., Di Martino, A., Milham, M. P. & Bernhardt, B. C. Multidimensional neuroanatomical subtyping of autism spectrum disorder. Cerebral Cortex 28, 3578–3588 (2018).
Schüz, A. & Braitenberg, V. The human cortical white matter: quantitative aspects of cortico-cortical long-range connectivity. Cortical areas: Unity and diversity, 377–385 (2002).
Margulies, D. S. et al. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proceedings of the National Academy of Sciences 113, 12574–12579 (2016).
Smallwood, J. et al. The default mode network in cognition: a topographical perspective. Nature reviews neuroscience 22, 503–513 (2021).
Wang, P. et al. Inversion of a large-scale circuit model reveals a cortical hierarchy in the dynamic resting human brain. Science advances 5, eaat7854 (2019).
Honey, C. J. et al. Predicting human resting-state functional connectivity from structural connectivity. Proceedings of the National Academy of Sciences 106, 2035–2040 (2009).
Park, H.-J. & Friston, K. Structural and functional brain networks: from connections to cognition. Science 342, 1238411 (2013).
Eickhoff, S. B., Yeo, B. & Genon, S. Imaging-based parcellations of the human brain. Nature Reviews Neuroscience 19, 672–686 (2018).
Desikan, R. S. et al. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 31, 968–980 (2006).
Destrieux, C., Fischl, B., Dale, A. & Halgren, E. Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. Neuroimage 53, 1–15 (2010).
von Economo, C. F. & Koskinas, G. N. Die cytoarchitektonik der hirnrinde des erwachsenen menschen. (J. Springer, 1925).
Brodmann, K. Vergleichende Lokalisationslehre der Grosshirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues. (Barth, 1909).
Schaefer, A. et al. Local-global parcellation of the human cerebral cortex from intrinsic functional connectivity MRI. Cerebral cortex 28, 3095–3114 (2018).
Fan, L. et al. The human brainnetome atlas: a new brain atlas based on connectional architecture. Cerebral cortex 26, 3508–3526 (2016).
Glasser, M. F. et al. A multi-modal parcellation of human cerebral cortex. Nature 536, 171–178 (2016).
Sporns, O., Tononi, G. & Kötter, R. The human connectome: a structural description of the human brain. PLoS computational biology 1, e42 (2005).
Biswal, B., Yetkin, F. Z., Haughton, V. M. & Hyde, J. S. Functional connectivity in the motor cortex of resting human brain using echo‐planar MRI. Magnetic resonance in medicine 34, 537–541 (1995).
Yeo, B. T. et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. Journal of neurophysiology (2011).
Przeździk, I., Faber, M., Fernández, G., Beckmann, C. F. & Haak, K. V. The functional organisation of the hippocampus along its long axis is gradual and predicts recollection. Cortex 119, 324–335 (2019).
Haak, K. V., Marquand, A. F. & Beckmann, C. F. Connectopic mapping with resting-state fMRI. Neuroimage 170, 83–94 (2018).
Larivière, S. et al. Multiscale structure–function gradients in the neonatal connectome. Cerebral Cortex 30, 47–58 (2020).
Marquand, A. F., Haak, K. V. & Beckmann, C. F. Functional corticostriatal connection topographies predict goal-directed behaviour in humans. Nature human behaviour 1, 1–9 (2017).
Guell, X., Schmahmann, J. D., Gabrieli, J. D. & Ghosh, S. S. Functional gradients of the cerebellum. Elife 7, e36652 (2018).
Vos de Wael, R. et al. Anatomical and microstructural determinants of hippocampal subfield functional connectome embedding. Proceedings of the National Academy of Sciences 115, 10154–10159 (2018).
Cerliani, L. et al. Probabilistic tractography recovers a rostrocaudal trajectory of connectivity variability in the human insular cortex. Human brain mapping 33, 2005–2034 (2012).
Bajada, C. J. et al. A graded tractographic parcellation of the temporal lobe. Neuroimage 155, 503–512 (2017).
Park, B.-y et al. Signal diffusion along connectome gradients and inter-hub routing differentially contribute to dynamic human brain function. Neuroimage 224, 117429 (2021).
Paquola, C. et al. Shifts in myeloarchitecture characterise adolescent development of cortical gradients. Elife 8, e50482 (2019).
Valk, S. L. et al. Shaping brain structure: Genetic and phylogenetic axes of macroscale organization of cortical thickness. Science Advances 6, eabb3417 (2020).
Paquola, C. et al. Convergence of cortical types and functional motifs in the human mesiotemporal lobe. Elife 9, e60673 (2020).
Vogel, J. W. et al. A molecular gradient along the longitudinal axis of the human hippocampus informs large-scale behavioral systems. Nature communications 11, 1–17 (2020).
Burt, J. B. et al. Hierarchy of transcriptomic specialization across human cortex captured by structural neuroimaging topography. Nature Neuroscience 21, 1251–1259, https://doi.org/10.1038/s41593-018-0195-0 (2018).
Mesulam, M.-M. From sensation to cognition. Brain: a journal of neurology 121, 1013–1052 (1998).
Mesulam, M. M. in Principles of behavioral and cognitive neurology, 2nd ed. 1–120 (Oxford University Press, 2000).
Van Essen, D. C. et al. The WU-Minn human connectome project: an overview. Neuroimage 80, 62–79 (2013).
Miller, K. L. et al. Multimodal population brain imaging in the UK Biobank prospective epidemiological study. Nature neuroscience 19, 1523–1536 (2016).
Kiddle, B. et al. Cohort profile: the NSPN 2400 Cohort: a developmental sample supporting the Wellcome Trust NeuroScience in Psychiatry Network. International journal of epidemiology 47, 18–19g (2018).
Avesani, P. et al. The open diffusion data derivatives, brain data upcycling via integrated publishing of derivatives and reproducible open cloud services. Scientific Data 6, 69, https://doi.org/10.1038/s41597-019-0073-y (2019).
Taylor, J. R. et al. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository: Structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. Neuroimage 144, 262–269 (2017).
Di Martino, A. et al. Enhancing studies of the connectome in autism using the autism brain imaging data exchange II. Scientific Data 4, 170010, https://doi.org/10.1038/sdata.2017.10 (2017).
Di Martino, A. et al. The autism brain imaging data exchange: towards a large-scale evaluation of the intrinsic brain architecture in autism. Molecular Psychiatry 19, 659–667, https://doi.org/10.1038/mp.2013.78 (2014).
Markiewicz, C. J. et al. The OpenNeuro resource for sharing of neuroscience data. Elife 10, e71774 (2021).
Gorgolewski, K. J. et al. BIDS apps: Improving ease of use, accessibility, and reproducibility of neuroimaging data analysis methods. PLoS computational biology 13, e1005209 (2017).
Harding, R. J. et al. The Canadian Open Neuroscience Platform–An Open Science Framework for the Neuroscience Community. (2022).
Milham, M. P. et al. Assessment of the impact of shared brain imaging data on the scientific literature. Nature Communications 9, 1–7 (2018).
Gorgolewski, K. J. et al. The brain imaging data structure, a format for organizing and describing outputs of neuroimaging experiments. Scientific data 3, 1–9 (2016).
Haast, R. A., Ivanov, D. & Formisano, E. & Uludaǧ, K. Reproducibility and reliability of quantitative and weighted T1 and T2∗ mapping for myelin-based cortical parcellation at 7 Tesla. Frontiers in neuroanatomy 10, 112 (2016).
Marques, J. P. et al. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. Neuroimage 49, 1271–1281 (2010).
Li, X., Morgan, P. S., Ashburner, J., Smith, J. & Rorden, C. The first step for neuroimaging data analysis: DICOM to NIfTI conversion. Journal of neuroscience methods 264, 47–56 (2016).
Blair, R. bids-validator. Zenodo https://doi.org/10.5281/zenodo.4473249 (2021).
Vos de Wael, R. et al. BrainSpace: a toolbox for the analysis of macroscale gradients in neuroimaging and connectomics datasets. Communications biology 3, 1–10 (2020).
Tustison, N. J. Explicit B-spline regularization in diffeomorphic image registration. Frontiers in neuroinformatics 7, 39 (2013).
Tustison, N. J. et al. N4ITK: improved N3 bias correction. IEEE transactions on medical imaging 29, 1310–1320 (2010).
Jenkinson, M., Beckmann, C. F., Behrens, T. E. & Woolrich, M. W. & Smith, S. M. Fsl. Neuroimage 62, 782–790 (2012).
Fischl, B., Sereno, M. I., Tootell, R. B. & Dale, A. M. High‐resolution intersubject averaging and a coordinate system for the cortical surface. Human brain mapping 8, 272–284 (1999).
Fischl, B., Sereno, M. I. & Dale, A. M. Cortical surface-based analysis: II: inflation, flattening, and a surface-based coordinate system. Neuroimage 9, 195–207 (1999).
Dale, A. M., Fischl, B. & Sereno, M. I. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage 9, 179–194 (1999).
Greve, D. N. & Fischl, B. Accurate and robust brain image alignment using boundary-based registration. Neuroimage 48, 63–72 (2009).
Tournier, J.-D. et al. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. Neuroimage 202, 116137 (2019).
Tournier, J. D., Calamante, F. & Connelly, A. MRtrix: diffusion tractography in crossing fiber regions. International journal of imaging systems and technology 22, 53–66 (2012).
Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. Neuroimage 142, 394–406 (2016).
Cordero-Grande, L., Christiaens, D., Hutter, J., Price, A. N. & Hajnal, J. V. Complex diffusion-weighted image estimation via matrix recovery under general noise models. Neuroimage 200, 391–404 (2019).
Avants, B. B., Epstein, C. L., Grossman, M. & Gee, J. C. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Medical image analysis 12, 26–41 (2008).
Cox, R. W. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Computers and Biomedical research 29, 162–173 (1996).
Salimi-Khorshidi, G. et al. Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90, 449–468 (2014).
Glasser, M. F. et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124 (2013).
Marcus, D. et al. Informatics and data mining tools and strategies for the human connectome project. Frontiers in neuroinformatics 5, 4 (2011).
Scholtens, L. H., de Reus, M. A., de Lange, S. C., Schmidt, R. & van den Heuvel, M. P. An mri von economo–koskinas atlas. NeuroImage 170, 249–256 (2018).
Van Essen, D. C., Glasser, M. F., Dierker, D. L., Harwell, J. & Coalson, T. Parcellations and hemispheric asymmetries of human cerebral cortex analyzed on surface-based atlases. Cerebral cortex 22, 2241–2262 (2012).
Waehnert, M. et al. Anatomically motivated modeling of cortical laminae. Neuroimage 93, 210–220 (2014).
Smith, R. E., Tournier, J.-D., Calamante, F. & Connelly, A. Anatomically-constrained tractography: improved diffusion MRI streamlines tractography through effective use of anatomical information. Neuroimage 62, 1924–1938 (2012).
Christiaens, D. et al. Global tractography of multi-shell diffusion-weighted imaging data using a multi-tissue model. Neuroimage 123, 89–101 (2015).
Jeurissen, B., Tournier, J.-D., Dhollander, T., Connelly, A. & Sijbers, J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage 103, 411–426 (2014).
Smith, R. E., Tournier, J.-D., Calamante, F. & Connelly, A. SIFT2: Enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography. Neuroimage 119, 338–351 (2015).
Royer, J. et al. MICA-MICs: a dataset for Microstructure-Informed Connectomics. Open Science Framework https://doi.org/10.17605/OSF.IO/J532R (2021).
Esteban, O. et al. MRIQC: Advancing the automatic prediction of image quality in MRI from unseen sites. PloS one 12, e0184661 (2017).
Magnotta, V. A. & Friedman, L. Measurement of signal-to-noise and contrast-to-noise in the fBIRN multicenter imaging study. Journal of digital imaging 19, 140–147 (2006).
Andersson, J. L. & Sotiropoulos, S. N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063–1078 (2016).
Betzel, R. F., Griffa, A., Hagmann, P. & Mišić, B. Distance-dependent consensus thresholds for generating group-representative structural brain networks. Network neuroscience 3, 475–496 (2019).
Coifman, R. R. et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Multiscale methods. Proceedings of the National Academy of Sciences 102, 7432–7437 (2005).
Power, J. D., Barnes, K. A., Snyder, A. Z., Schlaggar, B. L. & Petersen, S. E. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage 59, 2142–2154 (2012).
Acknowledgements
The authors wish to thank all participants who took part in this study. We also thank David Costa, Ronald Lopez, and Louise Marcotte for their assistance in data collection, as well as Ilana Leppert and Michael Ferreira for their guidance in designing the scanning protocol. This project has been made possible by the Brain Canada Foundation, through the Canada Brain Research Fund, with the financial support of Health Canada and its sponsors. JR received support from the Canadian Open Neuroscience Platform (CONP) and Canadian Institute of Health Research (CIHR). CP and RRC received support from the Fonds de la Recherche du Québec – Santé (FRQ-S). PH was supported by funding from the Canada First Research Excellence Fund, awarded to McGill University for the Healthy Brains for Healthy Lives initiative, the National Institutes of Health (NIH) NIH-NIBIB P41 EB019936 (ReproNim), the National Institute Of Mental Health of the NIH under Award Number R01MH096906, a research scholar award from Brain Canada, in partnership with Health Canada, for the CONP initiative, as well as an Excellence Scholarship from Unifying Neuroscience and Artificial Intelligence - Québec. ST received a Faculty of Medicine studentship from McGill University. QL received support from the China Scholarship Council. SL acknowledges funding from CIHR. RV received support from the Savoy Foundation and the Richard and Ann Sievers award. OB received support from the Healthy Brains for Healthy Lives (HBHL) program. RRC was supported by FRQ-S. BP was funded by the National Research Foundation of Korea (NRF-2021R1F1A1052303; NRF-2022R1A5A7033499), Institute for Information and Communications Technology Planning and Evaluation (IITP) funded by the Korea Government (MSIT) (No. 2022-0-00448, Deep Total Recall: Continual Learning for Human-Like Recall of Artificial Neural Networks; No. 2020-0-01389, Artificial Intelligence Convergence Research Center (Inha University); No. RS-2022-00155915, Artificial Intelligence Convergence Innovation Human Resources Development (Inha University); No. 2021-0-02068, Artificial Intelligence Innovation Hub), and Institute for Basic Science (IBS-R015-D1). BF receives salary support from FRQ-S (Chercheur-Boursier clinician Senior). BCB acknowledges support from CIHR (FDN-154298), SickKids Foundation (NI17-039), Natural Sciences and Engineering Research Council (NSERC; Discovery-1304413), Azrieli Center for Autism Research of the Montreal Neurological Institute (ACAR), BrainCanada, FRQ-S, and the Canada Research Chairs Program.
Author information
Authors and Affiliations
Contributions
Conception, design, and manuscript preparation: J.R., B.C.B.; Participant recruitment: J.R., S.T.; Data acquisition: Q.L., A.J.L., J.R., S.T.; Processing pipeline: P.H., S.L., C.P., B.P., J.R., R.R.C., R.V.; Data processing and quality control: S.L., Q.L., J.R., R.R.C., S.T., R.V. All authors provided feedback and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Royer, J., Rodríguez-Cruces, R., Tavakol, S. et al. An Open MRI Dataset For Multiscale Neuroscience. Sci Data 9, 569 (2022). https://doi.org/10.1038/s41597-022-01682-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-022-01682-y
This article is cited by
-
Open datasets and code for multi-scale relations on structure, function and neuro-genetics in the human brain
Scientific Data (2024)
-
Sex differences in functional cortical organization reflect differences in network topology rather than cortical morphometry
Nature Communications (2024)
-
Gradients of Brain Organization: Smooth Sailing from Methods Development to User Community
Neuroinformatics (2024)
-
Multivariate information theory uncovers synergistic subsystems of the human cerebral cortex
Communications Biology (2023)