Abstract
Shedding light on the distribution and ecosystem function of mesopelagic communities in the twilight zone (~200–1000 m depth) of global oceans can bridge the gap in estimates of species biomass, trophic linkages, and carbon sequestration role. Ocean basin-scale bioacoustic data from ships of opportunity programs are increasingly improving this situation by providing spatio-temporal calibrated acoustic snapshots of mesopelagic communities that can mutually complement established global ecosystem, carbon, and biogeochemical models. This data descriptor provides an overview of such bioacoustic data from Australia’s Integrated Marine Observing System (IMOS) Ships of Opportunity (SOOP) Bioacoustics sub-Facility. Until 30 September 2020, more than 600,000 km of data from 22 platforms were processed and made available to a publicly accessible Australian Ocean Data Network (AODN) Portal. Approximately 67% of total data holdings were collected by 13 commercial fishing vessels, fostering collaborations between researchers and ocean industry. IMOS Bioacoustics sub-Facility offers the prospect of acquiring new data, improved insights, and delving into new research challenges for investigating status and trend of mesopelagic ecosystems.
Measurement(s) | bioacoustic data • sound quality |
Technology Type(s) | echosounder • data processing software |
Sample Characteristic - Organism | macro-zooplankton • micronekton |
Sample Characteristic - Environment | ocean |
Sample Characteristic - Location | Tasman Sea • Southern Ocean • Indian Ocean • South Pacific Ocean • North Pacific Ocean • Coral Sea • North Atlantic Ocean |
Machine-accessible metadata file describing the reported data: https://doi.org/10.6084/m9.figshare.13172516
Similar content being viewed by others
Background & Summary
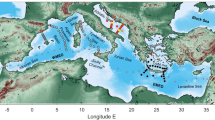
Since 2010, as a part of existing ocean industry collaboration, Australia’s Integrated Marine Observing System (IMOS) Ships of Opportunity (SOOP) Bioacoustics sub-Facility (here onwards IMOS Bioacoustics sub-Facility) has been collecting opportunistic, supervised, and unsupervised active bioacoustic data from different platforms including commercial fishing and research vessels transiting ocean basins1 (Fig. 1). The resulting acoustic snapshots2 provide a proxy for the combined effects of size, abundance, distribution, diversity, and behavior of mid-trophic mesopelagic communities including macro-zooplankton and micronekton in the twilight zone of global oceans (Fig. 2). The broad goal of IMOS Bioacoustics sub-Facility is to provide repeated active bioacoustic observations for the status and trend of ocean life to 1000 m at basin and decadal scales.
Schematic overview of IMOS Bioacoustics sub-Facility operations to collect and publish bioacoustic data with related metadata. Bioacoustic data received from diverse operators are quality-controlled and made available through the Australian Ocean Data Network (AODN) Portal. IMOS currently has a portfolio of 13 Facilities that undertake systematic and sustained observations of Australia’s marine environment. It is integrated in terms of its geographic domain (from coast to open ocean) and scientific domain, combining a wide range of physical, chemical, and biological observations from a variety of platforms. IMOS observations are turned into data that can be discovered, accessed, downloaded, used, and reused through the data Facility AODN.
The primary data-type derived from IMOS Bioacoustics sub-Facility is the georeferenced, calibrated3,4, and processed5 single-beam water column volume backscattering coefficient sv (m2 m−3) values, representing the linear sum of backscatter from acoustically detectable individual organisms within the sampling volume2 (Fig. 2). In suitable circumstances, it is proportional to the density of dominant scattering organisms, and the primary data for estimating biomass from acoustics at regional and global scales using existing6,7 and future methods.
Mesopelagic communities are mid-water predators and prey in the twilight zone, and presumed to make the largest natural daily animal movement on earth based on their biomass, revealing diel vertical migration8,9 and large-scale spatio-temporal patterns in pelagic sound scattering layers10 (Fig. 2). They have been identified as one of the least investigated components of open ocean ecosystems11, transferring energy from primary producers to higher predators, and regulating carbon transfer from surface to deep-ocean by linking epipelagic and deep-water food chains12,13,14,15,16.
Ships of opportunity bioacoustic sampling methods are useful for cost-effective mapping and biomass estimation of mesopelagic communities at regional and global scales with recognized potentials and challenges1. Acoustic estimation of biomass using vessel-based echosounder is complicated by many confounding factors17 including lack of accurate taxonomic information about insonified organisms, complex size distribution of scattering organisms, unknown species composition, and frequency-specific selectivity of echosounder measurements18,19. From an integrated ocean observing system perspective, a way forward to address these challenges would be to acquire multi-frequency data20,21 for improved segregation of dominant scattering groups. With advancing and diverse applications of multi-frequency systems, acoustic methods have been used to classify dominant organisms into gas-filled or fluid-filled categories22,23,24,25,26,27,28,29. Such methodologies are improving with the availability of broadband and wideband echosounders30 that would help to segment and attribute basin-scale bioacoustic observations into different scattering (or functional) groups.
Despite uncertainties with echosounder calibration, methodological challenges, species identification, and frequency-specific scattering of individual organisms, ships of opportunity bioacoustic sampling methods offer great potential to better understand the structure and ecosystem function of global mesopelagic communities, necessitating continued data acquisition and processing efforts5,31,32 with increased global accessibility33. The acoustic snapshots revealing spatio-temporal sound scattering patterns, deep scattering layer, and diel vertical migration (Fig. 2) can offer improved ecological insights34,35 for marine ecosystem acoustics36,37,38, in addition to established linkages with oceanographic processes39,40,41,42,43,44,45,46,47,48 and environmental covariates49,50,51 including light52,53,54, oxygen concentration55,56,57, temperature58,59, chlorophyll a60, and primary production6,59.
Currently, 22 platforms have contributed data to IMOS Bioacoustics sub-Facility, including both commercial fishing and research vessels (Table 1). Key time series data sets have been collected across the Tasman Sea, Southern Ocean, and Southern Indian Ocean. The extent of processed bioacoustic data archived under this sub-Facility is expanding with an improved spatial (Fig. 3) and temporal coverage (Fig. 4, until 30 September 2020). The majority of archived data are single-frequency 38 kHz (565,661 km) echosounder observations, but also include growing coverage of multi-frequency 18 kHz (118,260 km), 70 kHz (44,368 km), and 120 kHz (70,400 km) data, highlighting different scattering layers and functional groups.
Map showing spatial coverage of bioacoustic data processed until 30 September 2020. Fishing and research vessels are categorized as blue and magenta respectively. A satellite-derived map of ocean net primary production (NPP) averaged for the years 2009–2019 is superimposed. Readers are directed to check the AODN Portal for the latest data set.
The main goals and potential uptake values of IMOS Bioacoustics sub-Facility data are: (1) provide calibrated time series acoustic observations for the status and trend of mesopelagic ecosystem, (2) develop a framework synergizing active bioacoustic observations and ecosystem models61,62 for studying open ocean ecosystem dynamics, and (3) develop an active bioacoustic data-based ecosystem Essential Ocean Variable (eEOV)63 to complement established and future ocean observing systems measuring physical, chemical, and biological environment of the ocean. These frameworks would help to advance scientific knowledge of marine food chains and manage marine ecosystems sustainably.
Methods
The terminology used in this data descriptor follows Demer, et al.3, based mostly on Maclennan, et al.64. All symbols signifying variables are italicized. Any symbol for a variable (x) that is not logarithmically transformed is in lower case. Any symbol for a logarithmically transformed variable, e.g. \(X=1{0\log }_{10}\left(x/{x}_{ref}\right)\), with units of decibels referred to xref (dB re xref) is capitalized.
Echosounder data
In a widely used Simrad echosounder (Table 1), the proprietary format raw data (.raw) from each transmission and reception cycle (here onwards ping) includes received echo power per (W), with the General Purpose Transceiver (GPT) settings: frequency f (kHz), transmit power pet (W), pulse duration \(\tau \) (s), transducer on-axis gain G0 (dB re 1), area backscattering coefficient sa (m2 m–2) correction factor Sa corr (dB re 1), and equivalent two-way beam angle Ψ (dB re 1 sr) of the transducer. These data and associated settings were used to calculate and display volume backscattering strength \({S}_{v}\) (dB re 1 m2 m−3) for one or more frequency channels as3:
where \({P}_{er}\) (dB re 1 W) is the received power, \(r\) (m) is the range to the target, \({\alpha }_{a}\) (dB m–1) is the absorption coefficient, \(\lambda \) (m) is the wavelength, \({g}_{0}\) (dimensionless) is the transducer on-axis gain, \({c}_{w}\) (m s–1) is the sound speed in water, \(\psi \) (sr) is the equivalent two-way beam angle, and the index i and j represent vertical sample number and horizontal ping number respectively.
Echosounder calibration
Echosounder calibration is a prerequisite for quantitative bioacoustic studies. The overall on-axis performance of echosounders installed on the participating platforms was routinely evaluated by established sphere calibration method3,4. This method provides calibrated \({G}_{0}\) and \({S}_{a{\rm{c}}{\rm{o}}{\rm{r}}{\rm{r}}}\) required for standardizing \({S}_{v}\) data (Eq. 1) collected by diverse platforms with a traceable calibration history. The sphere calibration also provides a check for transducer beam-pattern characteristics and related Ψ. The manufacturer-specified Ψ adjusting for the local sound speed variation at the calibration location was used due to the difficulty in obtaining an independent measurement of hull-mounted transducer beam pattern.
The raw data acquired using ES60 and ES70 echosounders were modulated with a triangle wave error sequence65. The triangle wave error (with a 1 dB peak-to-peak amplitude and a 2720 ping period) was removed from calibration data before calculating \({G}_{0}\) and \({S}_{a{\rm{c}}{\rm{o}}{\rm{r}}{\rm{r}}}\). Open ocean transit (here onwards transect) data were not corrected for the triangle wave error due to data management and storage constraints at the start of the program. Generally, this error will average to zero over a full period of 2720 pings for normal operations and 1 km horizontal resolution of the processed data. To facilitate the processing of high-resolution data (e.g. 100 m horizontal resolution) and slow ping rate systems, transect data files were corrected for this error (if applicable) with associated metadata, since September 2020.
Data acquisition
Ensuring the operational need of participating platforms (e.g. fishing), the data acquisition settings in Table 2 were used to optimize quality and practical utility of collected data. The transmit power was selected based on the recommended20 settings for commonly used Simrad echosounders. The pulse duration was chosen as a trade-off between sample resolution and acceptable signal-to-noise ratio (SNR, dB re 1) in the mesopelagic zone, and the logging range was set to provide robust estimates of echosounder background noise (dB re 1 W) levels66.
Data registration and management
Depending on the primary purpose of participating platforms, raw data received from operators (Table 1) may cover transects and periods of fishing or scientific activities. A custom Java software suite was developed to assist data management and help identify transects for post processing (Fig. 5). These tools were used to create information (inf) files. The inf file is in plain text format that contains user-defined metadata (platform name, relevant platform call sign, voyage name, transect attributes, and relevant comments). It also includes key data acquisition settings extracted from the raw data files including frequency, transmit power, pulse duration, and echosounder details (GPT channel identifier and transducer model). The platform navigation details (total travel time, total distance covered, and average platform speed), temporal extent (start and end time of data volume), and geographic extent (limits of latitude and longitude) were also captured in the inf files. These inf files were checked for consistent data acquisition settings, transect selection, and excluding continental shelf water column backscatter data. Raw data files with inconsistent data acquisition or unknown calibration settings were not considered for further processing and archived locally.
Flowchart of methods implemented to produce quality-controlled bioacoustic data, providing an overview of data processing sequences in the context of key data variables present in a NetCDF file. Note that before transducer motion correction and filtering steps, calibrated \({S}_{v}\) values within each ping were resampled (by taking mean in the linear domain) to a specified vertical resolution of 2 m to smooth out vertical sample-to-sample variations in \({S}_{v}\).
Data processing routines
Data sets were initially processed using Echoview® software (Echoview Software Pty Ltd, Hobart, Tasmania, Australia) that includes a sequence of data processing filters5 designed to remove noise and improve data quality. Transect data files applying related time offset to Coordinated Universal Time (UTC) and calibration parameters were visualized (Eq. 1) as frequency-specific echograms in Echoview® for visual inspection, transducer motion correction, and filtering processes (Fig. 5). Subsequent processing and packaging were completed using MATLAB® software (MathWorks, Natick, Massachusetts, USA). All processing steps were semi-automated using a custom MATLAB® Graphical User Interface (GUI) integrated with Component Object Model (COM) objects controlling Echoview® software.
Visual inspection of data
Acoustic data quality from different platforms can vary significantly due to signal attenuation (i.e. attenuation of transmit and/or received signal to a level below the analysis threshold), and signal degradation due to combined transducer motion and noise. Data quality control involved visual inspection of echograms (Fig. 5), followed by marking the seabed (if present) and regions of bad data using echogram tools available in Echoview®. Pings with prolonged noise interference or signal attenuation were flagged as bad data. Data shallower than 10 m were removed to exclude echosounder transmit pulse and echoes in the transducer nearfield. Similarly, data deeper than the seabed (if present) were removed from the analyses. Additionally, regions of aliased seabed echoes (i.e. seabed reverberations from preceding pings coinciding with the current ping) were manually flagged as bad data. Valid high scattering from biological sources (e.g. pelagic fish schools that may occur between surface and 250 m depth) causing an apparent transition in backscatter intensities was manually preserved from the transient noise filter described below5.
Transducer motion correction
Echo-integration results will be biased if the change in orientation of transducer beam between the times of each ping is not accounted for. The effect of transducer motion on echo-integration was studied by Stanton67 and later Dunford68 developed a single correction function that can be applied for a wide range of circular transducers and related \({s}_{v}\) data. To fully characterize platform movement, the Dunford68 algorithm implemented in Echoview® requires motion data (i.e. pitch and roll of a platform) recorded at a rate above the Nyquist rate of platform’s angular motion69 to avoid temporal aliasing due to an inadequate sampling rate. When platform motion data were available at a suitable sampling rate (see ‘Technical Validation’ section), transducer motion effects were corrected using Dunford68 algorithm by ensuring time synchronization with recorded acoustic data (Fig. 5).
Data processing filters
Fishing vessels (FV) contributing to IMOS Bioacoustics sub-Facility were not purposely built for collecting high-quality bioacoustic data. Various factors including inclement weather and vessel design can affect data quality that could cause large biases in derived \({s}_{v}\) values. To minimize these biases, data processing filters were applied to the raw data (Fig. 5). Transducer motion-corrected data were subject to a sequence of data processing filters5 designed to mitigate impulse noise, signal attenuation, transient noise, and background noise66.
Data processing filters were applied to each \({S}_{v}\) sample in an echogram, identified by a vertical sample number \(i\) and horizontal ping number \(j\). The ‘context window’ defined for filters include a current ping, and surrounding pings on either side of the current ping. Depending on the filter used, the context window either centres on the current ping or current sample, and slides over the entire echogram.
Impulse noise removal
Impulse noise affects discrete sections of the data with a duration of less than one ping, for example, transmit pulses originated from other unsynchronized acoustic systems. The impulse noise removal algorithm implemented in Echoview® (based on Ryan, et al.5) compares each \({S}_{v}\) sample in a current ping to the adjacent \({S}_{v}\) samples (at the same depth) in surrounding pings defined by a context window of specified width \(W\) (see details of context window in Table 3). A smoothed copy of original \({S}_{v}\) values (i.e. unfiltered data) within the context window was used to identify impulse noise (see details of smoothing window in Table 3). The original \({S}_{v}\) samples were identified as impulse noise if the corresponding smoothed \({S}_{v}\) samples satisfy the condition:
where \({S}_{v}[i,j]\) (dB re 1 m2 m−3) represents smoothed copy of current ping with a vertical sample number \(i\) and horizontal ping number \(j\), \(m\) and \(n\) are the positive integer offsets from the current ping determined by the width (\(W\)) of context window, where \(m,n\in \left\{1,\ldots ,\frac{W-1}{2}\right\}\) and \(W\) is an odd integer value in the range 3 to 9, and \(\delta \) (dB re 1 m2 m−3) is an empirically determined impulse noise removal threshold value. Identified noise values were replaced as ‘no data’. The impulse noise removal parameters defined in Echoview® are given in Table 3.
Attenuated signal removal
Signal attenuation is generally caused by air bubbles beneath the transducer that may occur for one ping or can persist over multiple pings. The attenuated signal removal algorithm implemented in Echoview® (based on Ryan, et al.5) compares the percentile score of \({S}_{v}\) samples in a current ping with the percentile score of \({S}_{v}\) samples in surrounding pings defined by a context window (see details of context window in Table 4). The current ping was removed and replaced as ‘no data’ if:
where the symbol \(p\) denotes the desired percentile value, \({S}_{v}[i,j]\) (dB re 1 m2 m−3) is the current ping with a vertical sample number \(i\) and horizontal ping number \(j\), \({S}_{v}\left[m\times n\right]\) (dB re 1 m2 m−3) represents \({S}_{v}\) samples in the context window defined by \(m\) vertical samples and \(n\) horizontal pings, and \(\delta \) (dB re 1 m2 m−3) is an empirically determined attenuated signal removal threshold value. The attenuated signal removal parameters defined in Echoview® are given in Table 4.
Transient noise removal
Transient noise is introduced to the received signal that can occur at irregular intervals and persists over multiple pings. The transient noise removal algorithm implemented in Echoview® (based on Ryan, et al.5) compares each \({S}_{v}\) sample in a current ping with the percentile score of \({S}_{v}\) samples in surrounding pings defined by a context window (see details of context window in Table 5). A smoothed copy of original \({S}_{v}\) values (i.e. unfiltered data) within the context window was used to identify noise (see details of smoothing window in Table 5). The original \({S}_{v}\) samples were identified as transient noise if the corresponding smoothed \({S}_{v}\) samples satisfy the condition:
where the symbol \(p\) denotes the desired percentile value, \({S}_{v}[i,j]\) (dB re 1 m2 m−3) represents smoothed copy of current ping with a vertical sample number \(i\) and horizontal ping number \(j\), \({S}_{v}\left[m\times n\right]\) (dB re 1 m2 m−3) represents smoothed copy of \({S}_{v}\) samples in the context window defined by \(m\) vertical samples and \(n\) horizontal pings, and \(\delta \) (dB re 1 m2 m−3) is an empirically determined transient noise removal threshold value. Identified noise values were replaced as ‘no data’. The transient noise removal parameters defined in Echoview® are given in Table 5.
Background noise removal
Background noise is introduced to the received signal that can vary in intensity and pattern (see section ‘Technical Validation’). According to De Robertis and Higginbottom66, the calibrated \({S}_{v}\) values (Eq. 1) can be expressed as the sum of contributions from the signal and noise as:
where \({S}_{{v}_{{\rm{cal}}}}\) (dB re 1 m2 m−3) is the calibrated \({S}_{v}\) samples derived from the raw data (i.e. Eq. 1), \({S}_{{v}_{{\rm{signal}}}}\) (dB re 1 m2 m−3) is the calibrated \({S}_{v}\) samples representing the contribution from signal, \({S}_{{v}_{{\rm{noise}}}}\) (dB re 1 m2 m−3) is the calibrated \({S}_{v}\) samples representing the contribution from noise, and the index i and j represent vertical sample number and horizontal ping number respectively.
To estimate background noise levels, calibrated received power \({P}_{e{r}_{{\rm{cal}}}}[i,j]\) (dB re 1 W) values were calculated from \({S}_{{v}_{{\rm{cal}}}}[i,j]\) values by subtracting the time-varied gain (TVG) function2 (i.e. \(2{0\log }_{10}r+2{\alpha }_{a}r\)) from Eq. 1 as:
The calibrated \({P}_{e{r}_{{\rm{cal}}}}[i,j]\) values were averaged66 (in linear domain) within an ‘averaging cell’ of \(M\) vertical samples (with an index \(k\)) and \(N\) horizontal pings (with an index \(l\)) to estimate noise as:
where \(\bar{{P}_{e{r}_{{\rm{cal}}}}}[k,l]\) (dB re 1 W) is the averaged \({P}_{e{r}_{{\rm{cal}}}}[i,j]\) values calculated for each averaging cell with a vertical sample interval \(k\) and horizontal ping interval \(l\), and \(Noise\left(l\right)\) (dB re 1 W) is the representative noise estimate for the ‘middle ping’ in each horizontal interval \(l\). Note that the averaging cell slides over the entire echogram (see details of averaging cell in Table 6).
An empirically determined maximum threshold \(Nois{e}_{max}\) (dB re 1 W) (see Table 6) was applied to \(Noise\left(l\right)\) values as an upper limit of background noise levels. Any \(Noise\left(l\right)\) values exceeding this threshold was replaced with the predefined \(Nois{e}_{max}\) value.
The \(Noise\left(l\right)\) value estimated for a given horizontal ping interval \(l\) was assigned to all individual pings constituting the interval to establish noise \(Noise\left(j\right)\) (dB re 1 W) estimate for each ping. The effect of TVG was added to the \(Noise\left(j\right)\) levels to compute \({S}_{{v}_{{\rm{noise}}}}\) for each vertical sample number \(i\) and horizontal ping number \(j\) as:
The background noise corrected volume backscattering strength \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) (dB re 1 m2 m−3) values for each vertical sample number \(i\) and horizontal ping number \(j\) were estimated as:
The SNR, a measure of the relative contribution of signal and noise was estimated as:
where \(SNR[i,j]\) (dB re 1) is the signal-to-noise ratio for each vertical sample number \(i\) and horizontal ping number \(j\).
An empirically determined threshold \(Minimu{m}_{SNR}\) (dB re 1) (see Table 6) was used as an acceptable SNR for background noise corrected \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) data. The \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) values with corresponding \(SNR[i,j]\) below this threshold were set to ‘−999’ dB re 1 m2 m−3 (an approximation of zero in the linear domain). The background noise removal parameters defined in Echoview® are given in Table 6.
Residual noise removal
In the final stage, a 7 × 7 median filter was applied to remove residual noise retained in the core filtering stages (especially at far ranges). A median filter replaces the current \({S}_{v}\) sample with the median value of \({S}_{v}\) samples in a \(M\) × \(M\) neighbourhood. It is important to note that the output of 7 × 7 median filter was not directly used for echo-integration, rather it was used to flag residual noise retained from the core filtering process. A maximum data threshold of −50 dB re 1 m2 m−3 and a time-varied threshold \(TVT(r)\) with the reference value of −160 dB re 1 m2 m−3 (defined at 1 m range) was applied to the background noise corrected \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) data before applying 7 × 7 median filter (see Table 3 for a description of time-varied threshold). \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) values above the maximum threshold (i.e. −50 dB re 1 m2 m-3) were set to ‘−999’ dB re 1 m2 m−3. Similarly, \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) values below the calculated \(TVT(r)\) values were set to ‘−999’ dB re 1 m2 m-3 (note that median filter may replace ‘−999’ with the median of samples in the 7 × 7 neighbourhood). The output of the median filter was used to create a Boolean data range bitmap (between −998 to −20 dB re 1 m2 m−3) with ‘true’ or ‘false’ values for each sample. This Boolean data range bitmap was applied to the background noise corrected \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) data for removing any residual noise before echo-integration. \({S}_{{v}_{{\rm{bnc}}}}[i,j]\) values corresponding to ‘false’ values in the data range bitmap were set to ‘−999’ dB re 1 m2 m−3.
Quality-controlled \({S}_{v}\) data along with: (1) calibrated and motion corrected raw data, (2) transducer motion correction factor (i.e. difference between ‘motion corrected’ and ‘calibrated raw’ data), (3) background noise, and (4) SNR were exported from Echoview® as echo-integration cells (i.e. grid on an echogram) with a resolution of 1 km horizontal distance (i.e. ping-axis interval \(p\)) and 10 m vertical depth (i.e. range-axis interval \(r\)). Echo-integration values were stored as comma-separated values (CSV) files. Exported \({S}_{v}\) data were converted to linear scale for further processing and packaging in MATLAB® (Fig. 5).
Secondary corrections for sound speed and absorption variation
Quality-controlled \({S}_{v}\) data were echo-integrated and exported using a nominal sound speed \({c}_{w}\) (m s−1) and absorption coefficient \({\alpha }_{a}\) (dB m−1) values estimated using the equations of Mackenzie70 and Francois and Garrison71 respectively (see sound speed and absorption coefficient variables in Eq. 1 used for \({S}_{v}\) calculation). However, open ocean transects pass through different hydrographical conditions, so a secondary range dependent correction was required to account for the changes in horizontal and vertical cumulative mean sound speed and absorption as:
or in linear terms:
where \(\bar{{s}_{{v}_{{\rm{uncorr}}}}}[r,p]\) (m2 m−3) is the uncorrected (but filtered) volume backscattering coefficient values exported from Echoview® at the specified range-axis interval \(r\) (i.e. 10 m) and ping-axis interval \(p\) (i.e. 1 km), \({r}_{n}[r,p]\) (m) is the regularly spaced depth values for each echo-integration cell, \(\bar{{c}_{w}}\left[r,p\right]=\frac{{\sum }_{r=1}^{n}{c}_{w}\left[r,p\right]}{n};\,\forall p\) (m s−1) is the cumulative mean sound speed values estimated at each echo-integration cell for the new range \({r}_{a}[r,p]={r}_{n}[r,p]\frac{\bar{{c}_{w}}[r,p]}{{c}_{w}}\) (m) calculation, \(\bar{{\alpha }_{a}}\left[r,p\right]=10\,{{\rm{\log }}}_{10}\left(\frac{{\sum }_{r=1}^{n}1{0}^{\left(\frac{{\alpha }_{a}\left[r,p\right]}{10}\right)}}{n}\right);\forall p\) (dB m−1) is the cumulative mean absorption coefficient values ‘interpolated’ at the new range \({r}_{a}[r,p]\), and \(\bar{{s}_{{v}_{{\rm{corr}}}}}[r,p]\) (m2 m−3) is the corrected volume backscattering coefficient values at the new range \({r}_{a}[r,p]\).
Due to changes in cumulative mean sound speed, this correction step creates a grid with irregular \({r}_{a}[r,p]\) values. Therefore, the \(\bar{{s}_{{v}_{{\rm{corr}}}}}[r,p]\) values at the new ranges \({r}_{a}[r,p]\) were interpolated and reported at the regularly spaced \({r}_{n}[r,p]\) values.
The sound speed and absorption coefficient values for secondary corrections were estimated using the equations of Mackenzie70 and Francois and Garrison71 respectively. Francois and Garrison71 estimate their ‘total absorption equation’ to be accurate within 5% for ocean temperature values of −1.8–30 °C, frequencies of 0.4–1000 kHz, and salinity values of 30–35 PSU. The typical hydrographical conditions (temperature values of 0–27 °C and salinity values of 34–36 PSU) present along the open ocean transects are generally within the reliability limits of Francois and Garrison71 equation.
The temperature and salinity data for sound speed and absorption coefficient calculations were interpolated from either CSIRO Atlas of Regional Seas72 (CARS, http://www.marine.csiro.au/~dunn/cars2009/ version 2009) or Synthetic Temperature and Salinity (SynTS)73 analyses (http://www.marine.csiro.au/eez_data/doc/synTS.html), but can also be derived from oceanographic reanalysis and ocean circulation models. CARS2009 is a digital climatology or atlas of seasonal ocean water properties. It is based on a comprehensive set of quality‐controlled vertical profiles of in situ ocean properties (i.e. temperature, salinity, oxygen, nitrate, silicate, and phosphate) collected between 1950 and 2008. CARS2009 NetCDF files contain a gridded mean of these ocean properties and average seasonal cycles generated from the collated observations. CARS2009 covers global oceans on a 0.5 × 0.5 degree grid spatial resolution, and are mapped onto 79 standard depth levels from the sea surface to 5500 m (from this vertical profiles of ocean properties along a bioacoustic transect can be extracted). SynTS is a daily three-dimensional (3D) temperature and salinity product generated by CSIRO, where the CARS temperature and salinity fields are adjusted with daily satellite sea surface temperature (SST) and gridded sea level anomaly (GSLA). SynTS has a 0.2 × 0.2 degree grid spatial resolution, and is mapped onto 66 standard depth levels from the sea surface to 2000 m. Due to limited spatial coverage (60°S–10°N and 90°E–180°E), the SynTS products may not always cover the transect region (e.g. Southern Indian Ocean), in that case CARS climatology values were used for the secondary corrections (Fig. 5).
Data review, packaging and submission routines
For each processed transect, secondary corrections applied \(\bar{{s}_{{v}_{{\rm{corr}}}}}\) data together with metrics of data quality and other auxiliary data variables were stored in Network Common Data Form (NetCDF, www.unidata.ucar.edu) file (NetCDF-4 format) with a resolution of 1 km horizontal distance (i.e. ping-axis interval) and 10 m vertical depth (i.e. range-axis interval) (see ‘Data Records’ section for data contents). This NetCDF file conforms standardized naming conventions and metadata content defined by the Climate and Forecast (CF)74, IMOS75, and International Council for the Exploration of the Sea (ICES)76 published over the years (Fig. 6).
Primary components and organization of key variables present in a NetCDF file with illustrations of key metadata categories. A brief description of these key variables is given in Table 7.
Processed NetCDF files were independently reviewed by both analyst and principal investigator to further investigate data quality. If suitable, the NetCDF file along with ancillary files: (1) acquired raw data (.raw files), (2) platform track in CSV format (containing date, time, latitude, longitude, and time offset to UTC), (3) platform motion data (if recorded) in CSV format (including date, time, pitch, and roll measurements), and (4) a snapshot of processed echogram as Portable Network Graphics (PNG) format were packaged and submitted to the publicly accessible AODN Portal (Fig. 5).
Data Records
The primary components of a processed NetCDF file are shown in Fig. 6 and described in Table 7 to provide an overview of data contents and structure. Each variable in a NetCDF file is described with an associated description, specifying the data output resulting from each data-collection or analytical step (Table 7).
Processed NetCDF files are published via the Australian Ocean Data Network (AODN) Portal at:
https://portal.aodn.org.au/search?uuid=8edf509b-1481-48fd-b9c5-b95b42247f82.
This portal allows transect selection and data download with spatial and temporal subset options implemented for each platform and frequency.
A generic metadata record of the project is available via GeoNetwork at:
https://catalogue-imos.aodn.org.au/geonetwork/srv/api/records/8edf509b-1481-48fd-b9c5-b95b42247f82.
The NetCDF files are also accessible via the AODN THREDDS data server that can be accessed remotely using the OPeNDAP protocol at:
http://thredds.aodn.org.au/thredds/catalog/IMOS/SOOP/SOOP-BA/catalog.html.
A snapshot of processed NetCDF files at the time of this publication has been assigned a Digital Object Identifier (https://doi.org/10.26198/dv5p-t593) and will be maintained in perpetuity by the AODN77. Readers are directed to check the AODN Portal for the latest data set.
Technical Validation
Routine calibration and monitoring of echosounders
In the context of echosounder calibration, it is important to note that respective \(\pm X\) dB re 1 (where \(X\) is a real number) change in calibration parameters \({G}_{0}\) and \({S}_{a{\rm{c}}{\rm{o}}{\rm{r}}{\rm{r}}}\) factor represents a corresponding twofold \(\mp 2X\) dB re 1 m2 m-3 variation in the derived \({S}_{v}\) (Eq. 1) that would result in \(\mp \left(100\left(1{0}^{(2X/10)}\right)-100\right)\)% change echo-integration results (if accurate calibration parameters are not applied). In principle, properly calibrated echosounders operating at the same frequency should provide matching echo-integration results for a given sampling region. However, due to platform performance (e.g. aeration beneath the transducer), the derived data may be biased and this can be verified by an intercalibration4,78 experiment with two or more platforms simultaneously sailing over the same region, and later comparing the echo-integration results. In suitable circumstances, large uncertainty in the absolute calibrations and platform-specific factors can be quantified. This generic principle was applied to prioritize platforms for potential long-term data collection by comparing data quality metrics between participating platforms. As the spatio-temporal coverage of the data series improves, it will be possible to perform more direct comparisons between platforms and with an acoustic climatology of the regions.
Time series calibration results of selected platforms (with consistent echosounder configuration) are shown in Fig. 7 as an example to highlight repeatability and challenges with monitoring long-term performance and stability of echosounders. The FV Rehua, FV Antarctic Discovery, and RV Investigator demonstrate reasonable repeatability of 38 kHz transducer measurements with \({G}_{0}\) values varying between 25.4 ± 0.2, 27.0 ± 0.3, and 24.9 ± 0.2 dB re 1 respectively (Fig. 7a,c,d). In contrast, the FV Austral Leader II (Fig. 7b) indicates gradual degradation of system performance (possibly ageing effect) over six years with 1.3 dB re 1 decrease in calibrated \({G}_{0}\) values79. Keeping \({p}_{et}\), \(\tau \), \({\alpha }_{a}\), \({c}_{w}\), and \(\psi \) constant (Eq. 1), this performance change would result in ~44% decrease in \({S}_{v}\) data if \({G}_{0}\) and \({S}_{a{\rm{c}}{\rm{o}}{\rm{r}}{\rm{r}}}\) factor calculated in 2009 is applied for processing 2015 data sets.
Monitoring long-term performance and stability of echosounders. Panels (a–d) show 38 kHz calibrated G0 (blue solid line) and \({S}_{a{\rm{c}}{\rm{o}}{\rm{r}}{\rm{r}}}\) factor (red dash line) for (a) FV Rehua (ES38-B SN30218), (b) FV Austral Leader II (ES38-B SN30835), (c) FV Antarctic Discovery (ES38-7 SN111), and (d) RV Investigator (ES38-B SN31167) with consistent echosounder configuration. (e) Spatial and temporal variations in peak power \({P}_{er}\) (measured within 0–1 m range) for FV Atlas Cove (ES38-7 SN171) over a year. (f) A comparison between 18 (ES-18 SN2112) and 38 kHz (ES38-7 SN111) peak power values for FV Antarctic Discovery covering 15 days docking period, highlighting the importance of routine monitoring and calibration.
Although the established sphere calibration method standardizes bioacoustic data collected by multiple participating platforms, there is a need for an additional diagnostic method to ensure echosounder performance in between routine calibrations. Along with calibration results, the peak values of instantaneous received power \({P}_{er}\) (Eq. 1) measured within 0–1 m range (i.e. ringdown zone) are used as a complementary diagnostic method to ensure stability of echosounders, noting that monitoring is not calibration. This method can highlight noticeable gradual or abrupt changes in system performance over time. For example, spatio-temporal variations in peak power for FV Atlas Cove (Fig. 7e) highlight gradual degradation of 38 kHz echosounder performance with ~11 dB re 1 W decrease in peak power values over a year, complicating data usage. In contrast, a comparison between 18 and 38 kHz peak power values for FV Antarctic Discovery (Fig. 7f) highlights an unknown abrupt change (~3 dB re 1 W) in 18 kHz echosounder performance over 15 days docking period, necessitating routine monitoring. Such performance changes (if observed) are reported back to the operator for system maintenance (Fig. 1), and juxtaposed with relevant calibration results to assess repeatability of measurements and prioritizing transects for processing.
Simmonds and MacLennan2 consider that in fisheries acoustics applications, properly maintained low-frequency scientific echosounders can demonstrate consistent performance within 10% in the long-term. The aim should be to develop a routine or protocol for calibration that would help achieve this accuracy consistently irrespective of the echosounder system used. But in practice, variability in echosounder on-axis sensitivity could result from a combination of factors including system electronics, data acquisition settings, SNR, environmental conditions, and density and composition of the calibration sphere3. The performance of an echosounder may degrade gradually or abruptly (Fig. 7e,f), and transducers are vulnerable to mechanical damage and ageing effects80. Therefore, it is important to quantify such changes routinely for all participating platforms to apply suitable calibration corrections required for data processing. This would further facilitate existing feedback mechanism with platform operators for subsequent system maintenance and technical inspection.
Transducer motion correction
Transducer motion can reduce the received signal and degrade data quality substantially at long ranges depending on the sea state and platform design. For hull-mounted circular transducer, the platform motion and transducer motion can be considered synonymous81. Accordingly, the angular motion of platform can be used to correct for the change in orientation of transducer beam between the times of each ping, with a precondition that platform motion data (i.e. pitch and roll) need to be recorded at a sampling rate above the Nyquist rate of platform’s angular motion. The Power Spectral Density (PSD) analyses82 of motion data (Fig. 8a) recorded from selected platforms indicate that a minimum sampling rate of 4 Hz is generally adequate to meet this precondition and subsequent correction. Sources of error may exist in motion-corrected data if there is a large discrepancy between measured and manufacturer specified (or nominal) beamwidths of the transducer used83.
Importance of transducer motion correction. (a) Checking the precondition of Dunford68 algorithm using PSD analyses of motion data recorded by selected vessels with varying dimensions and range of weather conditions, indicating the strength of variations (energy) in pitch and roll data as a function of waveform frequency. Recorded pitch and roll data were converted from Cartesian to polar coordinate for translating platform motion as transducer angle off-axis. (b) Shows spectrogram analysis of example motion data recorded by RV Investigator at a sampling rate of 10 Hz, indicating temporal variations in waveform frequencies with insignificant energy contribution from rapid vessel movements above 2 Hz. Panels (c,d) display magnitudes and effects of transducer motion correction (see Table 7 for description) applied to 18 and 38 kHz calibrated raw \({s}_{v}\) data recorded onboard RV Investigator during 12–13 March 2018 in Southern Ocean, highlighting expected changes between beamwidths of transducers used. Similarly, (e) the magnitudes of motion correction applied to 38 kHz calibrated raw \({s}_{v}\) data recorded onboard FV Isla Eden during 06–16 June 2019 in Southern Indian Ocean is provided to highlight appreciable changes between vessel design and nature of sea state. Note the non-linear range dependent effect in all cases. In boxplots, the vertical line inside of each box is the sample median. The right and left edges of each box are the upper and lower quartiles respectively. The distance between the right and left edges is the interquartile range (IQR). Values that are more than 1.5 IQR away from the right or left of the box are outliers (red plus sign).
Owing to the magnitude of angular displacement and beamwidth values of transducers used, the effects of transducer motion can result in a non-linear range dependent \({s}_{v}\) correction. If motion correction is not applied, it can negatively bias (or underestimate) echo-integration results, where the amount of correction increases with range. The correction is greater for narrow-beam transducers and comparatively smaller for wide-beam transducers (Fig. 8c,d). The variable ‘motion_correction_factor’ (Table 7) is now being stored in NetCDF files for assessing the magnitude of transducer motion correction and recalculating calibrated raw data (if needed).
Associated global attributes (Fig. 6) ‘data_processing_motion_correction’ and ‘data_processing_motion_correction_description’ capture important metadata of transducer motion correction applied.
Data processing filters
The quality of bioacoustic data collected from ships of opportunity sampling methods can be complex and extremely variable. If noise is not removed, it can be misinterpreted as biological signal, biasing echo-integration results. Statistical quantification of bias and error potential for data retained after filtering is challenging and beyond the scope of present study. However, selected examples of bioacoustic data with good and compromised quality are presented to demonstrate combined effectiveness of data processing filters. The application of data processing filters has considerably improved the quality of bioacoustic data and demonstrated to be robust across diverse platforms and weather conditions5. A caution is that there are subjective elements in ‘visually’ determining the quality of final data product after filtering, but this can be made objective to a certain extent by comparing raw and filtered echograms with metrics of data quality stored in NetCDF files.
As an example, good quality data collected by FV Will Watch in the Indian Ocean is presented in Fig. 9, highlighting diel vertical migration and deep scattering layer without any apparent artefacts in the data. To broadly quantify the combined effect of data processing filters, mean difference between unfiltered and filtered echograms (i.e. difference in mean \({S}_{v}\) before and after filtering) is calculated for epipelagic, upper mesopelagic, and lower mesopelagic layers respectively, indicating 0.3 ± 0.9 (~7%), 0.1 ± 0.4 (~2%), and 0.1 ± 0.1 dB re 1 m2 m-3 (~2%) reduction in the filtered data (see Table 7 for layer description). The data quality metric SNR (Fig. 9b) in epipelagic, upper mesopelagic, and lower mesopelagic layers are 59.1 ± 4.6, 34.6 ± 3.5, and 31.5 ± 4.4 dB re 1 respectively, with mean ping-axis interval background noise level calculated as −165.6 ± 2.1 dB re 1 W (Fig. 9c). After the filtering process, approximately 98%, 98%, and 99% of \({S}_{v}\) data are retained in the epipelagic, upper mesopelagic, and lower mesopelagic layers respectively (Fig. 9d).
Example of good quality data comparing unfiltered and filtered echograms with metrics of data quality. The 38 kHz data was collected by FV Will Watch transiting from Mauritius to South-West Indian Ocean. (a) Displays calibrated and motion correction applied echogram before the application data processing filters outlined in Fig. 5. Panels (b,c) show SNR and background noise level calculated after background noise removal filter used in the filtering stage. (d) Depicts percentage of data retained after the filtering process. (e) Filtered data before applying secondary corrections for sound speed and absorption variation.
To demonstrate the usefulness of data quality metrics, data collected by FV San Tongariro in Tasman Sea is presented in Fig. 10. This example compares raw and filtered echograms, highlighting predominant transient noise in the data amplified as a function of TVG. The mean difference between unfiltered and filtered echograms in epipelagic, upper mesopelagic, and lower mesopelagic layers respectively indicates 1.7 ± 1.9 (~48%), 1.2 ± 1.5 (~31%), and 3.6 ± 1.8 dB re 1 m2 m-3 (~129%) reduction in the filtered data, highlighting range-dependant effect of combined noise5 (i.e. the sum of impulse, transient, and background noise). Associated data quality metric SNR (Fig. 10b) in epipelagic, upper mesopelagic, and lower mesopelagic layers are 32.6 ± 7.9, 22.2 ± 5.3, and 17.8 ± 4.4 dB re 1 respectively, with mean ping-axis interval background noise level (Fig. 10c) calculated as −152.5 ± 3.4 dB re 1 W (note this background noise is ~13 dB re 1 W higher as compared to the good quality data presented in Fig. 9c). After the filtering process, approximately 84%, 88%, and 86% of \({S}_{v}\) data are retained in the epipelagic, upper mesopelagic, and lower mesopelagic layers respectively (Fig. 10d). The raw data quality of this transect is not satisfactory (Fig. 10a) and despite the visual appearance of filtered data, the quality metrics SNR, background noise, and percentage of \({S}_{v}\) data retained after filtering are not considered to be acceptable as compared to the other transect with high data quality (Fig. 9a).
Example of compromised quality data comparing unfiltered and filtered echograms with metrics of data quality. The 38 kHz data was collected by a prospective FV San Tongariro transiting from Hobart to New Zealand in Tasman Sea. (a) Displays calibrated and motion correction applied echogram before the application data processing filters outlined in Fig. 5. Panels (b,c) show SNR and background noise level calculated after background noise removal filter used in the filtering stage. (d) Depicts percentage of data retained after the filtering process. (e) Filtered data before applying secondary corrections for sound speed and absorption variation.
Similarly, data acquired by FV Isla Eden is presented in Fig. 11, highlighting an abrupt (~5 dB re 1 W) change in the background noise level over 24 hours, presumably indicating electrical interference and electrical noise in the echosounder. The mean difference between unfiltered and filtered echograms in epipelagic, upper mesopelagic, and lower mesopelagic layers respectively indicates 1.0 ± 2.1 (~25%), 1.0 ± 1.6 (~25%), and 1.4 ± 1.2 dB re 1 m2 m-3 (~38%) reduction in the filtered data, predominantly highlighting range-dependant effect of background noise. Related data quality metric SNR (Fig. 11b) in epipelagic, upper mesopelagic, and lower mesopelagic layers are 37.5 ± 8.2, 12.9 ± 4.2, and 12.9 ± 2.3 dB re 1 respectively, with mean ping-axis interval background noise level (Fig. 11c) calculated as −145.5 ± 2.1 dB re 1 W (note this background noise is ~20 dB re 1 W higher as compared to the good quality data presented in Fig. 9c). After the filtering process, approximately 89%, 85%, and 82% of \({S}_{v}\) data are retained in the epipelagic, upper mesopelagic, and lower mesopelagic layers respectively (Fig. 11d).
Another example of compromised quality data comparing unfiltered and filtered echograms with metrics of data quality. The 38 kHz data was collected by FV Isla Eden transiting from Mauritius to Heard Island and McDonald Islands in Southern Indian Ocean. (a) Displays calibrated and motion correction applied echogram before the application data processing filters outlined in Fig. 5. Panels (b,c) show SNR and ‘smoothed’ background noise level calculated after background noise removal filter used in the filtering stage. Note that the triangle wave error present in background noise level was smoothed for comparison purposes. For this transect, the error was not averaged to zero over the 1 km horizontal distance, possibly due to slow ping rate achieved. (d) Depicts percentage of data retained after the filtering process. (e) Filtered data before applying secondary corrections for sound speed and absorption variation.
These examples (Figs. 10 and 11) suggest that caution is needed while reviewing a final data product where filtering and subsequent resampling to predefined NetCDF file resolution (1 km horizontal distance and 10 m vertical depth) may produce a visually clean echogram without any apparent artefacts, but potentially removed significant biological signal and/or retained noise in the process. Accordingly, we have not posted these two transects to the AODN, and similar data sets from other platforms with compromised data quality are archived locally. Storing metrics of data quality in NetCDF files is intended for assisting users to make an independent assessment of data quality based on the examples demonstrated here.
Secondary corrections for sound speed and absorption variation
The difference between variable ‘uncorrected_Sv’ (i.e. filtered data before secondary corrections) and ‘abs_corrected_sv’ (i.e. same data after secondary corrections but before depth interpolation) is calculated (uncorrected_Sv—abs_corrected_sv) to demonstrate the effect of secondary corrections (Fig. 12). This step introduces a range-dependent correction (Fig. 12f) that can differ substantially based on the equation used for calculating sound absorption in seawater (see Fig. 5 in Doonan, et al.84 for a comparison between two commonly used equations for absorption calculation. Note that the range-dependant percentage correction to the data can differ up to 45% between Doonan, et al.84 and Francois and Garrison71 for a 38 kHz data at 1000 m depth).
Secondary corrections for sound speed and absorption variation. The transect presented in Fig. 9 is used to highlight the nature of corrections. (a) Filtered but uncorrected echogram before applying secondary corrections. (b) Shows filtered and corrected echogram after applying secondary corrections with (c) result correction matrix. Bottom panels show the (d) cumulative mean sound speed and (e) absorption coefficient values used for the correction (Eq. 12), highlighting the nature of (f) range-dependant percentage correction applied to the final data product before depth interpolation. The nominal sound speed and absorption coefficient values used for the correction are highlighted as vertical green lines. In boxplots, the vertical line inside of each box is the sample median. The right and left edges of each box are the upper and lower quartiles respectively. The distance between the right and left edges is the interquartile range (IQR). Values that are more than 1.5 IQR away from the right or left of the box are outliers (red plus sign).
The processed bioacoustic data sets are consistently corrected based on Mackenzie70 sound speed and Francois and Garrison71 absorption equations following the recommendations by Simmonds and MacLennan2 until more evidence is available to select another formula. Macaulay, et al.85 conducted field measurements of acoustic absorption in seawater from 38 to 360 kHz, indicating consistent results with Francois and Garrison71 equation for frequencies of 200 kHz and lower. Macaulay, et al.85 observed a significant difference around 333 kHz, indicating that Francois and Garrison71 equation is incorrect for some input parameters (note that 333 kHz data is not processed under IMOS Bioacoustics sub-Facility).
It is important to note that the percentage correction shown in Fig. 12 is applicable to the example transect only that depends on the nominal sound speed and absorption values used during initial processing and echo-integration (Eq. 1). Other transects (e.g. Southern Ocean) have different correction factors that are related to regional changes in temperature and salinity values.
The key intermediate variable ‘uncorrected_Sv’ is stored in NetCDF files for recalculating secondary corrections using other equations or data sources (if needed). The equation used for sound absorption calculation is documented in the global attribute section of a NetCDF file as ‘data_processing_absorption_description’ and ‘history’. Similarly, the equation used for sound speed calculation is captured in the global attributes ‘data_processing_soundspeed_description’ and ‘history’.
Usage Notes
When interpreting bioacoustic data it is important to understand the corrections applied at each processing step particularly calibration, transducer motion correction, data filtering, and secondary corrections for sound speed and absorption variation (Fig. 5). The transducer motion and secondary corrections are range-dependant that can greatly influence the lower mesopelagic layer derived metrics. Our goal is to keep minimum updates to data processing steps and data records so that the database remains consistent and comparable.
Measurement uncertainty
The widely used Simrad EK60 echosounder is now discontinued and replaced by the Simrad EK80. A recent comparison study86 highlighted that EK80 raw power measurements were 3–12% lower as compared to EK60, affecting weak scatterer and/or long-range acoustic observations due to nonlinear amplification of low-power signals by the EK60. Presently the users need to correct the data for this bias, and we are in the process of providing a correction update to the data sets with associated metadata. In addition to calibration and unknown methodological uncertainties, this new measurement uncertainty highlights the ongoing challenges in maintaining a diverse data series, and the need for storing fundamental echosounder measurement (i.e. received echo power) and appropriate metadata to enable unforeseen corrections in the future as needed.
Challenges with biomass estimation
Ships of opportunity bioacoustic sampling methods have clear advantages as well as limitations. Their usefulness in resource assessment, ecosystem monitoring, and cost-effective mapping of mesopelagic communities at regional and global scales is established with diverse acoustic-based indicators and metrics, but credible conversion of bioacoustic data (\({s}_{v}\)) to open ocean fish biomass is a multi-step procedure and require lowest degree of bias.
For example, the processed \({s}_{v}\) values are vertically integrated over a measurement range (\({r}_{1}\) to \({r}_{2}\)) to calculate area backscattering coefficient \({s}_{a}\) (m2 m−2) along a transect. Scatterer areal density (number m−2) i.e. the number of organisms (e.g. fish) within the measurement range is calculated by dividing \({s}_{a}\) by the backscattering cross-section \({\sigma }_{bs}\) (m2) of a representative single fish. Biomass of fish (kg m−2) can be estimated by multiplying this scatterer areal density by the weight \(W\) (kg) of a single fish. This requires separation of bioacoustic data by species composition, location, and \({\sigma }_{bs}\) distribution. Mean weight can be derived from observed weights (using nets) or length to weight regression. Similarly, \({\sigma }_{bs}\) are obtained from in situ measurements and/or \({\sigma }_{bs}\)to length regressions2. Biomass calculations from these equations will be biased if the weight and target strength \(TS\) [\(10\,{{\rm{\log }}}_{10}({\sigma }_{bs})\), dB re 1 m2] of the organism are uncertain (assuming accurate calibration and echosounder linearity). For that reason, in situ and/or modelled \(TS\) must be calculated with the goal of obtaining a representative distribution.
Credible estimation of biomass using a vessel-based echosounder is very difficult for the highly diverse mesopelagic community, where gas inclusions may present in many organisms (depending on the region) that can cause frequency- and depth-dependent resonance scattering87, dominating the received signal. Multiple methods of ecosystem models, net capture, acoustic backscattering models, and in situ profiling acoustic optical systems19,88 are needed to provide the necessary information to convert basin-scale bioacoustic data into specific biological metrics such as species-specific biomass61.
Reading the data
Generated data are stored in NetCDF files that can be readily imported into a wide variety of cross-platform software programs and programming languages. A custom MATLAB® function ‘viz_sv’ to read and visualize NetCDF files conforming to the conventions described in this data descriptor can be downloaded from the IMOS Bioacoustics sub-Facility web site http://imos.org.au/facilities/shipsofopportunity/bioacoustic or GitHub https://github.com/CSIRO-Acoustics/Visualize-IMOS-Bioacoustics-data.
Terms of use
All NetCDF files are released under the license Creative Commons Attribution 4.0 International (CC-BY 4.0, https://creativecommons.org/licenses/by/4.0/). Any users of IMOS data are required to clearly acknowledge the source of the material in the format: “Data was sourced from Australia’s Integrated Marine Observing System (IMOS) – IMOS is enabled by the National Collaborative Research Infrastructure Strategy (NCRIS). It is operated by a consortium of institutions as an unincorporated joint venture, with the University of Tasmania as Lead Agent.”
Code availability
Echosounder raw data files are recorded in proprietary formats that typically require dedicated commercial or open-source acoustic processing software for visualization and processing. The custom Java software tool ‘basoop.jar’ used for incoming data registration and management, along with the MATLAB® GUI used for controlling data processing steps in Echoview® and NetCDF file creation can be obtained at: https://github.com/CSIRO-Acoustics/IMOS-Bioacoustics. The MATLAB® codes used for generating relevant figures are available at: https://github.com/CSIRO-Acoustics/Publications/tree/main/Scientific_Data/Data_Descriptor.
References
Kloser, R. J., Ryan, T. E., Young, J. W. & Lewis, M. E. Acoustic observations of micronekton fish on the scale of an ocean basin: potential and challenges. ICES J. Mar. Sci. 66, 998–1006, https://doi.org/10.1093/icesjms/fsp077 (2009).
Simmonds, J. & MacLennan, D. N. Fisheries Acoustics: Theory and Practice. 2 edn, (Blackwell Science, 2005).
Demer, D. et al. Calibration of acoustic instruments. ICES Coop. Res. Rep. 326, 1–133, https://doi.org/10.17895/ices.pub.5494 (2015).
Foote, K. G., Knudsen, H. P., Vestnes, G., MacLennan, D. N. & Simmonds, E. Calibration of acoustic instruments for fish density estimation: a practical guide. ICES Coop. Res. Rep. 144, 1–69 (1987).
Ryan, T. E., Downie, R. A., Kloser, R. J. & Keith, G. Reducing bias due to noise and attenuation in open-ocean echo integration data. ICES J. Mar. Sci. 72, 2482–2493, https://doi.org/10.1093/icesjms/fsv121 (2015).
Irigoien, X. et al. Large mesopelagic fishes biomass and trophic efficiency in the open ocean. Nat. Commun. 5, 3271, https://doi.org/10.1038/ncomms4271 (2014).
Proud, R., Handegard, N. O., Kloser, R. J., Cox, M. J. & Brierley, A. S. From siphonophores to deep scattering layers: uncertainty ranges for the estimation of global mesopelagic fish biomass. ICES J. Mar. Sci. 76, 718–733, https://doi.org/10.1093/icesjms/fsy037 (2018).
Bianchi, D. & Mislan, K. A. S. Global patterns of diel vertical migration times and velocities from acoustic data. Limnol. Oceanogr. 61, 353–364, https://doi.org/10.1002/lno.10219 (2016).
Brierley, A. S. Diel vertical migration. Curr. Biol. 24, R1074–R1076, https://doi.org/10.1016/j.cub.2014.08.054 (2014).
Klevjer, T. A. et al. Large scale patterns in vertical distribution and behaviour of mesopelagic scattering layers. Sci. Rep. 6, 19873, https://doi.org/10.1038/srep19873 (2016).
St. John, M. A. et al. A Dark Hole in Our Understanding of Marine Ecosystems and Their Services: Perspectives from the Mesopelagic Community. Front. Mar. Sci. 3, https://doi.org/10.3389/fmars.2016.00031 (2016).
Anderson, T. R. et al. Quantifying carbon fluxes from primary production to mesopelagic fish using a simple food web model. ICES J. Mar. Sci. 76, 690–701, https://doi.org/10.1093/icesjms/fsx234 (2018).
Aumont, O., Maury, O., Lefort, S. & Bopp, L. Evaluating the Potential Impacts of the Diurnal Vertical Migration by Marine Organisms on Marine Biogeochemistry. Glob. Biogeochem. Cycles 32, 1622–1643, https://doi.org/10.1029/2018gb005886 (2018).
Cavan, E. L., Laurenceau-Cornec, E. C., Bressac, M. & Boyd, P. W. Exploring the ecology of the mesopelagic biological pump. Prog. Oceanogr. 176, 102125, https://doi.org/10.1016/j.pocean.2019.102125 (2019).
Davison, P., Checkley Jr, D., Koslow, J. & Barlow, J. Carbon export mediated by mesopelagic fishes in the northeast Pacific Ocean. Prog. Oceanogr. 116, 14–30, https://doi.org/10.1016/j.pocean.2013.05.013 (2013).
Kelly, T. B. et al. The Importance of Mesozooplankton Diel Vertical Migration for Sustaining a Mesopelagic Food Web. Front. Mar. Sci. 6, https://doi.org/10.3389/fmars.2019.00508 (2019).
Davison, P. C., Koslow, J. A. & Kloser, R. J. Acoustic biomass estimation of mesopelagic fish: backscattering from individuals, populations, and communities. ICES J. Mar. Sci. 72, 1413–1424, https://doi.org/10.1093/icesjms/fsv023 (2015).
Godø, O. R., Patel, R. & Pedersen, G. Diel migration and swimbladder resonance of small fish: some implications for analyses of multifrequency echo data. ICES J. Mar. Sci. 66, 1143–1148, https://doi.org/10.1093/icesjms/fsp098 (2009).
Kloser, R. J., Ryan, T. E., Keith, G. & Gershwin, L. Deep-scattering layer, gas-bladder density, and size estimates using a two-frequency acoustic and optical probe. ICES J. Mar. Sci. 73, 2037–2048, https://doi.org/10.1093/icesjms/fsv257 (2016).
Korneliussen, R. J., Diner, N., Ona, E., Berger, L. & Fernandes, P. G. Proposals for the collection of multifrequency acoustic data. ICES J. Mar. Sci. 65, 982–994, https://doi.org/10.1093/icesjms/fsn052 (2008).
Korneliussen, R. J. & Ona, E. An operational system for processing and visualizing multi-frequency acoustic data. ICES J. Mar. Sci. 59, 293–313, https://doi.org/10.1006/jmsc.2001.1168 (2002).
Anderson, C., Horne, J. & Boyle, J. Classifying multi-frequency fisheries acoustic data using a robust probabilistic classification technique. J. Acoust. Soc. Am. 121, EL230–EL237, https://doi.org/10.1121/1.2731016 (2007).
Béhagle, N. et al. Acoustic distribution of discriminated micronektonic organisms from a bi-frequency processing: The case study of eastern Kerguelen oceanic waters. Prog. Oceanogr. 156, 276–289, https://doi.org/10.1016/j.pocean.2017.06.004 (2017).
De Robertis, A., McKelvey, D. R. & Ressler, P. H. Development and application of an empirical multifrequency method for backscatter classification. Can. J. Fish. Aquat. Sci. 67, 1459–1474, https://doi.org/10.1139/F10-075 (2010).
Fielding, S., Watkins, J. L., Collins, M. A., Enderlein, P. & Venables, H. J. Acoustic determination of the distribution of fish and krill across the Scotia Sea in spring 2006, summer 2008 and autumn 2009. Deep Sea Res. Part II 59, 173–188, https://doi.org/10.1016/j.dsr2.2011.08.002 (2012).
Jech, J. M. & Michaels, W. L. A multifrequency method to classify and evaluate fisheries acoustics data. Can. J. Fish. Aquat. Sci. 63, 2225–2235, https://doi.org/10.1139/f06-126 (2006).
Kloser, R. J., Ryan, T., Sakov, P., Williams, A. & Koslow, J. A. Species identification in deep water using multiple acoustic frequencies. Can. J. Fish. Aquat. Sci. 59, 1065–1077, https://doi.org/10.1139/f02-076 (2002).
Korneliussen, R. J. & Ona, E. Synthetic echograms generated from the relative frequency response. ICES J. Mar. Sci. 60, 636–640, https://doi.org/10.1016/s1054-3139(03)00035-3 (2003).
Peña, M. Robust clustering methodology for multi-frequency acoustic data: A review of standardization, initialization and cluster geometry. Fish. Res. 200, 49–60, https://doi.org/10.1016/j.fishres.2017.12.013 (2018).
Demer, D. et al. 2016 USA–Norway EK80 Workshop Report: Evaluation of a wideband echosounder for fisheries and marine ecosystem science. ICES Coop. Res. Rep. 336, 1–70, https://doi.org/10.17895/ices.pub.2318 (2017).
Ladroit, Y., Escobar-Flores, P. C., Schimel, A. C. G. & O’Driscoll, R. L. ESP3: An open-source software for the quantitative processing of hydro-acoustic data. SoftwareX 12, 100581, https://doi.org/10.1016/j.softx.2020.100581 (2020).
Perrot, Y. et al. Matecho: An Open-Source Tool for Processing Fisheries Acoustics Data. Acoust. Aust. 46, 241–248, https://doi.org/10.1007/s40857-018-0135-x (2018).
Wall, C. C., Jech, J. M. & McLean, S. J. Increasing the accessibility of acoustic data through global access and imagery. ICES J. Mar. Sci. 73, 2093–2103, https://doi.org/10.1093/icesjms/fsw014 (2016).
Benoit-Bird, K. J. & Lawson, G. L. Ecological Insights from Pelagic Habitats Acquired Using Active Acoustic Techniques. Annu. Rev. Mar. Sci. 8, 463–490, https://doi.org/10.1146/annurev-marine-122414-034001 (2016).
Koslow, J. A. The role of acoustics in ecosystem-based fishery management. ICES J. Mar. Sci. 66, 966–973, https://doi.org/10.1093/icesjms/fsp082 (2009).
Godø, O. R. et al. Marine ecosystem acoustics (MEA): quantifying processes in the sea at the spatio-temporal scales on which they occur. ICES J. Mar. Sci. 71, 2357–2369, https://doi.org/10.1093/icesjms/fsu116 (2014).
Trenkel, V. M., Handegard, N. O. & Weber, T. C. Observing the ocean interior in support of integrated management. ICES J. Mar. Sci. 73, 1947–1954, https://doi.org/10.1093/icesjms/fsw132 (2016).
Trenkel, V. M., Ressler, P. H., Jech, M., Giannoulaki, M. & Taylor, C. Underwater acoustics for ecosystem-based management: state of the science and proposals for ecosystem indicators. Mar. Ecol. Prog. Ser. 442, 285–301, https://doi.org/10.3354/meps09425 (2011).
Béhagle, N. et al. Acoustic micronektonic distribution is structured by macroscale oceanographic processes across 20–50°S latitudes in the South-Western Indian Ocean. Deep Sea Res. Part I 110, 20–32, https://doi.org/10.1016/j.dsr.2015.12.007 (2016).
Boswell, K. M. et al. Oceanographic Structure and Light Levels Drive Patterns of Sound Scattering Layers in a Low-Latitude Oceanic System. Front. Mar. Sci. 7, https://doi.org/10.3389/fmars.2020.00051 (2020).
Della Penna, A. & Gaube, P. Mesoscale Eddies Structure Mesopelagic Communities. Front. Mar. Sci. 7, https://doi.org/10.3389/fmars.2020.00454 (2020).
Embling, C. B., Sharples, J., Armstrong, E., Palmer, M. R. & Scott, B. E. Fish behaviour in response to tidal variability and internal waves over a shelf sea bank. Prog. Oceanogr. 117, 106–117, https://doi.org/10.1016/j.pocean.2013.06.013 (2013).
Fennell, S. & Rose, G. Oceanographic influences on Deep Scattering Layers across the North Atlantic. Deep Sea Res. Part I 105, 132–141, https://doi.org/10.1016/j.dsr.2015.09.002 (2015).
Godø, O. R. et al. Mesoscale Eddies Are Oases for Higher Trophic Marine Life. PLOS ONE 7, e30161, https://doi.org/10.1371/journal.pone.0030161 (2012).
Kaartvedt, S., Klevjer, T. A. & Aksnes, D. L. Internal wave-mediated shading causes frequent vertical migrations in fishes. Mar. Ecol. Prog. Ser. 452, 1–10, https://doi.org/10.3354/meps09688 (2012).
Lavery, A. C., Chu, D. & Moum, J. N. Observations of Broadband Acoustic Backscattering From Nonlinear Internal Waves: Assessing the Contribution From Microstructure. IEEE J. Ocean. Eng. 35, 695–709, https://doi.org/10.1109/JOE.2010.2047814 (2010).
Sato, M. et al. Coastal upwelling fronts as a boundary for planktivorous fish distributions. Mar. Ecol. Prog. Ser. 595, 171–186, https://doi.org/10.3354/meps12553 (2018).
Stranne, C. et al. Acoustic Mapping of Thermohaline Staircases in the Arctic Ocean. Sci. Rep. 7, 15192, https://doi.org/10.1038/s41598-017-15486-3 (2017).
Cade, D. E. & Benoit-Bird, K. J. Depths, migration rates and environmental associations of acoustic scattering layers in the Gulf of California. Deep Sea Res. Part I 102, 78–89, https://doi.org/10.1016/j.dsr.2015.05.001 (2015).
Lawson, G. L., Wiebe, P. H., Ashjian, C. J. & Stanton, T. K. Euphausiid distribution along the Western Antarctic Peninsula—Part B: Distribution of euphausiid aggregations and biomass, and associations with environmental features. Deep Sea Res. Part II 55, 432–454, https://doi.org/10.1016/j.dsr2.2007.11.014 (2008).
Receveur, A. et al. Seasonal and spatial variability in the vertical distribution of pelagic forage fauna in the Southwest Pacific. Deep Sea Res. Part II 175, 104655, https://doi.org/10.1016/j.dsr2.2019.104655 (2020).
Aksnes, D. L. et al. Light penetration structures the deep acoustic scattering layers in the global ocean. Sci. Adv. 3, e1602468, https://doi.org/10.1126/sciadv.1602468 (2017).
Benoit-Bird, K. J., Au, W. W. L. & Wisdoma, D. W. Nocturnal light and lunar cycle effects on diel migration of micronekton. Limnol. Oceanogr. 54, 1789–1800, https://doi.org/10.4319/lo.2009.54.5.1789 (2009).
Last, K. S., Hobbs, L., Berge, J., Brierley, A. S. & Cottier, F. Moonlight Drives Ocean-Scale Mass Vertical Migration of Zooplankton during the Arctic Winter. Curr. Biol. 26, 244–251, https://doi.org/10.1016/j.cub.2015.11.038 (2016).
Bertrand, A., Ballón, M. & Chaigneau, A. Acoustic Observation of Living Organisms Reveals the Upper Limit of the Oxygen Minimum Zone. PLOS ONE 5, e10330, https://doi.org/10.1371/journal.pone.0010330 (2010).
Bianchi, D., Galbraith, E. D., Carozza, D. A., Mislan, K. A. S. & Stock, C. A. Intensification of open-ocean oxygen depletion by vertically migrating animals. Nat. Geosci. 6, 545–548, https://doi.org/10.1038/ngeo1837 (2013).
Netburn, A. N. & Koslow, A. J. Dissolved oxygen as a constraint on daytime deep scattering layer depth in the southern California current ecosystem. Deep Sea Res. Part I 104, 149–158, https://doi.org/10.1016/j.dsr.2015.06.006 (2015).
Boersch-Supan, P. H., Rogers, A. D. & Brierley, A. S. The distribution of pelagic sound scattering layers across the southwest Indian Ocean. Deep Sea Res. Part II 136, 108–121, https://doi.org/10.1016/j.dsr2.2015.06.023 (2017).
Proud, R., Cox, M. J. & Brierley, A. S. Biogeography of the Global Ocean’s Mesopelagic Zone. Curr. Biol. 27, 113–119, https://doi.org/10.1016/j.cub.2016.11.003 (2017).
Escobar-Flores, P., O’Driscoll, R. L. & Montgomery, J. C. Acoustic characterization of pelagic fish distribution across the South Pacific Ocean. Mar. Ecol. Prog. Ser. 490, 169–183, https://doi.org/10.3354/meps10435 (2013).
Handegard, N. O. et al. Towards an acoustic‐based coupled observation and modelling system for monitoring and predicting ecosystem dynamics of the open ocean. Fish Fish. 14, 605–615, https://doi.org/10.1111/j.1467-2979.2012.00480.x (2013).
Lehodey, P. et al. Optimization of a micronekton model with acoustic data. ICES J. Mar. Sci. 72, 1399–1412, https://doi.org/10.1093/icesjms/fsu233 (2014).
Constable, A. J. et al. Developing priority variables (“ecosystem Essential Ocean Variables” — eEOVs) for observing dynamics and change in Southern Ocean ecosystems. J. Mar. Syst. 161, 26–41, https://doi.org/10.1016/j.jmarsys.2016.05.003 (2016).
Maclennan, D. N., Fernandes, P. G. & Dalen, J. A consistent approach to definitions and symbols in fisheries acoustics. ICES J. Mar. Sci. 59, 365–369, https://doi.org/10.1006/jmsc.2001.1158 (2002).
Ryan, T. & Kloser, R. QUANTIFICATION AND CORRECTION OF A SYSTEMATIC ERROR IN SIMRAD ES60 ECHOSOUNDERS. In ICES FAST. 1-9 (ICES, 2004).
De Robertis, A. & Higginbottom, I. A post-processing technique to estimate the signal-to-noise ratio and remove echosounder background noise. ICES J. Mar. Sci. 64, 1282–1291, https://doi.org/10.1093/icesjms/fsm112 (2007).
Stanton, T. K. Effects of transducer motion on echo‐integration techniques. J. Acoust. Soc. Am. 72, 947–949, https://doi.org/10.1121/1.388175 (1982).
Dunford, A. J. Correcting echo-integration data for transducer motion. J. Acoust. Soc. Am. 118, 2121–2123, https://doi.org/10.1121/1.2005927 (2005).
ICES. Report of the Workshop on Collecting Quality Underwater Acoustic Data in Inclement Weather (WKQUAD). WKQUAD REPORT 2017 31 March - 2 April 2017. Nelson, New Zealand. ICES CM 2017/SSGIEOM:28. 1-27 (2017).
Mackenzie, K. V. Nine‐term equation for sound speed in the oceans. J. Acoust. Soc. Am. 70, 807–812, https://doi.org/10.1121/1.386920 (1981).
Francois, R. E. & Garrison, G. R. Sound absorption based on ocean measurements. Part II: Boric acid contribution and equation for total absorption. J. Acoust. Soc. Am. 72, 1879–1890, https://doi.org/10.1121/1.388673 (1982).
Ridgway, K. R., Dunn, J. R. & Wilkin, J. L. Ocean Interpolation by Four-Dimensional Weighted Least Squares—Application to the Waters around Australasia. J. Atmos. Oceanic Technol. 19, 1357–1375 https://doi.org/10.1175/1520-0426(2002)019%3C1357:OIBFDW%3E2.0.CO;2 (2002).
Ridgway, K. R., Coleman, R. C., Bailey, R. J. & Sutton, P. Decadal variability of East Australian Current transport inferred from repeated high-density XBT transects, a CTD survey and satellite altimetry. J. Geophys. Res. Oceans 113, https://doi.org/10.1029/2007JC004664 (2008).
Eaton, B. et al. NetCDF Climate and Forecast (CF) Metadata Conventions. Version 1.6 https://cfconventions.org/cf-conventions/v1.6.0/cf-conventions.pdf (2011).
IMOS. IMOS NETCDF CONVENTIONS. Version 1.4.1 http://content.aodn.org.au/Documents/IMOS/Conventions/IMOS_NetCDF_Conventions.pdf (2020).
ICES. A metadata convention for processed acoustic data from active acoustic systems. Series of ICES Survey Protocols SISP 4-TG-AcMeta., 1–47, https://doi.org/10.17895/ices.pub.7434 (2016).
Haris, K. et al. Bioacoustics data from Ships of Opportunity (2008–2020). Australian Ocean Data Network https://doi.org/10.26198/dv5p-t593 (2020).
Kieser, R., Mulligan, T. J., Williamson, N. J. & Nelson, M. O. Intercalibration of Two Echo Integration Systems based on Acoustic Backscattering Measurements. Can. J. Fish. Aquat. Sci. 44, 562–572, https://doi.org/10.1139/f87-069 (1987).
Downie, R. A., Kloser, R. J. & Ryan, T. E. An analysis of the IMOS BioAcoustic Ships of Opportunity Program calibration data 2010–2017. 1–35 (CSIRO, 2018).
Knudsen, H. P. Long-term evaluation of scientific-echosounder performance. ICES J. Mar. Sci. 66, 1335–1340, https://doi.org/10.1093/icesjms/fsp025 (2009).
ICES. Collection of acoustic data from fishing vessels. ICES Coop. Res. Rep. 287, 1–83, https://doi.org/10.17895/ices.pub.5452 (2007).
Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73, https://doi.org/10.1109/TAU.1967.1161901 (1967).
Haris, K., Kloser, R. J., Ryan, T. E. & Malan, J. Deep-water calibration of echosounders used for biomass surveys and species identification. ICES J. Mar. Sci. 75, 1117–1130, https://doi.org/10.1093/icesjms/fsx206 (2017).
Doonan, I. J., Coombs, R. F. & McClatchie, S. The absorption of sound in seawater in relation to the estimation of deep-water fish biomass. ICES J. Mar. Sci. 60, 1047–1055, https://doi.org/10.1016/S1054-3139(03)00120-6 (2003).
Macaulay, G. J., Chu, D. & Ona, E. Field measurements of acoustic absorption in seawater from 38 to 360 kHz. J. Acoust. Soc. Am. 148, 100–107, https://doi.org/10.1121/10.0001498 (2020).
De Robertis, A. et al. Amplifier linearity accounts for discrepancies in echo-integration measurements from two widely used echosounders. ICES J. Mar. Sci. 76, 1882–1892, https://doi.org/10.1093/icesjms/fsz040 (2019).
Bassett, C., Lavery, A. C., Stanton, T. K. & Cotter, E. D. Frequency- and depth-dependent target strength measurements of individual mesopelagic scatterers. J. Acoust. Soc. Am. 148, EL153–EL158, https://doi.org/10.1121/10.0001745 (2020).
Dias Bernardes, I., Ona, E. & Gjøsæter, H. Study of the Arctic mesopelagic layer with vessel and profiling multifrequency acoustics. Prog. Oceanogr. 182, 102260, https://doi.org/10.1016/j.pocean.2019.102260 (2020).
NOAA Office of Ocean Exploration and Research. EK60 Water Column Sonar Data Collected During EX1404L1. NOAA National Centers for Environmental Information https://doi.org/10.7289/V5ZW1HW0 (2014).
NOAA/NMFS Alaska Fisheries Science Center. EK60 Water Column Sonar Data Collected During DY1001. NOAA National Centers for Environmental Information https://doi.org/10.7289/V5C82772 (2010).
NOAA/NMFS Pacific Islands Fisheries Science Center. EK60 Water Column Sonar Data Collected During SE1102L2. NOAA National Centers for Environmental Information https://doi.org/10.7289/V53776PJ (2011).
NOAA/NMFS Southwest Fisheries Science Center. EK60 Water Column Sonar Data Collected During RL1705. NOAA National Centers for Environmental Information https://doi.org/10.7289/V50V8B37 (2017).
Acknowledgements
Funding for IMOS Bioacoustics sub-Facility was received from IMOS and CSIRO Oceans and Atmosphere. IMOS is enabled by the National Collaborative Research Infrastructure Strategy (NCRIS). It is operated by a consortium of institutions as an unincorporated joint venture, with the University of Tasmania as Lead Agent. The authors are grateful to all platform operators (Table 1) for generously contributing data to the program. Particularly, the commercial fishing companies Austral Fisheries, Australian Longline Pty Ltd, and Sealord Group Ltd were instrumental to foster existing ocean industry collaboration. Likewise, the National Institute of Water and Atmospheric Research (NIWA) and National Oceanic and Atmospheric Administration (NOAA) National Centers for Environmental Information (NCEI) were instrumental to foster scientific data sharing and reuse. We express our appreciation to the officers and crew in charge of the respective fishing trips and scientific voyages. The CSIRO managed Marine National Facility RV Investigator through the Geophysical Survey and Mapping (GSM) team provides ongoing support for data collections and instrument testing. We acknowledge Matt Boyd, CSIRO for performing RV Investigator calibrations. Benedicte Pasquer, AODN Project Officer provides timely assistance on many matters for managing data at the AODN Portal. Natalia Atkins, AODN Project Officer helped with the creation of ‘Data Citation’. Jake Wallis, IMOS Program Officer provided data illustration and relevant logos used in Fig. 1. Louise Bell helped with the generation of Fig. 2. Haley Viehman, Echoview® software Pty Ltd assisted to clarify data processing filters implemented in the software. We thank present and past members of ICES Working Group on Fisheries Acoustics, Science and Technology (WGFAST) for facilitating calibration standards, data quality measures, and metadata standards. This publication project was supported by CSIRO Oceans and Atmosphere and the European H2020 International Cooperation project Mesopelagic Southern Ocean Prey and Predators (MESOPP, http://www.mesopp.eu/).
Author information
Authors and Affiliations
Contributions
This publication is an outcome of collective contributions provided by all authors over 10 years of project development period. K.H.: data and metadata management, quality control and processing, liaise with AODN Project Officer, performed analyses, generated figures, and wrote the paper with inputs from all authors. R.J.K.: principal investigator of IMOS Bioacoustics sub-Facility, designed program, methods and metadata developments, reviewed quality-controlled data, and foster uptake of data products. T.E.R.: developed data processing methods, foster development of metadata convention for processed acoustic data, liaise with commercial fishing companies, and calibration. R.A.D.: calibration of vessels, data management, quality-controlled and processed data, and liaise with commercial fishing companies. G.K.: developed software packages for data management and processing. A.W.N.: quality control and processing of RV Investigator data.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files associated with this article.
About this article
Cite this article
Haris, K., Kloser, R.J., Ryan, T.E. et al. Sounding out life in the deep using acoustic data from ships of opportunity. Sci Data 8, 23 (2021). https://doi.org/10.1038/s41597-020-00785-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-020-00785-8
This article is cited by
-
Acoustic micronektonic distribution and density is structured by macroscale oceanographic processes across 17–48° N latitudes in the North Atlantic Ocean
Scientific Reports (2023)
-
Scientific echosounder data provide a predator’s view of Antarctic krill (Euphausia superba)
Scientific Data (2023)
-
Global decline of pelagic fauna in a warmer ocean
Nature Climate Change (2022)