Abstract
This manuscript describes an observationally-based dataset of soil evaporation for the conterminous U.S. (CONUS), gridded to a 9 km resolution for the time-period of April 2015-March 2019. This product is termed E-SMAP (Evaporation-Soil Moisture Active Passive) in which soil evaporation is estimated from the surface layer, defined by the SMAP sensing depth of 50 mm, between SMAP overpass intervals that are screened on the basis of precipitation and SMAP quality control flags. Soil evaporation is estimated using a water balance of the surface soil that we show is largely dominated by SMAP-observed soil drying. E-SMAP soil evaporation is on average 0.72 mm day−1, which falls within the range of soil evaporation estimates (0.17–0.89 mm day−1) derived from operational land surface models and an alternative remote sensing product. E-SMAP is independent from existing soil evaporation estimates and therefore has the potential to improve understanding of evapotranspiration partitioning and model development.
Measurement(s) | evaporation |
Technology Type(s) | satellite imaging • computational modeling technique |
Factor Type(s) | geographic location • temporal interval |
Sample Characteristic - Environment | soil |
Sample Characteristic - Location | United States of America |
Machine-accessible metadata file describing the reported data: https://doi.org/10.6084/m9.figshare.13181822
Similar content being viewed by others
Background & Summary
Evapotranspiration (ET) connects the surface water and energy budgets1. It is the second largest component of the terrestrial water balance after precipitation and is a source of feedback in the climate system2,3. Our ability to observe the return-flow of moisture from the land to the atmosphere is limited by sparse in situ observations that are not generally representative of regional scales4,5,6. Remotely sensed ET across a range of data products often have similar representations of ET’s seasonality2,7. However, these products show large dissimilarities7, in particular when water is the limiting factor for ET (e.g. during drought)2,8. In the absence of snow, ET is the sum of three components: 1) evaporation from the soil surface (Esoil), 2) transpiration from vegetation (ET), and 3) evaporation of intercepted water from vegetation canopies (EC). Partitioning of ET into these three components with models5,9,10 and remote sensing2 often reveal large disagreements. In this study, we apply the methodology developed by Small et al.11 to estimate soil evaporation using soil moisture drying rates observed by the Soil Moisture Active Passive (SMAP) satellite. This continental-scale gridded dataset is unique from other datasets and has the potential to improve the representation of ET partitioning in hydrologic models and climate studies.
Ground-based observational techniques, for example, the eddy covariance12 or Bowen Ratio energy balance methods13,14, provide measurements of the total ET flux. However, these ground-based observations only provide estimates of Esoil when ET is zero, for example when vegetation experiences seasonal senescence. Ground-based measurements can provide estimates of Esoil directly, such as weighing lysimeters15,16, and indirectly, such as the heat pulse method17,18. However, such ground-based observations of Esoil are labor intensive, and thus cannot be applied at the regional scale or for long-term monitoring15,16,17,18,19.
Land surface models (LSMs) compliment sparse ground-based monitoring of ET by producing spatially and temporally continuous estimates of total ET and its components. Yet, simulated fluxes are dependent on imperfect model structure and parameters that are difficult to estimate, resulting in large differences in Esoil estimates from different LSMs4,5,11. Total ET simulated by LSMs in the Global Land Data Assimilation System (GLDAS20), North American Land Data Assimilation System phase 2 (NLDAS-221,22) and experimental NLDAS-Testbed have been evaluated through comparison with remotely sensed ET23,24 and networks of eddy covariance flux towers11,25, but there has been no similar effort to evaluate Esoil, ET or Ec as few datasets exist for this purpose4,5. Without observationally-based estimates of how ET is partitioned into the component fluxes, it is not possible to improve the representation of Esoil, ET or Ec in hydrologic models.
Remote sensing provides a promising tool for estimating latent heat flux and evaluating simulated ET. Remote sensing methods that estimate ET largely rely on thermal data as a key input to the evapotranspiration algorithm26,27,28,29. However, these algorithms do not provide information about ET partitioning, only the total ET flux. Two exceptions being the Global Land Evaporation Amsterdam Model (GLEAM3,30) and the Priestly Taylor Jet Propulsion Laboratory (PT-JPL31,32) products, that provide estimates of total ET and its components. These realizations use remotely sensed soil moisture to inform estimates of Esoil, but both GLEAM and PT-JPL are strongly dependent on models that indirectly estimate ET and its components rather than direct measurements of evaporative flux (e.g. weighing lysimeters).
To address the above issues, we develop a new remote sensing-based dataset of Esoil over the conterminous United States (CONUS) from 2015–2019 that essentially uses SMAP as a giant lysimeter with a sensing scale equivalent to SMAP’s 9 km x 9 km footprint. This Evaporation-Soil Moisture Active Passive dataset (E-SMAP) is the first to use remotely sensed soil drying rates in a mass balance framework to estimate Esoil (Fig. 1), thus providing unique estimates of Esoil3,31. We extend the initial work of Small et al.11 that developed and evaluated E-SMAP at several in situ observation locations, to provide a continental-scale, 4-year, 9 km soil evaporation dataset. In this data descriptor, we first describe calculation of Esoil and a data screening procedure, followed by an exposition into the components of soil evaporation. Since there are no ‘true’ observations of continental-scale soil evaporation, the technical evaluation consists of comparisons between E-SMAP and another remote sensing Esoil product (GLEAM) as well as two LSM-based datasets from the NLDAS-2.
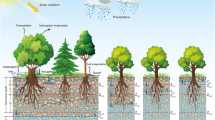
The water balance framework used to estimate soil evaporation. The E-SMAP approach is analogous to using SMAP as a lysimeter with a sensing scale equivalent to SMAP’s 9 km × 9 km footprint. Soil evaporation, Esoil, is estimated by Eq. 1 that accounts for fluxes in and out of a control volume (50 mm surface soil layer observed by SMAP). The direction of arrows represents the sign convention in Eq. 1 and the size of the arrow is proportional to the mean magnitude of each flux over intervals with minimal precipitation where E-SMAP records Esoil. The transpiration flux, ETs, only includes water extracted by roots in the surface layer.
Methods
Evaporation and the water balance of the surface soil layer
The procedure used to create E-SMAP follows the methodology described in Small et al.11. A brief summary is provided here, along with descriptions of alterations made to that approach. Esoil is estimated independently at each SMAP 9 km x 9 km grid cell via a water balance of the surface soil control volume (Fig. 1), where:
\({\theta }_{s}\) is volumetric soil moisture in the surface soil control volume (mm3mm−3), D is the thickness of the control volume (mm), qbot (mm day−1) is the flux across the bottom boundary of the control volume, ETs (mm day−1) is surface transpiration which is the fraction of total transpiration proportional to the fraction of roots within the top 50 mm surface soil layer, and I is infiltration (mm day−1). We define the thickness of the control volume, D, to be equivalent to the SMAP sensing depth (50 mm)33, noting that this sensing depth can vary through time with soil moisture34. We define qbot as positive when water moves from the control volume to deeper soil and negative when water moves from deeper soil to the control volume. Surface transpiration, ETs, is the fraction of total ET, proportional to the fraction of roots within the top 50 mm of the soil.
We use SMAP soil moisture time series to estimate Esoil following the assumption that Esoil is typically the largest flux in Eq. 1 excluding times when infiltration is actively occurring due to precipitation or snowmelt11. The observed \({\theta }_{s}\) time series is used to calculate \(\frac{d{\theta }_{s}}{dt}\) for intervals defined by successive SMAP overpasses35. The remaining terms on the right-hand side of Eq. 1 are estimated using a combination of auxiliary data and models described below.
Precipitation screening
Following Small et al.11, Eq. 1 is not applied to SMAP overpass intervals with substantial precipitation, since we seek to minimize uncertainties in the partitioning of incoming precipitation between runoff, canopy interception, and infiltration. Therefore, ‘valid intervals’ are defined as successive SMAP overpasses with less than 2 mm of precipitation, while those with larger precipitation values are considered ‘not valid’11. This threshold was selected to reflect SMAP’s accuracy and sensing depth33,36, where 2 mm of infiltrated water in a 50 mm soil column yields a soil moisture change equal to SMAP’s reported uncertainty (0.04 mm3mm−3). After screening for precipitation, 66% of SMAP’s overpasses remain valid (Fig. 2a).
Valid E-SMAP intervals and screening procedure. (a) E-SMAP’s spatial domain is shaded by the fraction of valid E-SMAP intervals on the basis of minimal precipitation (less than 2 mm). Land surface areas screened based on SMAP’s quality flag and Hydrus non-convergence are masked in white. (b) a histogram of valid E-SMAP interval durations. (c) an example time series to illustrate E-SMAP’s recording and screening procedure during one month over the Little Washita location. SMAP observations (black lines) are all at 6 AM local time. E-SMAP soil evaporation is coded at the midpoint of each E-SMAP interval (red dashed lines). E-SMAP intervals with more than 2 mm of cumulative precipitation are screened (grey shading). Drying rates are calculated from successive 6 AM SMAP observations bounding the E-SMAP interval, and other fluxes on the right-hand-side of Eq. 1 are estimated at finer time steps (hourly) and summed over the E-SMAP interval.
Bottom flux (qbot)
We use the Hydrus 1-D model37 to estimate qbot. Model inputs include soil properties that are defined using soil texture and top boundary conditions that are set to observed atmospheric boundary conditions (Table 1). The model solves the Richards’ equation for saturated and unsaturated conditions. Here, the modeled soil column depth was set to 1000 mm, discretized with 101 nodes evenly separated 10 mm apart. Model simulations were initialized with a 4 year run (April 1, 2015- March 31, 2019), where the outputs from March 31, 2019 of this spin-up were used to set initial soil moisture conditions in the Hydrus simulations used to calculate qbot for E-SMAP. The exchange of moisture below the 50 mm node represents the flux at the bottom boundary of the control volume, qbot. Small et al.11 quantified the uncertainty of qbot caused by soil parameter uncertainties to be less than 0.1 mm day−1 during valid intervals (<2 mm of total precipitation).
Transpiration from the surface soil layer (ETs)
We compute transpiration from the surface soil control volume for each grid cell based based on the calculation of total transpiration38. Using a modified version of the Penman-Monteith potential evapotranspiration (PET) equation39, potential transpiration is calculated accounting for fraction of the land surface covered by vegetation based on Enhanced Vegetation Index (EVI)40:
where λE is potential transpiration, s is the slope of the saturated water vapor pressure curve (Pa K−1), A is the net radiation (W m−2), \(\rho \) is air density (kg m−3), Cp is specific heat capacity of air (1005 J kg−1 K−1), esat-e is vapor pressure deficit, ra is aero dynamic resistance (s m−1), \(\gamma \) is the psychometric constant (Pa K−1), and rs is surface resistance. Fc is the fraction of total vegetation cover calculated as a function of EVI38 and Fwet is the relative surface wetness38. We then calculate ETs from λE by applying linear restrictions based on the fraction of total roots in the surface soil layer following an exponential function for root density41 as well as the surface soil water stress using observed soil moisture content from SMAP and soil properties42,43 in Eq. 3
where rf is the percent of roots in the top 50 mm of the surface soil column41 and FSM is the soil water stress, calculated following prior literature42,43 using Eq. 4
where θi is soil moisture at timestep i, θw is the wilting point of the soil and θcap is the field capacity of the soil.
Input data sources for calculation of ETs can be found in Table 1.
Infiltration (I)
I is assumed to be equivalent to precipitation during valid intervals, and is therefore expected to be overestimated since canopy interception is not considered. We do not expect this error source to significantly impact Esoil calculated over intervals with little or no precipitation because overestimates in I will largely cancel out with overestimates in downwards qbot which are estimated from Hydrus 1-D simulations that receive the same precipitation. This assumption may result in underestimation of Esoil during periods when I is driven by other sources, such as snowmelt. However, these errors are expected to negligibly impact E-SMAP because SMAP already includes screening flags for regions and times with frozen soil and substantial snow coverage (snow fraction exceeding 5%)44.
Data screening
Data are screened on the basis of precipitation (described above in the Precipitation Screening section) as well as through SMAP quality flags. SMAP’s retrieval quality flag is used to screen data that is not of “recommended quality”44. Screening on the basis of SMAP’s quality flags resulted in a reduction of nearly 40% of all SMAP grid cells in the study domain (118,531 to 72,105).
An additional constraint is the non-convergence of the Hydrus 1-D solver. 9,450 grid cells did not converge in Hydrus 1-D with the originally chosen soil parameter sets. To overcome the non-convergence, soil parameters at these grid cells were altered one of two ways: (1) parameters associated with the secondary soil classification at the grid cell were used or (2) if there was not a secondary soil classification, the NLDAS-2 “other” soil classification was used. Altering soil parameters resulted in convergence of 8,699 grid cells, while the remaining 751 points (0.6% of the domain) were ultimately screened from the dataset. Altering soil parameters is expected to have minimal impacts on calculations of Esoil because the uncertainty in qbot associated with soil parameters is much smaller than the magnitude of Esoil11. Finally, intervals with negative Esoil or ETs estimates were considered physically unrealistic and were also screened, reducing the E-SMAP space-time domain by 31%. The two primary reasons for negative Esoil outputs from Eq. 1 are (i) negative biases in SMAP observed drying rates and (ii) underestimates in precipitation (e.g. under-catch errors). The implications of this screening procedure as a whole are presented in the Technical Evaluation section.
Statistical testing
Statistical significance of a Pearson correlation reported in the Technical Evaluation section is calculated from a right-tailed significance test in MATLAB (https://www.mathworks.com/help/stats/corr.html). Statistical significance of the differences between medians that are reported in the Technical Evaluation section are calculated from paired one-tailed Wilcoxon signed rank tests using the exactRankTests R Library45.
Data Records
A list of data sources used to build E-SMAP are included in Table 1. Each data source is remapped to SMAP’s 9 km EASE-Grid with the nearest neighbor approach. As part of the E-SMAP dataset, gridded estimates are posted for each component in Eq. 1 on SMAP’s 9 km EASE-Grid from April 2015 through March 2019 during SMAP’s valid intervals (Table 2). The spatial domain encompasses 25°N–50°N and 125°W–67°W, covering the entire CONUS. The dataset, archived on Mendeley in netCDF format, is intended to support modeling development efforts that focus on the partitioning of ET into its components and climate case studies within the period of data record (2015–2019) that require independent representation of ET components. The dataset should be cited as: Abolafia-Rosenzweig, R., Badger, A., Small, E., Livneh, B. E-SMAP: Evaporation-Soil Moisture Active Passive. Mendeley https://doi.org/10.17632/ffw8zbdmpm.2 (2020)46.
E-SMAP is compared with one remote sensing-based and two LSM-based soil evaporation datasets in the “Technical Evaluation” (Table 3). The three evaluation datasets were remapped to SMAP’s 9 km EASE-Grid using bilinear interpolation from the CDO software47 prior to comparison with E-SMAP. No true ‘validation’ of E-SMAP was conducted because no continental-scale and spatially representative observations of Esoil exist. Thus, the technical evaluation examines similarities and differences of E-SMAP relative to widely used Esoil datasets rather than quantifying the accuracy of E-SMAP. A point scale evaluation of the E-SMAP methodology over 10 validation sites can be found in Small et al.11.
Technical Evaluation
Kernel density estimators are used to show the overall tendencies of E-SMAP components in Fig. 3b–g. Esoil is largely explained by SMAP drying rates, \(-\frac{d{\theta }_{s}}{dt}D\) and is modulated more modestly by other fluxes in Eq. 1 that are estimated from auxiliary data and models (qbot, I, and ETs). On average, for most regions, qbot is upwards into the surface control volume and largely ‘cancels out’ with ETs. Additionally, qbot, I, and ETs are each approximately four to five times smaller than SMAP drying rates. This results in the summation of qbot, I, and ETs to be, on average, four times smaller than drying rates observed by SMAP (Fig. 3).
E-SMAP Esoil relies more heavily on observed drying rates than ancillary data and models. (a) Median SMAP drying rates divided by Esoil over the E-SMAP domain. Kernel density estimators for each water balance component in Eq. 1 for the (b) Northwest, (c) Midwest, (d) Northeast, (e) Southwest, (f) Great Plains and (g) Southeast. Data presented in panels a–g are representative of all time steps for each region in the E-SMAP data set.
The median ratio between SMAP drying rates and Esoil (Fig. 3a) is used to quantify the central tendency of the fraction of the Esoil signal attributable to SMAP drying rates. For example, in the Midwest, this fraction is 0.85, thus the summation of components estimated from ancillary data and tools (qbot, I, and ETs) composes 15% of the Esoil signal. E-SMAP relies on ancillary data and models more heavily where the ratio of SMAP drying to Esoil is substantially less than 1.0. For example, in the Northwest this ratio is approximately 0.77. There is a statistically significant correlation (p < 0.01; R2 = 0.91) between mean regional drying rates and the ratio of drying rates divided by Esoil, supporting the interpretation that where the SMAP drying rates are relatively large, qbot, I and ETs play smaller roles in the Esoil calculation. Overall, Fig. 3 supports that variability of Esoil in E-SMAP is primarily explained by SMAP drying rates, with contributions from other estimates ranging from 2% (Northeast) to 23% (Northwest).
We seek to understand the implications of data screening on the magnitude of Esoil to evaluate the representativeness of the screened E-SMAP product on climatological conditions. We compare a screened version of each evaluation product, matching E-SMAP’s temporal sampling produced from screening, with corresponding temporally continuous estimates (Fig. 4). All evaluation datasets show that E-SMAP screening results in a statistically significant increase (p < 0.01) in the central tendency of mean monthly Esoil (Fig. 4) and Esoil/ET (not shown). Evaluation products’ Esoil averaged over valid E-SMAP intervals are larger than corresponding continuous estimates, on average, by 9%, 10% and 2%, while Esoil/ET is larger by 3%, 17% and 8% for GLEAM, Mosaic and Noah, respectively. Figure 4d shows the interquartile range for the ratio of Esoil from screened time series relative to continuous time series is 1.05–1.12, 1.06–1.14, and 1.00–1.05 for GLEAM, Mosaic and Noah, respectively.
Impact of E-SMAP screening on the magnitude of Esoil. The ratio of mean monthly Esoil for valid intervals (after screening) divided by continuous estimates from (a) GLEAM, (b) Mosaic, and (c) Noah. (d) Box plot of mean monthly Valid Esoil/Continuous Esoil, where each whisker is the length of the interquartile range.
Screening based on negative E-SMAP Esoil results in higher monthly Esoil in all evaluation datasets, whereas precipitation screening results in higher Esoil in GLEAM and Mosaic but lower Esoil from Noah. Precipitation screening results from GLEAM and Mosaic contradict the hypothesis that Esoil is higher over rainy intervals. Therefore, these results may indicate that Noah more accurately represents Esoil relative to GLEAM and Mosaic. However, further analysis into this disagreement is outside the scope of this data descriptor. Regardless, the effect of precipitation screening in reducing Noah Esoil is outweighed by increases corresponding with negativity screening. In sum, all evaluation products show higher Esoil after following the E-SMAP screening procedure. Thus, on average, the E-SMAP product is expected to represent a modest, but significantly higher, monthly Esoil and Esoil/ET than temporally continuous estimates, notwithstanding large spatial and temporal variability noted in Fig. 4. We therefore include temporally static, gridded scaling factors with the E-SMAP dataset—calculated as the ratio of mean monthly continuous Esoil time series divided by mean monthly screened time series from evaluation datasets—that may be multiplied with E-SMAP’s final Esoil to estimate average temporally continuous Esoil over the 4-year E-SMAP period. Key to the application of these scaling factors is the assumption that Esoil estimated from Eq. 1 is affected by scaling factors similar to evaluation products.
Esoil from E-SMAP falls within the range of the evaluation products (Fig. 5). Comparing mean values of Esoil, E-SMAP is on average 0.72 mm day−1, which is larger than GLEAM (0.17 mm day−1) and Noah (0.5 mm day−1) but smaller than Mosaic (0.89 mm day−1). E-SMAP Esoil has a lower R2 with GLEAM, Mosaic and Noah (0.16, 0.13 and 0.15, respectively; not shown) than correlations between the GLEAM and the LSM evaluation datasets (R2 = 0.48 and 0.52 with Mosaic and Noah, respectively), which may be reflective of E-SMAP’s independence from these datasets. Reduced correlations are also partially attributable to the SMAP drying rates themselves, which are expected to be unbiased but contain random noise that may exceed the magnitude of Esoil in some cases32. This noisiness would correspond with a noisy Esoil estimate with reduced correlation relative to evaluation datasets, but with more stable averages over seasonal or longer time periods. Overall, Esoil from E-SMAP is comparable with Esoil from the evaluation datasets but caution should be exercised with individual data points because the effect of random noise within SMAP drying rates.
Esoil from E-SMAP is greater than Noah and GLEAM but smaller than Mosaic. (a) Mean E-SMAP Esoil over the domain. (b) Kernel density estimators of mean Esoil from all locations calculated for E-SMAP, Mosaic, Noah and GLEAM. Vertical dashed lines represent median values. Spatial differences are expressed in mm day−1 between E-SMAP and (c) GLEAM, (d) Mosaic and (e) Noah.
Usage Notes
Moisture flux estimates in the E-SMAP dataset represent the average flux over the valid SMAP interval and are reported at the mid-date of respective intervals. The E-SMAP dataset may be used to estimate soil evaporation over a time period of months or years. However, soil evaporation estimates at individual time steps should be used with caution because unbiased uncertainty in observed drying rates from the SMAP satellite will introduce noise into shorter-interval estimates.
Code availability
All scripts are accessible here: https://github.com/RAbolafiaRosenzweig/ESMAP. R code was used for the calculations of each component in Eq. 1 and gridding outputs from individual pixels to the E-SMAP grid. MATLAB was used to produce the final data product and conduct the technical validation. Further, processing of the data in network Common Data Form (netCDF) format was done for remapping and aggregating using the open source Climate Data Operators (CDO) and netCDF Operator (NCO) utilities. Hydrus-1D simulations were performed with publicly available model code (https://github.com/bilke/hydrus).
References
Bastiaanssen, W. G. M. et al. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. Journal of Irrigation and Drainage Engineering 131, 85–93 (2005).
Miralles, D. G. et al. The WACMOS-ET project – Part 2: Evaluation of global terrestrial evaporation data sets. Hydrology and Earth System Science 20, 823–842 (2016).
Miralles, D. G. et al. Global land-surface evaporation estimated from satellite-based observations. Hydrology and Earth System Science 15, 453–469 (2011).
Kumar, S., Holmes, T., Mocko, D., Wang, S. & Peters-Lidard, C. Attribution of flux partitioning variations between land surface models over the Continental U.S. Remote Sensing 10, 751 (2018).
Lawrence, D. M., Thornton, P. E., Oleson, K. W. & Bonan, G. B. The partitioning of evapotranspiration into transpiration, soil evaporation, and canopy evaporation in a GCM: Impacts on land–atmosphere interaction. Journal of Hydrometeorology 8, 862–880 (2007).
Rodell, M., McWilliams, E. B., Famiglietti, J. S., Beaudoing, H. K. & Nigro, J. Estimating evapotranspiration using an observation based terrestrial water budget. Hydrological Processes 25, 4082–4092 (2011).
Jiménez, C. et al. Global intercomparison of 12 land surface heat flux estimates. Journal of Geophysical Research. 116, D02102 (2011).
Dolman, A. J. & de Jeu, R. A. M. Evaporation in focus. Nature Geoscience 3, 296–296 (2010).
Dirmeyer, P. A. The land surface contribution to the potential predictability of boreal summer season climate. Journal of Hydrometeorology 6, 618–632 (2005).
Choudhury, B. J. & Monteith, J. L. A four-layer model for the heat budget of homogeneous land surfaces. Quarterly Journal of the Royal Meteorological Society 114, 373–398 (1988).
Small, E., Badger, A., Abolafia-Rosenzweig, R. & Livneh, B. Estimating soil evaporation using drying rates determined from satellite-based soil moisture records. Remote Sensing 10, 1945 (2018).
Baldocchi, D. et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities. Bulletin of the American Meteorological Society 82, 2415–2434 (2001).
Robock, A. et al. Evaluation of the North American Land Data Assimilation System over the southern Great Plains during the warm season. Journal of Geophysical Research 108 (2003).
Spittlehouse, D. L. & Black, T. A. Evaluation of the Bowen ratio/energy balance method for determining forest evapotranspiration. Atmosphere-Ocean 18, 98–116 (1980).
Shawcroft, R. W. & Gardner, H. R. Direct evaporation from soil under a row crop canopy. Agricultural Meteorology 28, 229–238 (1983).
Herbst, M., Kappen, L., Thamm, F. & Vanselow, R. Simultaneous measurements of transpiration, soil evaporation and total evaporation in a maize field in northern Germany. Journal of Experimental Botany 47, 1957–1962 (1996).
Heitman, J. L., Horton, R., Ren, T., Nassar, I. N. & Davis, D. D. A test of coupled soil heat and water transfer prediction under transient boundary temperatures. Soil Science Society of America Journal 72, 1197 (2008).
Xiao, Z., Lu, S., Heitman, J., Horton, R. & Ren, T. Measuring subsurface soil-water evaporation with an improved heat-pulse probe. Soil Science Society of America Journal 76, 876–879 (2012).
Stannard, D. I. & Weltz, M. A. Partitioning evapotranspiration in sparsely vegetated rangeland using a portable chamber. Water Resources Research 42 (2006).
Rodell, M. et al. The Global Land Data Assimilation System. Bulletin of the American Meteorological Society 85, 381–394 (2004).
Xia, Y. et al. Continental-scale water and energy flux analysis and validation for North American Land Data Assimilation System project phase 2 (NLDAS-2): 2. Validation of model-simulated streamflow. Journal of Geophysical Research 117 (2012a).
Xia, Y. et al. Continental-scale water and energy flux analysis and validation for the North American Land Data Assimilation System project phase 2 (NLDAS-2): 1. Intercomparison and application of model products. Journal of Geophysical Research: Atmospheres 117 (2012b).
Gellens-Meulenberghs, F., Arboleda A., & Ghilain N.. Towards a continuous monitoring of evapotranspiration based on MSG data, Proceedings of the IAHS Symposium on Remote Sensing for Environmental Monitoring and Change Detection, Perugia, Italy, IAHS Press, Wallingford, ROYAUME-UNI, (2007).
LSA-SAF. LSA-SAF validation report, Products LSA-16 (MET), LSA-17 (DMET), The EUMETSAT Network of Satellite Application Facilities, Document Number: SAF/LAND/RMI/VR/0.6, (2010).
Zhang, B. et al. Evaluation and comparison of multiple evapotranspiration data models over the contiguous United States: Implications for the next phase of NLDAS (NLDAS-Testbed) development. Agricultural and Forest Meteorology 280, 107810 (2020).
Kustas, W. P. & Norman, J. M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agricultural and Forest Meteorology 41, 13–29 (1999).
Allen, R. G. et al. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Applications. Journal of Irrigation and Drainage Engineering 133, 395–406 (2007).
Anderson, M. C. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sensing of Environment 60, 195–216 (1997).
Bastiaanssen, W. G. M., Menenti, M., Feddes, R. A. & Holtslag, A. A. M. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. Journal of Hydrology 212–213, 198–212 (1998).
Martens, B. et al. GLEAM v3: satellite-based land evaporation and root-zone soil moisture, Geoscientific Model. Development 10, 1903–1925 (2017).
Fisher, J. B., Tu, K. P. & Baldocchi, D. D. Global estimates of the land–atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sensing of Environment 112, 901–919 (2008).
Purdy, A. J. et al. SMAP soil moisture improves global evapotranspiration. Remote Sensing of Environment 219, 1–14 (2018).
Entekhabi, D. et al. SMAP Handbook; Laboratory, J.P., Ed.; JPL Publication JPL 400–1567; NASA CalTech: Pasadena, CA, USA (2014).
Njoku, E. G. & Kong, J.-A. Theory for passive microwave remote sensing of near-surface soil moisture. Journal of Geophysical Research 82, 3108–3118 (1977).
Shellito, P. J. et al. SMAP soil moisture drying more rapid than observed in situ following rainfall events. Geophysical Research Letters 43, 8068–8075 (2016).
Colliander, A. et al. Validation of SMAP surface soil moisture products with core validation sites. Remote Sensing of Environment 191, 215–231 (2017).
Šimůnek, J., Jarvis, N. J., van Genuchten, M. Th & Gärdenäs, A. Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. Journal of Hydrology 272, 14–35 (2003).
Mu, Q., Zhao, M. & Running, S. W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sensing of Environment 115, 1781–1800 (2011).
Monteith, J. L. Evaporation and environment. Symposium of the society of experimental biology 19, 205–224 (1965).
Didan, K.; Barreto Munoz, A.; Solano, R.; Huete, A. MODIS vegetation index user’s guide; collection 6; NASA: Washington, DC, USA (2015).
Zeng, X. Global vegetation root distribution for land modeling. Journal of Hydrometeorology 2, 6 (2001).
Peters-Lidard, C. D., Zion, M. S. & Wood, E. F. A soil-vegetation-atmosphere transfer scheme for modeling spatially variable water and energy balance processes. Journal of Geophysical Research: Atmospheres 102, 4303–4324 (1997).
Jacquemin, B. & Noilhan, J. Sensitivity study and validation of a land surface parameterization using the HAPEX-MOBILHY data set. Boundary-Layer Meteorology 52, 93–134 (1990).
O’Neill, P., Chan, S., Njoku, E., Jackson, T., & Bindlish, R. Algorithm theoretical basis document level 2 & 3 Soil Moisture (Passive) data products, Revision D, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, California. JPL D-66480 (2018).
Torsten Hothorn and Kurt Hornik. exactRankTests: Exact Distributions for Rank and Permutation Tests. R package version 0.8–29. https://CRAN.R-project.org/package=exactRankTests (2017).
Abolafia-Rosenzweig, R., Badger, A., Small, E. & Livneh, B. E-SMAP: Evaporation-Soil Moisture Active Passive. Mendeley Data https://doi.org/10.17632/ffw8zbdmpm.2 (2020).
Schulzweida, Uwe. CDO User Guide (Version 1.9.8). Zenodo https://doi.org/10.5281/zenodo.3539275 (2019).
O’Neill, P. E., Chan, S., Njoku, E. G., Jackson, T. & Bindlish, R. SMAP enhanced L3 radiometer global daily 9 km EASE-grid soil moisture, Version 1; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA (2016).
NCEP/EMC. NLDAS Primary Forcing Data L4 Hourly 0.125 x 0.125 Degree V002; Goddard Earth Sciences Data and Information Services Center (GESDISC): Greenbelt, MD, USA (2009).
Hansen, M., DeFries R., Townshend J. R. G. & Sohlberg R. UMD global land cover classification, 1 kilometer, 1.0, Department of Geography, University of Maryland, College Park, Maryland, 1981–1994 (1998).
Hansen, M. C., Defries, R. S., Townshend, J. R. G. & Sohlberg, R. Global land cover classification at 1 km spatial resolution using a classification tree approach. International Journal of Remote Sensing 21, 1331–1364 (2000).
Miller, D. & White, R. A conterminous United States multilayer soil characteristics dataset for regional climate and hydrology modeling. Earth Interactions 2, 1–26 (1998).
Chen, F. & Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Monthly Weather Review 129, 17 (2001).
Acknowledgements
This research was funded by the National Aeronautics and Space Administration: NASA Grant # 80NSSC18K0951: A Remotely Sensed Ensemble to Understand Human Impacts on the Water Cycle and NASA Grant # NNX16AQ46G: Monitoring soil evaporation using SMAP surface soil moisture in a water balance framework. This work utilized the RMACC Summit supercomputer, which is supported by the National Science Foundation (awards ACI-1532235 and ACI-1532236), the University of Colorado Boulder, and Colorado State University. The Summit supercomputer is a joint effort of the University of Colorado Boulder and Colorado State University. Publication of this article was funded by the University of Colorado Boulder Libraries Open Access Fund.
Author information
Authors and Affiliations
Contributions
Ronnie Abolafia-Rosenzweig developed the dataset, curated data, performed technical validation, led data visualization and writing. Andrew M. Badger aided development of the dataset, data curation, and reviewing and editing the manuscript. Eric E. Small and Ben Livneh co-led conceptualization, methodology development, funding acquisition, project administration and supported writing review and editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files associated with this article.
About this article
Cite this article
Abolafia-Rosenzweig, R., Badger, A.M., Small, E.E. et al. A continental-scale soil evaporation dataset derived from Soil Moisture Active Passive satellite drying rates. Sci Data 7, 406 (2020). https://doi.org/10.1038/s41597-020-00748-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-020-00748-z
This article is cited by
-
The Effects of Groundwater Depth on the Soil Evaporation in Horqin Sandy Land, China
Chinese Geographical Science (2021)