Abstract
This dataset consists of 33 years (1985 to 2018), of global significant wave height and wind speed obtained from 13 altimeters, namely: GEOSAT, ERS-1, TOPEX, ERS-2, GFO, JASON-1, ENVISAT, JASON-2, CRYOSAT-2, HY-2A, SARAL, JASON-3 and SENTINEL-3A. The altimeter data have been calibrated and validated against National Oceanographic Data Center (NODC) buoy data. Differences between altimeter and buoy data as a function of time are investigated for long-term stability. A cross validation between altimeters is also carried out in order to check the stability and consistency of the calibrations developed. Quantile-quantile comparisons between altimeter and buoy data as well as between altimeters are undertaken to test consistency of probability distributions and extreme value performance. The data were binned into 1° by 1° bins globally, to provide convenient access for users to download only the regions of interest. All data are quality controlled. This globally calibrated and cross-validated dataset provides a single point of storage for all altimeter missions in a consistent format.
Design Type(s) | data integration objective • modeling and simulation objective |
Measurement Type(s) | environmental system process |
Technology Type(s) | Altimeter Device |
Factor Type(s) | temporal_interval • geographic location |
Sample Characteristic(s) | Earth (Planet) • ocean |
Machine-accessible metadata file describing the reported data (ISA-Tab format)
Similar content being viewed by others
Background & Summary
Satellite Radar altimeters have provided global coverage of wind speed and significant wave height (wave height) for more than three decades. Such data have been used for many applications, including: offshore engineering design, validation of numerical models, wind and wave climatology and investigation of long-term trends in oceanographic wind speed and wave height1,2,3,4,5. Since the launch of GEOSAT in 1985, there has been an almost continuous coverage of global observations from satellite altimeters. Following the conclusion of the GEOSAT mission in late-1989, there was a short gap until the launch of the European Remote-Sensing Satellite (ERS-1) in mid-1991. Since then, a total of 13 satellite altimeter missions have been operated, with the two latest launches, namely JASON-3 and SENTINEL-3A in 2016. The vast majority of these satellites have been placed in near-polar, sun-synchronous orbits. Altimeters are nadir-looking instruments, meaning they measure along a narrow, pencil-beam directly below the satellite (foot print approx. 10 km wide). This orbit geometry means that the satellites trace-out “herring bone” ground track patterns. Along track resolution of altimeter data is high, with data available at approximately 1 Hz along track (7 km). The ground track separation depends on orbit geometry but can be up to 400 km at the equator, with satellites repeating the same ground tracks on a 3 to 10 day repeat cycle (note that CRYOSAT-2 has a 369 day repeat cycle with a semi-repeat cycle of 30 days). In recent years, as the number of altimeters in operation has increased, the density of observations has greatly improved.
As a number of agencies have been responsible for the launch and operation of these satellites, data tends to be available from a relatively large number of sites, has been calibrated in a variety of different manners and exists in a variety of data formats. As this obviously complicates usage of the data, a number of attempts have been made to both consistently calibrate altimeter missions but also to provide data repositories for multiple missions. These include: Globwave (http://globwave.ifremer.fr/), Radar Altimeter Data System (RADS, http://rads.tudelft.nl, AVISO (https://www.aviso.altimetry.fr), National Satellite Ocean Application Service (NSOAS, http://www.nsoas.org.cn/) and National Oceanic and Atmospheric Administration (NOAA, https://www.noaa.gov/). However, none of these repositories archives all the missions over the period since 1985 in a consistent manner.
This paper outlines an archive containing wind speed and wave height data, together with related quantities for all 13 altimeter missions. The data are consistently calibrated against buoys, cross-validated between satellites and quality controlled. The satellite calibrations are checked for long term stability, discontinuities and drift. Should any of these occur, they are corrected. Previous satellite data repositories have all stored data along track, following the satellite orbit. Although this format provides a chronological archive of the data, it is generally not optimal for many users. Here, the data are archived in 1° by 1° bins. Within each bin, full data resolution is provided with all parameters for each 1 Hz observation provided (e.g. latitude, longitude, wind speed, wave height, quality flags etc). This binned storage, provides a convenient archiving arrangement for the large datasets, particularly for applications related to specific locations.
This paper describes the calibration, validation, quality control and archiving formats of this comprehensive database. The intention is for the dataset to be dynamic and to grow as future altimeter data become available. It is intended to be updated approximately every six months. This ongoing IMOS (Integrated Marine Observing System) Surface Waves Sub-Facility Altimeter Wave/Wind database is available through the Australian Ocean Data Network portal (AODN: https://portal.aodn.org.au/) the main repository for marine data in Australia. Users can search for the database by entering the search keywords “Altimeter waves” and data can be downloaded using the graphical user interface. The data can be accessed directly from:
A snapshot of the database at the time of this publication has been assigned a DOI and will be maintained in perpetuity by the AODN6. Detailed instructions for accessing the data are provided in the Data Records section below.
Methods
The calibration and validation methods described below build on the approach adopted by Young et al.7. The present dataset is, however, much expanded to include more recent altimeter missions. All data have been reprocessed so as to be consistent over the full 33-year data record.
In situ measurements
In order to calibrate the altimeters in a consistent fashion, a long-term high-quality database of buoy in situ measurements of wind speed and wave height is required. These data should span a range of different meteorological environments and geographic regions. In addition, such data should be relatively far from land, so as to avoid contamination of altimeter measurements due to land/islands within the altimeter footprint. The only in situ dataset which meets these requirements is the National Data Buoy Center (NDBC) buoy archive. Once NDBC data have been quality controlled, the data are archived by the National Oceanographic Data Center (NODC) and are available in the public domain. As with any long term in situ data archive of this type there have been changes in buoy hulls, instrumentation packages and analysis methods over the duration of the measurements8. The impact of such changes has previously been investigated in the context of trend estimates9. In the present application, data from a large number of buoys are pooled and a mean calibration obtained across all buoys. This process ensures that impacts resulting from the changes in hull type at specific locations have a negligible impact on the overall calibration result. The desire to have a long duration dataset relatively far offshore means that the data will be almost exclusively northern hemisphere. Although this will bias mean climatic conditions to some extent, it is unlikely to have a significant impact on the mean calibration10. Also, some doubts have been raised about the validity of such data at high wind speeds and wave heights3,4,8,11,12,13,14. Despite these concerns, the NDBC in situ dataset has been extensively used to validate model results and calibrate satellite systems and been found to be of high quality15,16.
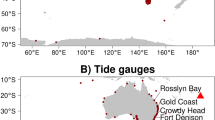
In this work, wind speed and significant wave height have been obtained from NODC moored buoy data more than 50 km offshore to avoid land contamination17. From 2011, NODC data contain a series of quality flags for wind speed and significant wave height (0, 1, 2, and 3 which represent quality_good, out_of_range, sensor_nonfunctional, and questionable, respectively). Only wind speed and significant wave height which are flagged “0” have been used for calibration of the altimeter data. The locations of NODC buoys used in the calibration are shown in Fig. 1.
The buoys measure either significant wave height (Hs), wind speed at the height of the anemometer z (Uz) or both. For wind speed, a consistent reference height of 10 m is required (U10). This was obtained by assuming a neutral stability logarithmic boundary layer as given by1:
where κ is the von Kármán constant which is approximately 0.4, Cd is the drag coefficient and zo is the roughness length. Measurements of Cd over the ocean yield results with scatter over an order of magnitude, and much research has focused on the wind speed and sea state dependence of Cd1,18,19. In this work, Cd = 1.2 × 10−3 and zo = 9.7 × 10−5 m are used. As mentioned in previous studies7, a different assumption of Cd does not have a significant influence on the final satellite wind speed17. For a more detailed description of NOAA buoy data, one can refer to Zieger20. This choice of boundary layer correction is consistent with previous altimeter calibrations17.
Altimeter data
The altimeter data used in this database were sourced from three different archived locations, namely Globwave21, Radar Altimeter Data System (RADS)22, and National Satellite Ocean Application Service (NSOAS)23. A total of 13 satellite missions: GEOSAT, ERS-1, TOPEX, ERS-2, GEOSAT Follow-On (GFO), JASON-1, ENVISAT, JASON-2, CRYOSAT-2, Hai Yang-2A (HY-2A), Satellite with ARgos and ALtika (SARAL), JASON-3 and SENTINEL-3A (expressed in the order of launch) were included. The duration of the combined altimeter missions is 33 years, from 1985 until 2018 except for the short break from 1990 until the middle of 1991 as shown in Fig. 2.
The data from six altimeters which were mostly retired before 2013, namely GEOSAT, ERS-1, TOPEX, ERS-2, GFO, and ENVISAT were obtained from Globwave. The calibration and validation of these altimeters has previously been described, using essentially the same process adopted here7. These altimeters were re-calibrated for the present database, resulting in very minor changes to the calibration relationships.
Data for a further six altimeters: JASON-1, JASON-2, CRYOSAT-2, SARAL, JASON-3 and SENTINEL-3A were obtained from RADS. The final satellite is Hai Yang-2A (HaiYang means ocean in Chinese). This satellite is China’s first dynamic environmental satellite and the data from this altimeter is not available in the public domain. However, following personal communication, the data were provided from NSOAS. Summary information for each of the satellites/altimeters is included in Table 1.
Values of significant wave height and wind speed are determined from the high frequency altimeter data by fitting a functional form to the radar return from the ocean surface in a process called waveform retracking. As noted above, the original data for the present database were sourced from Globwave, RADS and NSOAS. In the case of both Globwave24 and RADS25, these data were originally sourced from the various satellite agencies in the form of 1 Hz Geophysical Data Records (GDRs). The processing used to form the GDRs uses a range of different retracking approaches and no attempt has been made to harmonize the retracking. Rather, we use the 1 Hz data from the GDRs and calibrate at this level. This calibration clearly removes some differences between various datasets. A harmonized retracking of all data would presumably further increase the quality of data but is beyond the scope of this database.
Altimeter quality controls
Altimeter, Geophysical Data Records are not free from data errors and such data contain numerous data “spikes” due to land and ice contamination and issues associated with variable quality of the altimeter waveform received by the satellite17. As indicated previously7, the Globwave data contains a series of quality flags (0, 1, and 2, representing good_measurement, acceptable_for_some_applications, and bad_measurement, respectively)24. These flags proved very reliable in excluding poor quality data.
In the present database, a series of data flags defined as 1, 2, 3, 4, and 9 represent Good_data, Probably_good_data, SAR-mode data or possible hardware error (only used for CRYOSAT-2), Bad_data and Missing_data, respectively, have been used. Hence, the quality flags from Globwave have been transformed from flags 0, 1 and 2 to the present flags 1, 2 and 4. Moreover, all NaN values in Globwave have been defined as missing data which are flagged 9.
The RADS and NSOAS data do not have a similar system of quality flags. Hence, the following criteria have been used to assess the quality of the data. This approach is similar to that adopted previously17,26. Initially the Hs data are considered:
-
(1)
If Hs > 30 m, then the data point was flagged “4” which means “bad” data.
-
(2)
All points identified as over land and ice using land/ice masks (as defined in GDRs distributed with the original data by the various satellite agencies) were discarded.
-
(3)
In the present dataset, 1 Hz values are used. However, the satellite agencies do distribute data related to variability of 20 Hz products in the GDRs. All data in which the standard deviation of these 20 Hz altimeter data values is greater than 2.5 m signifies data where there is significant variability within the footprint and were flagged “4”.
-
(4)
After applying these quality controls, the data were divided into blocks of 25 points, which represents approximately 180 km along the ground track. As argued in Zieger et al.17, this represents segments long enough to form reliable statistics but not so long that data will not be coherent. Individual values in the block were identified as outliers, and flagged “4”, based on the median absolute deviation (MAD)27. The MAD is defined as28:
$$MAD=b\,median\left\{\left|\,{x}_{i}-{M}_{n}\,\right|\right\},$$where \({M}_{n}=median\left\{{x}_{i}\right\}\) and xi is the original observation in which i = 1, 2, 3, … n. In this case n = 25. The value of b is given by 1.4826 which is the scaling factor of Gaussian distributions29. Furthermore, following Miller30, a threshold value of 3 has been chosen and hence all values which are outside the following criterion were categorized as outliers27. The criterion is given by
$${M}_{n}-3\times MAD < {x}_{i} < {M}_{n}+3\times MAD.$$This equation can be rewritten as:
$$\left|\frac{{x}_{i}-{M}_{n}}{MAD}\right| < 3.$$ -
(5)
In a final check, blocks identified in test 4 above, were further considered. These blocks were re-divided into sub-blocks, either side of flagged points. These sub-blocks were considered in the following manner:
-
Each sub-block was examined for outliers, as in test 4, with any further points failing the test flagged as erroneous (“4”).
-
If the ratio \(R={\sigma }_{{H}_{s}}\left(block\right)/{\bar{H}}_{s}\left(block\right)\) is large, where \({\sigma }_{{H}_{s}}(block)\) is the standard deviation of the block and \({\bar{H}}_{s}(block)\) is the mean of the block, then it indicates that it is possible that there are multiple spikes in the block. If R > 0.5, then the entire sub-block was flagged as “4”.
The steps undertaken at points 4 and 5 above are intended to flag erroneous “spikes” in the data. Visual examination of many cases indicated it was remarkably successful at this, whilst not removing strong along-track gradients which may be caused by strong currents31,32. Nevertheless, the data are retained and flagged as “4”. Users interested in along-track variability can process such data if desired.
Similar criteria have been applied for wind speed (U10). In this case, for test 1 the wind speed limit was set at 60 ms−1 for all altimeters except SARAL. In the case of SARAL this limit was set at 24 ms−1. (See discussion of SARAL calibration below.) As for significant wave height, wind speed values above these limits were classified as “bad” data which are flagged “4”.
Calibration against in situ measurements
The quality controlled significant wave height and wind speed data were calibrated by comparing the buoy measurements with altimeter passes. Buoy observations and altimeter passes were considered a “matchup” if they satisfied the following criteria:
-
a.
Altimeter track was within 50 km of the buoy and the overpass occurred within 30 min. of the buoy recording data. These matchup criteria have been widely used in previous studies17,33,34,35,36,37,38.
-
b.
Only buoys which are more than 50 km offshore have been considered in order to avoid the impact of the proximity of land on both buoy and satellite observations.
-
c.
A minimum of five points were required in the altimeter pass within the 50 km radius region around the buoy.
-
d.
Any large variability in the along-track altimeter data was excluded. Specifically, passes in which \(\sigma \left({H}_{s}\right)/{\bar{H}}_{s} > 0.2\) were excluded, where σ(Hs) and \({\bar{H}}_{s}\) are the standard deviation and mean of values of the altimeter data within the 50 km radius region around the buoy.
Again, the same criteria were also applied for wind speed. As not all buoys measure both wind speed and wave height, there is not a one to one overlap between buoys used to calibrate wind speed and wave height.
The values of significant wave height (Hs) for calibration can be extracted directly from the various data archives. However, altimeter U10 is calculated from the radar cross-section, σ0 (ratio of the returned to transmitted energy of the altimeter pulse) and a variety of different relationships have historically been used for different altimeters. In order to have consistent calibrations across the various altimeters, it is desirable to use a consistent U10 − σ0 relationship7,17. Hence, following the method used in Zieger et al.17 and Young et al.7, uncalibrated wind speed was calculated based on the backscatter coefficient σ0 using the algorithm39:
where
The values of \(\alpha ,\,\beta ,\,\gamma ,\,\delta ,\,and\,{\sigma }_{b}\) in equation (3) are given by
Note that the units of wind speed in the above relationships are meters per second and the radar backscatter decibels.
Equations (2) and (3) with the value of the parameters given in (4) have been developed for Ku-band radar altimeters (13.5–13.8 GHz). The SARAL altimeter, however, is a Ka-band radar altimeter (35.75 GHz). Following Lillibridge et al.40 for calibrated Ka altimeters, (2) and (3) still hold but with the coefficients in (4) given by:
In addition, for high wind speed where U10 > 18 ms−1, a modified relationship41 has been adopted which is given by
This high wind speed relationship has recently been validated for use in extreme value analyses42. Quilfen et al.43 also obtained a very similar result to Eq. (6). There is some evidence that altimeter wind speed may be a function of sea state in addition to radar cross-section44. The analysis here does not consider any sea state dependence, which appears small.
Values of radar cross-section (σ0) provided for each of the altimeter systems have a variety of different datum offsets. Therefore, following Young et al.7, it is necessary to remove this offset before applying (3)–(6). This is achieved by comparing buoy measurements of U10 with altimeter σ0 and determining the offset σoffset which gives the best fit (in a least-squares sense) between the data and (3)–(6). Figure 3 shows this process for JASON-3 and HY-2A (the altimeter with the largest σ0 offset, see Online-only Table 1).
A linear regression analysis is then performed between the buoy and altimeter match-up data (U10 values). Although the buoy data are considered “ground truth” for the purposes of the calibration, such data does contain both sampling and calibration errors7. As a consequence, a conventional regression analysis is not appropriate. However, in such cases, a reduced major axis (RMA) regression can be used45. This regression minimizes the triangular area bounded by the vertical and horizontal offsets between the data point and the regression line and the cord of the regression line. This is in contrast to a conventional regression which minimizes the vertical axis offset from the regression line. In addition, standard least squares regression analysis is highly sensitive to outliers. Such outliers can be removed by the use of robust regression46. Robust regression assigns a weight to each point, with values between 0 and 1. Points with a value less than 0.1 were designated as outliers and removed from the analysis before applying the RMA regression analysis.
In the type of regression analysis described above, it is desirable to have as many matchups as possible, as this reduces the confidence limits on the calibration (regression) result. Hence, it is usual to pool data from all buoys over the full duration of the altimeter mission7,17. However, such an “average” calibration will mask any changes in the calibration over time (drift or discontinuities in calibration). Such issues can be addressed by firstly calibrating the individual altimeters against all buoy data (average calibration) and then examining the differences between buoy and altimeter (with average calibration) as a function of time7.
Young et al.7, identified a number of such changes to calibration in their analysis of GEOSAT, ERS-1, TOPEX, ERS-2, GFO and ENVISAT. For the seven additional altimeters included here, discontinuities in the significant wave height of HY-2A and the wind speed of CRYOSAT-2 (see Fig. 4) were identified. Other altimeters do not change their calibration significantly during their respective missions. Note that the present results for HY-2A are consistent with the results of Liu et al.47.
Figure 4 shows the difference between buoy and altimeter values of wind speed, ΔU10 as a function of time for CRYOSAT-2. As can be seen in this figure, a clear change in calibration occurs in mid-2014. When such discontinuities were identified in the data, a piecewise calibration was performed. That is, the altimeter was calibrated separately either side of the discontinuity. Figure 5 shows the result, once the data were calibrated in this fashion, clearly removing the discontinuity.
In Figs 4 and 5 there is a clear periodicity in the data with an annual signal in ΔU10. As demonstrated in Young and Donelan10 this is a result of changes in the structure of the atmospheric boundary layer as a result of changes in the air-water temperature difference (atmospheric stability). These stability effects do not impact Hs and no attempt has been made to correct U10 for this effect.
As noted earlier, SARAL operates in the Ka frequency band, whereas all other altimeters operate in the Ku-band. As a consequence, the parameters in the U10 − σ0 relations (2) and (3) were defined by (5). Examination of scatter and Q − Q plots between buoy and SARAL wind speeds showed good agreement using this approach. However, when cross-validation was carried out with other altimeters (see Technical validation below) and the wind speed range was extended to higher values, it was clear that the SARAL calibration under-estimated higher wind speeds. This behavior is shown in the altimeter-altimeter validation Q − Q plots in Fig. 6.
In order to address this issue, the other calibrated altimeters in orbit at the same time as SARAL (JASON-2, JASON-3, CRYOSAT-2, and SENTINEL-3A) were used to determine a wind speed correction for SARAL wind speed U10 > 10 ms−1. The wind speed correction developed is quadratic (see Online-only Table 1). The available data for the correction was limited to U10 < 24 ms−1. As caution should be exercised in a quadratic extrapolation, wind speeds which are greater than 24 ms−1 have been flagged as “bad”. As a result, the calibration relation for SARAL wind speed has been separated into two regions – U10 < 10 ms−1 and 10 ms−1 ≤ U10 ≤ 24 ms−1. The final calibration relationships for significant wave height are shown in Online-only Table 2 and for wind speed in Online-only Table 1.
Data Records
A total of 26 parameters, as outlined in Table 2 are archived in the repository6. Again, since SARAL is a Ka-band altimeter, rather than Ku-band, the variable names have been changed accordingly. All data are stored in NetCDF files with the records binned into 1° by 1° bins. Within each bin, full data resolution is provided with the recorded latitude, longitude of every 1 Hz measurement recorded. The binned storage provides a convenient mechanism for most users to access data. Data files are not included for areas where there is no data - land or ice areas or bins where the satellite orbit meant there were no overpasses. Individual files are provided for each of the 13 altimeters as summarized in Table 3. Data commences in 1985 and continues to 2018 except for the short break in 1990 and 1991. It should be noted that although data in the nearshore region is provided in the database, it is recommended for applications more than 50 km offshore. Data less than 50 km offshore which passed all other quality control processes are flagged “2” – “probably good data”.
All data files are provided in NetCDF format following the IMOS (Integrated Marine Observing System) data protocols upon which the project is based48,49. The IMOS standard flag system is used for all data flags – where 1, 2, 3, 4, and 9 represent Good_data, Probably_good_data, SAR-mode altimeter data or hardware error (CRYOSAT-2 only), Bad_data and Missing_data, respectively. Note that CRYOSAT-2 operated for some geographic regions in SAR-mode. This data has been flagged as “3” in the database. The calibrations developed for CRYOSAT-2 were not developed for SAR-mode data and hence, this data should be used with caution. The filenames follow the format:
where
-
a.
IMOS: name of the project.
-
b.
SRS-Surface-Waves: representing the present facility.
-
c.
MW: M signifies meteorological related parameters and W signifies wave related parameters.
-
d.
ALTIMETER: name of altimeter (variable).
-
e.
FV02: representing the version of the file.
-
f.
Lat: latitude north or south of the most southern border of the 1° file (variable).
-
g.
Lon: the longitude of the most western border of the 1° file (variable).
-
h.
DM00: first version of delayed mode product.
As the full database consists of approximately 500,000 files (Table 3), it has been stored using the following hierarchy for folders:
\Satellite_Name\20degree_by_20degree_subregion\NetCDF_files (as above)
e.g. \JASON1\020S_280E\IMOS_SRS-Surface-Waves_MW_JASON-1_FV02_016S-282E-DM00.nc.
For both the 20-degree subregion and the 1 deg NetCDF file the latitude, longitude signifies the west most and south most locations for the data region.
The data can be accessed in the number of ways:
-
(a)
Static archive
A static “snapshot” of the data as described in this paper has been archived and allocated the identifier https://doi.org/10.26198/5c77588b32cc1. This is a full copy of all data at the date of submission of this publication.
-
(b)
Dynamic archive – AODN graphical portal
As the intention is to update the data at approximately 6-month intervals, a dynamic archive is maintained at the Australian Ocean Data Network (AODN). The AODN portal can be accessed at: https://portal.aodn.org.au/. The user can access the data graphically from the portal. To find the data, the following navigation is recommended.
-
(i)
Click the “Get Ocean Data Now” button
-
(ii)
Scroll to the keyword search box at the bottom left of the screen. Enter the keywords “altimeter waves”.
-
(iii)
Click on the thumbnail map of the world to the right. The graphical interface which opens allows the user to scroll to any area of the world and define a region to download with the mouse. The specific satellites to download can be specified in the menu to the left.
-
(c)
Dynamic archive – Direct interface
The dynamic archive can also be accessed directly as an Amazon S3 archive. It is recommended that this is done using software such as Cyberduck. Instructions to set up such a server can be found at:
https://help.aodn.org.au/downloading-data-from-servers/amazon-s3-servers/
Once access to the S3 server is gained, the user should navigate to:
IMOS/SRS/Surface-Waves/
The dynamic archive is in the folder: Wave-Wind-Altimetry-DM00
The static archive mentioned above is in the folder:
Wave-Wind-Altimetry-DM00_C-20190228T030000Z
Technical Validation
As noted above, a further set of checks to verify the consistency and stability of various altimeters was conducted in the form of cross validations between altimeter missions. The same criteria as for the buoy matchups have been applied for the cross validations (observations within 50 km and 30 min). Again, RMA regression has been performed for each cross validation. Matchup scatter plots, probability density functions as well as Q – Q plots were analyzed for each combination. This follows the same approach used by Young et al.7.
There are a large number of combinations of satellite matchups across the 13 altimeter missions. Three cases are shown below as examples (JASON-1 − JASON-2, CRYOSAT-2 − SENTINEL-3A, JASON-3 − SARAL). In each case, calibrated data are shown. Figure 7 shows RMA cross-validation, Fig. 8 presents Q − Q plots and Fig. 9 shows altimeter - altimeter differences as a function of time. Note that the gaps in the time series in Fig. 9 occur due to changes in orbit of satellites over time. Such changes mean that for a period of time there will be no cross-over points which meet the match-up criteria required. Data are shown for both Hs and U10. As calibrated data are used, the scatter plots (Fig. 7) and Q − Q plots (Fig. 8) should lie along the diagonal and the altimeter – altimeter differences should be zero.
Cross-validation matchup plots between the altimeters for significant wave height and wind speed. Shown are the 1:1 agreement (dashed diagonal line) and the RMA regression (thick solid line). Contours show the density of matchup data points which has been normalized such that the maximum value is 1.0. Contours are drawn at 0.9, 0.8, 0.7, …, 0.1, 0.05, 0.025, 0.01.
In order to analyse the performance of the cross validations, four different statistical parameters, namely bias (B), root-mean square error (RMSE), Pierson’s correlation coefficient (ρ) and scatter index (SI) were used. These parameters were calculated based on the following relations16 in which M and O stand for model and observation, respectively.
A summary of the statistical parameters is provided in Tables 4 to 7. It should be noted that C-2, HY2, J-1, J-2, J-3, SA, and S-3 are abbreviated forms of CRYOSAT-2, Hai Yang-2A, JASON-1, JASON-2, JASON-3, SARAL and SENTINEL-3A, respectively. Moreover, whilst other statistical parameters are commutative, bias is not. Hence, in order to read the bias in Tables 6 and 7, one has to read it from row to column.
All the statistical parameters shown in Tables 4 to 7 indicate consistent performance between the altimeters. All values of wave height correlation coefficient (Table 4) are close to one. Similarly, RMSE values (Table 4) are small, with all values less than 20 cm. Bias and scatter index (Table 6) are also very small, being less than 12 cm and 0.1, respectively. Similar to the cross-validation for the significant wave height, the cross-validation for wind speed indicates excellent agreement, with the exception of HY-2A (Tables 5 and 7). Although the HY-2A wind speed data are clearly of lower quality than the other altimeters, it is still likely that it will be acceptable for most applications. SENTINEL-3A is a new-generation SAR mode altimeter and operates in this mode at all times. As a result, the radar return is no longer Gaussian, which can introduce biases due to swell and relative track angle to swell direction50. The results in Tables 4 to 7 indicate that this platform produces error statistics comparable to the other platforms averaged over all geographic regions. It is possible, however, that its performance in swell-dominated regions may differ from the other platforms. These potential regional differences have not been explored in the present work. It should be noted that NaN values in the tables indicate that the corresponding cross-validations do not satisfied our matchups criteria. It does not mean, they do not have any matchups.
A number of other studies have used this dataset for global studies. Young and Donelan10 have examined global climatology of U10 and Hs and found the data to be consistent with buoy and model reanalysis results. Takbash et al.42 have used the data to examine global extreme value wind speed and wave height (i.e. 1 in 100 year values). They show that the data produces extreme value estimates consistent with buoy data. That study indicates that although the present calibrations are limited to values of U10 < 24 ms−1 and Hs < 9 m the tails of the respective probability distribution functions remain valid above these limits. Young and Ribal51 have used the data to investigate trends in wind speed and wave height. This is a particularly demanding analysis, as it requires long term stability of the data. The results show that wind speed and wave height trends are consistent in both magnitude and spatial distribution and that the wind speed trends are consistent with radiometer and scatterometer data.
Code Availability
All data are available as NetCDF files. The calibration process described in this paper and the production of the NetCDF files were undertaken using Matlab scripts written for this purpose. This code is available from the corresponding author upon request.
Change history
19 June 2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Young, I. R. Seasonal variability of the global ocean wind and wave climate. International Journal of Climatology 19, 931–950 (1999).
Challenor, P. G., Foale, S. & Webb, D. J. Seasonal changes in the global wave climate measured by the Geosat altimeter. International Journal of Remote Sensing 11, 2205–2213 (1990).
Vinoth, J. & Young, I. R. Global Estimates of Extreme Wind Speed and Wave Height. Journal of Climate 24, 1647–1665 (2011).
Alves, J. H. G. M. & Young, I. R. On estimating extreme wave heights using combined Geosat, Topex/Poseidon and ERS-1 altimeter data. Applied Ocean Research 25, 167–186 (2003).
Young, I. R., Zieger, S. & Babanin, A. V. Global trends in wind speed and wave height. Science 332, 451–455 (2011).
Ribal, A. & Young, I. R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Australian Ocean Data Network, https://doi.org/10.26198/5c77588b32cc1 (2019).
Young, I. R., Sanina, E. & Babanin, A. V. Calibration and Cross Validation of a Global Wind and Wave Database of Altimeter, Radiometer, and Scatterometer Measurements. Journal of Atmospheric and Oceanic Technology 34, 1285–1306 (2017).
Jensen, R. et al. Field Laboratory for Ocean Sea State Investigation and Experimentation: FLOSSIE: Intra-measurement evaluation of 6N wave buoy systems. In 14th Int. Workshop on Wave Hindcasting and Forecasting and Fifth Coastal Hazard Symposium (2015).
Gemmrich, J., Thomas, B. & Bouchard, R. Observational changes and trends in northeast Pacific wave records. Geophysical Research Letters 38, L22601 (2011).
Young, I. R. & Donelan, M. A. On the determination of global ocean wind and wave climate from satellite observations. Remote Sensing of Environment 215, 228–241 (2018).
Large, W. G., Morzel, J. & Crawford, G. B. Accounting for Surface Wave Distortion of the Marine Wind Profile in Low-Level Ocean Storms Wind Measurements. Journal of Physical Oceanography 25, 2959–2971 (1995).
Bender, L. C. III., Guinasso, N. L. Jr., Walpert, J. N. & Howden, S. D. Comparison of Methods for Determining Significant Wave Heights—Applied to a 3-m Discus Buoy during Hurricane Katrina. Journal of Atmospheric and Oceanic Technology 27, 1012–1028 (2010).
Taylor, P. K. & Yelland, M. J. Comments on “On the Effect of Ocean Waves on the Kinetic Energy Balance and Consequences for the Inertial Dissipation Technique”. Journal of Physical Oceanography 31, 2532–2536 (2001).
Zeng, L. & Brown, R. A. Scatterometer Observations at High Wind Speeds. Journal of Applied Meteorology 37, 1412–1420 (1998).
Evans, D., Conrad, C. & Paul, F. Handbook of automated data quality control checks and procedures of the National Data Buoy Center. Document 03-02 (NOAA/National Data Buoy Center Tech., 2003).
Zieger, S., Babanin, A. V., Erick Rogers, W. & Young, I. R. Observation-based source terms in the third-generation wave model WAVEWATCH. Ocean Modelling 96, 2–25 (2015).
Zieger, S., Vinoth, J. & Young, I. R. Joint Calibration of Multiplatform Altimeter Measurements of Wind Speed and Wave Height over the Past 20 Years. Journal of Atmospheric and Oceanic Technology 26, 2549–2564 (2009).
Donelan, M. A. The dependence of the aerodynamic drag coefficient on wave parameters. In Proc. First Int. Conf. on Meteorol. and Air-Sea Interaction of the Coastal Zone. 381–387 (Amer. Meteor. Soc., 1982).
Guan, C. & Xie, L. On the Linear Parameterization of Drag Coefficient over Sea Surface. Journal of Physical Oceanography 34, 2847–2851 (2004).
Zieger, S. Long term trends in ocean wind speed and wave height PhD thesis, 177pp (Swinburne University of Technology, 2010).
Queffeulou, P. & Croizé-Fillon, D. Global altimeter SWH data set - version 11.0. 10pp (IFREMER, Plouzané, France, 2017).
Scharroo, R. et al. RADS: Consistent multi-mission products. In Proc. of the Symposium on 20 Years of Progress in Radar Altimetry ESA SP-710, 66 (Eur. Space Agency Spec. Publ., 2013).
NSOAS. HY-2A satellite user guide. 7pp (National Satellite Ocean Application Service, 2013).
Ash, E., Carter, D. & Collard, F. GlobWave satellite wave data quality report D.16, 69 (Logica UK Ltd, 2010).
Naeije, M., Schrama, E. & Scharroo, R. The Radar Altimeter Database System project RADS. In IGARSS 2000. IEEE 2000 International Geoscience and Remote Sensing Symposium 2, 487–490 (IEEE, 2000).
Young, I. R. & Holland, G. J. Atlas of the Ocean: Wind and Wave Climate. (Pergamon, 1996).
Leys, C., Ley, C., Klein, O., Bernard, P. & Licata, L. Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. Journal of Experimental Social Psychology 49, 764–766 (2013).
Huber, P. J. Robust Statistics. 320pp (Wiley, 2005).
Rousseeuw, P. J. & Croux, C. Alternatives to the median absolute deviation. Journal of the American Statistical association 88, 1273–1283 (1993).
Miller, J. Short Report: Reaction Time Analysis with Outlier Exclusion: Bias Varies with Sample Size. The Quarterly Journal of Experimental Psychology Section A 43, 907–912 (1991).
Quilfen, Y. & Chapron, B. Ocean Surface Wave‐Current Signatures From Satellite Altimeter Measurements. Geophysical Research Letters 46, 253–261 (2019).
Ardhuin, F. et al. Small‐scale open ocean currents have large effects on wind wave heights. Journal of Geophysical Research: Oceans 122, 4500–4517 (2017).
Dobson, E., Monaldo, F., Goldhirsh, J. & Wilkerson, J. Validation of Geosat altimeter-derived wind speeds and significant wave heights using buoy data. Journal of Geophysical Research: Oceans 92, 10719–10731 (1987).
Monaldo, F. Expected differences between buoy and radar altimeter estimates of wind speed and significant wave height and their implications on buoy-altimeter comparisons. Journal of Geophysical Research: Oceans 93, 2285–2302 (1988).
Gower, J. F. R. Intercalibration of wave and wind data from TOPEX/POSEIDON and moored buoys off the west coast of Canada. Journal of Geophysical Research: Oceans 101, 3817–3829 (1996).
Queffeulou, P. Validation of ENVISAT RA-2 and JASON-1 altimeter wind and wave measurements. In IEEE International Geoscience and Remote Sensing Symposium 5, 2987–2989 (2003).
Queffeulou, P. Long-Term Validation of Wave Height Measurements from Altimeters. Marine Geodesy 27, 495–510 (2004).
Queffeulou, P., Bentamy, A. & Guyader, J. Satellite wave height validation over the Mediterranean Sea. In Proceedings of the 2004 Envisat and ERS Symposium, Salzburg, Austria ESA SP-572, 333 (European Space Agency, 2004).
Abdalla, S. Ku-band radar altimeter surface wind speed algorithm. Marine Geodesy 35, 276–298 (2012).
Lillibridge, J., Scharroo, R., Abdalla, S. & Vandemark, D. One- and Two-Dimensional Wind Speed Models for Ka-Band Altimetry. Journal of Atmospheric and Oceanic Technology 31, 630–638 (2014).
Young, I. R. An estimate of the Geosat altimeter wind speed algorithm at high wind speeds. Journal of Geophysical Research: Oceans 98, 20275–20285 (1993).
Takbash, A., Young, I. R. & Breivik, Ø. Global Wind Speed and Wave Height Extremes Derived from Long-Duration Satellite Records. Journal of Climate 32, 109–126 (2019).
Quilfen, Y., Vandemark, D., Chapron, B., Feng, H. & Sienkiewicz, J. Estimating gale to hurricane force winds using the satellite altimeter. Journal of Atmospheric and Oceanic Technology 28, 453–458 (2011).
Gourrion, J. et al. A two-parameter wind speed algorithm for Ku-band altimeters. Journal of Atmospheric and Oceanic technology 19, 2030–2048 (2002).
Smith, R. J. Use and misuse of the reduced major axis for line-fitting. American Journal of Physical Anthropology 140, 476–486 (2009).
Holland, P. W. & Welsch, R. E. Robust regression using iteratively reweighted least-squares. Communications in Statistics - Theory and Methods 6, 813–827 (1977).
Liu, Q. et al. Calibration and Validation of HY-2 Altimeter Wave Height. Journal of Atmospheric and Oceanic Technology 33, 919–936 (2016).
IMOS. IMOS NetCDF Conventions, https://s3-ap-southeast-2.amazonaws.com/content.aodn.org.au/Documents/IMOS/Conventions/IMOS_NetCDF_Conventions.pdf (2015).
IMOS. IMOS NetCDF File Naming Convention, https://s3-ap-southeast-2.amazonaws.com/content.aodn.org.au/Documents/IMOS/Conventions/IMOS_NetCDF_File_Naming_Convention.pdf (2015).
Moreau, T. et al. Impact of long ocean waves on wave height retrieval from SAR altimetry data. Advances in Space Research 62, 1434–1444 (2018).
Young, I. R. & Ribal, A. Multi-platform evaluation of global trends in wind speed and wave height. Science 364, 548–552 (2019).
Acknowledgements
The authors acknowledge ongoing support from the Australian Research Council through grants DP130100215 and DP160100738 and to Integrated Marine Observing System (IMOS) for directly funding the development of this archive. As noted in the paper, the original data were sourced from Globwave, RADS and NSOAS. These repositories are gratefully acknowledged. Any use of the present data must also be acknowledged using the following statement: “Data were sourced from the Integrated Marine Observing System (IMOS) - IMOS is a national collaborative research infrastructure, supported by the Australian Government”.
Author information
Authors and Affiliations
Contributions
I.R.Y. conceived the project and undertook the analysis of the earlier altimeters described in Young et al.7. A.R. performed the analysis of the more recent altimeters, developed the database files and the archiving of the data. Both authors contributed to the writing of the paper.
Corresponding author
Ethics declarations
Competing Interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Online-only Tables
ISA-Tab metadata file
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files associated with this article.
About this article
Cite this article
Ribal, A., Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci Data 6, 77 (2019). https://doi.org/10.1038/s41597-019-0083-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41597-019-0083-9
This article is cited by
-
An 8-model ensemble of CMIP6-derived ocean surface wave climate
Scientific Data (2024)
-
Wind-wave climate changes and their impacts
Nature Reviews Earth & Environment (2024)
-
A dataset of global tropical cyclone wind and surface wave measurements from buoy and satellite platforms
Scientific Data (2024)
-
Assessment of satellite altimetry SWH measurements by in situ observations within 25 km from the coast
Ocean Dynamics (2024)
-
High-resolution calibrated and validated Synthetic Aperture Radar Ocean surface wind data around Australia
Scientific Data (2023)