Abstract
Despite progress in clinical care for patients with coronavirus disease 2019 (COVID-19)1, population-wide interventions are still crucial to manage the pandemic, which has been aggravated by the emergence of new, highly transmissible variants. In this study, we combined the SIDARTHE model2, which predicts the spread of SARS-CoV-2 infections, with a new data-based model that projects new cases onto casualties and healthcare system costs. Based on the Italian case study, we outline several scenarios: mass vaccination campaigns with different paces, different transmission rates due to new variants and different enforced countermeasures, including the alternation of opening and closure phases. Our results demonstrate that non-pharmaceutical interventions (NPIs) have a higher effect on the epidemic evolution than vaccination alone, advocating for the need to keep NPIs in place during the first phase of the vaccination campaign. Our model predicts that, from April 2021 to January 2022, in a scenario with no vaccine rollout and weak NPIs (\({\cal{R}}_0\) = 1.27), as many as 298,000 deaths associated with COVID-19 could occur. However, fast vaccination rollouts could reduce mortality to as few as 51,000 deaths. Implementation of restrictive NPIs (\({\cal{R}}_0\) = 0.9) could reduce COVID-19 deaths to 30,000 without vaccinating the population and to 18,000 with a fast rollout of vaccines. We also show that, if intermittent open–close strategies are adopted, implementing a closing phase first could reduce deaths (from 47,000 to 27,000 with slow vaccine rollout) and healthcare system costs, without substantive aggravation of socioeconomic losses.
Similar content being viewed by others
Main
Since the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) genome was sequenced3, researchers have rushed to develop vaccines to curb the spread of COVID-19 (refs. 4,5). Given the infeasibility of long-term lockdowns6,7 and of effective contact tracing at high case numbers, as well as the availability of several approved COVID-19 vaccines, many countries have invested in mass vaccination rollouts. As of 13 March 2021, four vaccines—Pfizer/BioNTech, Moderna, Oxford–AstraZeneca AZD1222 and J&J Ad26.COV2.S—have been approved by the European Medicines Agency and the Italian Medicines Agency. The reported efficacy rates are 94% and 95%, respectively, for the Moderna and Pfizer/BioNTech vaccines8,9, up to 81.3% for AZD1222 after the second dose with a longer prime–boost interval10 and up to 85% in preventing severe disease for J&J Ad26.COV2.S 28 d after vaccination11. All vaccines have been reported to have favorable safety profiles8,9,11,12,13,14. Italy’s vaccination program started in late December 202015,16 and prioritized healthcare workers, nursing home residents and people over 80 years of age17,18. As of 26 March 2021, 2,787,749 people have been vaccinated in Italy with both doses (8,765,085 doses have been administered in total)19.
Multi-pronged countermeasures, including distancing, testing and tracing, are necessary to achieve a sustained reduction in infection cases20, even more so in light of the recent emergence of new SARS-CoV-2 variants21, such as B.1.1.7 and B.1.351, which are reported to have increased transmissibility22,23 and possibly cause more severe disease24 compared to the original strain. Vaccination alone is not expected to be able to control the spread of the infection, and a carefully planned vaccination campaign25,26 needs to be coordinated with continued implementation of NPIs27 until sufficient coverage is reached to make the case fatality rate (CFR) similar to that of seasonal influenza. Table 1 outlines the main findings and implications for policy of our study.
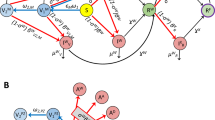
With vaccines and variants as potential game-changers, new models to forecast epidemic scenarios and assess the associated healthcare costs are essential. Our proposed integrated model (Fig. 1a) uses the compartmental model SIDARTHE2 (which we have extended here to include the effects of vaccination and now termed SIDARTHE-V) to provide the predicted evolution of new positive cases; based on new positive cases, a new data-based dynamic model derived from Italian field data computes the time profile of the resulting healthcare system costs, including hospital and intensive care unit (ICU) occupancy and deaths. Although age classes are not explicitly included in our compartmental model, they are accounted for by the data-driven model. To capture the progressive vaccination in reverse age order, the model takes into account age-dependent aggravation and death probability (Extended Data Fig. 5). Details are provided in the Methods.
a, Graphical scheme of our model (adapted from Giordano et al.2). The compartmental SIDARTHE-V epidemiological model provides daily new cases as an input to a novel data-based model of casualties and healthcare system costs. The SIDARTHE-V model captures the dynamic interactions among nine mutually exclusive infection stages in the population: S, Susceptible (uninfected); I, Infected (asymptomatic infected, undetected); D, Diagnosed (asymptomatic infected, detected); A, Ailing (symptomatic infected, undetected); R, Recognized (symptomatic infected, detected); T, Threatened (infected with life-threatening symptoms, detected); H, Healed (recovered); E, Extinct (dead); and V, Vaccinated (successfully immunized). The SIDARTHE-V model provides the time evolution of daily new infection cases, based on which the data-driven model computes the evolution of deaths and ICU and hospital occupancy. b, Death versus vaccination speed curves. For a given \({\cal{R}}_0\) profile, the curve gives the death toll in the period from April 2021 to January 2022 as a function of the average vaccination speed, measured as the fraction of vaccinated population at the end of the period. The death versus vaccination speed curves corresponding to a constant reproduction number are reported in purple (\({\cal{R}}_0 = 1.27\)), orange (\({\cal{R}}_0 = 1.1\)) and blue (\({\cal{R}}_0 = 0.9\)), whereas those corresponding to intermittent strategies are reported in red (Open–Close) and green (Close–Open).
We compare different scenarios to assess the effect of mass vaccination campaigns with different paces, in the presence of varying profiles of the reproduction number \({\cal{R}}_0\) over time, due to specific SARS-CoV-2 variants and/or restrictions. We consider four effective vaccination schedules (Extended Data Fig. 4), obtained by modulating linearly the speed of the four phases, T1–T4, of Italy’s vaccination plan28 and yielding a different fraction of immunized people within January 2022: absent (0%), slow (47%), medium (64%) and fast (90%). We also consider five different time profiles of \({\cal{R}}_0\): constant \({\cal{R}}_0 = 1.27\) (high transmission); Open–Close periodic \({\cal{R}}_0\) with average value of 1.1, in which 1-month Openings (\({\cal{R}}_0 = 1.27\): leaving schools and shops open, wearing face masks and keeping physical distance) alternate with 1-month Closures (\({\cal{R}}_0 = 0.9\): closing schools, shops, restaurants and entertainment places), starting with an Opening phase; constant \({\cal{R}}_0 = 1.1\); Close–Open periodic \({\cal{R}}_0\) with average value of 1.1, in which 1-month Closures alternate with 1-month Openings, starting with a Closure phase; constant \({\cal{R}}_0 = 0.9\) (eradication).
Our main findings are summarized by the deaths versus speed curves in Fig. 1b, which show mortality as a function of the vaccination rollout speed for each \({\cal{R}}_0\) profile. Vaccination is assumed to reduce viral transmission as well as disease severity and risk of death. The different vaccination schedules could also be interpreted as different proportions of infections, diseases and deaths that the vaccine successfully stops, thus constituting a sensitivity analysis. The combination of the four vaccination schedules with the five \({\cal{R}}_0\) profiles leads to 20 distinct scenarios (Fig. 1b). Eradication is associated with an almost constant curve; however, with \({\cal{R}}_0 = 1.27\), the proportion of deaths with slow, medium and fast vaccination schedules could be as small as 30%, 24% and 17% of the 298,000 deaths with no vaccination, respectively. The deaths versus speed curves are flatter when \({\cal{R}}_0\) is kept smaller; implementation of stringent NPIs drastically reduces sensitivity to vaccination delays. Restrictive containment strategies (\({\cal{R}}_0 = 0.9\)) lead to a number of deaths that could be as small as 10% of deaths with weak restrictions (\({\cal{R}}_0 = 1.27\)): depending on the \({\cal{R}}_0\) profile, deaths in the period from April 2021 to January 2022 vary in the range of 30,000–298,000 (no vaccination rollout), 20,000–91,000 (slow vaccination rollout), 19,000–72,000 (medium vaccination rollout) and 18,000–51,000 (fast vaccination rollout). Therefore, NPIs appear to have a stronger effect on mortality than vaccination speed. When planning mid-term interventions, pre-emption reduces mortality and healthcare system costs at no additional socioeconomic cost by comparison with delayed implementation. Both intermittent restrictions with the same average \({\cal{R}}_0\) involve similar socioeconomic costs, but starting with a Closing phase improves on constant containment, which is better than starting with an Opening phase. For all vaccination schedules, the Close–Open strategy saves more than 14,000 lives compared to Open–Close. Hospital and ICU occupancy as a function of the vaccination speed follow a similar pattern (Extended Data Fig. 8).
Considering a medium vaccination speed, Fig. 2a–f shows the epidemic evolution for different constant values of \({\cal{R}}_0\) (the scenarios in the absence of vaccination are in Extended Data Fig. 2). Despite vaccination and implementation of current containment measures, a higher transmissibility due to the spread of new variants would cause a dramatic surge in infection cases, leading, within 2 months, to a peak of almost 4,000 ICU beds needed and more than 700 daily deaths. To prevent this from happening and to reduce hospital occupancy and mortality, \({\cal{R}}_0\) can be reduced through increased stringency of NPIs, particularly in the presence of highly transmissible variants.
Time evolution of the epidemic, in the presence of medium-speed vaccination (64% of the population vaccinated within January 2022), when: a–f, different constant values of \({\cal{R}}_0\), namely \({\cal{R}}_0 = 1.27\) (purple), \({\cal{R}}_0 = 1.1\) (orange) and \({\cal{R}}_0 = 0.9\) (blue), are assumed, resulting from different variants and/or containment strategies, and when: g–l, two alternative intermittent strategies are enforced, with an average value of \({\cal{R}}_0\) equal to 1.1. The Open–Close strategy (red) switches every month between \({\cal{R}}_0 = 1.27\) and \({\cal{R}}_0 = 0.9\) starting with \({\cal{R}}_0 = 1.27\). The Close–Open strategy (green) switches every month between \({\cal{R}}_0 = 0.9\) and \({\cal{R}}_0 = 1.27\) starting with \({\cal{R}}_0 = 0.9\). a,g, Time evolution of the fractions of susceptibles, vaccinated, infected and recovered, and dead. b,h, Daily new cases. c,i, Active cases. d,j, Hospital occupancy. e,k, ICU occupancy. f,l, Daily deaths.
The need to implement new restrictions is likely to trigger intermittent containment measures, with the alternation of higher-\({\cal{R}}_0\) and lower-\({\cal{R}}_0\) phases29,30. In Open–Close strategies, closures are delayed and applied only in anticipation of the pressure on the healthcare system becoming unbearable. Each intermittent Open–Close strategy can be associated with a Close–Open strategy that alternates opening and closing phases of the same duration, with the only difference of starting with a closure. Figure 2g–l compares the two different intermittent strategies, with average \({\cal{R}}_0\) equal to 1.1, under medium-speed vaccination (the scenarios in the absence of vaccination are in Extended Data Fig. 3). Opening first (Open–Close) or closing first (Close–Open) strongly affects healthcare system costs (which depend on case numbers), whereas socioeconomic costs (which depend on the duration and stringency of restrictions) are substantially unchanged. Without aggravation of social and economic losses with respect to an Open–Close strategy, a pre-emptive Close–Open strategy drastically reduces forthcoming infection numbers (decreasing the peak of daily new cases from 38,000 to 14,000), hospital and ICU occupancy and deaths (decreasing the peak of daily deaths from 600 to 400). Even though the average \({\cal{R}}_0\) is above 1, the effective reproduction number \({\cal{R}}_t = {\cal{R}}_0S(t)\) goes below 1 due to the decreasing susceptible fraction S(t); hence, the epidemic is eventually suppressed (Methods).
Finally, we comparatively assess the effect of mass vaccination with different paces (which could be also interpreted as the effect of different vaccine efficacy). We assume that the number of reinfections occurring within the considered horizon is negligible. Figure 3 compares the effect of slow versus fast vaccination under the intermittent Open–Close strategy. Although vaccination leads to a net reduction in deaths and hospital and ICU occupancy compared to the corresponding scenario without vaccination, the difference in effect between slow and fast vaccination is modest. The speed of vaccination becomes more important with a higher \({\cal{R}}_0\), at the price of many more deaths. In Extended Data Figs. 6 and 7, we also consider an adaptive vaccination scenario, where an increase in the number of current infection cases leads to a reduction of the vaccination rate, due to the augmented strain on the healthcare system. Both mortality and healthcare system costs increase, reinforcing conclusions about the greater importance of containment measures over vaccination rates.
Time evolution of the epidemic, with an intermittent Open–Close strategy enforced, in the presence of slow vaccination (47% of the population vaccinated within January 2022, red) or fast vaccination (90% of the population vaccinated within January 2022, blue). a, Time evolution of the fractions of susceptible, vaccinated, infected and recovered, and dead. b, Daily new cases. c, Active cases. d, Hospital occupancy. e, ICU occupancy. f, Daily deaths.
There are limitations to our study. The SIDARTHE-V model is a mean-field compartmental model, which relies on the assumption of a large population with homogeneous mixing and provides predictions that are averaged over the whole population; hence, geographical heterogeneity is not taken into account. More complex and detailed models, which account for spatial effects, social networks and the specificity of individual behaviors, can be developed and used to evaluate vaccination strategies31. Also, we assumed that vaccination is effective against SARS-CoV-2 variants. However, several concerns are raised regarding variants and their potential for vaccine-induced immunity escape32,33; preliminary reports suggest that some COVID-19 vaccines might retain efficacy against variants34,35, although it might be attenuated36, whereas data suggest that Oxford–AstraZeneca AZD1222 might be less effective against B.1.351 (ref. 37). In our scenarios, we also optimistically assumed that successfully vaccinated individuals gain protection against death and hospitalization starting 3 weeks after the first vaccine dose rather than after the second dose.
Vaccination started with slow rates, and priority was given to healthcare personnel, thus delaying the CFR decrease: even under the fast rollout, the CFR would not be halved before June (Extended Data Fig. 4c). Because the decrease rate of the CFR cannot be made arbitrarily fast, due to availability and administration rate of vaccines, our findings confirm that, in the first phase of the mass vaccination campaign, NPIs are crucial, regardless of the (realistic) vaccination speed. Given the circulation of highly transmissible SARS-CoV-2 variants and the risk of potential emergence of vaccine-resistant mutations, \({\cal{R}}_0\) must be kept low until a sufficient level of population immunity is achieved and a large enough portion of the vulnerable population has been immunized. Only then can NPIs be safely and gradually released; the time at which this happens will depend on the speed of vaccine rollout.
To outrun the faster spread of the virus variants, the United Kingdom (UK) launched an extensive COVID-19 vaccination campaign, accelerated by extending the interval between doses: more than 29 million people have received at least one vaccine dose as of 25 March, which has reduced deaths and hospital admissions38. Our model confirms that implementation of strong NPIs could bring the epidemic under control without vaccines or before reaching population immunity, as happened in the UK during January 2021: the highly transmissible B.1.1.7 variant, which first emerged in Kent, UK, and spread throughout the UK, was brought under control by lockdown restrictions kept in place during the first crucial phases of the vaccine rollout campaign. In the meantime, vaccine rollout in the UK has enabled planning subsequent gradual release of NPIs38,39. Although the UK is heading into the second phase of the vaccination campaign, Italy is at an early phase, close to the UK’s first. To contain the new Italian outbreak of SARS-CoV-2, driven by the new variants of concern, it is important to maintain NPIs to prevent an uncontrolled surge in the number of infections, hospitalizations and deaths, because vaccination alone will be insufficient to control the epidemic. In parallel, accelerating the vaccination campaign, as was done in the UK (perhaps also by increasing the interval between doses), would be worth considering.
Methods
Our overall model (Fig. 1a) combines the flexibility and insight of compartmental models with the intrinsic robustness of a black-box healthcare system cost model based on observed data. The SIDARTHE-V model, including the compartment of vaccinated individuals (first block in Fig. 1a), generates the predicted evolution of new positive cases, which is used by the data-based model (second block in Fig. 1a) that captures hospitalization flows and quantifies healthcare system costs in terms of deaths and of hospital and ICU occupancy.
The data used to inform the model are taken from publicly available repositories and reports: https://github.com/pcm-dpc/COVID-19/tree/master/dati-andamento-nazionale for epidemiological data on the evolution of the COVID-19 epidemic in Italy until 12 March 2021; https://www.epicentro.iss.it/coronavirus/bollettino/Bollettino-sorveglianza-integrata-COVID-19_13-gennaio-2021.pdf for age-dependent CFRs; and http://dati.istat.it/Index.aspx for demographic information on the Italian population (needed to take age classes into account). Indeed, although age classes are not explicitly included in our compartmental SIDARTHE-V model, they are taken into account by the data-based model for healthcare system costs, which quantifies hospitalizations, ICU occupancy and deaths. The CFRs (and hospitalization rates) are computed by taking population age classes into account, as shown in Extended Data Fig. 5, using demographic information from http://dati.istat.it/Index.aspx.
SIDARTHE-V compartmental model
The SIDARTHE-V compartmental model shown in Fig. 1a extends the SIDARTHE model, introduced by Giordano et al.2, by including the effect of vaccination. This leads to nine possible stages of infection: susceptible individuals (S) are uninfected and not immunized; infected individuals (I) are asymptomatic and undetected; diagnosed individuals (D) are asymptomatic but detected; ailing individuals (A) are symptomatic but undetected; recognized individuals (R) are symptomatic and detected; threatened individuals (T) have acute life-threatening symptoms and are detected; healed individuals (H) have had the infection and recovered; extinct individuals (E) died because of the infection; and vaccinated individuals (V) have successfully obtained immunity without having been infected.
The dynamic interaction among these nine clusters of the population is described by the following nine ordinary differential equations, describing how the fraction of the population in each cluster evolves over time:
The uppercase Latin letters (state variables) represent the fraction of population in each stage, whereas all the considered parameters, denoted by Greek letters, are positive numbers and have the following meaning:
-
The contagion parameters α, β, γ and δ, respectively, denote the transmission rate (defined as the probability of disease transmission in a single contact multiplied by the average number of contacts per person) due to contacts between a Susceptible individual and an Infected, a Diagnosed, an Ailing or a Recognized individual. These parameters can be modified by social distancing policies (for example, closing schools, remote working and lockdown) as well as physical distancing, adoption of proper hygiene behaviors and use of personal protective equipment. The risk of contagion due to Threatened individuals, treated in proper ICUs, is assumed to be negligible.
-
The diagnosis parameters ε and θ, respectively, denote the probability rate of detection, relative to asymptomatic and symptomatic cases. These parameters, also modifiable, reflect the level of attention on the disease and the number of tests performed over the population: they can be increased by enforcing a massive contact tracing and testing campaign.
-
The symptom onset parameters ζ and η represent the probability rate at which an infected individual, respectively, undetected and detected, develops clinically relevant symptoms. Although disease dependent, they might be partially reduced by improved therapies and acquisition of immunity against the virus.
-
The critical/aggravation parameters μ and v, respectively, denote the rate at which undetected and detected infected symptomatic individuals develop life-threatening symptoms. The parameters can be reduced by means of improved therapies and acquisition of immunity against the virus.
-
The mortality parameters τ1 and τ2, respectively, denote the mortality rate for infected individuals with symptoms (presumably in hospital wards) and with acute symptoms (presumably in ICUs) and can be reduced by means of improved therapies.
-
The healing parameters λ, κ, ξ, ρ and σ denote the rate of recovery for the five classes of infected individuals and can be increased thanks to improved treatments and acquisition of immunity against the virus.
-
The vaccination function φ(S(t)) represents the rate at which susceptible individuals successfully achieve immunity through vaccination (the rate depends on both the actual vaccination rate and the vaccine efficacy); possible choices are the state-dependent φ(S(t)) = φS(t), leading to an exponential decay of the number of susceptible individuals, and φ(S(t)) = φS(t) > 0 as long as S(t) > 0 (φ(S(t) = 0 otherwise), leading to a linear decay. In the latter case, φ(t) can be piecewise constant, as in the vaccination profiles in Extended Data Fig. 4. It is worth stressing that any vaccine (Pfizer/BioNTech, Moderna, Oxford–AstraZeneca, J&J and any other) can be considered within the model as the inducer of immunity, without altering the model validity.
Concerning the duration of immunity, correlates of protection against SARS-CoV-2 infection in humans are not yet established, but the results of a clinical trial with the mRNA-1273 vaccine show that, despite a slight expected decline in titers of binding and neutralizing antibodies, mRNA-1273 has the potential to provide durable humoral immunity: as the natural infection, which produces variable antibody longevity and might induce robust memory B cell responses, also mRNA-1273 vaccine elicited primary CD4 type 1 helper T responses 43 d after the first vaccination, and protection persists after 119 d40. Although it is unclear how long protective effects last beyond the first few months after vaccination, some studies suggest that the elicited neutralizing activity is maintained for up to 8 months after the natural infection with SARS-CoV-2 (refs. 41,42). Reasonably, considering that a similar pattern of responses lasting over time will also emerge after vaccinations, it would be at least unlikely that any potential reinfection would occur over the horizon considered by our scenarios. This is why reinfections have not been explicitly considered in the model, given that we are focused on short-term horizons.
Also, it is worth stressing that we are considering the rate of successful immunization, not of vaccine dose administration (this is why immunity is built up with a slower pace with respect to the expected vaccine roll-out logistics); people who get vaccinated, but for whom the vaccine is not effective, remain susceptible and are, therefore, equally at risk of serious disease and death.
The system is compartmental and has the mass conservation property: as it can be immediately checked, \(\dot S\left( t \right) + \dot I\left( t \right) + \dot D\left( t \right) + \dot A\left( t \right) + \dot R\left( t \right) + \dot T\left( t \right) + \dot H\left( t \right) + \dot E\left( {\mathrm{t}} \right) + \dot V({\mathrm{t}}) = 0\), hence the sum of the states (total population) is constant. Because the variables denote population fractions, we have:
where 1 denotes the total population, including deceased. Note that H(t), E(t) and V(t) are cumulative variables that depend only on the other ones and on their own initial conditions.
Given an initial condition S(0), I(0), D(0), A(0), R(0), T(0), H(0), E(0) and V(0) summing up to 1, if the vaccination function φ(S(t)) > 0 as long as S(t) > 0, the variables converge to
with \(\bar H + \bar E + \bar V = 1\). So only the vaccinated/immunized, the healed and the deceased populations are eventually present, meaning that the epidemic phenomenon is over. All the possible equilibria are given by \(\left( {0,0,0,0,0,0,\bar H,\bar E,\bar V} \right)\), with \(\bar H + \bar E + \bar V = 1\).
To better understand the system behavior, we partition it into three subsystems: the first includes just variable S (corresponding to susceptible individuals); the second, which we denote as the IDART subsystem, includes I, D, A, R and T (the infected individuals); and the third includes variables H, E and V (representing healed, defunct and vaccinated/immunized).
The overall system can be seen as a positive linear system subject to a feedback signal u. Defining x = [I D A R T]T, we can rewrite the IDART subsystem as
where \(r_1 = \varepsilon + \zeta + \lambda\), \(r_2 = {\upeta} + \rho\), \(r_3 = {\uptheta} + {\upmu} + \kappa\), \(r_4 = {\upnu} + \xi + \tau _1\) and \(r_5 = {\upsigma} + \tau _2\). The remaining variables satisfy the differential equations
We can also distinguish between diagnosed healed HD(t), evolving as
and undiagnosed healed HU(t), evolving as
Then, the overall system is described by the infection stage dynamics
along with the equations for S(t), E(t) and H(t) (or, equivalently, HD(t) and HU(t)).
The parametric reproduction number \({\cal{R}}_0\) is the H∞ norm of the positive system from u to ys with parameters tuned at the beginning of the epidemic—that is, when the fraction of susceptible individuals is 1. A simple computation leads to
All the parameters but φ are represented in \({\cal{R}}_0\). Because these parameters depend on the adopted containment measures, on the effectiveness of therapies and of the efficacy of testing and contact tracing, \({\cal{R}}_0\) is time varying in principle. Conversely, the basic reproduction number is the value of the parametric reproduction number at the first onset of the epidemic outbreak, and its value was estimated to range between 2.43 and 3.1 for SARS-CoV-2 in Italy43. The current reproduction number \({\cal{R}}_t\) is the product between \({\cal{R}}_0\) and the susceptible fraction: \({\cal{R}}_t = {\cal{R}}_0S(t)\). Notice that \({\cal{R}}_0\) depends linearly on the contagion parameters. A thorough parameter sensitivity analysis has been worked out for the SIDARTHE model2.
Fundamental mathematical results on the stability and convergence of the model in the absence of vaccination (that is, φ(S(t)) = 0) are summarized next.
The system (10), (14) with constant parameters and constant susceptible population \(S\left( {\bar t} \right)\) is asymptotically stable if and only if \({\cal{R}}_{\bar t} < 1\). The equilibrium point \(\bar x,\bar S\) of system (10), (14) with constant parameters after \(\bar t\) is given by \(\bar x = 0\) and \(\bar S\) satisfying
The condition \({\cal{R}}_t = {\cal{R}}_0S\left( t \right) < 1\) is always verified after a certain time instant, so that \(x\left( t \right) \to 0\) and \(S\left( t \right) \to \bar S\) with \({\cal{R}}_0\bar S < 1\).
As a consequence, epidemic suppression is achieved when the inequality \({\cal{R}}_t = {\cal{R}}_0S\left( t \right) < 1\) is always verified from a certain moment onward.
Fit of the SIDARTHE-V model for the COVID-19 epidemic in Italy
We infer the parameters for models (1)–(9) based on the official data (source: Protezione Civile and Ministero della Salute) about the evolution of the epidemic in Italy from 24 February 2020 through 26 March 2021. We turn the data into fractions over the whole Italian population (~60 million) and adopt a best-fit approach to find the parameters that locally minimize the sum of the squares of the errors.
With parameters estimated based on data until 26 March 2021, the SIDARTHE-V model reproduces the second wave of infection and feeds the health cost model that quantifies the healthcare system costs in different scenarios, encompassing Close–Open strategies during the mass vaccination campaign.
The validation in Extended Data Fig. 1 shows how the SIDARTHE model (initially without vaccination) can faithfully reproduce the epidemic evolution observed so far. In the figures, the evolution over time of the number of active cases, hospitalizations and ICU occupancy, as well as daily deaths, is reported in logarithmic scale, comparing data (dots) with the model prediction (solid line). After 8 March 2020, a strict lockdown brought the Italian effective reproduction number below 1, successfully reversing the COVID-19 epidemic trend. Commercial and recreational activities gradually reopened, until the lockdown was fully lifted on 3 June. The lockdown relaxation coincided with a decreased risk perception and increased social gatherings when, after the first wave, restrictions were eased during the summer. Hence, as expected, a new upward trend in SARS-CoV-2 infections began in mid-August. The increase in daily cases, slow and steady at first, eventually led to a failure in the contact tracing system and the occurrence of a second wave. School reopening in the third week of September led to a steady increase in the number of new cases and hospital and ICU occupancy. This prompted the Italian government, on 4 November, to introduce a three-tier system enforcing diversely strict containment measures on a regional basis, depending on different risk scenarios. The slow decrease of the reproduction and hospitalization numbers led to stricter rules for the period of 24 December to 6 January. The initial onset of the second wave can be promptly identified at the beginning of August 2020, when the infection variables reached a minimum value. The descent phase of the second wave was much slower than that of the first, revealing that the enforced containment measures were milder. In particular, progressive countermeasures were enforced on 24 October (partial limitations), 4 November (regional lockdowns) and December (country-wide lockdown). Mild easing of restrictions and school reopening started on 7 January 2021, whereas other regional measures were implemented on 15 January, subsequently eased and then reinforced.
To reproduce the epidemic evolution over time, the system parameters are piecewise constant and are possibly updated at the following days:
[1 4 12 22 28 36 38 40 47 60 75 119 151 163 182 213 221 253 258 275 276 293 308 320 325 328 342 346 351 368 373 386]
The chosen parameter values are
α = [0.6588 0.4874 0.4886 0.3467 0.2311 0.2543 0.2543 0.3174 0.3467 0.3351 0.3236 0.3236 0.3467 0.4391 0.4045 0.3699 0.4869 0.4166 0.3567 0.3567 0.3267 0.3567 0.3932 0.3533 0.3533 0.4032 0.3034 0.3433 0.4471 0.4471 0.4471 0.3872]
β = [0.012 0.006 0.006 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053 0.0053]
γ = [0.4514 0.2821 0.2821 0.1980 0.1089 0.1089 0.1089 0.1089 0.1089 0.1188 0.1188 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485 0.1485]
δ = [0.0113 0.0056 0.0056 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005]
ε = [0.1703 0.1703 0.1419 0.1419 0.1419 0.1419 0.1992 0.2988 0.2988 0.2988 0.2988 0.6972 0.2490 0.2988 0.2590 0.2294 0.3137 0.2868 0.2868 0.2988 0.2988 0.2988 0.2988 0.3988 0.3988 0.1988 0.2968 0.3088 0.2988 0.2988 0.2988 0.2988]
θ = [0.3705 0.3705 0.3705 0.3705 0.3705 0.3705 0.3705 0.5 0.5 0.5 0.5 0.5 0.5 0.6 0.3 0.6 0.37 0.370 0.37 0.37 0.37 0.37 0.37 0.37 0.37 0.37 0.37 0.37 0.37 0.37 0.37 0.37]
ζ = [0.1254 0.1254 0.1254 0.0340 0.0340 0.0341 0.0250 0.0250 0.0015 0 0.0001 0.0001 0.0005 0.0020 0.0030 0.0020 0.0046 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025 0.0025]
η = [0.1054 0.1054 0.1054 0.0286 0.0286 0.0286 0.0286 0.021 0.0015 0 0 0 0.0005 0.002 0.0031 0.0026 0.003 0.0013 0.0013 0.001 0.0015 0.0018 0.0018 0.0018 0.0018 0.0018 0.0018 0.0018 0.0018 0.0018 0.0018 0.0018]
μ = [0.0205 0.0205 0.0205 0.0096 0.0084 0.0036 0.0036 0.0036 0 0 0 0.0036 0.0036 0 0.0024 0.0036 0.06 0.12 0.12 0. 0.12 0.12 0.12 0.12 0.12 0.12 0.12 0.12 0.12 0.12 0.12 0.12]
ν = [0.03 0.03 0.01 0.01 0.01 0.008 0.007 0.006 0.005 0.004 0.025 0.025 0.0026 0.0026 0.0026 0.002 0.002 0.002 0.002 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02]
τ2 = [0 0 0 0 0 0 0.035 0.045 0.045 0.045 0.4500 0.45 0.02 0 0 0 0 0.0005 0.0005 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17 0.17]
τ1 = [0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.05 0.01 0.01 0 0 0 0 0 0 0.018 0.018 0.001 0.001 0.005 0.001 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005 0.005]
λ = [0.0482 0.0482 0.0482 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128 0.1128]
ρ = [0.0342 0.0342 0.0342 0.017 0.017 0.017 0.02 0.022 0.022 0.045 0.045 0.045 0.02 0.018 0.018 0.018 0.018 0.018 0.032 0.032 0.032 0.032 0.032 0.032 0.032 0.032 0.032 0.032 0.032 0.032 0.032 0.032]
κ = [0.0171 0.0171 0.0171 0.0171 0.0171 0.0171 0.02 0.022 0.022 0.035 0.035 0.035 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02 0.02]
χ = [0.00025 0.00025 0.00025 0.00025 0.00025 0.00025 0.00025 0.0083 0.0083 0.0207 0.012 0.012 0.0037 0.0019 0.0019 0.00067 0.00067 0.00067 0.00015 0.022 0.022 0.032 0.022 0.0220 0.022 0.022 0.0120 0.022 0.012 0.012 0.012 0.012]
σ = [0.0513 0.0513 0.0513 0.0513 0.0513 0.0513 0.03 0.03 0.06 0.075 0.003 0 0 0 0.024 0.024 0.024 0.024 0.0024 0.024 0.024 0.024 0.024 0.024 0.024 0.024 0.024 0.024 0.024 0.024 0.024 0.024]
and lead to the following piecewise constant parametric reproduction number:
\({\cal{R}}_0\) = [2.5200 1.7692 1.9725 1.3859 0.9593 1.0448 0.9162 0.8533 1.0138 0.8997 0.8715 0.5008 1.1494 1.3398 1.3776 1.4154 1.3439 1.2464 1.0104 0.9827 0.9097 0.9812 1.0685 0.9726 0.8150 0.9113 1.0709 0.9516 1.1747 1.2004 1.2651 1.0579]
Starting with day 405 (5 April 2021), the parameters are differentiated depending on the different scenarios associated with the presence of new virus variants and/or of the adoption of different restrictions:
-
High transmission: α = 0.477, leading to a constant \({\cal{R}}_0 = 1.27\)
-
Open–Close: α switches every month between the high value 0.477 and the low value 0.3198; hence, every month \({\cal{R}}_0\) switches between the values 1.27 and 0.9, with an average value of about 1.1.
-
Constant α = 0.4092, leading to \({\cal{R}}_0 = 1.1\)
-
Close–Open: α switches every month between the low value 0.3198 and the high value 0.477; hence, every month \({\cal{R}}_0\) switches between the values 0.9 and 1.27, with an average value of about 1.1. The Close–Open strategy features the same pattern as the Open–Close strategy, the only difference being that it starts with a closure phase.
-
Eradication: α = 0.3198, leading to a constant \({\cal{R}}_0 = 0.9\).
Different parameter choices for the SIDARTHE-V model might yield the same \({\cal{R}}_0\). However, we have fitted our model based on a long history of data (since February 2020) and on a priori information about the epidemic and its management; to show the effect of a different \({\cal{R}}_0\), we are only modifying the infection parameters—that is, the high-sensitivity parameters (according to the thorough sensitivity analysis performed in our previous work2) that are affected by the spread of more transmissible variants and by NPIs. If two different combinations of parameters could fit equally well all the past data history and yield the same \({\cal{R}}_0\), the resulting long-term future evolution would also be similar. Any parameter choice that successfully reproduces the observed total number of cases is suitable for our goal: through the SIDARTHE-V model, we are computing only the predicted total number of detected infection cases, which is then projected onto healthcare system costs (including deaths and hospitalizations) by the data-based model.
The vaccination function is chosen according to the three different profiles shown in Extended Data Fig. 4, where \(\varphi \left( {S\left( t \right)} \right) = \varphi \left( t \right)\) is piecewise constant (of course, \(\varphi \left( {S\left( t \right)} \right) = 0\) when S(t) = 0).
In the adaptive vaccination scenarios in Extended Data Figs. 6 and 7, conversely, the vaccination function is chosen as \({\mathrm{max}}\{ \left[ {1 - r\left( {D\left( t \right) + R\left( t \right) + T\left( t \right)} \right)} \right]\varphi \left( t \right);0\}\), where φ(t) is the same piecewise constant vaccination profile as above, whereas the parameter r is chosen as r = 10−6.
Note that our model accounts for the effective immunization rate, regardless of the adopted vaccine. Any vaccine can be included in the model without altering its validity: the resulting immunization curves can be derived with the same procedure, regardless of the specific vaccine that has been used to achieve immunity.
Adaptive vaccination under a medium vaccination schedule (Extended Data Figs. 6 and 7) leads to increased healthcare system costs with respect to piecewise constant vaccination functions (Figs. 2 and 3) for all \({\cal{R}}_0\) profiles. These costs can be compared with the even worse outcomes that are expected without vaccination, displayed in Extended Data Figs. 2 and 3. When \({\cal{R}}_0 = 1.27\), thousand deaths in the period from April 2021 to January 2022 increase from 90 to 229 (slow speed), from 72 to 220 (medium speed) and from 51 to 204 (fast speed), whereas they would be 298 without vaccination. Under the Open–Close strategy with average \({\cal{R}}_0\) equal to 1.1, thousand deaths in the period from April 2021 to January 2022 increase from 47 to 76 (slow speed), from 42 to 70 (medium speed) and from 35 to 62 (fast speed), whereas they would be 126 without vaccination. When \({\cal{R}}_0 = 1.1\), thousand deaths in the period from April 2021 to January 2022 increase from 34 to 48 (slow speed), from 30 to 44 (medium speed) and from 25 to 38 (fast speed), whereas they would be 96 without vaccination. Under the Close–Open strategy with average \({\cal{R}}_0\) equal to 1.1, thousand deaths in the period from April 2021 to January 2022 increase from 27 to 37 (slow speed), from 24 to 33 (medium speed) and from 21 to 28 (fast speed), whereas they would be 84 without vaccination.
Data-driven model of healthcare system costs
To predict the evolution of deaths from the time series of reported cases, a field estimate of the apparent CFR is needed. This parameter is affected by the testing protocol, the healthcare system reaction and the age distribution of vaccinated people. For these reasons, a specific model should be derived for each country resorting to a data-based approach. We considered the Italian case, but the methodology has general validity and could be promptly applied to other countries. The input–output model predicting deaths from the new cases was derived in two steps. First, a data-based dynamic model for the unvaccinated population was estimated from data collected during the second wave. The static gain of this dynamic model coincides with the CFR for the unvaccinated population. In the second step, this gain was multiplied by a time-varying function that accounts for the lethality decrease consequent to progressive vaccination of older people.
The input of the dynamic model is the time series of new cases n(t), and the output is the time series of daily deaths d(t). Given the variations of testing protocols and the large number of unreported cases during the first wave, the model was estimated using second-wave data collected within a 110-d window ending on 7 February 2021. More recent data were not used because the base CFR model should not be affected by vaccinations, whose effect is suitably incorporated in a second step as detailed below. The model assumes that the deaths at day t depend on the past new cases according to the equation
where the weight w(i) denotes the fraction of individuals who became infected at day t-i who eventually die at day t. The CFR for the unvaccinated population is then given by
To estimate the weights, an exponential model with delay was assumed:
where k is the delay and f and b are unknown parameters. Because both the new cases and the daily deaths exhibit an apparent weekly seasonality, the original series were replaced by their 7-d moving average. Parameters were estimated via least squares using the function oe.m of the MATLAB System Identification Toolbox44. The estimation of f and b was repeated for all delays k ranging from 0 to 15, and the delay k = 3, associated with the best sum of squares, was eventually selected. The estimated parameters and their percent coefficients of variation were:
Then, recalling the formula for the sum of the harmonic series, the second-wave CFR for the unvaccinated population is given by
In the second step, the effect of vaccination on lethality was modeled by estimating a time-varying CFR(t) that depends on the vaccination schedule, described by the fraction V(t) of vaccine-immunized individuals at time t. Order of vaccination follows the reverse of the age. Slower or faster vaccination speeds correspond to different curves V(t), whose rate of increase might be less or more rapid. Three schedules were considered: fast, medium and slow. The fast schedule assumes that each the four phases, T1–T4, of the Italian vaccination plan45 is completed in one trimester. In the medium and slow schedule, the time was linearly extended by a factor 1.2 and 1.4, respectively. The three schedules are graphically displayed in Extended Data Fig. 4. To account for vaccines that were already administered, the scheduled vaccination rate from 27 December 2020 to 12 March 2021 was replaced by the actual average rate of second-dose vaccinations from 27 December to 19 February, considering that immunization develops with some weeks of delay after the administration.
The COVID-19 lethality CFRa for an individual of age a was obtained by rescaling values published the Italian National Institute of Health46. Rescaling was necessary because the published values were inflated by the inclusion of patients who died during the first wave, when new cases were massively underreported. Rescaling was performed in such a way that the overall lethality coincides with CFR0 = 0.027. The profile CFRa is displayed in Extended Data Fig. 5c.
If we assume that the number of deaths does not significantly affect the overall age distribution, the probability P(Age = a) can be directly inferred by ISTAT statistical tables47. The distribution was corrected by subtracting individuals who were already vaccinated on 19 February 2021, whose ages are made available on the vaccine open data repository48. The distribution of population by age is displayed in Extended Data Fig. 5c.
Recalling that V(t) is the fraction of vaccine-immunized individuals, and vaccination order follows the reverse of the age, the probability of death for an individual of age a who becomes infected at time t is
Then, the time-varying CFR is obtained by the total probability theorem:
where \(P(Age = a|Infected,t)\) denotes the probability that the age of an individual is a, knowing that the individual became infected at time t. During the second wave, the age distribution of the infected individuals46 was similar to the age distribution of the Italian population. For instance, 56% of the population is in the age range 0–50 years, 28% is in the range 51–70 years and 16% is older than 70 years. In comparison, 55.6% of diagnosed cases between 18 December 2020 and 10 January 2021 were in age range 0–50 years, 28% in the range 51–70 years and 16.4% over 70 years. Therefore, \(P(Age = a|Infected,t) = P(Age = a)\), so that the CFR of an individual infected at time t can be computed as
The steps of the procedure for the computation of CFR(t) are summarized in Extended Data Fig. 5. The time-varying profiles CFR(t) for the three vaccination schedules are plotted in Extended Data Fig. 4. Because protection against hospitalization and death has been observed already after the first dose, the calculation of the time-varying CFR was based on first dose administration, assumed twice as fast as second dose administration.
Finally, the input–output model that accounts for the effect of vaccination is given by
Due to the time-varying coefficient C(t), the same number of new cases will yield fewer and fewer deaths as vaccination comes to protect older segments of the population.
Dynamic models for hospital and ICU occupancies were developed in a similar way. The estimated parameters and their percent coefficients of variation for hospital occupancy (estimated delay k = 0) were:
Those for ICU occupancy (estimated delay k = 0) were:
Assuming that gravity reduction parallels the lethality one, the effect of vaccination on hospital and ICU occupancies was described by modulating the input through the time-varying coefficient C(t).
As seen in Extended Data Fig. 9, the three data-based dynamic models provide a very good fitting of deaths and hospital and ICU occupancies.
Our scenarios: different values of \({\mathbf{{\cal{R}}}}_0\)
The chosen values of \({\cal{R}}_0\) are based on plausible scenarios, in view of what has been observed throughout the past year in Italy, with a suitable combination of (1) presence of SARS-CoV-2 variants with increased transmissibility and (2) enforced restrictions. In particular, the mild restrictions that kept \({\cal{R}}_0\) around 0.9 with the original virus strain would keep it around 1.3 (at least) if the new variants increase transmissibility of at least 40–50%, as reported in the literature49,50,51. In fact, values around \({\cal{R}}_0\) = 1.3 were observed in mid-March 2021 in areas of Italy where the UK variant is becoming dominant. We have not considered even worse scenarios, because a higher \({\cal{R}}_0\) is unlikely to be sustainable: even stricter restrictions would then be enforced to prevent it from increasing. On the other hand, we deem it unlikely that restrictions so stringent to bring \({\cal{R}}_0\) below 0.9 would be enforced; hence, we have chosen this value as the other extreme scenario.
Our scenarios: intermittent strategies, Open–Close and Close–Open
In some of our scenarios, we consider intermittent strategies that rely on the alternation of Open phases (associated with a larger \({\cal{R}}_0\)) and Close phases (associated with a smaller \({\cal{R}}_0\)) with a fixed proportion.
One of our main results is that, when planning over a fixed time period and having to set the order of two phases (Open and Close) with fixed length, starting with the Close phase is always an advantage. This happens because the associated healthcare system costs depend on the total number of infection cases in the considered time period, which is much larger if the Open phase comes first; hence, starting with a Close phase drastically reduces health costs and losses. On the other hand, socioeconomic costs are proportional to the duration and stringency of the restrictions, regardless of when they are enforced; hence, intermittent closures yield similar socioeconomic costs. Given a finite horizon and Close/Open phases of fixed length, closing before opening does not bring any additional socioeconomic cost, with respect to opening before closing, because the closing (and opening) phases have the same duration in both scenarios.
This principle holds true irrespective of the initial size of the epidemic. For instance, with very low case numbers, starting with a Close phase could approach or even achieve eradication, after which reopening would be completely safe (such an eradication approach has been successfully adopted, for example, by New Zealand52,53), whereas, if starting with an Open phase, the number of infection cases would grow exponentially, and the following Close phase could only mitigate the epidemic expansion. Of course, the higher the initial case number, the more visible the difference between the two strategies.
Also, the principle (if Open and Close phases with a fixed proportion need to be alternated in a periodic fashion, then starting with a Close phase is always preferable) remains valid regardless of the phase duration. In our scenarios, we have chosen 1-month-long phases, because this is a frequently observed choice in many countries (for example, in accordance with implemented policies in Italy but also in Israel) and is a sufficiently long time for the effect of interventions to be well visible.
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
We gathered all epidemiological and demographic data from publicly available sources: https://github.com/pcm-dpc/COVID-19/tree/master/dati-andamento-nazionale, https://www.epicentro.iss.it/coronavirus/bollettino/Bollettino-sorveglianza-integrata-COVID-19_13-gennaio-2021.pdf and http://dati.istat.it/Index.aspx. Data are also included in Extended Data Figs. 1 and 9 and in the code folder: https://giuliagiordano.dii.unitn.it/docs/papers/VaccineVariantsCode.zip.
Code availability
The codes are available at https://giuliagiordano.dii.unitn.it/docs/papers/VaccineVariantsCode.zip.
References
Stasi, C., Fallani, S., Voller, F. & Silvestri, C. Treatment for COVID-19: an overview. Eur. J. Pharmacol. 889, 173644 (2020).
Giordano, G. et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 26, 855–860 (2020).
Wu, F. et al. A new coronavirus associated with human respiratory disease in China. Nature 579, 265–269 (2020).
Wang, J., Peng, Y., Xu, H., Cui, Z. & Williams, R. O. The COVID-19 vaccine race: challenges and opportunities in vaccine formulation. AAPS PharmSciTech. 21, 225 (2020).
Rawat, K., Kumari, P. & Saha, L. COVID-19 vaccine: a recent update in pipeline vaccines, their design and development strategies. Eur. J. Pharmacol. 892, 173751 (2021).
Abbasi, K. Behavioural fatigue: a flawed idea central to a flawed pandemic response. BMJ 370, m3093 (2020).
Rypdal, K., Bianchi, F. M. & Rypdal, M. Intervention fatigue is the primary cause of strong secondary waves in the COVID-19 pandemic. Int. J. Environ. Res. Public Health 17, 9592 (2020).
Polack, F. P. et al. Safety and efficacy of the BNT162b2 mRNA Covid-19 vaccine. N. Engl. J. Med. 383, 2603–2615 (2020).
Baden, L. R. et al. Efficacy and safety of the mRNA-1273 SARS-CoV-2 Vaccine. N. Engl. J. Med. 384, 403–416 (2021).
Voysey, M. et al. Single-dose administration and the influence of the timing of the booster dose on immunogenicity and efficacy of ChAdOx1 nCoV-19 (AZD1222) vaccine: a pooled analysis of four randomised trials. Lancet 397, 881–891 (2021).
US Food and Drug Administration. FDA Briefing Document. Janssen Ad26.COV2.S Vaccine for the Prevention of COVID-19. Vaccines and Related Biological Products Advisory Committee Meeting, February 26, 2021. https://www.fda.gov/media/146217/download
Gee, J. et al. First month of COVID-19 vaccine safety monitoring—United States, December 14, 2020–January 13, 2021. MMWR Morb. Mortal. Wkly Rep. 70, 283–288 (2021).
Voysey, M. et al. Safety and efficacy of the ChAdOx1 nCoV-19 vaccine (AZD1222) against SARS-CoV-2: an interim analysis of four randomised controlled trials in Brazil, South Africa, and the UK. Lancet 397, 99–111 (2021).
European Medicines Agency. COVID-19 Vaccine AstraZeneca: benefits still outweigh the risks despite possible link to rare blood clots with low blood platelets. https://www.ema.europa.eu/en/news/covid-19-vaccine-astrazeneca-benefits-still-outweigh-risks-despite-possible-link-rare-blood-clots (2021).
ANSA. Pfizer vaccine arrives in Italy. https://www.ansa.it/english/news/2020/12/30/pfizer-vaccine-arrives-in-italy_4690fcec-88a8-4919-b821-afc01fc3955a.html (2020).
ANSA. First Moderna vaccine doses arrive in Italy. https://www.ansa.it/english/news/general_news/2021/01/12/first-moderna-vaccine-doses-arrive-in-italy_ce39273f-aa51-4d55-9f8b-d5c658633007.html (2021).
Reuters. Italy kicks off vaccinations against COVID-19 in Rome. https://www.reuters.com/article/health-coronavirus-italy-vaccine/italy-kicks-off-vaccinations-against-covid-19-in-rome-idUKL1N2J703O (2020).
Ministero della salute (Italian Ministry of Health). Vaccinazione anti-SARS-CoV-2/COVID-19: PIANO STRATEGICO: Elementi di preparazione e di implementazione della strategia vaccinale. https://www.vaccinarsinsardegna.org/assets/uploads/files/378/piano-strategico-vaccinazione-anti-covid19.pdf (2020).
Presidenza del Consiglio dei Ministri. Ministero della Salute. Commissario Straordinario Covid-19. Report Vaccini Anti COVID-19. https://www.governo.it/it/cscovid19/report-vaccini/ (2021).
Priesemann, V. et al. Calling for pan-European commitment for rapid and sustained reduction in SARS-CoV-2 infections. Lancet 397, 92–93 (2021).
Priesemann, V. et al. An action plan for pan-European defence against new SARS-CoV-2 variants. Lancet 397, 469–470 (2021).
Davies, N. G. et al. Estimated transmissibility and impact of SARS-CoV-2 lineage B.1.1.7 in England. Science 372, eabg3055 (2021).
Abbott, S., Funk, S. & CMMID COVID-19 Working Group. Local area reproduction numbers and S-gene target failure. https://cmmid.github.io/topics/covid19/local-r-sgtf.html (2021).
Horby, P. et al. NERVTAG note on B.1.1.7 severity. https://www.gov.uk/government/publications/nervtag-paper-on-covid-19-variant-of-concern-b117 (2021).
Bubar, K. M. et al. Model-informed COVID-19 vaccine prioritization strategies by age and serostatus. Science 371, 916–921 (2021).
Ramos A. M., Vela-Pérez, M., Ferrández, M. R., Kubik, A. B. & Ivorra, B. Modeling the impact of SARS-CoV-2 variants and vaccines on the spread of COVID-19. Preprint at ResearchGate https://doi.org/10.13140/RG.2.2.32580.24967/2 (2021).
Grundel, S. et al. How to coordinate vaccination and social distancing to mitigate SARS-CoV-2 outbreaks. Preprint at medRxiv https://doi.org/10.1101/2020.12.22.20248707 (2020).
Ministero della Salute. Vaccinazione anti-SARS-CoV-2/COVID-19, Piano Strategico, elementi di preparazione e di implementazione della strategia vaccinale. http://www.salute.gov.it/imgs/C_17_pubblicazioni_2986_allegato.pdf (2020).
Kissler, S. M. et al. Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 368, 860–868 (2020).
Bin, M. et al. Post-lockdown abatement of COVID-19 by fast periodic switching. PLoS Comput. Biol. 17, e1008604 (2021).
Tetteh, J. N. A., Nguyen, V. K. & Hernandez-Vargas, E. A. COVID-19 network model to evaluate vaccine strategies towards herd immunity. Preprint at medRxiv https://doi.org/10.1101/2020.12.22.20248693 (2020).
Starr, T. N. et al. Prospective mapping of viral mutations that escape antibodies used to treat COVID-19. Science 371, 850–854 (2021).
Fontanet, A. et al. SARS-CoV-2 variants and ending the COVID-19 pandemic. Lancet 397, 952–954 (2021).
Callaway, E. Could new COVID variants undermine vaccines? Labs scramble to find out. Nature 589, 177–178 (2021).
Burki, T. Understanding variants of SARS-CoV-2. Lancet 397, 462 (2021).
Lauring, A. S. & Hodcroft, E. B. Genetic variants of SARS-CoV-2—what do they mean? JAMA 325, 529–531 (2021).
Madhi, S. A. et al. Efficacy of the ChAdOx1 nCoV-19 Covid-19 vaccine against the B.1.351 variant. N. Engl. J. Med. https://doi.org/10.1056/NEJMoa2102214 (2021).
Lopez Bernal, J. et al. Early effectiveness of COVID-19 vaccination with BNT162b2 mRNA vaccine and ChAdOx1 adenovirus vector vaccine on symptomatic disease, hospitalisations and mortality in older adults in England. Preprint at medRxiv https://doi.org/10.1101/2021.03.01.21252652 (2021).
GOV.UK. Coronavirus (COVID‑19). https://www.gov.uk/coronavirus
Widge, A. T. et al. Durability of responses after SARS-CoV-2 mRNA-1273 vaccination. N. Engl. J. Med. 384, 80–82 (2021).
Robbiani, D. F. et al. Convergent antibody responses to SARS-CoV-2 in convalescent individuals. Nature 584, 437–442 (2020).
Dan, J. M. et al. Immunological memory to SARS-CoV-2 assessed for up to 8 months after infection. Science 371, eabf4063 (2021).
D’Arienzo, M. & Coniglio, A. Assessment of the SARS-CoV-2 basic reproduction number, R0, based on the early phase of COVID-19 outbreak in Italy. Biosaf. Health 2, 57–59 (2020).
MATLAB System Identification Toolbox, 9.13 (R2020b). https://www.mathworks.com/products/sysid.html
Italian Ministry of Health. Vaccinazione anti-SARS-CoV-2/COVID-19 PIANO STRATEGICO. https://www.trovanorme.salute.gov.it/norme/renderNormsanPdf?anno=2021&codLeg=78657&parte=1%20&serie=null
Task Force COVID-19 del Dipartimento Malattie Infettive e Servizio di Informatica. Istituto Superiore di Sanità. Epidemia COVID-19: Aggiornamento nazionale. https://www.epicentro.iss.it/coronavirus/bollettino/Bollettino-sorveglianza-integrata-COVID-19_13-gennaio-2021.pdf (2021).
ISTAT-Istituto Nazionale di Statistica. http://dati.istat.it/Index.aspx
GitHub. Covid-19 Opendata Vaccines. https://github.com/italia/covid19-opendata-vaccini
Voltz, E. et al. Transmission of SARS-CoV-2 Lineage B.1.1.7 in England: insights from linking epidemiological and genetic data. Preprint at medRxiv https://doi.org/10.1101/2020.12.30.20249034 (2021).
Moore, J. P. Approaches for optimal use of different COVID-19 vaccines. Issues of viral variants and vaccine efficacy. JAMA https://doi.org/10.1001/jama.2021.3465 (2021).
Davies, N. G. et al. Estimated transmissibility and impact of SARS-CoV-2 lineage B.1.1.7 in England. Science https://doi.org/10.1126/science.abg3055 (2021).
Cousins, S. New Zealand eliminates COVID-19. Lancet 395, 1474 (2020).
Fouda, A., Mahmoudi, N., Moy, N. & Paolucci, F. The COVID-19 pandemic in Greece, Iceland, New Zealand, and Singapore: health policies and lessons learned. Health Policy Technol. 9, 510–524 (2020).
Acknowledgements
We acknowledge financial support through the Italian grant PRIN 2017 ‘Monitoring and Control Underpinning the Energy-Aware Factory of the Future: Novel Methodologies and Industrial Validation’ (ID 2017YKXYXJ). This research has also received funding from the European Union’s Horizon 2020 Research and Innovation Program ‘PERISCOPE: Pan European Response to the ImpactS of COvid-19 and future Pandemics and Epidemics’ under grant agreement no. 101016233, H2020-SC1-PHE-CORONAVIRUS-2020-2-RTD.
Author information
Authors and Affiliations
Contributions
F.B., P.B., P.C., G.D.N. and G.G. proposed the model and performed the model fitting, simulations, analysis and interpretation of the results. R.B., M.C., A.D.F. and P.S. provided first-hand clinical insight and contextualization. All authors wrote and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Medicine thanks Tim Colbourn and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Jennifer Sargent was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Epidemic evolution in Italy from late February 2020 to March 2021.
Data (stars) and estimation (solid lines), based on the SIDARTHE model, of the time evolution of the epidemic, in logarithmic scale. Active cases (current diagnosed infected, related to the SIDARTHE variables R+T+D) are shown in orange; hospital occupancy (related to the SIDARTHE variables R+T) is shown in blue; ICU occupancy (related to variable T) is shown in magenta; daily deaths (related to the derivative of variable E) are shown in black.
Extended Data Fig. 2 Epidemic evolution without vaccination for different constant values of \({\cal{R}}_0\).
Time evolution of the epidemic, in the absence of vaccination, when different constant values of \({\cal{R}}_0\), namely \({\cal{R}}_0 = 1.27\) (purple), \({\cal{R}}_0 = 1.1\) (orange), \({\cal{R}}_0 = 0.9\) (blue), are assumed, resulting from different variants and/or containment strategies. a, Time evolution of the fractions of susceptibles, infected and recovered, and dead. b, Daily new cases. c, Active cases. d, Hospital occupancy. e, ICU occupancy. f, Daily deaths.
Extended Data Fig. 3 Epidemic evolution without vaccination for different intermittent strategies.
Time evolution of the epidemic, in the absence of vaccination, when two alternative intermittent strategies are enforced, with an average value of \({\cal{R}}_0\) equal to 1.1. The Open-Close strategy (red) switches every month between \({\cal{R}}_0 = 1.27\) and \({\cal{R}}_0 = 0.9\), starting with \({\cal{R}}_0 = 1.27\). The Close-Open strategy (green) does the same, but starts with \({\cal{R}}_0 = 0.9\). a, Time evolution of the fractions of susceptibles, infected and recovered, and dead. b, Daily new cases. c, Active cases. d, Hospital occupancy. e, ICU occupancy. f, Daily deaths.
Extended Data Fig. 4 Effective vaccination schedules.
Profiles of the considered three different effective vaccination schedules: slow, medium and fast. For each of the three schedules, we show: the evolution over time of the daily effective vaccination rate, namely the fraction of population successfully immunised (second dose) in one day (a-d-g), the cumulative fraction of immunised population as a function of time (b-e-h), the resulting time-varying Case Fatality Rate as a function of time, obtained taking population age classes into account and assuming a vaccination schedule that prioritises the elderly (c-f-i).
Extended Data Fig. 5 Time-varying age-dependent Case Fatality Rate as a function of the vaccination schedule.
Computation of the time-varying Case Fatality Rate as a function of the vaccination roadmap, taking population age classes into account. a, Considered vaccination roadmap: fraction of non-vaccinated population over time. b, Cumulative Italian population as a function of age. c, Fraction of the population (red) and Case Fatality Rate (purple) as a function of age. d, Evolution of the overall Case Fatality Rate over time, assuming a vaccination schedule that gives priority to the elderly.
Extended Data Fig. 6 Epidemic evolution with adaptive vaccination for different constant values of \({\cal{R}}_0\).
Time evolution of the epidemic, with adaptive vaccination, when different constant values of \({\cal{R}}_0\), namely \({\cal{R}}_0 = 1.27\) (purple), \({\cal{R}}_0 = 1.1\) (orange), \({\cal{R}}_0 = 0.9\) (blue), are assumed, associated with different variants and/or containment strategies. The adaptive vaccination speed is inversely proportional to the size of the epidemic, that is to the number of infection cases. a, Time evolution of the fractions of susceptibles, vaccinated, infected and recovered, and dead. b, Daily new cases. c, Active cases. d, Hospital occupancy. e, ICU occupancy. f, Daily deaths.
Extended Data Fig. 7 Epidemic evolution with adaptive vaccination for different intermittent strategies.
Time evolution of the epidemic, with adaptive vaccination, when different intermittent strategies are enforced, with an average value of \({\cal{R}}_0\) equal to 1.1. The Open-Close strategy (red) switches every month between \({\cal{R}}_0 = 1.27\) and \({\cal{R}}_0 = 0.9\), starting with \({\cal{R}}_0 = 1.27\). The Close-Open strategy (green) does the same, but starts with \({\cal{R}}_0 = 0.9\). The adaptive vaccination speed is inversely proportional to the size of the epidemic, that is to the number of infection cases. a, Time evolution of the fractions of susceptibles, vaccinated, infected and recovered, and dead. b, Daily new cases. c, Active cases. d, Hospital occupancy. e, ICU occupancy. f, Daily deaths.
Extended Data Fig. 8 Health costs as a function of vaccination speed.
Health-cost vs. vaccination-speed curves: for a given \({\cal{R}}_0\) profile, the curve gives the total ICU occupancy (a) and the total hospital occupancy (b) in the period from April 2021 to January 2022, as a function of the average vaccination speed, measured as the fraction of two-dose vaccinated population at the end of the period. The health-cost vs. vaccination-speed curves corresponding to a constant reproduction number are reported in purple (\({\cal{R}}_0 = 1.27\)), orange (\({\cal{R}}_0 = 1.1\)) and blue (\({\cal{R}}_0 = 0.9\)), while those corresponding to intermittent strategies are reported in red (Open-Close) and green (Close-Open).
Extended Data Fig. 9 Dynamic input-output models for health costs.
Estimation of the three dynamic input-output models linking new cases (input) to three outputs: deaths (a), hospital occupancy (b) and ICU occupancy (c). Each panel displays the observed outputs (grey) and the values predicted by the identified dynamic system (blue). In order to allow for weekly oscillations both input and output series were prefiltered with a 7-day moving average before performing nonlinear least squares fitting of a first-order model with delay. The FIT ratios of the three models are 83.16%, 84.67%, and 87.53%.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Giordano, G., Colaneri, M., Di Filippo, A. et al. Modeling vaccination rollouts, SARS-CoV-2 variants and the requirement for non-pharmaceutical interventions in Italy. Nat Med 27, 993–998 (2021). https://doi.org/10.1038/s41591-021-01334-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41591-021-01334-5
This article is cited by
-
Validity of Markovian modeling for transient memory-dependent epidemic dynamics
Communications Physics (2024)
-
Comparing frequency of booster vaccination to prevent severe COVID-19 by risk group in the United States
Nature Communications (2024)
-
A hybrid compartmental model with a case study of COVID-19 in Great Britain and Israel
Journal of Mathematics in Industry (2023)
-
A comparative analysis of the effects of containment policies on the epidemiological manifestation of the COVID-19 pandemic across nine European countries
Scientific Reports (2023)
-
Cost-effectiveness analysis of COVID-19 variants effects in an age-structured model
Scientific Reports (2023)