Abstract
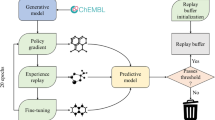
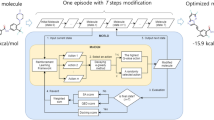
We have developed a deep generative model, generative tensorial reinforcement learning (GENTRL), for de novo small-molecule design. GENTRL optimizes synthetic feasibility, novelty, and biological activity. We used GENTRL to discover potent inhibitors of discoidin domain receptor 1 (DDR1), a kinase target implicated in fibrosis and other diseases, in 21 days. Four compounds were active in biochemical assays, and two were validated in cell-based assays. One lead candidate was tested and demonstrated favorable pharmacokinetics in mice.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
Data availability
All data are available in the main text or the supplementary materials.
Code availability
The code for the GENTRL model is available at http://github.com/insilicomedicine/gentrl and in Supplementary Code.
References
Paul, S. M. et al. Nat. Rev. Drug Discov. 9, 203–214 (2010).
Avorn, J. N. Engl. J. Med. 372, 1877–1879 (2015).
Goodfellow, I. et al. Generative adversarial nets. in Advances in Neural Information Processing Systems 2672–2680 (2014).
Mamoshina, P. et al. Mol. Pharm. 13, 1445–1454 (2016).
Sanchez-Lengeling, B. & Aspuru-Guzik, A. Science 361, 360–365 (2018).
Kadurin, A. et al. Oncotarget 8, 10883–10890 (2016).
Kadurin, A. et al. Mol. Pharm. 14, 3098–3104 (2017).
Gómez-Bombarelli, R. et al. ACS Cent. Sci. 4, 268–276 (2018).
Putin, E. et al. Mol. Pharm. 15, 4386–4397 (2018).
Putin, E. et al. J. Chem. Inf. Model. 58, 1194–1204 (2018).
Harel, S. & Radinsky, K. Mol. Pharm. 15, 4406–4416 (2018).
Polykovskiy, D. et al. Mol. Pharm. 15, 4398–4405 (2018).
Kuzminykh, D. et al. Mol. Pharm. 15, 4378–4385 (2018).
Segler, M. H. S. et al. Nature 555, 604–610 (2018).
Merk, D. et al. Mol. Inform. 37, 1–2 (2018).
Merk, D. et al. Commun. Chem. 1.1, 68 (2018).
Moll, S. et al. Biochim. Biophys. Acta Mol. Cell Res. https://doi.org/10.1016/j.bbamcr.2019.04.004 (2019).
Richter, H. et al. ACS Chem. Biol. 14, 37–49 (2019).
Elton, D. C. et al. Mol. Syst. Des. Eng. 4, 828–849 (2019).
Irwin, J. J. et al. J. Chem. Inf. Model. 52, 1757–1768 (2012).
Oseledets, I. V. SIAM J. Sci. Comput. 33, 2295–2317 (2011).
Williams, R. J. Mach. Learn. 8, 229–256 (1992).
Brown, N. et al. J. Chem. Inf. Model. 59, 1096–1108 (2018).
Guimaraes, G. L. et al. Objective-Reinforced Generative Adversarial Networks (ORGAN) for sequence generation models. Preprint at https://arxiv.org/abs/1705.10843 (2017).
Sanchez-Lengeling, B. et al. Optimizing distributions over molecular space. An Objective-Reinforced Generative Adversarial Network for Inverse-design Chemistry (ORGANIC). Preprint at https://chemrxiv.org/articles/ORGANIC_1_pdf/5309668 (2017).
Ritter, H. & Kohonen, T. Biol. Cybern. 61, 241–254 (1989).
Sammon, J. W. IEEE Trans. Comput. C-18, 401–409 (1969).
Rappe, A. K. J. Am. Chem. Soc. 114, 10024–10035 (1992).
Acknowledgements
The authors thank T. Oprea (University of New Mexico School of Medicine) for the valuable contributions, review, and assessment of the novelty of the intellectual property generated by GENTRL. The authors would like to thank NVIDIA Corporation and M. Berger for providing early access to the graphics processing equipment used for deep learning applications by Insilico Medicine. The authors acknowledge T. Lu, L. Duan, Y. Hu, and the WuXi AppTec chemistry team for providing chemical synthesis of the presented compounds. The authors thank S. Djuric, whose valuable comments informed further experiments.
Author information
Authors and Affiliations
Contributions
A. Zhavoronkov, Y.A.I., and A.A. led the project, designed and planned the experiments, and wrote the manuscript. M.S.V., V.A.A., A.V.A., and V.A.T. planned and performed computational chemistry experiments. D.A.P., M.D.K., A. Zholus, A.A., Y.V., R.R.S., and A. Zhebrak developed and implemented the GENTRL. L.I.M. curated chemical synthesis, and B.A.Z. collected and prepared the data. L.H.L., R.S., D.M., L.X., and T.G. helped write the manuscript. A.A.-G. provided manuscript and methodological feedback.
Corresponding author
Ethics declarations
Competing interests
A. Zhavoronkov, Y.A.I., A. Aliper, M.S.V., V.A.A., A.V.A., V.A.T., D.A.P., M.D.K., A. Zholus, A. Asadulaev, Y.V., A. Zhebrak, R.R.S., L.I.M., and B.A.Z. work for Insilico Medicine, a commercial artificial intelligence company. L.H.L., R.S., D.M., L.X., and T.G. work for WuXi AppTec, a commercial research organization. A.A.-G. is a cofounder and board member of, and consultant for, Kebotix, an artificial intelligence-driven molecular discovery company and a member of the science advisory board of Insilico Medicine.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Integrated supplementary information
Supplementary Figure 1
Generative Tensorial Reinforcement Learning model.
Supplementary Figure 2 Smoothed representation of the General Kinase and Trending SOMs.
(a) Representation of Trending SOM, a Kohonen-based reward function that discriminates “novel” compounds from “old” compounds considering the application priority date of lead compounds disclosed in patents by major pharmaceutical companies. (b) Representation of neurons populated with kinase inhibitors. (c) Representation of neurons populated by molecules with no experimental activity against kinases. (d) Neurons were selected based on PF (circles) and subsequently were used for reward. Within the Specific Kinase SOM (not depicted) we observed that DDR1 inhibitors were distributed in the ensemble of topographically proximal neurons. Finally, we selected those structures which were located in DDR1 associated neurons.
Supplementary Figure 3 Pharmacophore hypotheses.
(a) 3-Centered pharmacophore hypothesis: Acc - hydrogen bond acceptor (r = 2Å), Hyd|Aro - hydrophobic or aromatic center (r = 2Å), Hyd - hydrophobic center (r = 2Å). (b) 4-Centered pharmacophore hypothesis: Acc - hydrogen bond acceptor (r = 2Å), Hyd|Aro - hydrophobic or aromatic center (r = 2Å), Hyd - hydrophobic center (r = 2Å), Acc|Specific - hydrogen bond acceptor or a fragment with similar spatial geometry (e.g. double or triple bond, planar cycle) (r = 1.7Å). Non-depicted distances are the same as for 3-centered pharmacophore. (c) 5-Centered pharmacophore hypothesis containing the same points that are highlighted in b above with an additional hydrophobic feature. Non-depicted distances are the same as for 3-centered and 4-centered pharmacophores. Yellow: the reported small-molecule DDR1 inhibitor (PDB code: 5BVN).
Supplementary Figure 4 Non-linear Sammon map.
The selected 40 molecules are marked by orange triangles. Areas of the best pharmacophore matching are highlighted by circles.
Supplementary Figure 5 The structures and dose-response curves for the generated molecules.
(a) Six generated compounds were tested in a dose-dependent manner against DDR1 tyrosine kinase. Compounds 1 and 2 demonstrated the IC50 values in the low nanomolar range. (b) Compounds 2 and 4 were additionally rescreened towards DDR1 kinase using another biochemical assay (Thermo Fisher-PR6913A) and have demonstrated the IC50 values of 37.12 and 155.6 nM respectively (below). Measure of center is mean, error bars are s.d. (n=2 for each experiment).
Supplementary Figure 6 Selectivity profile for compound 1 against 44 kinases panel.
The inhibition percent versus 44 non-target kinases was measured at 10μM concentration. The highest inhibition potency(%INH=37) within the panel was revealed against eEF-2K.
Supplementary Figure 7 Inhibition of DDR1 auto-phosphorylation in U2OS cells stimulated with collagen.
Representative blots of phosphorylated DDR1-Y513 in U2OS cells stimulated with collagen and treated with DDR1 inhibitors at different doses. Dasatinib was served as a positive control. Dasatinib, compounds 1 and 2 inhibited auto-phosphorylation in a dose-dependent manner. Experiments were repeated at least once and similar results were obtained.
Supplementary Figure 8 Effects of compounds 1 and 2 on cellular fibrosis markers α-actin and CCN2 (normalized to GAPDH) in MRC-5 cells.
Representative blots of produced α-actin and CCN2 in MRC-5 cells treated with TGF-b in the presence of DDR1 inhibitors at different doses. SB25334 and dasatinib were served as a positive control. Dasatinib and compound 1 suppressed α-actin and CCN2 production at the concentration of 10 μM. SB25334 inhibited α-actin production at the dose of 10 μM. Experiments were repeated at least once and similar results were obtained.
Supplementary Figure 9 Effects of compounds 1 and 2 on cellular fibrosis markers collagen I, α-actin and CCN2 (normalized to GAPDH) in LX-2 cells.
Representative blots of produced collagen I, α-actin and CCN2 in LX-2 cells treated with TGF-b in the presence of DDR1 inhibitors at different doses. SB25334 was served as a positive control. SB25334 and compound 1 suppressed collagen I production in a dose dependent manner. SB25334 inhibited α-actin production at the dose of 10 μM. Experiments were repeated at least once and similar results were obtained.
Supplementary Figure 10
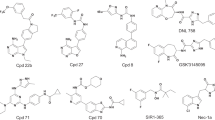
Examples of molecules that were rejected during the prioritization step.
Supplementary information
Supplementary Information
Supplementary Figures 1–10, Supplementary Table 1–10 and Supplementary Note
Supplementary Data Set
The 30,000 structures generated by GENTRL for the DDR1 kinase
Rights and permissions
About this article
Cite this article
Zhavoronkov, A., Ivanenkov, Y.A., Aliper, A. et al. Deep learning enables rapid identification of potent DDR1 kinase inhibitors. Nat Biotechnol 37, 1038–1040 (2019). https://doi.org/10.1038/s41587-019-0224-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41587-019-0224-x
This article is cited by
-
Pocket Crafter: a 3D generative modeling based workflow for the rapid generation of hit molecules in drug discovery
Journal of Cheminformatics (2024)
-
Reinvent 4: Modern AI–driven generative molecule design
Journal of Cheminformatics (2024)
-
Invalid SMILES are beneficial rather than detrimental to chemical language models
Nature Machine Intelligence (2024)
-
Machine learning for antimicrobial peptide identification and design
Nature Reviews Bioengineering (2024)
-
3D molecular generative framework for interaction-guided drug design
Nature Communications (2024)