Abstract
Angiosperms are the cornerstone of most terrestrial ecosystems and human livelihoods1,2. A robust understanding of angiosperm evolution is required to explain their rise to ecological dominance. So far, the angiosperm tree of life has been determined primarily by means of analyses of the plastid genome3,4. Many studies have drawn on this foundational work, such as classification and first insights into angiosperm diversification since their Mesozoic origins5,6,7. However, the limited and biased sampling of both taxa and genomes undermines confidence in the tree and its implications. Here, we build the tree of life for almost 8,000 (about 60%) angiosperm genera using a standardized set of 353 nuclear genes8. This 15-fold increase in genus-level sampling relative to comparable nuclear studies9 provides a critical test of earlier results and brings notable change to key groups, especially in rosids, while substantiating many previously predicted relationships. Scaling this tree to time using 200 fossils, we discovered that early angiosperm evolution was characterized by high gene tree conflict and explosive diversification, giving rise to more than 80% of extant angiosperm orders. Steady diversification ensued through the remaining Mesozoic Era until rates resurged in the Cenozoic Era, concurrent with decreasing global temperatures and tightly linked with gene tree conflict. Taken together, our extensive sampling combined with advanced phylogenomic methods shows the deep history and full complexity in the evolution of a megadiverse clade.
Similar content being viewed by others
Main
Flowering plants (angiosperms) represent about 90% of all terrestrial plant species2 but, despite their remarkable diversity and ecological importance underpinning almost all main terrestrial ecosystems, their evolutionary history remains incompletely known. Since their Mesozoic origins5,10,11, angiosperms have had a pervasive influence on the biosphere of Earth, shaping climatic changes at global and local scales12, supporting the structure and assembly of biomes13 and influencing the diversification of other organisms, such as insects, fungi and birds14. The evolution of terrestrial biodiversity is thus inextricably linked with the macroevolution of angiosperms, which can only be shown using a robust and comprehensive tree of life. Reconstructing such a tree, however, is challenging because of the sheer diversity of angiosperms and the complex phylogenetic signal in their genomes.
High-throughput DNA sequencing methods now enable us to reconstruct phylogenetic trees that broadly represent the evolutionary signal across entire genomes. Target sequence capture15 has revolutionized plant phylogenetics by unlocking herbarium specimens as a source of sequenceable DNA16, thus removing the chief sampling bottleneck that has obstructed the completion of the tree of life. Although previous work on plants has relied primarily on the widely sequenced plastid genome3,4,7, these technologies now allow us to tap into the evolutionary signal of the much larger and more complex nuclear genome. Universal nuclear probe sets, such as Angiosperms353 (ref. 8), have made target sequence capture consistently applicable across broad taxonomic scales, opening doors to collaboration and data integration17. As a result, opportunities now present themselves to address fundamental questions in plant evolutionary biology, such as the origin of angiosperms, the tempo and mode of their diversification and the classification of main lineages.
Here, we present a nuclear phylogenomic tree that includes all 64 orders and 416 families of angiosperms recognized by the prevailing classification18, using the Angiosperms353 (ref. 8) gene panel. Our sampling of 7,923 angiosperm genera (represented by 9,506 species) amounts to a 15-fold increase compared to previous work9. Leveraging a dataset of 200 fossil calibrations, we scale the tree to time, effectively capturing evolutionary divergences for all but the most recent 15% of angiosperm history. Although our tree broadly supports relationships predicted by previous studies primarily based on plastid data, it also shows previously unknown relationships and highlights some that remain intractable despite a vast increase in data. Gene tree conflict is tightly linked to diversification across the tree. We find evidence for high levels of conflict associated with an early burst of diversification, which is followed by an extended period of constant diversification rates underpinned by a tapestry of varied lineage-specific patterns. Diversification then increases in the Cenozoic Era, potentially driven by global climatic cooling. Our results highlight the fundamental role of botanical collections in reconstructing the tree of life to illuminate long-standing questions in angiosperm macroevolution.
The angiosperm tree of life
Our phylogenetic tree includes 58% of the approximately 13,600 currently accepted genera of angiosperms (Fig. 1 and Supplementary Table 1; ref. 2). Together, the 7,923 genera encompass 85.7% of total known angiosperm species diversity. We produced data for 6,777 of these genera; before this study, 3,154 of these lacked publicly available genomic data, of which 393 lacked any form of DNA sequence data. For the remaining genera, data were obtained from public repositories. Sampling for this project was possible thanks to the collaborative effort of many biodiversity institutions from around the world, including 163 herbaria in 48 countries. More than one-third of species were sourced directly from herbarium specimens, some dating back nearly 200 years. Many phylogenetically problematic lineages with unconventional genome evolution were sampled, such as holoparasites, mycoheterotrophs and aquatics. Many of the species included are threatened and four are extinct (or extinct in the wild). The resulting tree of life presented here is one of the largest genomic trees generated yet for angiosperms as a whole.
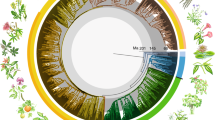
All 64 orders, all 416 families and 58% (7,923) of genera are represented. The young tree is illustrated here (maximum constraint at the root node of 154 Ma), with branch colours representing net diversification rates. Black dots at nodes indicate the phylogenetic placement of fossil calibrations based on the updated AngioCal fossil calibration dataset. Note that calibrated nodes can be older than the age of the corresponding fossils owing to the use of minimum age constraints. Arcs around the tree indicate the main clades of angiosperms as circumscribed in this paper. ANA grade refers to the three consecutively diverging orders Amborellales, Nymphaeales and Austrobaileyales. Plant portraits illustrating key orders were sourced from Curtis’s Botanical Magazine (Biodiversity Heritage Library). These portraits, by S. Edwards, W. H. Fitch, W. J. Hooker, J. McNab and M. Smith, were first published between 1804 and 1916 (for a key to illustrations see Supplementary Table 2). A high-resolution version of this figure can be downloaded from https://doi.org/10.5281/zenodo.10778206 (ref. 55).
The phylogenomic challenge
Large genomic datasets present challenges to phylogenetic inference. One issue is accurate homology assessment, which proved intractable across the full span of our dataset, even with the most advanced multiple sequence alignment methods. Another challenge is the efficient search of tree space based on gene matrices that have many more taxa than characters. We overcame both challenges with a divide-and-conquer approach (Supplementary Fig. 1). First, we computed a backbone species tree with sampling limited to five species per family (1,336 (15%) samples in total) and targeted to represent their deepest nodes (Supplementary Fig. 2). We used the backbone species tree to delimit taxon subsets for the construction of order-level gene alignments, which were then merged into global alignments. We then computed global gene trees from the global alignments, using backbone gene trees (inferred during the estimation of the backbone species tree) as topological constraints to reduce tree space while still letting gene trees differ from each other. The smaller number of samples in the backbone dataset permits a more thorough search of tree space, resulting in greater confidence at deeper nodes than could be achieved in an unconstrained global analysis. This approach allows a trade-off between comprehensive sampling and tree search robustness while accommodating putative discordance among gene trees. Finally, we used the global gene trees to generate a global species tree in a multispecies coalescent framework (Supplementary Fig. 3).
A widespread concern in phylogenomic analysis is the presence of undetected gene copies. Our findings are unlikely to be affected by this because we used genes that have been selected to be mostly single-copy across green plants8,9. Although gene duplication cannot be ruled out19, the methods we used have been shown to be robust to the presence of paralogues20. In addition, a full assessment of orthologues was not computationally tractable but should be undertaken when methods become available to fully unravel the complexity of genome evolution at this scale21.
Phylogenetic insights from nuclear data
Our results broadly corroborate the prevailing understanding of angiosperm phylogenetic relationships, which rests on three decades of molecular systematic research largely built on data from the plastid genome3,4,18,22. We recover all main lineages of angiosperms, namely Amborellales, Nymphaeales, Austrobaileyales, Ceratophyllales and the three larger clades, monocots, magnoliids (including Chloranthales) and eudicots (Figs. 1 and 2). Although some of the relationships among those groups, such as the placement of Amborellales as sister group to all other angiosperms, are well-established and confirmed here, others, such as the placement of Ceratophyllales, which have been unstable in previous work4,9, remain inconclusive in our results. Despite the contrasting biological properties of the nuclear and plastid genomes (for example, size, copy number, mode of inheritance, recombination and evolutionary rate), which can lead to conflicting phylogenetic results, our findings largely support the mostly plastid-based phylogenetic classification of the Angiosperm Phylogeny Group18 (Extended Data Fig. 1). For example, 58 of the 64 now accepted orders and 406 of the 416 families are recovered as monophyletic (excluding artefacts; Supplementary Table 1). The most striking exception is the non-monophyly of Asteraceae, the largest angiosperm family comprising the sunflowers and their relatives. Our tree also confirms 85% of the relationships among families recovered by ref. 4 using plastid genomes (Supplementary Fig. 4).
The overall stability of established relationships is unevenly distributed across the tree, as observed in contrasting patterns in the main eudicot clades, the asterids and rosids, which account for 35% and 29% of angiosperm diversity, respectively2. The relationships among main orders of asterids are stable9, with a clade comprising Ericales and Cornales sister to all other asterids and the remaining 15 orders divided in two main clades (campanulids and lamiids), both long characterized by their contrasting floral ontogeny23. Relationships contrasting with the status quo are mostly restricted to small orders, such as the paraphyly of Aquifoliales, Bruniales and Icacinales. These DNA-defined orders were consistently recovered as highly supported clades in plastome analyses4,24 but they lack morphological cohesion. Given their placement in our phylogenetic tree and unique morphologies, these changes, although small, will alter our understanding of the evolution of asterids.
By contrast to asterids, our findings in rosids conflict markedly with plastid-based evidence. First, we resolve Saxifragales, rather than Vitales4, as sister to the remainder of rosids. In rosids, the fabid and malvid subclades, recovered as reciprocally monophyletic by plastid data4,22, are substantially rearranged into a grade of four orders subtending two well-supported sister clades, which we designate here as the recircumscribed fabids and malvids. The new fabid clade (Cucurbitales, Fabales, Fagales and Rosales) has long been characterized by symbiotic nitrogen fixation25. In the new malvids (Brassicales, Celastrales, Huerteales, Malpighiales, Malvales, Oxalidales, Picramniales and Sapindales), Oxalidales is resolved as two independent lineages, the core emerging closer to Brassicales, Malvales and Sapindales, whereas Huaceae emerges in the position conventionally occupied by Oxalidales, that is, closer to Malpighiales and Celastrales (the former Celastrales–Oxalidales–Malpighiales (COM) clade18).
Notwithstanding the many well-supported confirmatory and new findings, some key relationships remain contentious and cannot be resolved by our data. These areas of high gene tree conflict often coincide with biological processes that confound phylogenetic inference. For example, the uncertain placements of eudicot orders Caryophyllales, Dilleniales and Gunnerales are probably impacted by key whole genome duplications9,26. The poor support for relationships among magnoliids, monocots, eudicots and Ceratophyllales might be explained by ancient hybridization events, such as that recently proposed for the origin of the monocots27. These examples highlight the importance of areas of poor resolution as waymarkers to biological events meriting further study.
Time frame for angiosperm macroevolution
Our tree was analysed in combination with a dataset of 200 fossil calibrations (originally described in ref. 5, with modifications) to estimate divergence times and rates of diversification. Because the age of angiosperms is uncertain28, we dated the tree with two different maximum constraints at the angiosperm crown node (154 and 247 million years ago (Ma), termed the young tree and old tree, respectively), which reflect realistic upper and lower bounds for the maximum age of this node5,28. These different constraints affected age estimates across angiosperms (Extended Data Fig. 2, Supplementary Fig. 5 and Supplementary Table 3). For example, in the young tree, stem node age estimates for Nymphaeales, Austrobaileyales and Ceratophyllales were 153, 152 and 152 Ma, respectively, whereas in the old tree the equivalent age estimates were 245, 244 and 243 Ma. Likewise, for larger clades such as magnoliids, monocots and eudicots, crown node age estimates were 151, 149 and 151 Ma in the young tree and 238, 237 and 241 Ma in the old tree. This range in age estimates is consistent with the most comprehensive comparable study5 (Extended Data Fig. 3) but our trees provide age estimates for a further 7,000 nodes. In subsequent analyses, we indicate if differing age estimates between the young tree and old tree cause substantially different interpretations of angiosperm diversification.
With our sampling across angiosperms, we ensured that deeper branching events leading to extant lineages are comprehensively represented, while recognizing that extinct lineages are inaccessible to genomic methods. However, our dated trees are sparsely sampled at the species-level, meaning that branching events are incompletely represented towards the present, limiting diversification inferences in that time window. To address this, we developed a simulation-based approach to quantify the sampling fraction through time. For both dated trees, the lineage representation begins to drop substantially (below 75%) around 50 Ma (Supplementary Fig. 6). However, the most dramatic fall in lineage representation occurs in the most recent 20 Myr, in which it falls from around 50% to slightly more than 1% at present. Our investigation of angiosperm diversification should be interpreted with this broader context in mind. In particular, inferences in the most recent 20 Myr may be updated in the future with denser species sampling.
The diversification of angiosperms
Diversification linked to gene conflict
We used our dated trees to reconstruct both diversification and gene tree conflict across a broad range of temporal and phylogenetic scales and investigate the relationship between them. We show that throughout angiosperm macroevolution, elevated gene tree conflict was tightly associated with elevated diversification. At a general level, this relationship is visible by simply comparing estimated diversification rates with gene tree conflict across all angiosperms through time (Fig. 3a). Meanwhile, in a branch-specific analysis using the temporal duration of branches as a proxy for the rate at which branches are diversifying, we also show that conflict and diversification rate are positively correlated (Extended Data Fig. 4) (P < 0.001, r2 = 0.51).
To characterize the theoretical basis of this relationship, we simulated species trees with corresponding gene trees under different diversification scenarios in a multispecies coalescent framework. These simulations showed that gene tree conflict is positively correlated with diversification when caused by incomplete lineage sorting, assuming that effective population size is constant (Supplementary Fig. 7). Our empirical results are largely consistent with such a scenario. Other potential causes of gene tree conflict such as whole genome duplication and hybridization may also be associated with rapid diversification and have been recorded extensively throughout angiosperms29,30. Overall, however, gene tree conflict seems to be reliable corroborating evidence for investigating temporal patterns of angiosperm diversification.
Early burst of angiosperm diversification
Our lineage-through-time (LTT) heatmap and diversification rate estimates through time both indicate an explosive early phase of diversification of extant lineages during the Late Jurassic and Early Cretaceous Periods (Fig. 2b and Fig. 3a). An early burst of angiosperm diversification, popularized as ‘Darwin’s abominable mystery’31,32, is expected given the sudden emergence of diverse angiosperm fossils during the Early Cretaceous11,33,34,35. Phylogenetic studies based on single or few genes have also implied that angiosperms diversified rapidly in the Early Cretaceous7,36,37,38. Our dated tree corroborates the existence of a distinct early burst of diversification, associated with high levels of gene tree conflict (Fig. 3a and Supplementary Fig. 8), further increasing our confidence in this finding.
The results illustrated are based on the young tree (maximum constraint at the root node of 154 Ma). a, Time-calibrated summary phylogenetic tree with LTT plots rendered as heatmaps for all orders with four or more sampled genera. The log-transformed increase in the number of lineages is depicted in 5 Myr intervals, omitting crown nodes, which disproportionately altered the visualization; crown node locations are indicated by vertical lines. The yellow to blue colour scale represents steep to shallow slopes. For each order, the numbers of sampled and total genera are provided. b, A global LTT heatmap for all angiosperms is shown at the bottom of the figure as a whole.
The results illustrated are based on the young tree (maximum constraint at the root node of 154 Ma). See Extended Data Fig. 5 for results based on the old tree. a, Estimated net diversification rate through time (yellow, left y axis) and the level of gene tree conflict through time (blue, right y axis). Net diversification rates are estimated with a model that enables speciation rates to vary between time intervals; the line is the posterior mean and the yellow shaded area is the 95% highest posterior density. Gene tree conflict is calculated from the percentage of gene trees that do not share a congruent bipartition with each species tree branch, with the plotted value being the mean across all species tree branches that cross each 2.5 Myr time slice. b, Cumulative percentage of extant orders and families that have originated through time. In both a and b, the background grey-scale gradient is the estimated percentage of extant lineages represented in the species tree through time (sampling fraction).
More than 80% of extant angiosperm orders originated during the early burst of diversification (Fig. 3b). Although not strictly comparable because of their subjective delimitation, orders represent the main components of angiosperm feature diversity, which have arisen rapidly after the crown node of angiosperms. In the young tree (Fig. 3), the early burst occurs during the Cretaceous, consistent with the hypothesis that a Cretaceous terrestrial revolution was triggered by the establishment of main angiosperm lineages14,39,40. More controversially, the old tree places the early burst in the Triassic Period (Extended Data Fig. 5), which is dramatically at variance with the palaeobotanical record33,34, highlighting that current molecular dating methods are unable to resolve the age of angiosperms28.
A tapestry of lineage-specific histories
Following the early burst, overall rates of diversification across angiosperms continued at a lower, constant pace for at least 80 Myr (Fig. 3a), during which time around three-quarters of all families originated (Fig. 3b). As expected, this phase of slower diversification was associated with lower levels of gene tree conflict. Despite the constancy of overall rates, diversification during this period was underpinned by a complex tapestry of lineage-specific patterns. This is illustrated by the LTT heatmap, which shows profound differences in diversification trajectories among orders (Fig. 2) and by the estimation of around 160 lineage-specific diversification rate shifts in angiosperms, most of which occur during this period. These rate shifts have a widespread phylogenetic distribution, with most orders containing at least one rate shift and many containing several nested shifts (Supplementary Table 4). The importance of nested rate shifts is highlighted extensively in discussions of evolutionary radiation41,42 and underpins the continual response of diversification to dynamic extrinsic and intrinsic conditions. However, because these rate shifts are temporally scattered, as also shown by ref. 43, they do not lead to observable global rate shifts across angiosperms.
A Cenozoic diversification surge
A second surge in angiosperm diversification occurred during the Cenozoic Era (Fig. 3a). The occurrence of this surge, despite the already high standing diversity of angiosperms at the time, suggests that diversification was unaffected by diversity-dependent processes, that is, the filling of available niche space as clades diversify44. Instead, this finding is consistent with previously proposed positive feedbacks between increased diversity and increased rates of diversification in angiosperms14, alongside more positive feedbacks, for example, between angiosperm and insect diversification45,46. Alternatively, global climatic cooling during the Cenozoic acting as a driver of angiosperm diversification could explain this finding7,47,48,49. Importantly, an even larger Cenozoic surge would probably be inferred with increased sampling that addresses the under-representation of branching events in the recent time window. The temporal distribution of lineage-specific diversification rate shifts may offer some insight into the cause of the Cenozoic surge. Many of the largest diversification rate increases occur during the Cenozoic, whereas the number of diversification rate decreases declines markedly during this period (Fig. 4). These large rate increases may underpin the Cenozoic surge. The expansion of taxon sampling should be given priority to confirm these patterns.
The results illustrated are based on the young tree (maximum constraint at the root node of 154 Ma). See Extended Data Fig. 6 for results based on the old tree. a, Diversification rate increases per LTT. The colour corresponds to the average magnitude of the rate increases during the time period. b, Equivalent to a but for rate decreases. c, Equivalent to a but focusing on the largest 25% of diversification rate increases. In a, b and c, the number of shifts is from the maximum a posteriori shift configuration with the prior for the number of shifts set to 10 and the background grey-scale gradient is the estimated percentage of extant lineages represented in the species tree through time (sampling fraction).
Synthesis
The nuclear phylogenomic framework presented here is the result of an ongoing initiative to complete the tree of life for all angiosperm genera50, a milestone in our understanding of angiosperm evolutionary relationships. This study not only sheds light on much of the deep diversification history of the angiosperms but also lays foundations for future work towards a species-level tree50. The standardized panel of nuclear genes in our dataset paves the way for more collaborations and data integration17,51, while the open availability of universal tools to sequence them (that is, Angiosperms353 probes8) has made nuclear genomic data more accessible at relatively low cost. The accelerating uptake of this approach52,53,54, which is readily applicable to herbarium collections16, indicates that large volumes of data will soon become available for a wide range of applications in plant diversity, systematic and macroevolutionary research.
Our fossil-calibrated, phylogenomic tree enables a range of unique insights into broad-scale diversification dynamics of angiosperms, substantiating the early burst of diversification anticipated by Darwin while illuminating the complexity and conflict in the lineage histories underlying it. This sets the scene for future research, extending these investigations to shallower phylogenetic scales or digging more deeply into the data to discover the processes driving angiosperm diversification, such as genomic conflict, polyploidy, selection, trait evolution and adaptation. The challenges brought by the scale of this dataset and its ongoing expansion may also catalyse the development of methods which take full advantage of the global proliferation of genomic data.
Methods
As part of the Plant and Fungal Trees of Life (PAFTOL) Project at the Royal Botanic Gardens, Kew50, we assembled a nuclear genomic dataset consisting of newly generated data and data mined from public repositories. Our objective was to sample at least 50% of all angiosperm genera, with genera selected in a phylogenetically representative manner on the basis of published research. To avoid excessive imbalance in the tree, we included only one sample per species and a maximum of three species per genus. When several samples were available for the same species, we selected those with the largest amount of data, that is, more genes and a higher sum of gene length. For genera with several species available, the criterion for selection was primarily phylogenetic representation followed by amount of data. One species of each gymnosperm family was selected to form the outgroup, totalling 12 samples.
We produced target sequence capture data for 7,561 samples using the universal Angiosperms353 probe set8 following established laboratory protocols50,56. We complemented our dataset with publicly available data for 2,054 species, sourced from the One Thousand Plant Transcriptomes Initiative9 (OneKP; 564 samples), annotated and unannotated genomes (151 samples) and the sequence read archive (SRA; 1,339 samples), the last including transcriptomes (for example, see refs. 57,58) and target capture data (for example, see refs. 59,60). To standardize taxonomy and nomenclature, all species names and families were harmonized with the World Checklist of Vascular Plants2 and orders with APG IV if possible18.
Sequence recovery
Sequence recovery was carried out in two ways, depending on the type of input data. For recovery on the basis of raw reads, that is, Angiosperms353 data or data mined from the SRA, we used HybPiper v.1.31 (ref. 61), embedded in a bespoke pipeline (https://github.com/baileyp1/PhylogenomicsPipelines). Raw reads were trimmed using Trimmomatic62 to remove low-quality bases and short sequences. In HybPiper, reads were initially binned into genes using BLASTN and an amino acid target file as reference (Supplementary File 1). Individual genes were assembled de novo using SPADES63 and refined by joining and trimming gene contigs to match coding regions using Exonerate64. For genes with paralogue warnings, only the putative orthologue as identified by HybPiper was used. Exclusion of genes with several copies per species has been shown to have negligible impact on species tree inference when it is performed under a multispecies coalescent framework, as described below20. Conversely, the inclusion of several copies per species would have rendered our study computationally intractable. Gene sequences from assembled genomes and OneKP transcriptomes were recovered using custom scripts described in ref. 50. Briefly, the assembled sequences were searched against the target file mentioned above using BLASTN, selecting the best match for each gene and trimming it to the BLAST hit. For a few Angiosperms353 samples that represented the sole accession of their respective families (Ixonanthes reticulata, Mitrastemon matudae and Tetracarpaea tasmannica) and had poor recovery from HybPiper (that is, below 5 kilobase pairs (kb) in total sum of contig length), recovery was undertaken following ref. 50, using less stringent recovery thresholds. The average recovery per order is presented in Supplementary Fig. 9.
Phylogenetic inference
To analyse the dataset, we devised a divide-and-conquer approach. First, we computed a backbone tree, sampling up to five species per family, to test the monophyly of orders and to rigorously explore deep relationships. We used the backbone tree to identify groups (orders or groups of orders) for multiple sequence alignment, with the aim of producing refined subalignments among closely related taxa. Subsequently, the subalignments were merged into global gene alignments and global gene trees were inferred from these using the respective gene trees from the backbone analysis as constraints. Finally, we inferred a multispecies coalescent tree using the estimated gene trees. The inference pipeline is summarized in Supplementary Fig. 1.
Backbone tree inference
The samples for the backbone were selected so as to represent the crown node and deepest divergences in each family. For families with five or fewer samples (279 families), all samples were included. For those with more than five samples (156), we selected the best sample (most genes and longest sequence) of each consecutively diverging clade (based on published phylogenetic evidence and preliminary analyses of our own data), until five samples were included. To evaluate the extent to which sample selection might affect the backbone tree topology, we inferred 20 backbone replicates, randomly selecting five samples for each family with more than five samples (among the 50% best samples in terms of gene number and gene length recovered). We then summarized the trees to family level and computed Robinson–Foulds distances between the backbone and the 20 replicates (Supplementary Fig. 10).
The phylogenetic reconstruction of the backbone involved up to two iterations of gene alignment and gene tree estimation, with an intermediate step of outlier removal. This was followed by species tree inference in a multispecies coalescent framework. In the first iteration, all sequences for a given gene were aligned using MAFFT v.7.480 (ref. 65) (with ffnsi method, that is, --retree 2 --maxiterate 1000) and with the direction of the sequence adjusted (--adjustdirection). After removing sites with more than 90% missing data with Phyutility66, gene trees were estimated using IQ-TREE v.2.2.0-beta67, keeping identical sequences in the analysis (--keep-ident), setting the substitution model to GTR + G and estimating branch support with 1,000 ultrafast bootstrap replicates68. Before the second iteration, we identified long branch outliers using TreeShrink69 in ‘all-genes’ mode and rerooting at the centroids of the trees. A second iteration of gene alignment, removal of gappy sites and gene tree estimation was performed for genes with outliers after the removal of outlier sequences. Subsequently, the resulting gene trees were summarized into a species tree using ASTRAL III v.5.7.3, a quartet-based species tree estimation method statistically consistent with the multispecies coalescent model70, enabling the full annotation option (-t 2), having first collapsed poorly supported nodes (ultrafast bootstrap ≤ 30%) in the input gene trees using Newick utilities71.
Order-level subalignments
For the order-level subalignments, most orders were analysed individually, following the same method described for the backbone. In some cases, smaller orders (fewer than 50 samples) were analysed together with larger ones if they formed monophyletic groups in the backbone. These groups are: (1) Commelinales with Zingiberales, (2) Dioscoreales with Pandanales, (3) Fagales with Fabales, (4) Columelliales, Dipsacales, Escalloniales and Paracryphiales with Apiales, (5) all magnoliids (Canellales, Laurales, Magnoliales and Piperales) and (6) all gymnosperms together (Cycadales, Ephedrales, Gnetales, Ginkgoales and Pinales). Conversely, orders emerging as non-monophyletic in the backbone were split into monophyletic subgroups as follows: (1) Cardiopteridaceae and Stemonuraceae separate from the rest of Aquifoliales, (2) Dasypogonaceae separate from the rest of Arecales, (3) Collumelliaceae separate from the rest of Bruniales, (4) Oncothecaceae separate from the rest of Icacinales and (5) Huaceae separate from the rest of Oxalidales. The groupings of samples used in the order-level subalignments are provided in Supplementary Table 1. Very small groups, comprising one or two samples (termed orphan sequences), were not included in subalignments and were incorporated directly in global analyses.
Global gene alignments and trees
We produced global gene alignments by merging the order-level subalignments (before removal of gappy sites) and adding the orphan non-aligned sequences using MAFFT65, with up to 100 refinement iterations. This approach yields alignment across the order-level subalignments without disrupting the structure in the subalignments. The final gene alignments were cleaned by removing gappy sites. A summary of the alignments was produced with AMAS72 (Supplementary Table 5) and the average occupancy per gene per order is presented in Supplementary Fig. 11.
We then estimated gene trees in Fasttree v.2.1.10 (ref. 73), setting the model to GTR + G, using pseudocounts to avoid biases from fragmentary sequences and increasing search thoroughness (-spr 4, -mlacc 2 and -slownni). We used the gene trees from the backbone analysis to constrain the topology of each respective global gene tree. To avoid propagating error from the backbone analysis to the global analysis, we removed potentially misleading signal from the backbone gene trees before applying them as constraints. First, branches with bootstrap values below 80% were collapsed to avoid enforcing poorly supported relationships. Second, tips placed far from the rest of their order were algorithmically removed (but retained in global gene alignments). Once global gene trees were estimated, outlier long branches were removed using TreeShrink and the set of pruned gene trees was used to compute the global species tree using ASTRAL-MP v.5.15.5 (ref. 74), after collapsing branches with poor support (that is, those with support lower than 10% in the Shimodaira–Hasegawa test).
Divergence time estimation
Divergence times were estimated by penalized likelihood in treePL75,76. This method is computationally efficient for datasets of this scale and typically estimates similar divergence times to more computationally intensive Bayesian analyses. The coalescent species tree topology was used as the input tree with molecular branch lengths estimated in IQ-TREE, on the basis of a concatenated alignment of the top 25 genes selected by SortaDate77. Genes were selected by ranking their corresponding gene trees according to the number of congruent bipartitions with the species tree. We selected genes on this basis because high gene tree conflict leads to error in divergence time estimates78,79.
Fossil calibrations were based on the AngioCal fossil calibration dataset described in ref. 5. We used an updated version of this dataset, referred to as AngioCal v.1.1 (Supplementary Table 6 and Supplementary File 2). Assigning fossil calibrations in this dataset to our tree topology led to 200 unique minimum age calibrations at internal nodes (Supplementary Table 7 and Supplementary Fig. 12). A maximum constraint of 154 or 247 Ma was used at the angiosperm crown node. These two values, respectively, represent a young and old constraint for the maximum age of the angiosperm crown node5,28. Both values are nonetheless considerably older than the oldest known crown group angiosperm fossils of around 127.2 Ma (ref. 80). Both maximum constraints, in combination with all the minimum age constraints, were used to time-calibrate the species tree. Depending on the maximum constraint at the root node, these dated phylogenetic trees are referred to as young tree and old tree, respectively. For both the young tree and old tree, four analyses were performed in treePL, using smoothing values of 0.1, 1, 10 or 100. These different smoothing values assume high to low levels of among-branch substitution rate variation.
Sampling extant lineages through time
At 1 Myr intervals from the root age of the dated phylogenetic trees to the present, we calculated how many angiosperm lineages would have been present in a hypothetical tree that sampled 100% of extant angiosperm species diversity. We used this to quantify the proportion of extant lineages incorporated by our phylogenetic trees through time (Supplementary Methods). To do this we simulated unsampled diversity on the dated trees: the species diversity of unsampled genera was simulated as a constant-rate birth–death branching process originating in the crown group of its respective family, whilst unsampled species diversity in sampled genera was simulated as a constant-rate birth–death branching process originating at the stem node of the relevant genus. The extant diversity of each simulated branching process was determined using the World Checklist of Vascular Plants2. At each time interval, we then calculated the proportional difference between the number of lineages in our dated phylogenetic tree and the hypothetical fully sampled tree.
Diversification rate estimation
Dated trees estimated with alternative smoothing values were very similar (Extended Data Fig. 2 and Supplementary Fig. 5), so diversification rate estimates were only performed with the dated trees estimated with a smoothing value of 10. By contrast, age estimates in the young and old trees differed markedly. Diversification rate estimates were therefore performed for both these dated trees. In each case, the dated trees were pruned such that there was a maximum of one tip for each genus.
An initial analysis of diversification rates was performed by generating LTT plots as heatmaps for angiosperms as a whole, as well as for each order, with colours representing the steepness of each LTT curve at 5 Myr intervals. To calculate the steepness of the curve, we calculated the running difference between logarithmic corrected cumulative sums of lineages and applied Tukey’s running median smoothing to avoid excessive noise. For order plots, the cumulative sum starts at the first branching point, that is, order crown nodes.
Time-dependent diversification parameters (speciation and extinction rates) were also explicitly estimated across all angiosperms. These analyses were performed in RevBayes with the dnEpisodicBirthDeath function81. The smallest time windows in which rates were estimated were 5 Ma. However, larger windows were used toward the root of the tree such that there were at least 50 branching events in each time window. Three different models were used: equal rates of speciation and extinction across all windows; variable rates of speciation across windows but equal rates of extinction; and equal rates of speciation across windows but variable rates of extinction. Bayes factor comparison was used to compare models and offered strong support for the variable rate models but could not distinguish between the two variable rate models (Supplementary Information), indicating that they are probably from the same congruent set of models for the species tree82. In subsequent discussion we primarily refer to results from the variable speciation rate model (for justification see Supplementary Information), although both variable rate models estimate similar patterns of net diversification rates through time (Supplementary Information).
Lineage-specific diversification rate estimation was performed in BAMM83 and RevBayes. For analyses in BAMM, the setBammPriors function from the R package BAMMtools84 was used to define appropriate priors. Different sets of analyses were performed with the prior for the expected number of shifts set to either 10 or 100. These different prior settings had minimal effect on parameter estimates. Clade-specific sampling fractions were specified for each sampled family and a backbone sampling fraction of 1 was used. We therefore accounted for incomplete sampling within families alongside comprehensive sampling of the backbone of the tree. For analyses in RevBayes, the dnCDBDP function was used and the prior for the total number of rate shifts was set to either 10 or 100. Clade-specific sampling fractions cannot be specified with this function. Therefore, the sampling fraction was set to 1 meaning that estimates will become inaccurate toward the present because of unsampled within-family diversity.
Simulations on gene tree conflict
Simulations were based on a multispecies coalescent process. Each species tree contained 100 tips and was simulated as a birth–death branching process with time-dependent rates of speciation and extinction. In experiment 1, the extinction rate was always 0. The speciation rate was 0.75 species Myr−1 at times over 6 Ma, between 6 and 2 Ma the speciation rate was 0.075 species Myr−1 and less than 2 Ma the speciation rate was 0.75 species Myr−1. In experiment 2, the net diversification rates were the same as in experiment 1; however, in this case changes to the extinction rate led to the net diversification rate shifts. Therefore, for all time intervals, the speciation rate was 0.75 species Myr−1. At times over 6 Ma the extinction rate was 0 species Myr−1, between 6 and 2 Ma the extinction rate was 0.675 species Myr−1 and at times less than 2 Ma the extinction rate was 0 species Myr−1.
Species trees with extinct lineages have extra complexities: first, changes in the extinction rate have a less direct impact on the duration of extant lineages in the species tree compared to changes in the speciation rate (Supplementary Information); and second, the effect of extinction is reduced at times close to the present. This causes shorter branches in the species tree, leading to the so-called ‘pull of the present’. We therefore performed a further analysis that was similar to experiment 2 but with no decrease in the extinction rate at the present. This offered insight into the effect of the ‘pull of the present’ on inferences of gene tree conflict and diversification rates and the relationship between these variables and the timing of rate shifts.
One-hundred gene trees were simulated along the branches of the birth–death branching processes according to a multispecies coalescent process. For most experiments, the effective population size was 5,000. In one further experiment, which was otherwise the same as experiment 1, the effective population size was 50,000. For each simulated dataset, the degree to which the simulated gene trees exhibited conflicting topologies with the species tree was plotted through time (Supplementary Information). This enabled characterization of the relationship between gene tree conflict caused by incomplete lineage sorting and shifts in speciation and extinction rates in the species tree.
More methods, results and discussion are available (Supplementary Information; Supplementary Figs. 13–24 and Supplementary Table 8).
Inclusion and ethics statement
The research described here results from a highly inclusive, large-scale, international collaboration, which has actively encouraged the participation of many individuals from around the world. The authorship comprises many nationalities and is representative in terms of gender, career stage and career path. A total of 163 herbaria from 48 countries provided samples and/or house herbarium vouchers related to samples used in the study (see Acknowledgements). These samples originated from many countries, including Indigenous lands. We recognize the complex histories underlying all natural history collections and the global challenge we face in acknowledging them. We gave priority to recently collected samples and, as a result, most (85%) date from the postcolonial era (estimated here as 1970 onward). To share the benefits of our research, all data generated through this collaboration have been made publicly available before the submission of this work in several data releases, starting in 2019 (see Data availability).
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
All raw DNA sequence data generated for this study are deposited in the European Nucleotide Archive under the following bioprojects PRJNA478314, PRJEB35285, PRJEB49212 and PRJNA678873. All analysed data and metadata are available in Zenodo at https://doi.org/10.5281/zenodo.10778206 (ref. 55). The resulting trees and metadata are also available in GBIF (https://doi.org/10.15468/4njn8b) and Open Tree of Life (https://tree.opentreeoflife.org/curator/study/view/ot_2304). The names used in this work match the World Checklist of Vascular Plants (https://doi.org/10.34885/jdh2-dr22).
Code availability
The code used and developed to perform analyses is available in GitHub at https://github.com/RBGKew/AngiospermPhylogenomics and Zenodo at https://doi.org/10.5281/zenodo.10778206 (ref. 55).
References
Diamond, J. Evolution, consequences and future of plant and animal domestication. Nature 418, 700–707 (2002).
Govaerts, R., Nic Lughadha, E., Black, N., Turner, R. & Paton, A. The World Checklist of Vascular Plants, a continuously updated resource for exploring global plant diversity. Sci. Data 8, 215 (2021).
Chase, M. W. et al. Phylogenetics of seed plants: an analysis of nucleotide sequences from the plastid gene rbcL. Ann. Missouri. Bot. Gard. 80, 528–580 (1993).
Li, H.-T. et al. Plastid phylogenomic insights into relationships of all flowering plant families. BMC Biol. 19, 232 (2021).
Ramírez-Barahona, S., Sauquet, H. & Magallón, S. The delayed and geographically heterogeneous diversification of flowering plant families. Nat. Ecol. Evol. 4, 1232–1238 (2020).
Li, H.-T. et al. Origin of angiosperms and the puzzle of the Jurassic gap. Nat. Plants 5, 461–470 (2019).
Dimitrov, D. et al. Diversification of flowering plants in space and time. Nat. Commun. 14, 7609 (2023).
Johnson, M. G. et al. A universal probe set for targeted sequencing of 353 nuclear genes from any flowering plant designed using k-medoids clustering. Syst. Biol. 68, 594–606 (2019).
One Thousand Plant Transcriptomes Initiative. One thousand plant transcriptomes and the phylogenomics of green plants. Nature 574, 679–685 (2019).
Barba-Montoya, J., dos Reis, M., Schneider, H., Donoghue, P. C. J. & Yang, Z. Constraining uncertainty in the timescale of angiosperm evolution and the veracity of a Cretaceous Terrestrial Revolution. New Phytol. 218, 819–834 (2018).
Doyle, J. A. Molecular and fossil evidence on the origin of angiosperms. Annu. Rev. Earth Planet. Sci. 40, 301–326 (2012).
Holbourn, A. E. et al. Late Miocene climate cooling and intensification of southeast Asian winter monsoon. Nat. Commun. 9, 1584 (2018).
Pennington, R. T., Cronk, Q. C. B. & Richardson, J. A. Introduction and synthesis: plant phylogeny and the origin of major biomes. Philos. Trans. R. Soc. Lond. B 359, 1455–1464 (2004).
Benton, M. J., Wilf, P. & Sauquet, H. The Angiosperm terrestrial revolution and the origins of modern biodiversity. New Phytol. 233, 2017–2035 (2022).
Dodsworth, S. et al. Hyb-Seq for flowering plant systematics. Trends Plant Sci. 24, 887–891 (2019).
Brewer, G. E. et al. Factors affecting targeted sequencing of 353 nuclear genes from herbarium specimens spanning the diversity of angiosperms. Front. Plant Sci. 10, 1102 (2019).
Baker, W. J. et al. Exploring Angiosperms353: an open, community toolkit for collaborative phylogenomic research on flowering plants. Am. J. Bot. 108, 1059–1065 (2021).
The Angiosperm Phylogeny Group. et al. An update of the Angiosperm Phylogeny Group classification for the orders and families of flowering plants: APG IV. Bot. J. Linn. Soc. 181, 1–20 (2016).
Joyce, E. M. et al. Phylogenomic analyses of Sapindales support new family relationships, rapid Mid-Cretaceous Hothouse diversification and heterogeneous histories of gene duplication. Front. Plant Sci. 14, 1063174 (2023).
Yan, Z., Smith, M. L., Du, P., Hahn, M. W. & Nakhleh, L. Species tree inference methods intended to deal with iIncomplete lineage sorting are robust to the presence of paralogs. Syst. Biol. 71, 367–381 (2022).
Watanabe, T., Kure, A. & Horiike, T. OrthoPhy: a program to construct ortholog data sets using taxonomic information. Genome Biol. Evol. 15, evad026 (2023).
Ruhfel, B. R., Gitzendanner, M. A., Soltis, P. S., Soltis, D. E. & Burleigh, J. G. From algae to angiosperms—inferring the phylogeny of green plants (Viridiplantae) from 360 plastid genomes. BMC Evol. Biol. 14, 23 (2014).
Endress, P. K. Origins of flower morphology. J. Exp. Zool. 291, 105–115 (2001).
Stull, G. W., Duno de Stefano, R., Soltis, D. E. & Soltis, P. S. Resolving basal lamiid phylogeny and the circumscription of Icacinaceae with a plastome-scale data set. Am. J. Bot. 102, 1794–1813 (2015).
Soltis, D. E. et al. Chloroplast gene sequence data suggest a single origin of the predisposition for symbiotic nitrogen fixation in angiosperms. Proc. Natl Acad. Sci. USA 92, 2647–2651 (1995).
Walker, J. F. et al. From cacti to carnivores: improved phylotranscriptomic sampling and hierarchical homology inference provide further insight into the evolution of Caryophyllales. Am. J. Bot. 105, 446–462 (2018).
Guo, X. et al. Chloranthus genome provides insights into the early diversification of angiosperms. Nat. Commun. 12, 6930 (2021).
Sauquet, H., Ramírez-Barahona, S. & Magallón, S. What is the age of flowering plants? J. Exp. Bot. 73, 3840–3853 (2022).
Landis, J. B. et al. Impact of whole-genome duplication events on diversification rates in angiosperms. Am. J. Bot. 105, 348–363 (2018).
Tank, D. C. et al. Nested radiations and the pulse of angiosperm diversification: increased diversification rates often follow whole genome duplications. New Phytol. 207, 454–467 (2015).
Darwin, C. The Correspondence of Charles Darwin (Cambridge Univ. Press, 1879).
Buggs, R. J. A. Reconfiguring Darwin’s abominable mystery. Nat. Plants 8, 194–195 (2022).
Coiro, M., Doyle, J. A. & Hilton, J. How deep is the conflict between molecular and fossil evidence on the age of angiosperms? New Phytol. 223, 83–99 (2019).
Herendeen, P. S., Friis, E. M., Pedersen, K. R. & Crane, P. R. Palaeobotanical redux: revisiting the age of the angiosperms. Nat. Plants 3, 17015 (2017).
Friis, E. M., Crane, P. R. & Pedersen, K. R. Early Flowers and Angiosperm Evolution (Cambridge Univ. Press, 2011).
Davies, T. J. et al. Darwin’s abominable mystery: insights from a supertree of the angiosperms. Proc. Natl Acad. Sci. USA 101, 1904–1909 (2004).
Magallón, S., Gómez-Acevedo, S., Sánchez-Reyes, L. L. & Hernández-Hernández, T. A metacalibrated time-tree documents the early rise of flowering plant phylogenetic diversity. New Phytol. 207, 437–453 (2015).
Mathews, S. & Donoghue, M. J. The root of angiosperm phylogeny inferred from duplicate phytochrome genes. Science 286, 947–950 (1999).
Dilcher, D. Toward a new synthesis: major evolutionary trends in the angiosperm fossil record. Proc. Natl Acad. Sci. USA 97, 7030–7036 (2000).
Meredith, R. W. et al. Impacts of the Cretaceous terrestrial revolution and KPg extinction on mammal diversification. Science 334, 521–524 (2011).
Bouchenak-Khelladi, Y., Onstein, R. E., Xing, Y., Schwery, O. & Linder, H. P. On the complexity of triggering evolutionary radiations. New Phytol. 207, 313–326 (2015).
Donoghue, M. J. & Sanderson, M. J. Confluence, synnovation and depauperons in plant diversification. New Phytol. 207, 260–274 (2015).
Magallón, S., Sánchez-Reyes, L. L. & Gómez-Acevedo, S. L. Thirty clues to the exceptional diversification of flowering plants. Ann. Bot. 123, 491–503 (2019).
Rabosky, D. L. Diversity-dependence, ecological speciation and the role of competition in macroevolution. Annu. Rev. Ecol. Evol. Syst. 44, 481–502 (2013).
Asar, Y., Ho, S. Y. W. & Sauquet, H. Early diversifications of angiosperms and their insect pollinators: were they unlinked? Trends Plant Sci. 27, 858–869 (2022).
Peris, D. & Condamine, F. L. The dual role of the angiosperm radiation on insect diversification. Nat. Commun. 15, 552 (2024).
Folk, R. A. et al. Rates of niche and phenotype evolution lag behind diversification in a temperate radiation. Proc. Natl Acad. Sci. USA 116, 10874–10882 (2019).
Sun, M. et al. Recent accelerated diversification in rosids occurred outside the tropics. Nat. Commun. 11, 3333 (2020).
Soltis, P. S., Folk, R. A. & Soltis, D. E. Darwin review: angiosperm phylogeny and evolutionary radiations. Proc. R. Soc. B 286, 20190099 (2019).
Baker, W. J. et al. A comprehensive phylogenomic platform for exploring the angiosperm tree of life. Syst. Biol. 71, 301–319 (2022).
McDonnell, A. J. et al. Exploring Angiosperms353: developing and applying a universal toolkit for flowering plant phylogenomics. Appl. Plant Sci. 9, e11443 (2021).
Bratzel, F. et al. Target-enrichment sequencing reveals for the first time a well-resolved phylogeny of the core Bromelioideae (family Bromeliaceae). TAXON 72, 47–63 (2023).
Gagnon, E. et al. Phylogenomic discordance suggests polytomies along the backbone of the large genus Solanum. Am. J. Bot. 109, 580–601 (2022).
Murillo-A, J., Valencia-D, J., Orozco, C. I., Parra-O, C. & Neubig, K. M. Incomplete lineage sorting and reticulate evolution mask species relationships in Brunelliaceae, an Andean family with rapid, recent diversification. Am. J. Bot. 109, 1139–1156 (2022).
Zuntini, A.R. & Carruthers, T. Phylogenomics and the rise of the angiosperms. Zenodo https://doi.org/10.5281/zenodo.10778206 (2024).
Hendriks, K. P. et al. Global Brassicaceae phylogeny based on filtering of 1,000-gene dataset. Curr. Biol 33, 4052–4068 (2023).
Chen, L.-Y. et al. Phylogenomic analyses of Alismatales shed light into adaptations to aquatic environments. Mol. Biol. Evol. 39, msac079 (2022).
Timilsena, P. R. et al. Phylogenomic resolution of order- and family-level monocot relationships using 602 single-copy nuclear genes and 1375 BUSCO genes. Front. Plant Sci. 13, 876779 (2022).
Ogutcen, E. et al. Phylogenomics of Gesneriaceae using targeted capture of nuclear genes. Mol. Phylogenet. Evol. 157, 107068 (2021).
Yardeni, G. et al. Taxon-specific or universal? Using target capture to study the evolutionary history of rapid radiations. Mol. Ecol. Resour. 22, 927–945 (2022).
Johnson, M. G. et al. HybPiper: extracting coding sequence and introns for phylogenetics from high-throughput sequencing reads using target enrichment. Appl. Plant Sci. 4, 1600016 (2016).
Bolger, A. M., Lohse, M. & Usadel, B. Trimmomatic: a flexible trimmer for Illumina sequence data. Bioinformatics 30, 2114–2120 (2014).
Bankevich, A. et al. SPAdes: a new genome assembly algorithm and its applications to single-cell sequencing. J. Comput. Biol. 19, 455–477 (2012).
Slater, G. S. C. & Birney, E. Automated generation of heuristics for biological sequence comparison. BMC Bioinformatics 6, 31 (2005).
Katoh, K. & Standley, D. M. MAFFT Multiple Sequence Alignment Software Version 7: improvements in performance and usability. Mol. Biol. Evol. 30, 772–780 (2013).
Smith, S. A. & Dunn, C. W. Phyutility: a phyloinformatics tool for trees, alignments and molecular data. Bioinformatics 24, 715–716 (2008).
Minh, B. Q. et al. IQ-TREE 2: new models and efficient methods for phylogenetic inference in the genomic era. Mol. Biol. Evol. 37, 1530–1534 (2020).
Hoang, D. T., Chernomor, O., von Haeseler, A., Minh, B. Q. & Vinh, L. S. UFBoot2: improving the ultrafast bootstrap approximation. Mol. Biol. Evol. 35, 518–522 (2018).
Mai, U. & Mirarab, S. TreeShrink: fast and accurate detection of outlier long branches in collections of phylogenetic trees. BMC Genomics 19, 272 (2018).
Zhang, C., Rabiee, M., Sayyari, E. & Mirarab, S. ASTRAL-III: polynomial time species tree reconstruction from partially resolved gene trees. BMC Bioinformatics 19, 153 (2018).
Junier, T. & Zdobnov, E. M. The Newick utilities: high-throughput phylogenetic tree processing in the Unix shell. Bioinformatics 26, 1669–1670 (2010).
Borowiec, M. L. AMAS: a fast tool for alignment manipulation and computing of summary statistics. PeerJ 4, e1660 (2016).
Price, M. N., Dehal, P. S. & Arkin, A. P. FastTree 2—approximately maximum-likelihood trees for large alignments. PLoS ONE 5, e9490 (2010).
Yin, J., Zhang, C. & Mirarab, S. ASTRAL-MP: scaling ASTRAL to very large datasets using randomization and parallelization. Bioinformatics 35, 3961–3969 (2019).
Sanderson, M. J. Estimating absolute rates of molecular evolution and divergence times: a penalized likelihood approach. Mol. Biol. Evol. 19, 101–109 (2002).
Smith, S. A. & O’Meara, B. C. treePL: divergence time estimation using penalized likelihood for large phylogenies. Bioinformatics 28, 2689–2690 (2012).
Smith, S. A., Brown, J. W. & Walker, J. F. So many genes, so little time: a practical approach to divergence-time estimation in the genomic era. PLoS ONE 13, e0197433 (2018).
Britton, T. Estimating divergence times in phylogenetic trees without a molecular vlock. Syst. Biol. 54, 500–507 (2005).
Carruthers, T. et al. The implications of incongruence between gene tree and species tree topologies for divergence time estimation. Syst. Biol. 71, 1124–1146 (2022).
Gomez, B., Daviero-Gomez, V., Coiffard, C., Martín-Closas, C. & Dilcher, D. L. Montsechia, an ancient aquatic angiosperm. Proc. Natl Acad. Sci. USA 112, 10985–10988 (2015).
Höhna, S. et al. RevBayes: Bayesian phylogenetic inference using graphical models and an interactive model-specification language. Syst. Biol. 65, 726–736 (2016).
Louca, S. & Pennell, M. W. Extant timetrees are consistent with a myriad of diversification histories. Nature 580, 502–505 (2020).
Rabosky, D. L. Automatic detection of key innovations, rate shifts and diversity-dependence on phylogenetic trees. PLoS ONE 9, e89543 (2014).
Rabosky, D. L. et al. BAMMtools: an R package for the analysis of evolutionary dynamics on phylogenetic trees. Methods Ecol. Evol. 5, 701–707 (2014).
Acknowledgements
The PAFTOL project was funded by grants from the Calleva Foundation to the Royal Botanic Gardens, Kew. Data were also contributed by the Genomics for Australian Plants Framework Initiative consortium funded by Bioplatforms Australia (enabled by the National Collaborative Research Infrastructure Strategy) and partner organizations. The work was further supported by research grants from VILLUM FONDEN (grant no. 00025354) and the Aarhus University Research Foundation (grant no. AUFF-E-2017-7-19) to W.L.E. and from grant nos NSF DBI 1930030 and DEB 1917146 to S.A.S. Computational resources and technical support were provided by the Research/Scientific Computing teams at The James Hutton Institute and the National Institute of Agricultural Botany (NIAB) through the ‘UK’s Crop Diversity Bioinformatics HPC’ (BBSRC grant no. BB/S019669/1). The following provided technical assistance to the project at various stages: O. Berry, N. Black, M. Corcoran, S. Dequiret, I. Fairlie, L. Frankel, T. Freeth, A. Gilbert, B. Lepschi, D. Lewis, L. May, A. McArdle, E. O’Loughlin, S. Phillips, T. Sarkinen, L. Simmons, N. Walsh and M.-H. Weech. We thank all institutions who made their biological collections available and the many botanists and co-workers in the field who have collected, identified and curated the specimens used in this project. Specifically, we thank the following herbaria and their staff for providing samples for genomic analysis and/or for housing voucher specimens associated with analysed samples: A, ABH, AD, ALTB, APSC, B, BA, BC, BCN, BCRU, BG, BH, BHCB, BISH, BJFC, BKF, BM, BNRH, BOL, BONN, BR, BRI, BRIT, BRLU, BRUN, C, CAN, CANB, CAS, CBG, CNS, COL, CONC, CORD, CS, CTES, CUVC, DNA, E, EA, F, FI, FLAS, FMB, FTG, G, GB, GC, GENT, GH, GOET, GUAY, GZU, HAW, HEID, HITBC, HNG, HO, HPUJ, HRCB, HTW, HUA, HUAL, HUAZ, HUB, HUEFS, HUFU, IBSC, IBUG, ICN, IEB, INB, INPA, JBB, JBL, JRAU, K, KAS, KLU, KRB, KUN, L, LE, LISC, LP, LPB, LYJB, M, MA, MAU, MBA, MBML, MEDEL, MEL, MELU, MHA, MICH, MIN, MJG, MO, MSUN, MT, MY, N, NBG, NCU, NCY, NE, NH, NHM, NHMR, NMNL, NOU, NSW, NU, NY, OS, OSBU, P, PERTH, PG, PH, PRE, PTBG, QBG, QCA, QRS, RB, REU, S, SALA, SAR, SEV, SGO, SI, SING, SP, SPF, SPFR, SUVA, TCD, TEX, TNS, TUH, TUM, U, UAPC, UB, UBT, UDW, UEC, UPCB, UPR, UPS, UPTC, US, USM, W, WAG, WS, WTU, YA and ZSS; acronyms follow Index Herbariorum (https://sweetgum.nybg.org/science/ih/). We also thank the Millennium Seed Bank Partnership for supporting access to samples. We acknowledge all national, state and regional authorities who authorized and facilitated the sourcing of these specimens. See also extended acknowledgements in the Supplementary Information.
Author information
Authors and Affiliations
Contributions
A.R.Z., T.C., A.A., S. Bellot, D.M.C., O.M.G., P.J.K., I.J.L., H. Sauquet, S.A.S., W.L.E., F. Forest and W.J.B were involved in conceptualization of this work. A.R.Z., T.C., A.A., S. Bellot, D.M.C., O.M.G., H. Sauquet, S.A.S., W.L.E., F. Forest and W.J.B. contributed to the methodology. A.R.Z., O.M., E.F., C. McGinnie, S.R.R., L. Simpson, J.J.C., R.S.C., S.D., L. Pokorny, G.M.A., K.G., K.P.H., A. Hoewener, A.-Q.H., E.M.J., I.A.B.S.K., I.L., D.A.L., E. J. Lírio, J.-X.L., P. Malakasi, N.A.S.P., T.S., J.V., G.K.A., R.L.A., M.S.A., M.A., M.J.A., J.A., W.A., J.B.B., C.D.B., H.F.B., M.D.B., R.L.B., R.J.B., M.J.B., E. Biffin, N.B., J.L.B., D.B., R.B., A.M.C.B., P. C. Boyce, G.L.C.B., M. Briggs, L. Broadhurst, G.K.B., J.J.B., A.B., S. Buerki, E. Burns, M. Byrne, S. Cable, A.C., M. W. Callmander, Á.C., D.J.C., W.M.C.-M., M.M.C., A.J.A.C., A.C.M., M. W. Chase, L.W.C., M.C., S. Chen, M.J.M.C., P.-A.C., M.A.C., S.C.C., J.G.C., X.C., T.L.P.C., I.D.C., L.C., I.D., G.D., N.M.J.D., A.P.D., K.-J.D., S.R.D., M.F.D., M.R.D., S.L.E., U.E., R.H.J.E., M. Escudero, M. Estrella, F. Fabriani, M.F.F., P.L.F., S.Z.F., R.M.F., S.F., L.F., T.F., M.G.-C., E.M.G., D.A.G., A. Giaretta, M.G., L.J.G., C.C.G., D.J.G., S.W.G., A. Grall, L.G., B.F.G., D.G.G., J.H., T. Haevermans, A. Haigh, J.C.H., T. Hall, M.J.H., S.A.H., O.H., T.R.H., G.D.H., H.C.F.H., C.J.J., S.A.J., R.W.J., G.K., I.M.K., K.K., M.K., E.A.K., G.J.K., B.K., B.B.K., R.R.K., S.K., M.A.K., J.H.L.-M., F.L., C.J.L., É.L.-B., G.P.L., D.-Z.L., L.L., S.L.-S., T.L., D.L., M. Lu, P.L.-I., J.L., E. J. Lucas, M. Luján, M. Lum, T.D.M., C. Magdalena, V.F.M., L.E.M., S.J.M., K. McColl, A.J.M., A.E.M., T.G.B.M., H.M., R.I.M., V.S.F.T.M., F.A.M., J.D.M., A.K.M., M.J.M., T.L.M., K. Mummenhoff, J.M., P. Muriel, D.J.M., K.N., L.N., F.J.N., R. Nyffeler, A.O., E.M.O., L. Palazzesi, A.L.P., S.K.P., J.P., D.S.P., O.A.P.-E., C. Persson, M.P., Y.P., J.R.P., G.M.P., R.F.P., G.T.P., C. Puglisi, M.Q., R.K.R., P.E.J.R., M. Renner, E.H.R., M. Rodda, Z.S.R., S.R., R.R., M.F.S., H. Schaefer, R. J. Schley, A.S.-L., A.S., I.S., K.A.S., M.P.S., A.O.S., A.R.G.S., M.S., E.C.S., J.F.S., N.S., D.E.S., P.S.S., R. J. Soreng, C.A.S., J.R.S., P.F.S., S.C.K.S., L. Struwe, J.M.T., I.R.H.T., A.H.T., I.T., A.T.-B., F.U., T.M.A.U., J.C.V., G.A.V., H.P.V., M.S.V., J.M.V., N.W., M.W., C.A.D.W., A.J.W., J.J.W., L.T.W., T.C.W., S.Y.W., L.A.W., R.W., S.W., M.X., Y.Y., Y.-X.Z., M.-Y.Z., S.Z., F.O.Z., S. Bellot, D.M.C., O.M.G., H. Sauquet, W.L.E., F. Forest and W.J.B. provided resources. A.R.Z., T.C., O.M., P. C. Bailey, K.L., G.E.B., N.E., E.F., B.G.-P., C. McGinnie, S.R.R., L. Simpson, L. Botigué, J.J.C., R.S.C., S.D., M.G.J., J.T.K., L. Pokorny, N.J.W., G.M.A., L.D., K.G., K.P.H., A. Hoewener, A.-Q.H., E.M.J., I.A.B.S.K., I.L., D.A.L., E. J. Lírio, J.-X.L., P. Malakasi, N.A.S.P., T.S., J.V. and S. Bellot carried out the investigations. A.R.Z., T.C., O.M., G.E.B., N.E., E.F., B.G.-P., C. McGinnie, R. Negrão, S.R.R., L. Simpson, E.T.R., V.M.A.B., K.P.H., J.V., T.R.A. and H. Sauquet were responsible for data curation. A.R.Z., T.C., P. C. Bailey and K.L. conducted the formal analysis. A.R.Z., T.C., P. C. Bailey, K.L., M.G.J. and J.T.K. developed the software. A.R.Z., T.C. and R. Negrão prepared the visualizations. A.R.Z., T.C., W.L.E., F. Forest and W.J.B. wrote the original manuscript with support from A.A., S. Bellot, D.M.C., O.M.G., H. Sauquet and S.A.S. K.L., E.F., J.J.C., J.T.K., L. Pokorny, N.J.W., A.-Q.H., E.M.J., I.L., J.V., M.S.A., J.B.B., M.D.B., R.L.B., A.M.C.B., L. Broadhurst, A.B., D.J.C., M.M.C., M. W. Chase, L.W.C., M.J.M.C., P.-A.C., T.L.P.C., U.E., R.H.J.E., M. Estrella, M.F.F., P.L.F., M.G., L.J.G., S.W.G., J.H., T. Haevermans, J.C.H., O.H., T.R.H., K.K., E.A.K., M.A.K., F.L., C.J.L., D.-Z.L., S.L.-S., T.D.M., V.S.F.T.M., F.A.M., A.K.M., M.J.M., D.J.M., F.J.N., L. Palazzesi, J.P., D.S.P., O.A.P.-E., Y.P., G.M.P., R.K.R., R.R., H. Schaefer, A.S.-L., M.P.S., A.R.G.S., N.S., D.E.S., P.S.S., R. J. Soreng, P.F.S., S.C.K.S., A.H.T., T.M.A.U., J.M.V., J.J.W., T.C.W., Y.Y., S.Z. and I.J.L. reviewed the final manuscript. S.A.S., W.L.E., F. Forest and W.J.B. undertook supervision. P.J.K., I.J.L., F. Forest and W.J.B. acquired funding. V.M.A.B., P.J.K., I.J.L., F. Forest and W.J.B. were responsible for project administration.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Craig Barrett, Elena Kramer, Patrick Wincker and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Tanglegram at ordinal level between this work (left) and the APG IV schematic tree (right).
Branches colours represent the clades according to the composition proposed in each work. Posterior probability is presented only for nodes without maximum support. Coloured circles in the left tree represent the posterior probability of each node as: maximum (absent), between 1 and 0.95 (green), between 0.95 and 0.75 (yellow), between 0.75 and 0.5 (red), below 0.5 (black).
Extended Data Fig. 2 Comparison of node age estimates in the eight time-calibrated phylogenetic trees.
Each point represents a node and corresponds to the percentage difference in age estimates for that node between the two trees that are compared in each plot.
Extended Data Fig. 3 Comparison of stem ages of families and orders inferred in this study and Ramírez-Barahona et al.5.
a and b, Stem age comparison between our young tree (maximum constraint at the root node of 154 Ma) and the dataset CC_complete of Ramírez-Barahona et al.5. a, Ages in each study, coloured according to taxonomic rank and b, Age differences, calculated as age in this study minus age in Ramírez-Barahona et al.5 c and d, Stem ages comparison between our old tree (maximum constraint at the root node of 247 Ma) and the dataset UC_complete from Ramírez-Barahona et al.5 c, Ages in each study, coloured according to taxonomic rank and d, Age differences, calculated as age in this study minus age in Ramírez-Barahona et al.5.
Extended Data Fig. 4 Correlation between branch time duration and percentage of gene trees that do not share a congruent bipartition for the branch.
The results are based on the young tree (maximum constraint at the root node of 154 Ma). For each branch in the young tree, the percentage of gene trees that do not share a congruent bipartition with the species tree branch is plotted against the logarithm of the time duration for the branch.
Extended Data Fig. 5 Angiosperm-wide diversification and gene tree conflict through time.
This is equivalent to Fig. 3 but for the old tree (maximum constraint at the root node of 247 Ma). a, Estimated net diversification rate through time (yellow, left y-axis) and the level of gene tree conflict through time (blue, right y-axis). Net diversification rates are estimated with a model that enables speciation rates to vary between time intervals; the line is the posterior mean and the yellow shaded area is the 95% highest posterior density. Gene tree conflict is calculated from the percentage of gene trees that do not share a congruent bipartition with each species tree branch, with the plotted value being the mean across all species tree branches that cross each 2.5 Myr time slice. b, Cumulative percentage of extant orders and families that have originated through time. In both a and b, the background grey-scale gradient is the estimated percentage of extant lineages represented in the species tree through time (“sampling fraction”).
Extended Data Fig. 6 Summary of lineage-specific diversification rate shifts estimated by BAMM.
This is equivalent to Fig. 4, but for the old tree (maximum constraint at the root node of 247 Ma). a, Diversification rate increases per lineage through time. The colour corresponds to the average magnitude of the rate increases during the time period. b, Equivalent to a, but for rate decreases. c, Equivalent to a, but focusing on the largest 25% of diversification rate increases. In a, b and c, the number of shifts is extracted from the maximum a posteriori shift configuration, the prior for the number of shifts is set to 10 and the background grey-scale gradient is the estimated percentage of extant lineages represented in the species tree through time (“sampling fraction”).
Supplementary information
Supplementary Information
Supplementary Methods, Results, Discussion, references, Figs. 1–24, captions for Tables 1–8, Files 1 and 2 and extended acknowledgements.
Supplementary Tables
Supplementary Tables 1–8.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zuntini, A.R., Carruthers, T., Maurin, O. et al. Phylogenomics and the rise of the angiosperms. Nature 629, 843–850 (2024). https://doi.org/10.1038/s41586-024-07324-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-024-07324-0
This article is cited by
-
ANAgdb: a multi-omics and taxonomy database for ANA-grade
BMC Plant Biology (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.