Abstract
The tokamak approach, utilizing a toroidal magnetic field configuration to confine a hot plasma, is one of the most promising designs for developing reactors that can exploit nuclear fusion to generate electrical energy1,2. To reach the goal of an economical reactor, most tokamak reactor designs3,4,5,6,7,8,9,10 simultaneously require reaching a plasma line-averaged density above an empirical limit—the so-called Greenwald density11—and attaining an energy confinement quality better than the standard high-confinement mode12,13. However, such an operating regime has never been verified in experiments. In addition, a long-standing challenge in the high-confinement mode has been the compatibility between a high-performance core and avoiding large, transient edge perturbations that can cause very high heat loads on the plasma-facing-components in tokamaks. Here we report the demonstration of stable tokamak plasmas with a line-averaged density approximately 20% above the Greenwald density and an energy confinement quality of approximately 50% better than the standard high-confinement mode, which was realized by taking advantage of the enhanced suppression of turbulent transport granted by high density-gradients in the high-poloidal-beta scenario14,15. Furthermore, our experimental results show an integration of very low edge transient perturbations with the high normalized density and confinement core. The operating regime we report supports some critical requirements in many fusion reactor designs all over the world and opens a potential avenue to an operating point for producing economically attractive fusion energy.
Similar content being viewed by others
Main
Fusion energy is the ultimate energy source for humanity16. A promising approach is a steady-state fusion reactor using magnetic confinement in the tokamak configuration17,18. With a deeper understanding of tokamak plasma physics and the development of reactor-relevant technologies, many fusion reactor designs have been proposed3,4,5,6,7,8,9,10. When the ion temperature is above 13 keV (1.5 × 108 K) in D–T fusion reactions, the thermonuclear power density19 Pfus = nfuel2⟨σv⟩E/4 is proportional to the fuel density (nfuel) squared, as the change of normalized reaction rate ⟨σv⟩ with temperature is relatively small. Here, E is the fusion energy released per reaction. Detailed definitions of all variables mentioned in this paper can be found in Extended Data Table 1. Therefore, to achieve attractive fusion goals, most of the recent fusion pilot plant (FPP) designs require very high plasma densities, higher than the empirical edge density limit known as the Greenwald density11 (nGr), in tokamak high-confinement mode (H-mode) plasmas13. The energy confinement quality, represented by the H-factor20 (for example, H98y2), is believed to be the highest leverage parameter for fusion capital cost8. H98y2 is usually required to exceed the standard H-mode level (H98y2 = 1.0) for good fusion economy. FPP designs3,4,5,6,7,8,9,10 simultaneously require 1 ≤ Greenwald fraction (fGr) ≤ 1.3 and 1 ≤ H98y2 ≤ 1.65. However, such a tokamak operating regime is an uncharted area that has never been verified in experiments.
The empirical nGr is a density limit for the pedestal density in an H-mode plasma21,22. The pedestal is a narrow region of plasma at the edge with suppressed turbulent transport and a steep pressure gradient. When approaching nGr at the pedestal, various unfavourable phenomena can be observed in experiments. These cause a strong decrease of the confinement quality or even a sudden, complete loss of plasma energy (disruption)22. A peaked core density profile is, therefore, required to achieve a line-averaged density above the pedestal density limit. Possible approaches include relying on the natural peaking at low collisionality23 and the potential inward particle pinch24. The previous DIII-D experiment24 can achieve a transient fGr of about 1.4 with D2 gas puffing. A large pinch velocity has been measured. H98y2 in this case is around 1. ASDEX Upgrade experiments took a different approach by using pellet injection to improve the core fuelling. The experimental results show a transient fGr ≈ 1.5 with pellet injection25,26. However, the H98y2 values in those discharges were less than 1. More examples with H98y2 < 1 at high density are well documented22. As no tokamak experiment has yet attained a sustained fGr above 1 and H98y2 well above 1 (for example, 1.5) at the same time, experimentally verifying the desired operating regime in FPP designs is a great challenge for the magnetic confinement fusion community.
Another challenge with H-mode reactor plasmas is the very high transient heat load produced by quasi-periodic edge magnetohydrodynamic (MHD) instabilities known as type-I edge-localized-modes (ELMs). Without control, ELMs in a reactor can severely damage plasma-facing-components, for example, the first wall27,28. ELM control is an active research area and various approaches have been proposed29,30,31,32,33. However, compatibility among small/no ELM solutions, high density (above nGr) and high confinement quality (H98y2 well above 1, for example, 1.5) has not been demonstrated in experiments.
We report a new experimental approach for achieving a line-averaged density above nGr. It exploits an operating regime recently established in the DIII-D tokamak that allows simultaneous fGr > 1.0, H98y2 ≈ 1.5 and small ELMs and could support many existing designs for future reactors3,4,5,6,7,8,9,10. The approach elevates the plasma density in the core while keeping the pedestal fraction of the Greenwald density at moderate levels (for example, fGr,ped ≈ 0.7), thus not violating the empirical density limit. It does so by exploiting self-organized internal transport barriers (ITBs) at large minor radius in the high poloidal-beta (βP) scenario15,34,35,36. More information about the high-βP research can be found in Methods. In experiments, the on-axis fraction of the Greenwald density (fGr,0) can reach up to 1.7, resulting in a line-averaged fGr of 1.3. ITBs in the density and temperature profiles also greatly improve the energy confinement quality (H98y2 up to 1.8), compared to the standard H mode (H98y2 = 1) at the same engineering and operating parameters.
Figure 1 shows a plot of the DIII-D database and illustrates the progress made in extending the plasma operating space towards high fGr and high H98y2. The 2019 high-βP experiments with impurity injection15 have simultaneously achieved fGr > 1.0 and H98y2 > 1.0. However, in these experiments, too much impurity injection also increases the radiative energy loss in the plasma core, limiting H98y2 at high density. Of the violet diamonds in Fig. 1, some have H98y2 ≤ 1.2 when fGr ≥ 1.15. However, these results are not good enough for FPP designs. A major improvement in the 2022 DIII-D high-βP experiment used additional D2 gas puffing (Fig. 2) instead of impurity injection. This approach effectively reduces the core radiation and improves H98y2, as shown in Fig. 1 (blue squares). Thus, this paper reports a clear experimental demonstration of an accessible operating point in an existing tokamak that can meet a few of the FPP requirements, including simultaneous fGr > 1 and H98y2 ≈ 1.5. For comparison, other scenarios presented run on DIII-D have not achieved such simultaneous normalized performance (yellow circles).
More than 3,600 discharges are included. Violet diamonds show high-βP experiments performed in 2019 with impurity injection. Blue squares are the new high-βP experiments performed in 2022 without impurity injection. Yellow circles represent all other experiments performed in 2019–2022. The area shaded in orange indicates the parameter space for attractive FPP designs. Vertical and horizontal dashed lines show fGr = 1.0 and H98y2 = 1.0, respectively.
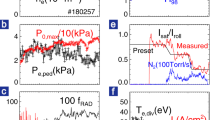
a, fGr in blue and H98y2 in green. b, βN in blue, βP in green and q95 in violet. c, D2 gas puffing in feedback control in black and dedicated feedforward D2 gas puffing in vermillion. d, Peak pedestal electron density gradient in blue and pedestal total pressure in vermillion. e, Separatrix electron density in green and ratio between pedestal electron density and separatrix electron density in violet. f–i, Profiles of electron temperature (f), ion temperature (g), electron density (h) and carbon density (i) at the time slices shown in the vertical dashed lines in a. Dots with error bars are measurements. j–l, Dα data for the three periods shown in the shaded area in d. a.u., arbitrary units. m–o, Total pressure profiles at the time slices of the vermillion dots in d.
Figure 2 shows detailed data from an example discharge (190904) in 2022. The striking feature in this discharge is the dynamic synergy between energy confinement quality and plasma density. That is, H98y2 increased along with fGr (Fig. 2a) until the ramping down of the heating power (Extended Data Fig. 1e). This is opposite to the common observation of reduced energy confinement quality in higher density H modes22, especially for experiments close to the Greenwald density. The plasma was maintained at fGr > 1.0 and H98y2 > 1.0 for about 2.2 s, which was 2.2 times the current diffusion time (τR) or 24 times the energy confinement time (τE). Thus, the high normalized density and confinement phase was not transient, which is imperative for application in future long-pulse FPPs. A normalized plasma pressure βN ≈ 3.5 and βP ≈ 2.9 was achieved at safety factor q95 ≈ 8.5 (Fig. 2b) with plasma current Ip = 0.73 MA and toroidal magnetic field BT = 1.89 T, and with mixed co- and counter-Ip neutral beam injection (NBI). Note that nGr = 6.7 × 1019 m−3 in this discharge, close to the Greenwald density of the ITER 9 MA steady-state scenario at 7.2 × 1019 m−3. The dedicated D2 gas puffing time trace is shown in vermillion in Fig. 2c. This approach ensures that there is a sufficient source of particles in the plasma, and it pushes the plasma density to a higher level, regardless of the change in the feedback gas (black line in Fig. 2c).
Profiles of the temperature and density for electrons, deuterium (main ion) and carbon (main impurity) are shown in Fig. 2f–i and Extended Data Fig. 2a. The evolution of the on-axis densities for electrons, deuterium and carbon is displayed in Extended Data Fig. 1c. One can see that ITBs developed in all density channels. The increased deuterium density in this experiment suggests the promising application of this scenario in future FPPs, as it can attain a higher fuel density to give a higher fusion power. A related piece of experimental evidence is shown in Extended Data Fig. 1d. It is clear that with increased plasma density and energy confinement, the neutron rate, an indicator of fusion performance, increased substantially (67% higher, from 0.6 × 1015 to 1.0 × 1015 s−1) from 2 to 4.8 s, whereas the injected power (blue line in Extended Data Fig. 1e) was almost constant. Moreover, a very mild increase of the radiated power was observed in the very-high-density phase of the experiment (Extended Data Fig. 1e). The core radiated power as a fraction of the injected power increased from 10% to 20% as fGr increased from 0.7 to 1.1. The edge radiation remained about 25% of the injected power. Note that for either Bremsstrahlung radiation or impurity line emission, the radiated power was roughly proportional to the electron density squared. Therefore, some increase in the radiated power was expected even with the same impurity level, when the plasma density was increased significantly. Regarding the impurity behaviour, one can see a well-developed ITB at large radius in the carbon density profiles (Fig. 2i). Despite the ITB at large radius, the carbon density inside the ITB did not have a significant central peak, which would usually cause a large amount of core radiation and a reduction of core performance. The ratio between carbon density and electron density stayed around 4–5% during the evolution (Extended Data Fig. 2b). This is consistent with the well-controlled radiated power in the phase with fGr > 1.0.
The evolution of the safety factor profile (q-profile) is shown in Extended Data Fig. 2c. The figure shows the self-organized q-profile evolution, which reflects the change of the local bootstrap current density associated with the development of a large-radius ITB. The local minimum q (qmin) in the outer half of the plasma was at ρ ≈ 0.6 for around 2τR. qmin in this discharge stayed above 2.
When a density ITB built up over time and was sustained, the total pedestal pressure at ρ = 0.88 did not change significantly (Fig. 2d). However, other pedestal parameters and the ELM behaviour changed. At fGr < 0.8, typical standard H-mode pressure profiles and typical large type-I ELMs were observed (Fig. 2j,m). At 0.8 ≤ fGr < 1.0, pressure profiles with an ITB and compound ELMs emerged (Fig. 2k,n). Finally, pressure profiles with a large ITB and small ELMs dominated the fGr ≥ 1.0 phase (Fig. 2l,o). During the evolution, a decreased peak pedestal electron density (ne,ped) gradient, increased separatrix electron density (ne,sep) and decreased ratio between ne,ped and ne,sep were observed, as shown in Fig. 2d,e. These parameter evolutions are consistent with the favourable conditions needed to access the small-ELM regime discussed in the literature29. A more detailed modelling analysis of the pedestal for different ELM behaviours will be discussed later in this paper.
Although addressing the transient heat load is crucial, mitigating the stationary heat load is equally important for an FPP. Divertor detachment is widely considered to be a necessary solution for realizing an acceptable stationary heat load in the operation of future FPPs. Even without detachment-oriented impurity seeding, Extended Data Fig. 3 shows that the electron temperature at the divertor plates (Te,div) clearly reduced from over 35 eV (before 1.8 s) to 20–25 eV (1.8–2.8 s) and finally to 10–15 eV (after 2.8 s) in the fGr > 1.0 and H98y2 ≈ 1.5 phase, and there were small ELMs. The lowest Te,div phase is consistent with the existence of an ITB at large radius. Although Te,div ≤ 15 eV is not yet considered as divertor detachment (usually Te,div < 10 eV), it already suggests that there would be mitigation of tungsten erosion under the experimental stationary heat load, if a tungsten wall had been used. Note that although the integration of full divertor detachment and high-confinement core has been achieved in previous DIII-D high-βP experiments and reported15,37, the experimental approach and the operating parameter space were both different. The previous results used impurity seeding and fGr ≈ 0.9, which are not sufficient for FPP designs.
Therefore, the analysed typical DIII-D high-βP discharge has demonstrated a sustained, accessible operating point in a present tokamak that integrates high normalized density and confinement quality, small ELMs and reduced divertor electron temperature, thus addressing the key requirements of FPP designs for simultaneous high-performance core and excellent core-edge integration.
To understand the physics that enables high confinement quality at high normalized density, we performed a gyro-fluid transport analysis using the TGLF code38 on the experimental data from the discharge shown in Fig. 2. Figure 3a,b shows the dependence of the normalized electron turbulent heat flux Qe/QGB (where QGB is the Gryo-Bohm heat flux) on the fractional contribution of the density gradient to the pressure gradient (Fp = T∇n/∇p) at mid-minor radius in the plasma. The gyro-fluid modelling indicates that when using either numerical approach to vary Fp (constant ∇T or constant ∇p), the decreasing trend of Qe for increasing Fp is robust. A similar result was obtained for the ion energy transport. These results reveal an important feature in the high-βP scenario, namely that anomalous turbulent transport, which leads to poor global confinement, can be reduced with a high density gradient, that is, a high density in the core with the pedestal density maintained below nGr. This is consistent with the experimental observation of synergy between high confinement quality and high density. If Fp were increased by 30%, the normalized Qe would decrease by a factor of 2 compared with the prediction at the experimental value, when the normalized pressure gradient αMHD (approximately −q2/BT,unit2Rdp/dr) was moderate (1.13), as shown in Fig. 3a. However, the reduction of the transport can be 2–3 orders of magnitude stronger when αMHD is high (2.75) in the experimental equilibrium (Fig. 3b). Note that this finding is also consistent with the previous nonlinear gyro-kinetic theoretical modelling39, which found an extreme reduction in the transport coefficient when high αMHD was combined with moderate density gradients. The underlying physics includes 1) the low drive of the ion-temperature-gradient turbulence at high density gradient (that is, there is a low ratio between the density gradient scale length and the ion temperature scale length (ηi)), and 2) less effective coupling between trapped electrons and the trapped-electron-mode turbulence owing to the much narrower turbulence eigenfunction at high αMHD.
a, Moderate αMHD case from the high-βP discharge in Fig. 2. Fp scan with the constant ∇p approach in blue and with the constant ∇T approach in vermillion. The experimental (Exp.) value of Fp is indicated by the black arrow. b, High αMHD case from the high-βP discharge in Fig. 2. Same colour coding as in a. c,d, Temperature (c) and density (d) profiles for the low-q95 H-mode case analysed in e and f. Dashed lines show the radial location for transport analysis. e,f, Two-dimensional scans of normalized electron turbulent heat flux on Fp and local q based on the low-q95 H-mode data shown in c and d. Full experimental βe (e) and half experimental βe (f). The experimental data point from the low-q95 discharge is indicated by a blue star in e.
We also applied the same gyro-fluid transport analysis to a standard H-mode discharge to reveal the requirement for realizing the favourable conditions for low transport at high density. A low-q95 standard H-mode discharge (DIII-D 187019) with strong D2 gas puffing and high density was investigated. Compared with the high-βP discharge discussed above, this discharge had the same heating power (9 MW), comparable line-averaged density (5.0–6.5 × 1019 m−3), slightly lower βN (approximately 2.5), but much lower q95 (4 versus 8.5). This was because of a much higher Ip (1.3 versus 0.73 MA). Typical standard H-mode profiles are shown in Fig. 3c,d, which are different from the ITB profiles in Fig. 2. Figure 3e presents the transport analysis of a two-dimensional scan on Fp and local q at ρ = 0.65. The modelling uses the experimental βe value. As illustrated by the horizontal dashed lines, the figure can be roughly divided into three regimes. At low local q, such as for the standard H-mode experimental data point, the modelling predicts high turbulent transport at high Fp. This is consistent with the experimental observation of decreased H98y2 at high density in this discharge. At medium q, transport is predicted to be almost independent of Fp. Finally, low transport at high Fp can be found in the high-q regime (top right corner of this figure highlighted by the blue dashed line). This example suggests that a minimum of the local q ≈ 4.4 is required to access this regime. Note that the analysed high-βP case has local q ≈ 5.1. However, high local q alone is insufficient to access this regime. Figure 3f indicates the importance of sufficient βe, or the plasma pressure (β). Note that β changes accordingly in the modelling when scanning βe. The range of the two-dimensional scan is the same. However, this scan uses half of the experimental βe in the modelling. As one can see, the results are significantly different. For most of the q values in the scan, high turbulent transport at high Fp is predicted. The favourable low transport at high Fp may still exist but probably requires very high local q, which is less realistic in present tokamak experiments or future machine designs.
In summary, the transport analysis suggests that the standard H-mode could access the favourable low-transport regime at high density, with the following necessary conditions: high local q and high plasma pressure β, which are two key components in the expression of αMHD. Thus, sufficient αMHD is essential for realizing the favourable operating regime. As summarized in the literature15,37,40, α-stabilization is considered as the primary turbulence suppression physics in the high-βP scenario, as it provides a reactor-relevant rotation-independent mechanism for high confinement40. On the other hand, given that βP ∝ βNq95, high q95 and high βN lead to high βP. Therefore, the high-βP scenario is naturally an excellent candidate for pursing this goal.
We performed a pedestal analysis to evaluate the pedestal stability and understand the evolution of the ELM behaviour in the high-βP discharge described in Fig. 2. The ELITE calculations41 shown in Fig. 4a predict the stability boundary for peeling–ballooning modes in the pedestal, for each of the three ELM states. In the type-I ELM state, the pedestal lies near the unstable ballooning region. Evolving to the small-ELM state, the experimental point moves along the ballooning boundary towards a lower pedestal pressure gradient and lower pedestal current density. Moving further away from the peeling boundary is consistent with the observation of no giant ELMs in the later phase. Modelling with BOUT++ (refs. 42,43,44) provides details on the instability growth rate in Fig. 4b. The dominant low-n peeling–ballooning mode was identified at n ≈ 10, which agrees with the ELITE result. The predicted low-n growth rate is smallest for small ELMs. BOUT++ modelling also resolves high-n resistive ballooning modes near the separatrix, when considering the plasma resistivity. It is clear that the high-n separatrix modes are dominant in the small-ELM case in contrast to other results in Fig. 4b. The modelling suggests that the high-n separatrix modes played an essential role in the observation of small ELMs in high-βP plasmas.
a,b, Results for the type-I ELM in blue, the compound ELM in green and the small ELM in violet. a, Pedestal stability versus normalized pedestal current density (y axis) and normalized pressure gradient at the pedestal peak gradient location (x axis). jmax, jsep and ⟨j⟩ are the maximum pedestal current density, the current density at the separatrix and the average current density in the pedestal region, respectively. Stability boundaries are shown as solid lines. Experimental points are indicated as open squares with error bars. b, Linear mode growth rate (normalized by Alfvén frequency, ωA) at different toroidal mode numbers.
In this paper, we have extended the operating space of a tokamak plasma towards a regime with simultaneous fGr up to 1.25 and H98y2 ≈ 1.3–1.8, using the high-βP scenario in DIII-D. The achievement of entering this previously uncharted regime provides essential support to many attractive FPP designs all over the world. The increased deuterium density and neutron rate in the experiment confirm the promising application of this scenario for higher fusion performance in future FPPs. Unlike many previous high-density H-mode experiments, the high-βP scenario uniquely features a synergy between high confinement quality and high density, especially around the Greenwald value. We have also elucidated the important role of α-stabilization in this achievement, showing that the favourable regime of low turbulent transport at high density is predicted and achieved only at relatively high local q and high β, namely for sufficient αMHD at high βP. This successful experiment not only addresses a few of the key requirements on FPP core plasma parameters but also suggests a potential solution for core-edge integration by demonstrating sustained small ELMs together with fGr > 1.0 and H98y2 > 1.0. Realizing the small-ELM regime is understood as a combination of the reduced growth rate of low-n modes and the predominance of the high-n resistive ballooning mode near the separatrix because of the decreased peak density gradient in the pedestal, increased separatrix density and high βP. During the natural small-ELM phase with a high normalized density and confinement, the plasma is close to divertor detachment, which is believed to be the most promising solution for achieving steady-state plasma–wall-interactions in FPPs37,45. The natural proximity of detachment conditions shows the potential of a fully integrated scenario with high-performance core and cool edge. As the divertor detachment was not optimized in the discussed experiment, doing so will be important work for future experiments. Note that the compatibility of the high-βP scenario with full divertor detachment has been demonstrated37. So far, neither a significant central peak in the density profile of the impurity (carbon) nor a significant increase in the core radiated power has been observed when the density is above the Greenwald value. Dedicated impurity transport experiments and modelling work are also under consideration for this operating regime. Fast-particle confinement is important for future FPPs. Experiments on the high-βP scenario in DIII-D usually exhibit classical fast-ion transport. More discussion of previous results is presented in ‘DIII-D high-βP experiments’ (Methods).
We fully appreciate that further work is needed to address other critical issues related to FPP compatibility, for example, operating with a metal wall and helium exhaust. On DIII-D, limited experiments with high-βP plasmas operating with a divertor strike point on a (temporary) ring of tungsten tiles have shown promising results, with no significant degradation of core performance. However, to fully address the compatibility with a metal wall, we are collaborating closely with the Experimental Advanced Superconducting Tokamak (EAST) and Korea Superconducting Tokamak Advanced Research programme in the development of high-βP scenarios so that we can exploit their metal wall and long-pulse operation capabilities. Long-pulse operation (over 10 s) will further address the alignment for steady-state q-profiles and pressure profiles with ITB in the high-βP scenario. With regard to the helium exhaust, several review papers give favourable conclusions for high-βP plasmas with ITBs in JT-60U46,47. The results for JT-60U high-βP ITB plasmas show that the helium density in the core was controlled well and that no helium accumulation was observed, even with helium NBI for the core helium source. Moreover, the results also emphasize the importance of helium exhaust techniques, such as pumping, for controlling the helium content in the core.
Furthermore, there has been recent activity on extending the high-βP scenario towards true long-pulse operation, including modelling work for EAST48, ITER49,50 and FPPs under design10. Depending on the design philosophy of each group, the high-βP scenario can be applied in a wide range of FPP designs, from large conventional tokamaks14 to relatively small and compact devices9,10. One example from CAT-DEMO (Case D)9 shows a possible design point of an FPP using the high-βP scenario: R = 4 m, R/a = 3.1, BT = 7 T, Ip = 8.1 MA, q95 = 6.5, fGr = 1.3, fGr,ped = 1.0, βN = 3.6, H98y2 = 1.51, fusion gain Q = 17.3 and output electric power 200 MWe. The experimental achievement and the increased understanding reported in this paper may open a potential avenue to an operating point for producing economically attractive fusion energy.
Methods
DIII-D tokamak
The DIII-D National Fusion Facility51 is a tokamak research device operated by General Atomic in San Diego, California, for the US Department of Energy. DIII-D is the largest magnetic fusion research facility in the USA. The DIII-D programme is focused on establishing the scientific basis for the optimization of the tokamak approach to fusion energy production, in part through the development of advanced steady-state operating scenarios. The major and minor radii of DIII-D are 1.66 and 0.67 m, respectively. The toroidal field is up to 2.2 T at the magnetic axis, and the plasma current is up to 2 MA. DIII-D has four high-power NBI systems with a total power of up to 20 MW. Unique features of the DIII-D NBI systems include: (1) two horizontally rotatable beamlines, providing a capability for switching the off-magnetic axis neutral beam current drive from the co plasma-current direction to the counter plasma-current direction and (2) two vertically movable beamlines that enable the selection of on- or off-magnetic axis plasma heating and current drive in the experiment. DIII-D has six operational gyrotrons for heating the electron cyclotron and driving the current in the plasma. Each gyrotron is designed for 1 MW continuous-wave operation for several seconds at a central frequency of 110 GHz. Steerable antennas offer flexible heating and current drive methods in the plasma, including mid-plane launchers and top launchers. DIII-D is also developing a helicon system and a lower-hybrid wave system for additional radio-frequency heating and current drive capabilities. The extensive diagnostic set and the sophisticated plasma control system support various plasma experiments on DIII-D.
DIII-D high-β P experiments
Many international tokamaks have investigated high-βP scenarios34,35,52,53,54,55,56,57 ever since these scenarios were first proposed14 in 1990. High-βP experiments were explored by DIII-D58 in the 2000s and have been extensively investigated since 2013 by the joint DIII-D/EAST research team15. An ITB at large minor radius is the signature of the high-βP scenario in DIII-D. The latest physical understanding for developing such an ITB is through the reduced magnetic shear and sufficient α-stabilization effect40,59 (magnitude of αMHD). As αMHD ∝ q2 ∝ Ip−2, a relatively low plasma current and a broader current-density profile (having a higher q value and reduced magnetic shear at large radius) are beneficial for realizing ITB. DIII-D high-βP experiments usually begin with a lower Ip flat top, aiming at q95 ≈ 10 in the first phase of the discharge. An Ip ramp-up or BT ramp-down can be used in the later phase of the discharge to reduce the experimental q95 to a desired level, for example, 6–8. Edge perturbations, such as ELMs, active gas puffing and impurity injection have experimentally been found to trigger the formation of an ITB by creating a ‘low-(magnetic) shear detour’ at large radius, which gives access to the second stability regime. Experimentally, it has been found that an empirical βP threshold of between 1.7 and 1.9 in DIII-D can sustain a strong ITB at large radius15. Regarding the plasma shape and configuration, a double-null configuration and an inverted ITER-similar true single-null shape have been successfully tested in experiments. Despite the high qmin (over 2) in experiments, the high-βP scenario exhibits good fast-ion confinement, which is usually found to be classical. The present understanding60,61 indicates that: (1) The high-βP plasmas have a shorter slowing-down time (because of the high density) and lower ∇βfast, where βfast is the ratio of volume-averaged fast-ion pressure to the pressure of the toroidal magnetic field, which reduces the drive for Alfvénic modes. (2) The reverse-shear Alfvén eigenmodes are weaker or stable because the negative magnetic shear region is at higher radius, away from the peak of the fast-ion profile. Additionally, independent modelling of a high qmin (over 2) ITER 8 MA steady-state scenario (not the high-βP scenario) found that there was negligible fast-ion loss because of a mismatch between the loss boundaries and the locations of the Alfvén eigenmodes62. A more detailed description of experimental waveform designs and a comprehensive review of the high-βP scenario development on DIII-D in the last decade can be found in a review paper15.
Diagnostics for profiles
A multi-pulsed high-resolution Thomson scattering system63,64 was used to measure the core electron density and temperature in the DIII-D experiments. The ion temperature and the carbon density profiles were measured by a charge-exchange recombination spectroscopy system for C6+ particles65. The measurements were arranged radially on the low-field side.
Statistical analysis
Our statistical analysis used experimental data from DIII-D discharges during 2019–2022. We recorded data pairs of (fGr, H98y2) from two time slices for each discharge: (1) the highest H98y2 and the corresponding fGr at the same time and (2) the highest fGr and the corresponding H98y2 at the same time, unless the two time slices were the same. Several filters were applied: Ip ≥ 0.55 MA, dIp/dt < 0.5 MA s−1, Ptot ≥ 5 MW, W ≥ 500 kJ and (dW/dt)/Ptot ≤ 0.1. Here, W is the total energy stored by the plasma and Ptot is the total heating power. A smoothing window of 40 ms was applied. The minimum and maximum H98y2 values were truncated at 0.5 and 2.5, respectively. More than 3,600 discharges from 2019–2022 were used in the analysis.
Reconstruction of the kinetic equilibria
A multi-step workflow was used to add constraints on the pressure and plasma-current density in the equilibrium reconstruction to improve the accuracy of the reconstructed equilibrium. The workflow (for one iteration) has three parts: fitting the profile based on the existing equilibrium, calculating the power balance for the total pressure and plasma-current components, and reconstructing the equilibrium with pressure and current-density constraints. Usually, two or three iterations would be sufficient to produce high-quality equilibria for the transport study. When performing power balance calculation, NUBEAM66 was used for the NBI-driven current and fast-ion pressure calculation, and the Sauter model67 was used for the bootstrap current calculation. ONETWO68 was used to create the total pressure by combining the thermal pressure and fast-ion pressure and to provide the total plasma-current density by considering the external driven current, the bootstrap current and the calculated Ohmic current and by solving the poloidal field diffusion. The equilibrium was reconstructed with the EFIT code69.
Gyro-fluid transport modelling
The TGLF code38 was used to calculate the turbulent heat fluxes in the high-βP case and the low-q95 H-mode case. This modelling used a more recent saturation rule, SAT2 (ref. 70). Electromagnetic effects were included. The modelling took an experimental kinetic equilibrium from one time slice and focused on one radial location, for example, ρ = 0.65. The turbulent heat fluxes were predicted based on the local parameters of the selected time and radial location by taking contributions from several turbulent modes (low k and high k) into account. Quasi-neutrality was maintained when scanning the local density gradient Fp, meaning that the density gradients for all species changed accordingly. When scanning the local q, other quantities that are not independent of q were scanned accordingly. When scanning βe, the entire plasma β was changed accordingly, as Ti/Te and ni/ne were fixed in the modelling.
Pedestal modelling
The ELITE code41 was used to calculate the growth rate of the peeling–ballooning mode instability, which is believed to limit the achievable pedestal height by triggering ELMs when the plasma crosses the instability boundary. ELITE uses reconstructed equilibria with pressure and current constraints (kinetic equilibria) as input. On the basis of the input, a set of equilibria were generated by independently varying the edge pressure and current in a separate ELITE calculation to obtain the peeling–ballooning boundary.
The reduced three-field fluid module under the BOUT++ framework42,43,44 was used to simulate the edge modes. The simulation evolved several physics parameters: perturbed pressure, magnetic flux and vorticity. The three-field module included not only basic peeling–ballooning physics but also non-ideal effects, such as ion diamagnetic drift, E × B drift, resistivity and so on. The simulation domain in the normalized poloidal flux was 0.80 < ψN < 1.05 and the grid resolution was nψ = 512 and ny = 64. The kinetic equilibria were used as input. The Spitzer–Härm resistivity ηSp was used by considering realistic plasma kinetic profiles. The hyper-resistivity was taken as a constant value ηH = 10−16 in the generalized Ohm’s law for current diffusion. The radial electric field (Er) profile calculated from the ion momentum balance equation was used in the simulation.
Data availability
Raw data were generated by the DIII-D team. The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The computational codes used in the analysis of this paper are managed by General Atomics. They are available from the corresponding author upon reasonable request.
Change history
22 May 2024
A Correction to this paper has been published: https://doi.org/10.1038/s41586-024-07545-3
References
Conn, R. W. et al. Economic, safety and environmental prospects of fusion reactors. Nucl. Fusion 30, 1919 (1990).
Fasoli, A. Essay: overcoming the obstacles to a magnetic fusion power plant. Phys. Rev. Lett. 130, 220001 (2023).
Yeom, J. H. et al. System analysis study for Korean fusion DEMO reactor. Fusion Eng. Des. 88, 742 (2013).
Zhuang, G. et al. Progress of the CFETR design. Nucl. Fusion 59, 112010 (2019).
Lux, H. et al. Uncertainties in power plant design point evaluations. Fusion Eng. Des. 123, 63 (2017).
Federici, G. et al. DEMO design activity in Europe: progress and updates. Fusion Eng. Des. 136, 729 (2018).
Kessel, C. E. et al. The ARIES advanced and conservative tokamak power plant study. Fusion Sci. Technol. 67, 1 (2015).
Wade, M. R. & Leuer, J. A. Cost drivers for a tokamak-based compact pilot plant. Fusion Sci. Technol. 77, 119 (2021).
Buttery, R. J. et al. The advanced tokamak path to a compact net electric fusion pilot plant. Nucl. Fusion 61, 046028 (2021).
Shi, N. et al. Exploring high performance scenarios for a fusion pilot plant by integrated modeling. In 64th Annual Meeting of the APS Division of Plasma Physics, Vol. 67, UP11.00004 (APS, 2022).
Greenwald, M. et al. A new look at density limits in tokamaks. Nucl. Fusion 28, 219 (1988).
Christiansen, J. P. et al. Global energy confinement H-mode database for ITER. Nucl. Fusion 32, 291 (1992).
Wagner, F. et al. Regime of improved confinement and high beta in neutral-beam-heated divertor discharges of the ASDEX tokamak. Phys. Rev. Lett. 49, 1408 (1982).
Kikuchi, M. Steady state tokamak reactor based on the bootstrap current. Nucl. Fusion 30, 265 (1990).
Ding, S. & Garofalo, A. M. Progress in the development and understanding of a high poloidal-beta tokamak operating scenario for an attractive fusion pilot plant. Rev. Mod. Plasma Phys. 7, 4 (2023).
Ongena, J. & Van Oost, G. Energy for future centuries: prospects for fusion power as a future energy source. Fusion Sci. Technol. 61, 3 (2012).
Taylor, T. S. Physics of advanced tokamaks. Plasma Phys. Control. Fusion 39, B47 (1997).
Kikuchi, M. & Azumi, M. Steady-state tokamak research: core physics. Rev. Mod. Phys. 84, 1807 (2012).
Wesson, J. Tokamaks 3rd edn, Ch. 1, 4–9 (Oxford Univ. Press, 2004).
Doyle, E. J. et al. Chapter 2: Plasma confinement and transport. Nucl. Fusion 47, S18 (2007).
Kamada, Y., Hosogane, N., Yoshino, R., Hirayama, T. & Tsunematsu, T. Study of the density limit with pellet fuelling in JT-60. Nucl. Fusion 31, 1827 (1991).
Greenwald, M. Density limits in toroidal plasmas. Plasma Phys. Control. Fusion 44, R27 (2002).
Angioni, C. et al. Particle transport in tokamak plasmas, theory and experiment. Plasma Phys. Control. Fusion 51, 124017 (2009).
Osborne, T. H. et al. Gas puff fueled H-mode discharges with good energy confinement above the Greenwald density limit on DIII-D. Phys. Plasmas 8, 2017 (2001).
Lang, P. T. et al. High-density H-mode operation by pellet injection and ELM mitigation with the new active in-vessel saddle coils in ASDEX Upgrade. Nucl. Fusion 52, 023017 (2012).
Lang, P. T. et al. ELM pacing and high-density operation using pellet injection in the ASDEX Upgrade all-metal-wall tokamak. Nucl. Fusion 54, 083009 (2014).
Pitts, R. A. et al. Physics basis for the first ITER tungsten divertor. Nucl. Mater. Energy 20, 100696 (2019).
Eich, T. et al. ELM divertor peak energy fluence scaling to ITER with data from JET, MAST and ASDEX upgrade. Nucl. Mater. Energy 12, 84 (2017).
Xu, G. S. et al. Recent advances in developing natural and impurity-induced small/no-ELM H-mode regimes in EAST. Rev. Mod. Plasma Phys 7, 14 (2023).
Kamada, Y. et al. Disappearance of giant ELMs and appearance of minute grassy ELMs in JT-60U high-triangularity discharges. Plasma Phys. Control. Fusion 42, A247 (2000).
Burrell, K. H. et al. Advances in understanding quiescent H-mode plasmas in DIII-D. Phys. Plasmas 12, 056121 (2005).
Evans, T. E. et al. Edge stability and transport control with resonant magnetic perturbations in collisionless tokamak plasmas. Nat. Phys. 2, 419 (2006).
Liang, Y. et al. Magnetic topology changes induced by lower hybrid waves and their profound effect on edge-localized modes in the EAST tokamak. Phys. Rev. Lett. 110, 235002 (2013).
Koide, Y. et al. Internal transport barrier on q = 3 surface and poloidal plasma spin up in JT-60U high-βP discharges. Phys. Rev. Lett. 72, 3662 (1994).
Sakamoto, Y. et al. Stationary high confinement plasmas with large bootstrap current fraction in JT-60U. Nucl. Fusion 45, 574 (2005).
Garofalo, A. M. et al. Compatibility of internal transport barrier with steady-state operation in the high bootstrap fraction regime on DIII-D. Nucl. Fusion 55, 123025 (2015).
Wang, L. et al. Integration of full divertor detachment with improved core confinement for tokamak fusion plasmas. Nat. Commun. 12, 1365 (2021).
Staebler, G. M., Kinsey, J. E. & Waltz, R. E. Gyro-Landau fluid equations for trapped and passing particles. Phys. Plasmas 12, 102508 (2005).
Kotschenreuther, M. T. et al. Regimes of weak ITG/TEM modes for transport barriers without velocity shear. In 61st Annual Meeting of the APS Division of Plasma Physics, Vol. 64, UP10.00020 (APS, 2019).
Ding, S. et al. Confinement improvement in the high poloidal beta regime on DIII-D and application to steady-state H-mode on EAST. Phys. Plasmas 24, 056114 (2017).
Snyder, P. B. et al. Edge localized modes and the pedestal: a model based on coupled peeling–ballooning modes. Phys. Plasmas 9, 2037 (2002).
Dudson, B. D., Umansky, M. V., Xu, X. Q., Snyder, P. B. & Wilson, H. R. BOUT++: a framework for parallel plasma fluid simulations. Comput. Phys. Commun. 180, 1467 (2009).
Xu, X. Q., Dudson, B. D., Snyder, P. B., Umansky, M. V. & Wilson, H. R. Nonlinear simulations of peeling–ballooning modes with anomalous electron viscosity and their role in edge localized mode crashes. Phys. Rev. Lett. 105, 175005 (2010).
Li, Z.-Y. et al. Ideal MHD stability and characteristics of edge localized modes on CFETR. Nucl. Fusion 58, 016018 (2018).
Soukhanovskii, V. A. A review of radiative detachment studies in tokamak advanced magnetic divertor configurations. Plasma Phys. Control. Fusion 59, 064005 (2017).
Hogan, J. Helium transport and exhaust experiments in tokamaks. J. Nucl. Mater. 241, 68 (1997).
Litaudon, X. Internal transport barriers: critical physics issues? Plasma Phys. Control. Fusion 48, A1 (2006).
Ding, S., Jian, X., Garofalo, A. M. & Wang, H. Strategy for developing internal transport barriers at large radius in high poloidal beta plasmas on EAST. In 63rd Annual Meeting of the APS Division of Plasma Physics, Vol. 66, CP11.00012 (APS, 2021).
McClenaghan, J. et al. Transport at high βP and development of candidate steady state scenarios for ITER. Nucl. Fusion 60, 046025 (2020).
Ding, S. et al. A low plasma current (~8 MA) approach for ITER’s Q = 10 goal. In Proc. 28th IAEA Fusion Energy Conference (IAEA, 2021).
Luxon, J. L. A brief introduction to the DIII-D tokamak. Fusion Sci. Technol. 48, 828 (2005).
Sabbagh, S. A. et al. High poloidal beta equilibria in the Tokamak Fusion Test Reactor limited by a natural inboard poloidal field null. Phys. Fluids B 3, 2277 (1991).
Hobirk, J. et al. Reaching high poloidal beta at Greenwald density with internal transport barrier close to full noninductive current drive. Phys. Rev. Lett. 87, 085002 (2001).
Litaudon, X. et al. Towards fully non-inductive current drive operation in JET. Plasma Phys. Control. Fusion 44, 1057 (2002).
Garofalo, A. M. et al. Development of high poloidal beta, steady-state scenario with ITER-like tungsten divertor on EAST. Nucl. Fusion 57, 076037 (2017).
Park, H. K. et al. Overview of KSTAR research progress and future plans toward ITER and K-DEMO. Nucl. Fusion 59, 112020 (2019).
Chen, W. et al. High-βP scenario realized by the integration of internal and external transport barriers in the HL-2A tokamak. Phys. Lett. A 440, 128141 (2022).
Politzer, P. A. et al. Stationary, high bootstrap fraction plasmas in DIII-D without inductive current control. Nucl. Fusion 45, 417 (2005).
Staebler, G. M. et al. Transport barriers in bootstrap-driven tokamaks. Phys. Plasmas 25, 056113 (2018).
Holcomb, C. T. et al. Fast-ion transport in qmin > 2, high-β steady-state scenarios on DIII-D. Phys. Plasmas 22, 055904 (2015).
Huang, J. et al. Progress in extending high poloidal beta scenarios on DIII-D towards a steady-state fusion reactor and impact of energetic particles. Nucl. Fusion 60, 126007 (2020).
Van Zeeland, M. A. et al. Alfvén eigenmode stability and fast ion loss in DIII-D and ITER reversed magnetic shear plasmas. Nucl. Fusion 52, 094023 (2012).
Carlstrom, T. N. et al. Design and operation of the multipulse Thomson scattering diagnostic on Dill-D (invited). Rev. Sci. Instrum. 63, 4901 (1992).
Eldon, D. et al. Initial results of the high resolution edge Thomson scattering upgrade at DIII-D. Rev. Sci. Instrum. 83, 10E343 (2012).
Seraydarian, R. P. & Burrell, K. H. Multichordal charge exchange recombination spectroscopy on the DIII-D tokamak. Rev. Sci. Instrum. 57, 2012 (1986).
Pankin, A., McCune, D., Andre, R., Bateman, G. & Kritz, A. The tokamak Monte Carlo fast ion module NUBEAM in the National Transport Code Collaboration library. Comput. Phys. Commun. 159, 157 (2004).
Sauter, O., Angioni, C. & Lin-Liu, Y. R. Neoclassical conductivity and bootstrap current formulas for general axisymmetric equilibria and arbitrary collisionality regime. Phys. Plasmas 6, 2834 (1999).
St. John, H., Taylor, T., Lin-Liu, Y. R. & Turnbull, A. D. Transport Simulation of Negative Magnetic Shear Discharges (US Department of Energy Office of Scientific and Technical Information, 1994).
Lao, L. L., St. John, H., Stambaugh, R. D., Kellman, A. G. & Pfeiffer, W. Reconstruction of current profile parameters and plasma shapes in tokamaks. Nucl. Fusion 25, 1611 (1985).
Staebler, G. M. et al. Verification of a quasi-linear model for gyrokinetic turbulent transport. Nucl. Fusion 61, 116007 (2021).
Acknowledgements
We thank the DIII-D team and the joint DIII-D/EAST research team for their support in the machine operation and data analysis and modelling. We express our deep gratitude to E. J. Strait of General Atomics for his suggestions on improving the manuscript text. Additionally, we thank M. T. Kotschenreuther of ExoFusion for insightful discussions on transport physics, which contributed significantly to the development of this work. This work is supported by the US Department of Energy (Grant Nos. DE-SC0010685, DE-FC02-04ER54698, DE-AC52-07NA27344, DE-FG02-04ER54761, DE-AC02-09CH11466 and DE-SC0016154). This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.
Author information
Authors and Affiliations
Contributions
S.D. and A.M.G. conceived the experimental idea regarding DIII-D. S.D. led the experimental demonstration and conducted the DIII-D database analysis, equilibrium reconstructions, gyro-fluid transport modelling and writing the manuscript. A.M.G. provided guidance during the writing of the manuscript. H.Q.W. performed the pedestal stability and divertor condition analysis and provided the target low-q95 discharge for analysis. Z.Y.L. performed the pedestal modelling. S.D., A.M.G., H.Q.W., X.J., L.W., X.Z.G., J.P.Q., J.H., J.M. and C.T.H. participated in designing and executing the experiments. D.B.W., D.E., B.S.V., A.M., Q.M.H., I.S.C., T.O., A.W.H., T.H.O. and J.M.H. participated in executing the experiments. T.O. conducted the impurity analysis. All authors reviewed the manuscript. A.M.G. and C.T.H. polished the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Xavier Litaudon and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
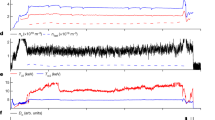
Extended Data Fig. 1 Additional time histories for DIII-D # 190904.
(a) Plasma current in blue and toroidal field in green; (b) Line-averaged density in blue and stored energy in green; (c) On-axis electron density in blue, on-axis deuterium density in green and on-axis carbon density in violet; (d) Measured neutron rate; (e) Injected NBI power in blue, measured total radiated power in green and core radiated power in violet.
Extended Data Fig. 2 Additional profiles for DIII-D # 190904.
Deuterium density profiles in (a), ratio between carbon density and electron density in (b) and safety factor profiles (q-profiles) in (c). Different color indicates the time slice shown in Fig. 2a. Additionally, profiles for a pre-ITB time slice (1.89 s) shown in gray dashed line are added.
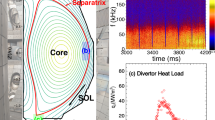
Extended Data Fig. 3 Spatial and temporal evolution of electron temperature at the divertor plates, measured by Langmuir probes.
ψN is normalized poloidal flux. ψN < 1.0 locates within the private flux region. Color coding shows the measured Te,div. Dashed lines indicate the actual positions of Langmuir probes.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ding, S., Garofalo, A.M., Wang, H.Q. et al. A high-density and high-confinement tokamak plasma regime for fusion energy. Nature 629, 555–560 (2024). https://doi.org/10.1038/s41586-024-07313-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-024-07313-3
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.