Abstract
A viscosity jump of one to two orders of magnitude in the lower mantle of Earth at 800–1,200-km depth is inferred from geoid inversions and slab-subducting speeds. This jump is known as the mid-mantle viscosity jump1,2. The mid-mantle viscosity jump is a key component of lower-mantle dynamics and evolution because it decelerates slab subduction3, accelerates plume ascent4 and inhibits chemical mixing5. However, because phase transitions of the main lower-mantle minerals do not occur at this depth, the origin of the viscosity jump remains unknown. Here we show that bridgmanite-enriched rocks in the deep lower mantle have a grain size that is more than one order of magnitude larger and a viscosity that is at least one order of magnitude higher than those of the overlying pyrolitic rocks. This contrast is sufficient to explain the mid-mantle viscosity jump1,2. The rapid growth in bridgmanite-enriched rocks at the early stage of the history of Earth and the resulting high viscosity account for their preservation against mantle convection5,6,7. The high Mg:Si ratio of the upper mantle relative to chondrites8, the anomalous 142Nd:144Nd, 182W:184W and 3He:4He isotopic ratios in hot-spot magmas9,10, the plume deflection4 and slab stagnation in the mid-mantle3 as well as the sparse observations of seismic anisotropy11,12 can be explained by the long-term preservation of bridgmanite-enriched rocks in the deep lower mantle as promoted by their fast grain growth.
Similar content being viewed by others
Main
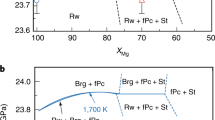
The lower mantle of Earth consists of bridgmanite as the most abundant mineral phase, followed by ferropericlase and davemaoite as the second and third phases, respectively. Silicate melting and solidification experiments13,14 demonstrate that bridgmanite is the first phase to crystallize from a magma ocean in the early stages of the history of Earth. Owing to fractional crystallization15, bridgmanite-enriched rocks with low ferropericlase proportion (Xfpc <5–10%) were formed at more than about 1,000-km depth, evolving into pyrolitic (or peridotitic) rocks with relatively high Xfpc (≈20%) at shallower depths, whereas the davemaoite content is lower than that of ferropericlase or even absent in the deep lower mantle16. The bridgmanite-enriched rocks could be preserved until the present day without mixing by mantle convection5,6,7,17 as demonstrated by the current mantle seismic and density profiles, both of which agree well with pyrolitic compositions in the shallow lower mantle and bridgmanite-enriched rocks in the deeper regions18,19,20,21. A bridgmanite-enriched deep lower mantle is also supported by the density crossover between bridgmanite and ferropericlase—that is, bridgmanite-enriched rocks are denser than pyrolitic rocks in the mid-mantle20.
It was previously considered that bridgmanite is rheologically stronger than ferropericlase22,23,24. Thus, bridgmanite-enriched rocks may have a higher viscosity than those of pyrolitic rocks, which may lead to an increase in viscosity with depth. The increase in strength of ferropericlase with pressure23,25 and the iron spin transition26 may also cause an increase in viscosity. However, using these scenarios to explain an increase in viscosity of one to two orders of magnitude requires an interconnected framework of ferropericlase (ferropericlase-controlled lower mantle rheology)5,22, which is unlikely because the electrical conductivity of the lower mantle is comparable to that of bridgmanite27,28, but three orders of magnitude smaller than that of ferropericlase27. In particular, recent atomic modelling29 shows periclase has a slower creep rate than that of bridgmanite under mantle conditions, whereas deformation experiments30 suggest that bridgmanite has an identical creep rate to that of post-spinel (70% bridgmanite + 30% ferropericlase); both of these findings indicate a bridgmanite-controlled lower-mantle rheology. Moreover, the oxygen vacancies in bridgmanite formed by the substitutions of Si4+ with Al3+ and Fe3+ have been proposed to cause an increase in bridgmanite strength with depth31,32,33. However, Al3+ and Fe3+ are more likely to form FeAlO3 in bridgmanite34. Furthermore, the contribution of davemaoite to lower-mantle rheology should be limited as well because of its low volume fraction (and thus no interconnection)16, although davemaoite is rheologically weaker than bridgmanite35.
Because the viscosity (η) of polycrystalline aggregates has a strong grain-size (d) dependence (η ∝ d2 ~ d3) in the diffusion creep regime, which may play an essential part in lower-mantle rheology11, constraints on grain size and grain-growth rate of bridgmanite are crucial for understanding the viscosity of the lower mantle36. However, the grain size and grain-growth rate have so far only been experimentally investigated at a fixed Xfpc of 30% (refs. 37,38). As the lower mantle consists of both pyrolitic rocks with high Xfpc and bridgmanite-enriched rocks with low Xfpc as discussed above5,6,7,17,18,19, the influence of the proportion of ferropericlase on bridgmanite growth rate needs to be investigated.
Here we investigated the grain-growth kinetics of bridgmanite as a function of Xfpc by multi-anvil high-pressure experiments. Aggregates of bridgmanite with different Xfpc (about 0–60%) were pre-synthesized from San Carlos olivine, orthopyroxene (opx), solution–gelation-derived silicates (sol–gel) and melt-quenched silicate glasses (Extended Data Table 1) and annealed at 27 GPa and 2,200 K for 1.5–1,000 min for grain growth (Extended Data Table 2). The grain sizes were obtained from backscattered electron images of the recovered samples (Fig. 1), from which the growth-rate constant was calculated. Details of the experiment are provided in the Methods.
a–d, Backscattered electron images (dark, bridgmanite; bright, ferropericlase) and grain-size distribution. n, number of analysed grains; \(\bar{d}\), average grain size obtained from mean log(d), which decreases with increase in Xfpc. Scale bars, 10 μm (a), 5 μm (b) and 2 μm (c and d).
Evolution of grain size over time
The recovered samples show that the grain-size distribution in log units (log(d)) follows a Gaussian distribution (Fig. 1). As expected, the mean grain size increases with an increase in annealing duration for both single-phase (Xfpc = 0%) and two-phase aggregates (Fig. 2). After annealing at 2,200 K for 1.5–1,000 min, the grain size of samples with Xfpc = 0% is 0.7–1.0 orders of magnitude larger than those with Xfpc = 30% (Fig. 2). Samples pre-synthesized from different starting materials (olivine, opx, sol–gel and glasses) show consistent results (Fig. 3a–c).
After annealing at 27 GPa and 2,200 K, for the indicated annealing time, the grain size of bridgmanite in the single-phase system (Xfpc = 0%, from opx) is significantly larger than the aggregates with 30% of ferropericlase (Xfpc = 30%, from olivine). The grain-size exponent n is smaller when Xfpc = 0%, indicating faster grain-size evolution over time.
a–c, Grain sizes after annealing at 27 GPa, 2,200 K for 100 min (a), 10 min (b) and 1.5 min (c). Samples synthesized from different starting materials (olivine, opx, sol–gel and glasses) show consistent results. d, Grain-size exponent n. e, Growth-rate constant k. The solid line in d is obtained by assuming that n increases continuously with an increase in Xfpc following the empirical equation \(n={A}^{{\prime} }\exp \left({X}_{{\rm{fpc}}}/{B}^{{\prime} }\right)+{C}^{{\prime} }\), whereas the dashed line represents a discontinuous change of n with Xfpc—that is, n = 2.9 at Xfpc < 3% and n = 5.2 at Xfpc > 3%. Accordingly, the solid and dashed lines in e are fitting curves of k to the equation \(\log (k)={A}^{{\prime\prime} }\exp \left({X}_{{\rm{fpc}}}/{B}^{{\prime\prime} }\right)+{C}^{{\prime\prime} }\)(k in units of μmn s−1) based on the continuous and discontinuous n, respectively. The fitting parameters are shown in the figure. The solid and dashed lines in a–c are calculated from the n–Xfpc and k–Xfpc relations in d and e.
Grain growth of polycrystalline aggregates follows a power law that can be approximated by
where d denotes grain size after a growth experiment of duration t, d0 is the initial grain size, k is the growth-rate constant and n is the grain-size exponent (coarsening exponent). For our annealing durations, d exceeds d0 by more than a factor of three (Extended Data Fig. 1); therefore, d0 can be neglected in equation (1). Hence, log(d) increases approximately linearly with increasing log(t) (Fig. 2). The slopes of the fitting lines represent 1/n in equation (1).
Least-squares fitting of our data yields n = 2.9 ± 0.2 and 5.2 ± 0.3 for Xfpc = 0% and 30%, respectively37 (Fig. 2). These two values of n agree well with those obtained from theoretical models—that is, n = 2–3 for grain growth controlled by grain-boundary diffusion in a single-phase system and n = 4–5 for a two-phase system39,40, and are comparable to those reported for other minerals such as olivine, wadsleyite and ringwoodite (single phase)41,42,43 as well as olivine–pyroxene and forsterite–nickel aggregates (two phases)44,45. For intermediate Xfpc, the grain size also increases with increasing duration (Fig. 3a–c). However, n ranges from 3.1 to 6.2 because of the scatter of data points (Fig. 3d).
Effects of X fpc on the rate of grain growth
The growth rate of bridgmanite is found to be significantly reduced by the presence of ferropericlase. After annealing for 1.5–100 min, the grain size of samples with Xfpc ≈ 10% is smaller by 0.5–0.8 orders of magnitude than for Xfpc = 0%, but at higher Xfpc (up to about 60%) the ferropericlase proportion has a minor effect (Fig. 3a–c). This decrease in grain size with increasing Xfpc cannot be ascribed to differences in Fe content for two reasons. First, our samples did not show a large variation in Fe contents (Extended Data Table 3). Second, bridgmanite synthesized from olivine (Fe/(Mg + Fe) ≈ 10%) and from Fe-free forsterite show only a difference in grain size of 0.1 log units37.
As shown above, although the exponents n for Xfpc = 0% and 30% are well constrained (Fig. 2), the n–Xfpc relation is unknown because of the scatter of data points for intermediate Xfpc (Fig. 3d). The exponent n may change with Xfpc either continuously or discontinuously. We therefore fit the data points to both continuous and discontinuous n–Xfpc models in Fig. 3d. In either case, the growth-rate constant k = dn/t (k in units of μmn s−1) decreases with increasing Xfpc. The fitting curves of k–Xfpc based on the two n–Xfpc models are essentially the same (Fig. 3e).
Grain growth in a two-phase system is controlled by growth of the matrix (bridgmanite) and coarsening of the second phase (ferropericlase) by Ostwald ripening. If ferropericlase coarsening does not occur, the grain size of bridgmanite should be limited by a constant value of the interparticle spacing of ferropericlase (\(\bar{r}\), the average distance between adjacent ferropericlase grains). To understand whether ferropericlase coarsening occurs or not, the changes in \(\bar{r}\) and dfpc (grain size of ferropericlase) over time are examined. It is found that dfpc increases with time in both low-Xfpc (approximately 3–3.5%) and high-Xfpc (approximately 18.5%) samples with similar rates as bridgmanite, whereas \(\bar{r}\) increases with time systematically and is linearly proportional to the grain size of bridgmanite (Extended Data Figs. 2 and 3). Therefore, both dfpc and \(\bar{r}\) indicate simultaneous ferropericlase coarsening and bridgmanite growth. The growth rate of bridgmanite is affected by ferropericlase even at low Xfpc (for example, about 3%) (Fig. 3), which is characteristic of two-phase systems in general44,46.
Variation in viscosity with X fpc
Our experimental results indicate that the grain growth rate of bridgmanite-enriched rocks should be much faster (two to three orders of magnitude larger in k as shown in Fig. 3d) than that of pyrolitic rocks. The growth-rate contrast should readily cause a grain-size contrast and this grain-size contrast increases further with geological time (Fig. 2). Over a short timescale of 10 Myr (that is, shortly after magma ocean crystallization) at a temperature of 2,200 K (typical mid-mantle temperatures47), the grain size of bridgmanite-enriched rocks already exceeds that of pyrolitic rocks by about two orders of magnitude. Over a timescale of 4.5 Gyr (that is, the whole history of Earth), the grain-size difference reaches around 2.5 orders of magnitude (Fig. 4a).
a, Grain size of bridgmanite calculated for growth over geological timescales of 10 Myr to 4.5 Gyr at 2,200 K. b, Simulated creep rates at 2,200 K assuming a stress of 0.5 MPa and grain size after growth for 4.5 Gyr. c, Relative viscosity at 2,200 K at stresses of 0.1–1 MPa (where σ denotes stress) and grain size after 4.5 Gyr. d, Variation in grain size with depth along a lower-mantle geotherm47 after 4.5 Gyr by assuming Xfpc = 5% in bridgmanite-enriched rocks and Xfpc = 20% in pyrolitic rocks. e, Comparison of relative viscosity based on geophysical observations1 (thick grey curve) and calculations with grain size from d at a stress of 1.0 MPa (red curves) and 0.5 MPa (blue curves). The solid and dashed lines represent calculations based on the continuous and discontinuous variations in n with Xfpc given in Fig. 3d, respectively. Note that the viscosity profiles in the figure represent only the relative changes with depth.
To infer the viscosity contrast of rocks with variable Xfpc, the diffusion- and dislocation-creep rates are calculated as a function of Xfpc based on the growth rate of bridgmanite determined in this study and the Si diffusivity determined in previous studies given in Extended Data Table 4 (for calculation details and uncertainty analysis, see Methods and Extended Data Figs. 4 and 5). Because of the inverse power relation, a grain-size contrast of two orders of magnitude causes the diffusion-creep rate of pyrolitic rocks that is more than four orders of magnitude higher than that of bridgmanite-enriched rocks (Fig. 4b). By contrast, the dislocation-creep rate is independent of grain size. As a result, the total creep rate of pyrolitic rocks remains one to two orders of magnitude higher (Fig. 4b) and, therefore, the viscosity is accordingly lower than that of bridgmanite-enriched rocks (Fig. 4c). Although the magnitude of the viscosity contrast depends on the stress conditions because of the contribution of dislocation creep (Fig. 4c), the non-hydrostatic stress in most of the mantle of Earth is estimated to be ≤1.0 MPa (ref. 48) or even ≤0.3 MPa (ref. 24). In this case, the grain-size contrast always causes a significant viscosity contrast even if dislocation creep dominates in the bridgmanite-enriched rocks (Fig. 4c and Methods).
Viscosity jump in the mid-mantle
Our results provide an explanation for the long-term preservation of bridgmanite-enriched rocks in the deep lower mantle as indicated by geophysical and geodynamical constraints5,6,7,18,19,20. Bridgmanite-enriched rocks formed in the deep lower mantle at the early stage of the history of Earth because of magma ocean crystallization13,14,15 are expected to have developed grain sizes that are more than two orders of magnitude larger, and therefore have a much higher viscosity, than the overlying pyrolitic rocks in around 100 Myr or less (Fig. 4a,c). The high viscosity of these early-developed bridgmanite-enriched rocks should prevent them from being mixed with pyrolitic rocks over the age of Earth, leading to their preservation over geological timescales5,6,7. By contrast, pyrolitic rocks are gravitationally stable at the topmost and bottom layers of the lower mantle20. Therefore, these rocks may circulate around the bridgmanite-enriched rocks through narrow and rheologically weak channels5,7.
The mid-mantle viscosity jump1 can thus be explained by the grain-size contrast between bridgmanite-enriched rocks and the overlying pyrolite. Along a typical geotherm47, the grain size of bridgmanite in each rock continuously increases with depth as temperature increases, and a grain-size increase of about one order of magnitude (based on the continuous n in Fig. 3d) occurs at 800–1,200-km depth owing to the transition from pyrolitic-to-bridgmanite-enriched rocks with depth (Fig. 4d). Accordingly, a viscosity increase by about one order of magnitude is sustained (for a stress of 1.0 MPa), which agrees with the geophysically constrained viscosity jump in the mid-mantle (Fig. 4e). For lower stresses, the viscosity increase would be even larger—that is, about 1.3 orders of magnitude for a stress of 0.5 MPa (Fig. 4e). Although the viscosity increase at 800–1,200-km depth is smaller using the discontinuous n model (Fig. 3d), it is still about one order of magnitude for a stress of about 0.5 MPa (Fig. 4e). Note that the experimental pressure conditions in this study were limited to 27 GPa, corresponding to a depth of 800 km. Considering a negative pressure dependence of grain growth43, the grain size as well as the viscosity of pyrolitic rocks decreases with depth. By contrast, the viscosity of bridgmanite-enriched rocks is independent of grain size because of the dominance of dislocation creep. Thus, the viscosity contrast between pyrolitic and bridgmanite-enriched rocks is expected to be even larger.
Our main finding that the grain-growth rate increases sharply with bridgmanite enrichment thus provides a unified explanation for the preservation of ancient bridgmanite-enriched rocks over geological timescales5,7 and the present-day viscosity jump in the mid-mantle1 (Fig. 4e). Although the grain-size increase with depth may not occur globally at 800–1,200-km depth, it should be sufficient to affect a wide range of geophysical and geochemical processes. For example, the sinking of slabs may be slowed down in the regions in which they encounter high-viscosity bridgmanite-enriched rocks, leading to slab stagnation at about 1,000-km depth as indicated by seismic observations3. The plumes ascend vertically through the bridgmanite-enriched deep lower mantle4, but they may be deflected at about 1,000-km depth because of the horizontal flow promoted in the pyrolitic rocks just above the viscosity jump as shown by full-waveform seismic tomography4. Furthermore, the bridgmanite-enriched rocks may sustain widespread seismic reflectors49, host primordial geochemical anomalies (for example, 142Nd, 182W and 3He) in the deep mantle9,10 and balance the discrepancy in Mg:Si ratio between upper-mantle rocks (Mg:Si ≈ 1.3) and the building blocks of Earth8 (chondrites, Mg:Si ≈ 1.05).
The lower-mantle rheological structure as predicted by our grain-size model may further explain the lack of observed seismic anisotropy. In the pyrolitic shallow lower mantle, diffusion creep dominates because of the small grain sizes (Fig. 4b), leading to the absence of seismic anisotropy11. In turn, because of the high viscosity, the bridgmanite-enriched deep lower mantle may accumulate little strain and thus no anisotropy owing to the high viscosity5,6,7, despite the dominance of dislocation creep (Fig. 4b). Anisotropy in the lower mantle is therefore restricted to regions with high stress and significantly accumulated strains such as near subducting slabs, leading to locally enhanced seismic anisotropy12.
Methods
Starting materials
Four types of starting material were used in this study: (1) olivine powder with a composition of (Mg,Fe)2SiO4; (2) opx powder with a composition of (Mg,Fe)SiO3; (3) sol–gel-derived silicate powders with bulk compositions of (Mg,Fe)1.5SiO3.5, (Mg,Fe)1.25SiO3.25 and (Mg,Fe)1.125SiO3.125; (4) silicate glass powders with bulk compositions of (Mg,Fe)xSiO2+x (x = 1.5, 1.4, 1.3, 1.2, 1.1, 1.05 and 1.02). The Mg:Fe atomic ratios in all of the powders were about 9:1.
Material 1 was prepared by grinding hand-picked single crystals of San Carlos olivine. Material 2 was prepared from MgO, FeO and SiO2 oxides. Both materials 1 and 2 were used in a previous study50. Material 3 was prepared from tetraethyl orthosilicate and metallic Mg and Fe dissolved in dilute nitric acid following the procedure reported in ref. 51. The powders have compositions between those of materials 1 and 2 to trace the grain-growth kinetics as a function of Xfpc. However, the products of material 3 after high-pressure synthesis were found to have inhomogeneous ferropericlase distributions as described in the section below (Extended Data Fig. 1). Therefore, the silicate glasses (material 4) were prepared by quenching the oxide melts with (Mg,Fe)xSiO2+x bulk compositions (x as described above) from about 2,500 K (estimated with an optical pyrometer) to room temperature in an aerodynamic levitator equipped with a two-CO2-laser heating system52. The products of material 4 after high-pressure synthesis have uniform ferropericlase distributions (Extended Data Fig. 1). The powders of materials 3 and 4 were annealed at 1,100 K for 24 h in an ambient-pressure CO–CO2 gas-mixing furnace with oxygen partial pressure controlled at approximately 0.5 log units above the iron–wüstite buffer to reduce the ferric iron to a ferrous state. All the powders were stored in a vacuum furnace at 400 K before use.
Synthesis of bridgmanite–ferropericlase aggregates
Bridgmanite with various fractions of ferropericlase was synthesized from the above-mentioned starting materials using a multi-anvil press. The detailed synthesis procedures have been described previously37. In brief, multiple layers of starting materials separated by Fe foils were loaded into Pt capsules with outer and inner diameters of 1.0 and 0.8 mm, respectively. The thickness of each layer was about 0.15 mm. Small amounts of Fe–FeO powder were loaded next to the Fe foils to buffer the oxygen fugacity. High-pressure experiments were performed by the multi-anvil technique using a Cr2O3-doped MgO octahedral pressure medium with a 7-mm edge length with a LaCrO3 furnace and tungsten carbide anvils with a 3-mm truncation edge length (7/3 assembly). The pressure and temperature conditions were 27 GPa and 1,700 K, respectively. The heating duration was 5 min. The run conditions and products are summarized in Extended Data Table 1.
Homogeneously distributed bridgmanite–ferropericlase mixtures with a grain size much less than 0.1 μm (post-spinel) and single-phase bridgmanite with a grain size of approximately 0.42 μm (opx–bridgmanite) were synthesized from materials 1 and 2, respectively (Extended Data Fig. 1a,b). The samples synthesized from material 3 have an inhomogeneous distribution (locally homogeneous) of bridgmanite and ferropericlase grains (Extended Data Fig. 1c), probably because of an inhomogeneous Si distribution during gelation. The grain size is approximately 0.15 μm. The samples synthesized from material 4 seemed to be homogenous, with a grain size of about 0.2 μm (Extended Data Fig. 1d).
Grain-growth experiments
All the synthesized aggregates were mechanically broken into small pieces (each 100–200 μm in size). Multiple pieces were embedded in pre-dried CsCl powder in Pt capsules, which provided quasi-hydrostatic conditions50,53. An Fe–FeO powder was loaded at the two ends of the Pt capsules to buffer the oxygen fugacity (\({f}_{{{\rm{O}}}_{2}}\)). The capsules were loaded into the 7/3 multi-anvil cell assemblies and compressed to 27 GPa, followed by heating at 2,200 K for 1.5–1,000 min (Extended Data Table 2). Because of the relatively fast heating and cooling speeds (2–3 min for heating from 1,700 to 2,200 K and less than 1 s for cooling from 2,200 K to below 1,700 K), the growth during heating and cooling is negligible.
Sample analysis
The recovered samples were separated from CsCl by dissolution in water, polished and observed using a scanning electron microscope with acceleration voltages of 5–20 kV. Bridgmanite and ferropericlase grains were distinguished by the brightness contrast in backscattered electron (BSE) images (Fig. 1). The volume fraction of ferropericlase was obtained from the BSE images. The area of each bridgmanite grain was determined using an image processing software (ImageJ). The grain size (d) of each grain was obtained from the diameter of the area-equivalent circle. The grain size in log units (log(d)) showed a Gaussian distribution (Fig. 1); therefore, the mean grain sizes (\(\bar{d}\)) were calculated from the mean log(d) based on the Gaussian distribution37.
The bridgmanite and ferropericlase grains were homogeneously distributed in the post-spinel, opx-bridgmanite and glass samples. More than 130 bridgmanite grains were analysed for each sample (Extended Data Table 2). In the sol–gel samples, BSE images were taken on locally homogenous areas. Each data point of the sol–gel samples (Fig. 3a) represents the grain size and Xfpc in an individual BSE image. As mentioned above, the heterogeneity had occurred during the sample synthesis procedure, after which the grains already reached an equilibrated texture (120° triple junction, Extended Data Fig. 1c). Therefore, the grain growth in each locally homogenous area during the annealing experiment should not be affected. This is confirmed by the consistent results obtained in the sol–gel, glass, opx-bridgmanite and post-spinel samples. Some metallic iron particles that locally appeared in the sol–gel samples (Supplementary Figs. 49–53) are also expected to have a negligible effect on the log(d)–Xfpc relation because of its small volume fraction in comparison with ferropericlase.
The mean interparticle spacing (\(\bar{r}=1/{\rho }^{1/2}\)) was calculated from the two-dimensional density of ferropericlase (where ρ is the number of ferropericlase particles per μm2). Note that \(\bar{r}\) becomes invalid for Xfpc = 0% and becomes inappropriate for the high-Xfpc samples (greater than about 30%) in which ferropericlase grains are significantly or completely interconnected (Extended Data Table 2).
The chemical compositions of bridgmanite after grain growth were analysed using an electron probe microanalyser (EPMA). An acceleration voltage of 15 kV and a beam current of 5 nA were used. The counting time was 20 s for each point analysis. An enstatite crystal and metallic iron were used as standards for Mg, Si and for Fe, respectively. The results of the EPMA analysis are listed in Extended Data Table 3.
Calculation of creep rates and viscosity
Flow laws of dislocation creep and diffusion creep
The diffusion-creep (\({\dot{\varepsilon }}_{{\rm{diff}}}\)) and dislocation-creep (\({\dot{\varepsilon }}_{{\rm{dis}}}\)) rates are calculated using flow laws of Coble and Nabarro–Herring diffusion creep54,55 and of pure-climb controlled dislocation creep56,57, respectively, based on the grain size of bridgmanite determined in this study and Si diffusion coefficients from previous studies58,59,60:
where A is a constant (A = 16/3); G is the shear modulus (about 210 GPa); Vm is the molar volume (25.5 cm3 mol−1); b is the Burgers vector (0.5 nm); Dlat and Dgb are the lattice and grain-boundary diffusion coefficients of the slowest species (Si), respectively; δ is the grain boundary width; σ is the stress; R is the gas constant; and T is the temperature55. The total creep rate is obtained by \({\dot{\varepsilon }}_{{\rm{total}}}={\dot{\varepsilon }}_{{\rm{diff}}}+{\dot{\varepsilon }}_{{\rm{dis}}}\), whereas η is calculated from \(\eta =\sigma /{\dot{\varepsilon }}_{{\rm{total}}}\). The temperature dependences of Dlat and δDgb in bridgmanite are taken from ref. 58 (the Dlat obtained in refs. 59,60 is essentially the same as those of ref. 58, whereas the δDgb is systematically measured as only a function of temperature in ref. 58; detailed parameters are given in Extended Data Table 4). Their pressure dependences are unknown and are therefore assumed to be the same as those of olivine (1.7 and 4.0 cm3 mol−1, respectively)61,62.
Uncertainty analysis
Equations (2) and (3) are well-established principles for diffusion creep and dislocation creep, respectively, in ceramic materials and are commonly used to simulate the creep rates in minerals, especially for bridgmanite24,56,57,59. The validity of equation (3) is demonstrated by recent deformation experiments on bridgmanite in the dislocation-creep regime—that is, the dislocation-creep rate simulated by equation (3) is within uncertainty, which is consistent with those obtained in deformation experiments24 (Extended Data Fig. 4a). Moreover, although deformation experiments on bridgmanite in the diffusion creep regime are impractical at present, the validity of equation (2) for diffusion creep is experimentally tested by other minerals such as olivine (figure 14 of ref. 63 and figure 9 of ref. 51) and pyroxene (Extended Data Fig. 4b).
Here we evaluate the uncertainty of the viscosity contrast between bridgmanite-enriched and pyrolitic rocks by the above calculations. The viscosity contrast is the ratio of creep rates between pyrolitic and bridgmanite-enriched rocks. Equations (2) and (3) suggest that the main uncertainties in the calculation come from the uncertainties of Dlat and δDgb. Because Dlat ≫ δDgb/d, in which d ≫ about 1 μm (ref. 58), both \({\dot{\varepsilon }}_{{\rm{diff}}}\) and \({\dot{\varepsilon }}_{{\rm{dis}}}\) become linearly proportional to Dlat as shown in equations (2) and (3). The deformation of pyrolitic rocks is dominated by diffusion creep, whereas that of bridgmanite-enriched rocks is dominated by either diffusion or dislocation creep (depending on Xfpc and σ) (Fig. 4b). If dislocation creep dominates in the bridgmanite-enriched rocks, the ratio of creep rates between pyrolitic and bridgmanite-enriched rocks becomes \({\left(\frac{1}{d\sigma }\right)}^{2}\frac{{\rm{\pi }}{\rm{A}}{{\rm{G}}}^{2}{\rm{ln}}\left(4{\rm{G}}/{\rm{\pi }}\sigma \right)}{{\rm{b}}}\). If diffusion creep dominates, the ratio is (1/d)2. Therefore, in both cases the ratios of creep rates are independent of Dlat and δDgb. The uncertainties of Dlat and δDgb (as well as their pressure and temperature dependences) thus affect only the absolute values of the simulated creep rate and viscosity, but do not affect the viscosity contrast between bridgmanite-enriched and pyrolitic rocks. As the uncertainties of the Burgers vector b and shear modulus G are negligible compared with the uncertainty of the viscosity contrast, the ratio of creep rates is only significantly controlled by d and σ. The σ in the general area of the mantle of Earth is small—that is, 0.1–1.0 MPa estimated from the velocities of upwelling and downwelling flows48 and 0.02–0.3 MPa based on the deformation experiments of bridgmanite24. With σ ≤ 1.0 MPa and Xfpc ≤ 5% in bridgmanite-enriched rocks, the grain-size contrast always results in a viscosity contrast by more than one order of magnitude (Fig. 4c).
The pressure dependences of Dlat and δDgb, which are unknown, may affect the variation of η with depth. Therefore, in addition to the calculations in Fig. 4e in which the activation volume for Dlat (ΔV) is assumed to be the same as that of olivine, η is also calculated by assuming different ΔV values for Dlat (ΔV for δDgb has a negligible effect because Dlat ≪ δDgb/d). As shown in Extended Data Fig. 5, ΔV affects the slope of the η–depth profile—that is, η slightly decreases with increasing depth when ΔV is 0–1 cm3 mol−1 and increases with depth when ΔV is 1–3 cm3 mol−1. However, it does not affect the viscosity jump at around 1,000-km depth, which is reasonable because in the case of either large or small ΔV, Dlat varies continuously with depth because the pressure and temperature increase continuously with depth. By contrast, ΔV > 3 cm3 mol−1 is unlikely because η would increase by more than three orders of magnitude with depth from 660 to 2,000 km, which disagrees with the mantle viscosity profile estimated from geoid observations (Extended Data Fig. 5d).
Data availability
The data of this manuscript are available at https://doi.org/10.5281/zenodo.7804779. Source data are provided with this paper.
References
Rudolph, M. L., Lekić, V. & Lithgow-Bertelloni, C. Viscosity jump in Earth’s mid-mantle. Science 350, 1349–1352 (2015).
van der Meer, D. G., van Hinsbergen, D. J. J. & Spakman, W. Atlas of the underworld: slab remnants in the mantle, their sinking history, and a new outlook on lower mantle viscosity. Tectonophysics 723, 309–448 (2018).
Fukao, Y., Obayashi, M., Nakakuki, T. & the Deep Slab Project Group Stagnant slab: a review. Annu. Rev. Earth Planet. Sci. 37, 19–46 (2009).
French, S. W. & Romanowicz, B. Broad plumes rooted at the base of the Earth’s mantle beneath major hotspots. Nature 525, 95–99 (2015).
Ballmer, M. D., Houser, C., Hernlund, J. W., Wentzcovitch, R. M. & Hirose, K. Persistence of strong silica-enriched domains in the Earth’s lower mantle. Nat. Geosci. 10, 236–241 (2017).
Gülcher, A. J. P., Gebhardt, D. J., Ballmer, M. D. & Tackley, P. J. Variable dynamic styles of primordial heterogeneity preservation in the Earth’s lower mantle. Earth Planet. Sci. Lett. 536, 116160 (2020).
Gülcher, A. J. P., Ballmer, M. D. & Tackley, P. J. Coupled dynamics and evolution of primordial and recycled heterogeneity in Earth’s lower mantle. Solid Earth 12, 2087–2107 (2021).
Allègre, C. J., Poirier, J.-P., Humler, E. & Hofmann, A. W. The chemical composition of the Earth. Earth Planet. Sci. Lett. 134, 515–526 (1995).
Peters, B. J., Carlson, R. W., Day, J. M. D. & Horan, M. F. Hadean silicate differentiation preserved by anomalous 142Nd/144Nd ratios in the Réunion hotspot source. Nature 555, 89–93 (2018).
Mundl, A. et al. Tungsten-182 heterogeneity in modern ocean island basalts. Science 356, 66–69 (2016).
Visser, K., Trampert, J., Lebedev, S. & Kennett, B. L. N. Probability of radial anisotropy in the deep mantle. Earth Planet. Sci. Lett. 270, 241–250 (2008).
Chang, S.-J., Ferreira, A. M. G., Ritsema, J., van Heijst, H. J. & Woodhouse, J. H. Joint inversion for global isotropic and radially anisotropic mantle structure including crustal thickness perturbations. J. Geophys. Res. Solid Earth 120, 4278–4300 (2015).
Fiquet, G. et al. Melting of peridotite to 140 gigapascals. Science 329, 1516–1518 (2010).
Nabiei, F. et al. Investigating magma ocean solidification on Earth through laser-heated diamond anvil cell experiments. Geophys. Res. Lett. 48, e2021GL092446 (2021).
Xie, L. et al. Formation of bridgmanite-enriched layer at the top lower-mantle during magma ocean solidification. Nat. Commun. 11, 548 (2020).
Ko, B. et al. Calcium dissolution in bridgmanite in the Earth’s deep mantle. Nature 611, 88–92 (2022).
Ballmer, M. D., Schmerr, N. C., Nakagawa, T. & Ritsema, J. Compositional mantle layering revealed by slab stagnation at ~1000-km depth. Sci. Adv. 1, e1500815 (2015).
Murakami, M., Ohishi, Y., Hirao, N. & Hirose, K. A perovskitic lower mantle inferred from high-pressure, high-temperature sound velocity data. Nature 485, 90–94 (2012).
Mashino, I., Murakami, M., Miyajima, N. & Petitgirard, S. Experimental evidence for silica-enriched Earth’s lower mantle with ferrous iron dominant bridgmanite. Proc. Natl Acad. Sci. USA 117, 27899–27905 (2020).
Ricolleau, A. et al. Density profile of pyrolite under the lower mantle conditions. Geophys. Res. Lett. 36, L06302 (2009).
Kurnosov, A., Marquardt, H., Frost, D. J., Ballaran, T. B. & Ziberna, L. Evidence for a Fe3+-rich pyrolitic lower mantle from (Al,Fe)-bearing bridgmanite elasticity data. Nature 543, 543–546 (2017).
Girard, J., Amulele, G., Farla, R., Mohiuddin, A. & Karato, S. Shear deformation of bridgmanite and magnesiowüstite aggregates at lower mantle conditions. Science 351, 144–147 (2016).
Marquardt, H. & Miyagi, L. Slab stagnation in the shallow lower mantle linked to an increase in mantle viscosity. Nat. Geosci. 8, 311–314 (2015).
Tsujino, N. et al. Viscosity of bridgmanite determined by in situ stress and strain measurements in uniaxial deformation experiments. Sci. Adv. 8, eabm1821 (2022).
Deng, J. & Lee, K. K. M. Viscosity jump in the lower mantle inferred from melting curves of ferropericlase. Nat. Commun. 8, 1997 (2017).
Shahnas, M. H., Pysklywec, R. N., Justo, J. F. & Yuen, D. A. Spin transition-induced anomalies in the lower mantle: implications for mid-mantle partial layering. Geophys. J. Int. 210, 765–773 (2017).
Yoshino, T., Yamazaki, D., Ito, E. & Katsura, T. No interconnection of ferro-periclase in post-spinel phase inferred from conductivity measurement. Geophys. Res. Lett. 35, L22303 (2008).
Civet, F., Thébault, E., Verhoeven, O., Langlais, B. & Saturnino, D. Electrical conductivity of the Earth’s mantle from the first Swarm magnetic field measurements. Geophys. Res. Lett. 42, 3338–3346 (2015).
Cordier, P. et al. Periclase deforms more slowly than bridgmanite under mantle conditions. Nature 613, 303–307 (2023).
Xu, F. et al. Deformation of post-spinel under the lower mantle conditions. J. Geophys. Res. Solid Earth 127, e2021JB023586 (2022).
Liu, Z., Ishii, T. & Katsura, T. Rapid decrease of MgAlO2.5 component in bridgmanite with pressure. Geochem. Perspect. Lett. 5, 12–18 (2017).
Brodholt, J. P. Pressure-induced changes in the compression mechanism of aluminous perovskite in the Earth’s mantle. Nature 407, 620–622 (2000).
Fei, H. et al. Pressure destabilizes oxygen vacancies in bridgmanite. J. Geophys. Res. Solid Earth 126, e2021JB022437 (2021).
Liu, Z. et al. Stability and solubility of the FeAlO3 component in bridgmanite at uppermost lower mantle conditions. J. Geophys. Res. Solid Earth 125, e2019JB018447 (2020).
Immoor, J. et al. Weak cubic CaSiO3 perovskite in the Earth’s mantle. Nature 603, 276–279 (2022).
Dannberg, J. et al. The importance of grain size to mantle dynamics and seismological observations. Geochem. Geophys. Geosyst. 18, 3034–3061 (2017).
Fei, H., Faul, U. & Katsura, T. The grain growth kinetics of bridgmanite at the topmost lower mantle. Earth Planet. Sci. Lett. 561, 116820 (2021).
Yamazaki, D., Kato, T., Ohtani, E. & Toriumi, M. Grain growth rates of MgSiO3 perovskite and periclase under lower mantle conditions. Science 274, 2052–2054 (1996).
Atkinson, H. V. Overview no. 65: theories of normal grain growth in pure single phase systems. Acta Metall. 36, 469–491 (1988).
Solomatov, V. S., El-Khozondar, R. & Tikare, V. Grain size in the lower mantle: constraints from numerical modeling of grain growth in two-phase systems. Phys. Earth Planet. Inter. 129, 265–282 (2002).
Yamazaki, D., Inoue, T., Okamoto, M. & Irifune, T. Grain growth kinetics of ringwoodite and its implication for rheology of the subducting slab. Earth Planet. Sci. Lett. 236, 871–881 (2005).
Nishihara, Y., Shinmei, T. & Karato, S. Grain-growth kinetics in wadsleyite: effects of chemical environment. Phys. Earth Planet. Inter. 154, 30–43 (2006).
Zhang, Z. & Karato, S. The effect of pressure on grain-growth kinetics in olivine aggregates with some geophysical applications. J. Geophys. Res. Solid Earth 126, e2020JB020886 (2021).
Hiraga, T., Tachibana, C., Ohashi, N. & Sano, S. Grain growth systematics for forsterite ± enstatite aggregates: effect of lithology on grain size in the upper mantle. Earth Planet. Sci. Lett. 291, 10–20 (2010).
Guignard, J., Toplis, M. J., Bystricky, M. & Monnereau, M. Temperature dependent grain growth of forsterite–nickel mixtures: implications for grain growth in two-phase systems and applications to the H-chondrite parent body. Earth Planet. Sci. Lett. 443, 20–31 (2016).
Herwegh, M., Linckens, J., Ebert, A., Berger, A. & Brodhag, S. H. The role of second phases for controlling microstructural evolution in polymineralic rocks: a review. J. Struct. Geol. 33, 1728–1750 (2011).
Katsura, T., Yoneda, A., Yamazaki, D., Yoshino, T. & Ito, E. Adiabatic temperature profile in the mantle. Phys. Earth Planet. Inter. 183, 212–218 (2010).
Karato, S.-I. Deformation of Earth Materials. An Introduction to the Rheology of Solid Earth Ch. 19, 338–362 (Cambridge Univ. Press, 2008).
Waszek, L., Schmerr, N. C. & Ballmer, M. D. Global observations of reflectors in the mid-mantle with implications for mantle structure and dynamics. Nat. Commun. 9, 385 (2018).
Fei, H. et al. A nearly water-saturated mantle transition zone inferred from mineral viscosity. Sci. Adv. 3, e1603024 (2017).
Faul, U. & Jackson, I. Diffusion creep of dry, melt-free olivine. J. Geophys. Res. Solid Earth 112, B04204 (2007).
Zandonà, A. et al. Glass-forming ability and ZrO2 saturation limits in the magnesium aluminosilicate system. Ceram. Int. 48, 8433–8439 (2021).
Rubie, D. C., Karato, S., Yan, H. & O’Neill, H. S. C. Low differential stress and controlled chemical environment in multianvil high-pressure experiments. Phys. Chem. Miner. 20, 315–322 (1993).
Nabarro, F. R. N. Steady-state diffusional creep. Philos. Mag. 16, 231–237 (1967).
Coble, R. L. A model for boundary diffusion controlled creep in polycrystalline materials. J. Appl. Phys. 34, 1679–1682 (1963).
Boioli, F. et al. Pure climb creep mechanism drives flow in Earth’s lower mantle. Sci. Adv. 3, e1601958 (2017).
Reali, R. et al. The role of diffusion-driven pure climb creep on the rheology of bridgmanite under lower mantle conditions. Sci. Rep. 9, 2053 (2019).
Yamazaki, D., Kato, T., Yurimoto, H., Ohtani, E. & Toriumi, M. Silicon self-diffusion in MgSiO3 perovskite at 25 GPa. Phys. Earth Planet. Inter. 119, 299–309 (2000).
Xu, J. et al. Silicon and magnesium diffusion in a single crystal of MgSiO3 perovskite. J. Geophys. Res. Solid Earth 116, B12205 (2011).
Dobson, D. P., Dohmen, R. & Wiedenbeck, M. Self-diffusion of oxygen and silicon in MgSiO3 perovskite. Earth Planet. Sci. Lett. 270, 125–129 (2008).
Fei, H. et al. High silicon self-diffusion coefficient in dry forsterite. Earth Planet. Sci. Lett. 345, 95–103 (2012).
Fei, H. et al. New constraints on upper mantle creep mechanism inferred from silicon grain-boundary diffusion rates. Earth Planet. Sci. Lett. 433, 350–359 (2016).
Yabe, K. & Hiraga, T. Grain-boundary diffusion creep of olivine: 1. Experiments at 1 atm. J. Geophys. Res. Solid Earth 125, e2020JB019415 (2020).
Ghosh, S., Koizumi, S. & Hiraga, T. Diffusion creep of diopside. J. Geophys. Res. Solid Earth 126, e2020JB019855 (2021).
Tasaka, M., Hiraga, T. & Zimmerman, M. E. Influence of mineral fraction on the rheological properties of forsterite + enstatite during grain-size-sensitive creep: 2. Deformation experiments. J. Geophys. Res. Solid Earth 118, 3991–4012 (2013).
Fisler, D. K., Mackwell, S. J. & Petsch, S. Grain boundary diffusion in enstatite. Phys. Chem. Miner. 24, 264–273 (1997).
Béjina, F. & Jaoul, O. Silicon self-diffusion in quartz and diopside measured by nuclear micro-analysis methods. Phys. Earth Planet. Inter. 97, 145–162 (1996).
Acknowledgements
This work is supported by the Advanced Grant of the European Research Council (ERC) under the Horizon 2020 research and innovation programme of the European Union (no. 787527) and the research grant of Deutsche Forschungsgemeinschaft (DFG) (KA3434/19-1) to T.K., the annual budget of the Bayerisches Geoinstitut and the startup funding from Zhejiang University to H.F. and the NSF grant (NSF-EAR 2125895) to U.F. We appreciate A. Zandonà (CEMHTI) for introducing the levitator facility for making silicate glasses.
Funding
Open access funding provided by Universität Bayreuth.
Author information
Authors and Affiliations
Contributions
H.F. designed the experiments, prepared the starting materials and performed high-pressure experiments, scanning electron microscope observations, EPMA analyses and data interpretation. W.C. and H.F. made the silicate glasses. H.F. initialized the geophysical implications and wrote the paper with comments from T.K., M.D.B., N.W. and U.F.; T.K. planned and organized this project; U.F. also planned the project independently and performed some preliminary experiments.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 SEM images taken from the synthesized samples.
(a) Post-spinel synthesized from olivine. The average grain size is <<0.1 μm. (b) Single phase of bridgmanite from orthopyroxene. The average grain size is 0.42 μm. (c) Bridgmanite + ferropericlase from sol-gel powder. The average grain size is approximately 0.15 μm. Insert: the whole view of this sample. The distribution of ferropericlase is inhomogeneous in the sol-gel sample. The sample consists of different domains with various Xfpc, but the Xfpc in each domain is homogenous. (d) Bridgmanite + ferropericlase synthesized from glass with grain size of about 0.2 μm. Because of bridgmanite amorphization, it is not possible to take high-magnification and high-resolution images for (a), but the grain sizes are clearly much smaller (more than three times) than those after the grain growth runs (Extended Data Table 1) and d0 is therefore negligible in Eq. (1).
Extended Data Fig. 2 The grain size of ferropericlase increases with increasing experimental duration for both low Xfpc (~ 3 – 3.5%) and relatively-high Xfpc (~18.5%) samples.
With increasing duration from 1.5 to 100 min, the grain size of ferropericlase increases by a factor of ~1.6 (from 0.38 to 0.60 μm) and 1.8 (from 0.46 to 0.85 μm), respectively, for the Xfpc = 3 – 3.5% and Xfpc = ~18.5% samples. These rates are slightly lower but within error comparable with that of bridgmanite, which increases by a factor of ~1.9 (from 1.55 to 2.98 μm and from 0.67 to 1.30 μm as given in Extended Data Table 2).
Extended Data Fig. 3 The grain size of bridgmanite (log d), interparticle spacing of ferropericlase (\(\bar{r}\)), and ferropericlase volume fraction (Xfpc).
(a) The log d increases with increasing \(\bar{r}\). (b) the \(\bar{r}\) is inversely proportional to Xfpc. The increase of \(\bar{r}\) with duration indicates the coarsening of ferropericlase, while the correlation between logd and \(\bar{r}\) indicates the simultaneous Ostwald ripening of ferropericlase and growth of bridgmanite. All the data with meaningful \(\bar{r}\) from Extended Data Table 2 are plotted.
Extended Data Fig. 4 Consistency of creep rates simulated by Eqs. (2, 3) (solid lines) and measured by deformation experiments (dash lines).
(a) Dislocation creep rate in bridgmanite from Eq. (3) and from experiments by Tsujino et al. 24 (b) Diffusion creep in pyroxene from Eq. (2) and from experiments by Ghosh et al. (diopside)64 and Tasaka et al. (enstatite)65 adjusted to a stress of 30 MPa and grain size of 1 μm (equivalent to the experimental conditions in refs. 64,65). The Si diffusion data for the calculations are from Xu et al. (DSilat in bridgmanite)59, Fisler et al. (DSigb in enstatite)66, and Bejina and Jaoul (DSilat in diopside)67. Note that Ghosh et al. 64. concluded the inconsistency of diffusion creep rates between calculations and experiments in diopside, however, they did not consider the Coble creep regime, which is not negligible in their small-grain-size samples (~1 μm). Additionally, the consistency in olivine is already demonstrated previously (Fig. 14 in ref. 63. and Fig. 9 in ref. 51).
Extended Data Fig. 5 Calculated relative viscosity as a function of depth in the lower mantle by assuming different activation volumes (ΔV = 0 – 3 cm3/mol) for DSilat.
The red and blue curves represent the viscosity from calculations and from geoid analysis1, respectively. The calculated viscosity is based on Eq. 2 and Eq. 3 with grain size variation with depth along a lower-mantle geotherm47 after 4.5 Gyr and stress condition of 1.0 MPa. Note that the viscosity profiles in the figure only represent the relative changes of viscosity with depth, but not the absolute value of viscosity in the lower mantle.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fei, H., Ballmer, M.D., Faul, U. et al. Variation in bridgmanite grain size accounts for the mid-mantle viscosity jump. Nature 620, 794–799 (2023). https://doi.org/10.1038/s41586-023-06215-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-023-06215-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.