Abstract
Tropical forests face increasing climate risk1,2, yet our ability to predict their response to climate change is limited by poor understanding of their resistance to water stress. Although xylem embolism resistance thresholds (for example, \(\varPsi \)50) and hydraulic safety margins (for example, HSM50) are important predictors of drought-induced mortality risk3,4,5, little is known about how these vary across Earth’s largest tropical forest. Here, we present a pan-Amazon, fully standardized hydraulic traits dataset and use it to assess regional variation in drought sensitivity and hydraulic trait ability to predict species distributions and long-term forest biomass accumulation. Parameters \(\varPsi \)50 and HSM50 vary markedly across the Amazon and are related to average long-term rainfall characteristics. Both \(\varPsi \)50 and HSM50 influence the biogeographical distribution of Amazon tree species. However, HSM50 was the only significant predictor of observed decadal-scale changes in forest biomass. Old-growth forests with wide HSM50 are gaining more biomass than are low HSM50 forests. We propose that this may be associated with a growth–mortality trade-off whereby trees in forests consisting of fast-growing species take greater hydraulic risks and face greater mortality risk. Moreover, in regions of more pronounced climatic change, we find evidence that forests are losing biomass, suggesting that species in these regions may be operating beyond their hydraulic limits. Continued climate change is likely to further reduce HSM50 in the Amazon6,7, with strong implications for the Amazon carbon sink.
Similar content being viewed by others
Main
Rising temperatures and drought pose a significant challenge to the functioning of Earth’s forests and may already be changing forest dynamics globally8,9. The consequences of intensifying climate stress may be particularly marked in Amazon rainforests, which house around 16,000 tree species10, store more than 100 Pg of carbon in their biomass11 and regulate climate through their substantial exchanges of carbon, water and energy with the atmosphere12. Recent recurrent drought events across the Amazon have increased tree mortality13,14 and may be partially responsible for the long-term decline of the Amazon carbon sink15,16. Water stress over Amazonian forests is likely to intensify under future climate due to increasing temperatures, altered rainfall and increased occurrence of extreme events1,2. Thus, understanding the vulnerability of these forests to drought stress is of great importance.
Substantial evidence points to hydraulic failure, defined as a disruption of whole-plant water transport capacity due to embolism of xylem vessels17, as a key mechanism underpinning drought-induced mortality3,4,18. The vulnerability of trees to hydraulic failure is closely related to their ability to resist xylem embolism and the proximity with which they operate to critical embolism thresholds, their hydraulic safety margins (HSMs)4,5. Commonly used metrics of embolism resistance include the xylem water potentials at which 50% (\(\varPsi \)50) and 88% (\(\varPsi \)88) of stem hydraulic conductance are lost, whereas HSMs integrate these embolism resistance thresholds with in situ atmospheric vapour pressure and soil water status, through several physiological and allometric traits19,20 and denote how close midday water potentials measured at the peak of the dry season (\(\varPsi \)dry) in the field approach \(\varPsi \)50 (HSM50) or \(\varPsi \)88 (HSM88)4,18,21. Thus, HSMs provide a combined measure of xylem vulnerability and exposure to water deficit. These properties have been shown to be important predictors of mortality under drought22 and are central to efforts to understand and mechanistically model climate change impacts on vegetation function8,23,24,25
Several recent studies have evaluated tree hydraulic properties within3,26,27,28,29,30,31,32,33 and between sites6,34 in the central and eastern Amazon. However, most of these sites share broadly similar climate, are located on highly weathered, infertile soils and are amongst the least dynamic Amazonian forests35,36. A basin-wide perspective of how hydraulic properties vary across Amazonian forests, which encompass a broad range of geographic/climatic conditions and species composition, is lacking at present, limiting understanding of how climate change will impact this critical ecosystem.
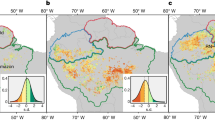
Here, we present a pan-Amazon dataset of plant hydraulic properties (\(\varPsi \)50, HSM50 and \(\varPsi \)dry), following a fully standardized methodology. Our dataset includes hydraulic traits (HTs) from 129 species across 11 forest plots in the eastern, central eastern and southern Amazon. Our sampling spans the entire Amazonian precipitation space ranging from ecotonal forests at the biome edges with long dry season length (DSL) to ever-wet aseasonal forests (Fig. 1, Extended Data Fig. 1 and Supplementary Table 1). In each site, sampling effort was concentrated on adult dominant canopy and subcanopy species (Supplementary Table 2). For each species at each site, we constructed xylem embolism vulnerability curves (describing the reduction in hydraulic conductivity with declining water potential), from which we determined \(\varPsi \)50 and \(\varPsi \)88 and also measured midday leaf water potential during the peak of the dry season (\(\varPsi \)dry; Extended Data Fig. 2) to compute hydraulic safety margins (HSM50 = \(\,\varPsi \)dry − \(\,\varPsi \)50). Collectively, the species sampled encompass a wide array of life-history strategies37 and represent about 24% of total Amazon tree biomass, excluding palms38 (Extended Data Fig. 3).
The map depicts long-term climatical water deficit (CWD) obtained from ref. 63 (2.5 arcsec resolution). Bar graphs show mean precipitation per month (1998–2016) per site. The red lines at 100 mm represent the definition of dry season, where the monthly precipitation is below 100 mm. Precipitation data were obtained from TRMM (the Tropical Rainfall Measuring Mission—TMPA/3B43 v.7) at 0.25° spatial resolution64. Aseasonal ever-wet sites (blue bars): Sucusari (SUC) and Allpahuayo (ALP-1 and ALP-2). Intermediate DSL sites (green bars): Acre (FEC), Caxiuanã (CAX), Manaus (MAN), Tambopata (TAM) and Tapajós (TAP). Ecotonal long DSL sites (brown bars): Kenia (KEN-1 and KEN-2) and Nova Xavantina (NVX).
We use this dataset to assess basin-wide biogeographic variation in embolism resistance and vulnerability to hydraulic failure. Finally, we take advantage of standardized long-term inventory plots distributed across the Amazon39, within which our sites are nested, to test whether these traits predict Amazonian species distribution and long-term aboveground biomass (AGB) accumulation (that is, the forest AGB carbon sink).
Hydraulic traits distribution
Our analyses suggest a strong overarching effect of water availability on HTs across Amazonian forests, both in terms of species level and community values. As expected, species found in ever-wet aseasonal forests (DSL of 0 months) have the least resistant xylem (least negative \(\varPsi \)50), whereas forests with intermediate DSL (2–5 months) and ecotonal long DSL forests (DSL of more than 5 months) have species with progressively more resistant (more negative \(\varPsi \)50) xylem tissue (P < 0.0001; Fig. 2 and Extended Data Fig. 4). The same pattern is observed for \(\varPsi \)dry, whereby species in long DSL forests experience more negative \(\varPsi \)dry than those in intermediate DSL or ever-wet aseasonal forests (P < 0.0001; Fig. 2 and Extended Data Fig. 4). Contrary to the convergence in HSM50 reported by previous21,40 (but not all41) studies across woody species at continental and global scales, we find that HSM50 varies significantly across Amazonian forests (P < 0.0001; Fig. 2 and Extended Data Fig. 4). Species in ever-wet aseasonal forests generally have higher HSM50 than those in intermediate DSL and long DSL forests and thus face the lowest apparent risk of hydraulic failure despite having xylem that is least resistant to embolism. This may reflect a lack of exposure to drought in ever-wet forests. Similar patterns are also observed at the community level. Across all sites, basal area weighted HT are strongly related to maximum cumulative water deficit (MCWD; Extended Data Fig. 4), which alone explains 59%, 47% and 82% of the observed variation in \(\varPsi \)50, HSM50 and \(\varPsi \)dry (linear model: P = 0.004, P = 0.01, P < 0.0001), respectively. Drier sites are generally more resistant to embolism but have lower HSM than do wetter sites, in agreement with recent global analysis41. Many species in the driest sites have negative HSM50 (Fig. 2b), suggesting that (1) they may be adapted to cope with seasonal exceedance of HSM50 and (2) mortality thresholds in these regions may be associated with higher conductance losses; for example, HSM88 as has been reported in experimental studies5,42. Although our results point to a very strong control of background climate (MCWD) in driving variation in hydraulic properties across the Amazon, we note that other factors governing water availability locally are also probably important, including topography-associated variation in water table depth28,43.
a,d, Xylem water potential at which 50% of the conductance is lost (\(\varPsi \)50). b,e, HSMs related to \(\varPsi \)50 (HSM50 = \(\varPsi \)dry − \(\varPsi \)50). c,f, In situ dry season leaf water potential (\(\varPsi \)dry). d–f, Show hydraulic trait variation within intermediate DSL forests, subsetted according to Amazon region (central eastern Amazon: TAP, CAX and MAN; western Amazon: FEC and TAM). Dashed lines denote the mean value of each trait across all tree taxa in the dataset whereas the red line indicates HSMs equal to zero. Boxplots show the 25th percentile, median and 75th percentile. The vertical bars show the interquartile range ×1.5 and datapoints beyond these bars are outliers. Sites are sorted according to increasing water availability. Red, green and blue colours represent sites from ecotonal long DSL, intermediate DSL and aseasonal ever-wet forests, respectively. Each point represents one species per site (Ntotal = 170 species). Significant differences at P < 0.05 are shown on the figure (Wilcoxon rank sum tests).
The relationship between community mean HSM50 and MCWD is unlikely to be driven by differences in leaf phenology across sites. Within our dataset, we find that deciduous species have lower HSM50 than do semideciduous and evergreen species (Extended Data Fig. 5), consistent with other findings that deciduous species have hydraulically riskier strategies44. However, the relationship between HSM50 and MCWD remains, even when deciduous and semideciduous species are excluded from the analysis (P = 0.02, R2 = 0.44; Extended Data Fig. 5). Thus, deciduousness may partially explain the low HSM50 observed in the dry fringes of the Amazon but further explanations are required. In these regions, where climate change is most accentuated, trees may now be operating at their physiological limits.
Within intermediate DSL forests, despite relatively similar MCWD and annual rainfall, species in central eastern Amazon have more resistant xylem and have wider HSM50 than their generally more dynamic western Amazon counterparts (P = 0.001; Fig. 2). Indeed, whereas resistance to embolism of intermediate DSL forests in western Amazon (mean \(\varPsi \)50 = −1.77 ± 0.13 MPa) is similar to that of aseasonal forests (mean \(\varPsi \)50 = −1.61 ± 0.1 MPa), intermediate DSL forests in central eastern Amazon (mean \(\varPsi \)50 = −2.40 ± 0.15 MPa) have embolism resistance similar to ecotonal forests in southern Amazon (mean \(\varPsi \)50 = −2.59 ± 0.18 MPa). On the other hand, \(\varPsi \)dry does not significantly differ between these forests (P = 0.5), indicating that western Amazon forest species do not compensate for their more vulnerable xylem through tighter leaf water potential regulation . Rather, western Amazon species show markedly lower HSM50 (mean HSM50 = −0.07 ± 0.14 MPa) than do central eastern species occupying a similar climatic niche (mean HSM50 = 0.58 ± 0.19 MPa, P = 0.01).
HTs explain Amazon tree biogeography
It has been shown previously that the distribution of tree species in western Amazon is strongly modulated by water availability, with some species associated with wet environments and others with dry45. We find a positive relationship between all evaluated HTs and species water deficit affiliation (WDA)45, defined as species preference for wet or dry habitat on the basis of its relative abundance across the precipitation space over which it is found (Fig. 3). Taxa with more negative WDA (dry-affiliated taxa) are widely spread in the Neotropics45. Although dry-affiliated taxa can in principle also occur in wet places, this is not true for most Amazonian species, which are highly wet-affiliated and not found in drier environments45. As expected, we find a significant positive relationship (R2 = 0.52, P < 0.0001) between \(\varPsi \)dry and WDA (Fig. 3); that is, species associated with drier bioclimates experience more negative water potentials. A significant relationship between \(\varPsi \)50 and WDA (R2 = 0.23, P < 0.0001) further reveals that the xylem of species found in drier climates is more adapted to deal with lower water potentials than that of wet-affiliated species. These findings are qualitatively consistent with a worldwide study showing that conifer species occurring in drier climates have xylem that is more resistant to embolism than those found in more mesic climates46. However, we still find a weak positive relationship between HSM50 and WDA (R2 = 0.11, P = 0.005), such that dry-affiliated species have lower HSM50 than do wet-affiliated species and thus face greater hydraulic risk (Fig. 3). Continuation of drying trends observed in the southern Amazon47 will probably further reduce \(\varPsi \)dry and HSM50 of tree species found in this region, assuming limiting acclimation in \(\varPsi \)50, as documented by other authors (for example, ref. 30).
a–c, Embolism resistance \(\varPsi \)50 (a), hydraulic safety margin HSM50 (b) and minimum leaf water potential observed in the dry season \(\varPsi \)dry (c). Individual points indicate species mean trait values (n = 87). Less negative WDA values denote wet-affiliated species and more negative WDA denote dry-affiliated species. Species-level WDA data were obtained from ref. 45. SMA regressions are shown by solid lines. The grey shaded areas represent the 95% bootstrapped confidence intervals for the slopes and intercepts. The R2 of each regression is shown on the figure. For this analysis, we subset our dataset to include only species collected in the western Amazon as done by ref. 45.
HSMs predict Amazonian carbon balance
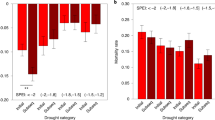
Forests across the Amazon have been gaining biomass in recent decades and this substantial carbon sink is estimated to account for 10–15% of the terrestrial land sink15,48. Forest inventory plots spread across the Amazon have revealed that Amazon forests vary widely in their biomass accumulation rates (ΔAGB, the difference between biomass gained by productivity and that lost by mortality) but the underlying mechanisms governing variation in ΔAGB across forests remain elusive15,16. We tested the predictive power of basal area weighted mean values of a range of plant traits including stem and branch wood density (WDstem and WDbranch), leaf mass per area (LMA) and HTs (\(\varPsi \)50, HSM50 and \(\varPsi \)dry), as well as climate metrics (for example, MCWD, mean annual precipitation (MAP) and mean annual temperature (MAT)) and found HSM50 to be the only significant predictor of the long-term aboveground net biomass change (ΔAGB) across forest plots (Fig. 4, Extended Data Fig. 6 and Supplementary Table 3). Although we cannot rule out the role of predictors for which we had no data (for example, root traits or pathogen status), this result highlights a key role for HSM50 in regulating forest dynamics (Extended Data Fig. 7 and Supplementary Table 4) and holds true when the analysis is repeated using dynamics data from a larger set of plots (clusters) located within the same landscape as the plots sampled directly for HTs (Extended Data Fig. 8 and Supplementary Tables 5 and 6).
a, Variance explained by individual predictors when using SMA models to predict plot-level relative ΔAGB, with ΔAGB calculated as (AGBend − AGBstart)/period of monitoring length/standing woody biomass. Climatic data (MAT, MAP and MCWD), HTs (\(\varPsi \)50, \(\varPsi \)dry and HSM50, defined as the difference between \(\varPsi \)dry and \(\varPsi \)50) and other plant traits (stem and branch wood density and LMA) are indicated as red, blue, brown and green bars, respectively. Asterisk denotes statistically significant bivariate relationships after correcting for multiple hypothesis testing, using Bonferroni-corrected P < 0.05. Stem wood density values were extracted from the Global Wood Density database65,66. Bivariate plots and statistics for all predictor variables considered are shown in Extended Data Fig. 6 and Supplementary Table 3. b, Relationship between basal area weighted mean HSM50 and plot-level relative ΔAGB. We computed relative ΔAGB due to high standing AGB variance across plots. However, we also repeated B regression by considering absolute ΔAGB and this result was independent of whether absolute or relative ΔAGB were used in the bivariate regressions (Extended Data Fig. 7d). c, Relationship between basal area weighted mean HSM88 and annual instantaneous stem mortality rate (equation (4); ref. 67) across forest plots. The solid line is the best fit line of the SMA model and the shaded area represents the 95% bootstrapped confidence interval. KEN plots were excluded from all forest dynamics analyses because of a fire event that occurred in the region in 200468 and may still be affecting biomass accrual.
HSM50 explained 70% of the variance in relative ΔAGB across Amazon forest plots and 67% of the absolute ΔAGB (P < 0.01 and P < 0.01, respectively, Extended Data Fig. 7 and Supplementary Table 4). Tree communities characterized by narrow HSM50 are gaining less biomass than those with high HSM50. Unravelling the physiological mechanisms underpinning the relationship between HSM50 and ΔAGB is challenging. The ΔAGB depends on the balance of productivity and mortality and HSM50 might be expected to affect both of these pathways. Uptake of CO2 for photosynthetic assimilation and transpirational water loss from leaves are directly coupled through stomata. The economic challenge of guaranteeing carbon gain although minimizing water loss gives rise to a range of plant strategies depending on resource availability49, with plants with acquisitive characteristics at one end of the spectrum to those with conservative characteristics at the other. Previous studies have shown that species with higher growth rates50 or with acquisitive trait attributes51 have lower HSMs. Using species-level diameter growth data from across the Amazon37, we also find a negative relationship with HSM50 (Extended Data Fig. 9). At the community scale, we generally find a stronger association of HSMs with mortality processes than with productivity, suggesting that HSM controls on mortality may be particularly important in regulating stand-level carbon balance. For example, both plot-level and cluster-level analyses show tighter relationships between HSM50 and relative AGB mortality (R2 of 0.26 and 0.27) than with relative AGB productivity (R2 of 0.00 and 0.02) (Extended Data Figs. 7 and 8), with the same patterns observed when HSM88 is considered instead of HSM50 (Extended Data Fig. 10 and Supplementary Table 4). We also find strong relationships between HSMs (HSM88 in particular) and woody biomass residence time (Extended Data Fig. 10). Relationships between HSM50 and stand-level stem mortality rates are invariably stronger than with biomass mortality metrics (plot level R2 = 0.47, P = 0.04; cluster level R2 = 0.47, P = 0.06) and are even stronger for HSM88, which was found to explain 68% of the variation in mortality rates at plot level (Fig. 4c;R2 = 0.68, P < 0.01), with similar patterns observed in the cluster-level analysis. These results indicate that exceedance of HSM88 greatly increases mortality risk and is consistent with experimental findings on saplings42.
We propose that the relationship between HSM and ΔAGB (Extended Data Fig. 7a,d) may be mediated mainly through HSM controls on woody biomass residence time (τw), which in turn modulates forest response to a CO2 stimulus. Forests with high τw are expected to sustain CO2-induced net carbon gains for a longer period of time than forests with shorter τw as the lag times between productivity increases and knock-on increases in mortality are longer in high τw forests52,53. We find that forests with low HSM50/HSM88 tend to be associated with higher woody biomass turnover rates/lower woody biomass residence times (τw; Extended Data Figs. 7h, 8h and 10h) but are often more productive than high HSM forests. In line with theoretical expectations, high τw forests have been found to be losing less biomass in the Amazon than those with low τw (ref. 16). High HSM50 may promote higher τw by reducing the risk of exceeding critical embolism resistance thresholds associated with tree mortality.
It has recently been proposed that HSM may also help to explain the growth–survivorship trade-off which is manifested at plot and at species level across the Amazon, whereby forests characterized by species with acquisitive traits that prioritize growth take greater hydraulic risks (that is, operate at lower HSM) and are more prone to mortality during periods of moderate water stress54. Our results support this as we find that species with high growth rates have low HSM50 (Extended Data Fig. 9), providing a potential mechanistic explanation for recent findings that high species-level growth rates are the principal mortality predictor for trees across the Amazon55. This HSM-mediated growth–survivorship trade-off also provides an explanation for why forests on more fertile, western Amazon forests have higher mortality rates than those in slower, less fertile central eastern Amazon forests36,55 as we find lower HSM in western Amazon forests occurring in a similar rainfall space to those in central eastern Amazon.
HSM50 reflects exposure to drought stress as well as plant water use strategies. Intensifying climate stress may help to explain why plots with the most negative HSM are losing rather than gaining biomass. The most vulnerable site (lowest HSM) in our study is in the southern fringe of the Amazon, the driest region of the Amazon and also the one that has also faced the greatest recent climatic changes2,12. The very low HSM50 observed there points to substantial hydraulic stress and may indicate that this region of the Amazon faces the most imminent climate risk. Our finding that forests in this region are losing biomass (Fig. 4b), is consistent with recent results based on analysis of atmospheric CO2 profiles that suggest remaining forests in the south eastern Amazon no longer act as a large-scale carbon sink56.
Implications and conclusions
Our study evaluates large-scale variation in plant hydraulic properties across the Amazon. Our results provide compelling evidence for the importance of these properties in influencing basin-scale forest composition and function and offer important new insights into which Amazonian forests face greatest risk of drought-induced mortality. Although more resistant xylem (more negative \(\varPsi \)50) may provide Amazon species with an evolutionary adaptation to persist in water-limited environments, our results indicate that HSM50 is a powerful integrative trait that is strongly related to long-term ecosystem-scale biomass trajectories. We find that climatic factors alone or other plant traits do not have this explanatory power, in line with previous work suggesting that community-level variability in HSM50 exerts a strong control on ecosystem resilience to drought57. Although there are inevitable uncertainties (for example, precise determination of minimum water potential requires continuous measurements58 and other portions of the tree hydraulic pathway may show different sensitivities to water stress59,60), the fully standardized dataset allows direct comparison of the drought vulnerability of forests across the Amazon. We find that central eastern forests that have informed most of our current understanding of Amazon drought impacts are the least vulnerable to drought, possibly due to the periodic occurrences of El Niño/Southern Oscillation events and high climate variability creating a selection pressure for more drought-adapted taxa61,62. Of all sites considered in this study, the Tapajós site located close to one of the Amazon ecosystem-scale drought experiments has the most resistant \(\varPsi \)50 and the most positive HSM50, suggesting that upscaling of drought sensitivity inferred from these forests to the whole biome may underestimate Amazonian sensitivity to climate change. Continued increases in temperature and vapour pressure deficit, as predicted by all climate models, will probably reduce safety margins across Amazonian forests6,31 and further threaten the already declining Amazon carbon sink15,56. Our results indicate that these effects will be most marked in fast-turnover forests in western Amazon and increasingly stressed forests in the southern Amazon, which may already be at their physiological limit.
Methods
Site description
We assemble a pan-Amazon dataset of key HTs (\(\varPsi \)50, HSM50 and \(\varPsi \)dry), including 129 species distributed across 11 forest sites (Fig. 1 and Extended Data Fig. 1). The sites are old-growth lowland forests (less than 400 m of elevation), with no evidence of significant human disturbance, located in western, central eastern and southern Amazon. They were specifically chosen to span the full Amazonian precipitation gradient and to encompass the principal axes of species composition in the Amazon. The MAP varied from around 1,390 to around 3,170 mm yr−1 and mean MCWD varied from −640 to −15 mm across sites. Summary information for all sites can be found in Supplementary Tables 1 and 2.
Species selection
To characterize drought sensitivity across a wide set of species and strategies, we sampled the most dominant adult canopy and subcanopy tree species at each site. For TAP, MAN and CAX, we used published data from refs. 6,27,30 which follow the same methodology as this study. The sampling effort at each site varied from 7 to 26 species which represented between 14% and 70% of the total basal area (Supplementary Table 2). Sites for which less than 30% of the total basal area was sampled (ALP-1, ALP-2, SUC, CAX and MAN) are hyperdiverse forests and lack the clear dominance structure by a few species observed in less diverse plots (for example, in the southern Amazon NVX site, the seven species sampled account for more than 50% of the basal area). Previous work by ref. 6, show that the MAN site, despite having the lowest sampled basal area of all sites presented in this study (about 14%) is representative of the broader floristic community, as adding a broader array of species-level hydraulic trait data did not significantly change basal area weighted mean (CWM) values. The same study found that mean species values are not likely to differ from community mean values if (1) species dominance is not driven by a few species, (2) traits have low dispersion around the mean (low standard deviation compared to the mean) and (3) traits are randomly distributed across species dominance distributions. For the other four sites for which sampled coverage was less than 30%, these criteria are generally satisfied (for example, cumulative dominance of the five most dominant species at ALP-1 is 27.9%, ALP-1 26.2%, SUC 15.0% and CAX 10.7%, standard deviation of \(\varPsi \)50 is between 32% and 49% of the mean value at each site and there is no relationship between species dominance and HT. Thus, basal area weighted mean trait values for the 11 sites probably well represent the broader unsampled community of trees.
Abiotic data
To characterize climatological water deficit at each site, we calculated the MCWD69, which is a widely used measure of dry season intensity for Amazon forests13,16,70 that expresses the cumulative water stress experienced within an average year69. The MCWD metric assumes that a forest experiences water deficit if monthly precipitation does not meet evapotranspirational requirements and accumulates that deficit over all successive months with rainfall lower than evapotranspiration (E) values69. Monthly water deficit (WDn) was then calculated as the difference between precipitation (P) and evapotranspiration demand in each month n. MCWD was computed as the maximum monthly cumulative water deficit (CWD) experienced over an average year, for which the change in water deficit in any given month n is calculated as the difference between precipitation falling that month (Pn) and an assumed evapotranspiration demand (En, mm month−1). For any given month n,
As all of our plots are in the southern hemisphere, their hydrological year coincides with the calendar year, allowing us to start our MCWD calculations at the beginning of each calendar year. For statistical analyses, we use the long-term mean MCWD for each location. Monthly precipitation data were obtained from the tropical rainfall measuring mission (TRMM TMPA/3B43 v.7)64 at 0.25° spatial resolution from 1998 to 2016. To estimate evapotranspiration, we used monthly ERA-5-Land Reanalysis E data at 0.1° spatial resolution from 1998 to 201671, as this product has been suggested to well represent evapotranspiration estimates in the Amazon72. To have one value of evapotranspiration demand per site (En in equation (1)), we used the mean E value for the 3 months with highest E across years. Mean annual temperature data at 1 km spatial resolution were obtained from Worldclim2 (ref. 73).
We performed an alternative assessment computing MCWD on the basis of MOD16 (ref. 74) evapotranspiration product and on E estimation of 100 mm per month69 and we also computed MAP on the basis of TRMM64 and CRU75 data. The main results remained similar, independent of the climate product used (Supplementary Table 7).
Collection of plant material
One fully sun-exposed top-canopy branch (or branch at the maximum height reachable by climbers) was collected from, on average, three individuals of each species at each site for subsequent construction of xylem vulnerability curves. The same or a second set of branches, in the same canopy position, was used to extract samples of wood density and LMA. For embolism resistance determination, data collection was undertaken during the wet season, when forests were maximally hydrated. Branches (more than 1 m long) were harvested during predawn or very early in the morning, to capture a fully hydrated starting point. Immediately after collection, basal portions of branches were wrapped with a wet cloth and branches were placed in a humidified opaque plastic bag to avoid desiccation during transport. Bags were sealed and carried to the field station for determination of xylem vulnerability curves. For samples not collected during predawn, branches were placed in a bucket, recut under water, covered with an opaque plastic bag and left to rehydrate for at least 5 h.
Xylem embolism resistance (\(\varPsi \) 50 and \(\varPsi \) 88)
To quantify xylem resistance to embolism of Amazonian trees species, we focused on the water potentials associated with \(\varPsi \)50, given its wide use as a critical embolism resistance threshold4,5. To derive this parameter, we constructed xylem vulnerability curves by simultaneously measuring percentage of embolism formation and xylem water potential under progressive desiccation76. We estimated embolism using the pneumatic method of ref. 77, which quantifies the air extracted from within branches at each stage of dehydration and expresses this as a percentage of air discharge (PAD), defined as the percentage difference between the maximum amount of air removed under extreme dehydration (100% PAD) and the minimum amount removed under maximum hydration (0% PAD)78. For our measurements we used manual, self-constructed pneumatic devices, following ref. 78. Although automated devices for measuring air discharge are now available, these were not available at the time of our data collection. For all air discharge determinations, we applied the protocol of ref. 77 whereby measurements of air discharge were made over a 2.5 min interval. We note that the absolute volumes of air discharged are sensitive to the time interval of the discharge measurements, as shown by ref. 79,who report a difference of about 10% on the absolute air discharge measured for 15 s versus 115 s. There are still methodological uncertainties that require further investigation, including how the contribution of extraxylary discharge varies across different Amazonian species. Recent work using a pipe pneumatic model to simulate gas diffusion from intact conduits suggests that the overriding source of discharged air is from embolized xylem vessels although there is a small contribution (estimated to be about 9% over 15 s of discharge) from extraxylary pathways80. It is also important to note that the method measures embolism from vessels connected to the cut end of the branch from which gas is sampled and that there may be more embolism from vessels that are not directly connected to the cut end80. However, embolism spread during the branch dehydration method for embolism induction used in this study is expected to be predominantly from the cut branches76 and is corroborated by the strong agreement between petiole embolism status using the pneumatic method and leaf vein embolism assessed using optical approaches81.
The portability, ease of use and low cost of the pneumatic method make it ideally suited for use in remote tropical environments in which laboratory infrastructure is often minimal. Several studies have shown that \(\varPsi \)50 values derived from the pneumatic approach agree closely with those derived using more laborious methods77,79,81,82,83,84. For the TAP site in this study, \(\varPsi \)50 determinations based on the pneumatic method were compared with values derived from xylem vulnerability curves of percentage loss of conductance (PLC) constructed using a hydraulic ultralow flow meter85 and found a strong agreement (R2 = 0.83) between both methods84, further corroborating findings from previous studies (refs. 27,84 provide detailed description of the hydraulic method used). Although one study86 (but see refs. 84,87) proposed that the method may be unsuitable for long-vesseled species, we find no evidence of any vessel length bias in our \(\varPsi \)50 estimates derived from the pneumatic method (standard major axis (SMA) regression \(\varPsi \)50 versus maximum vessel length: P = 0.15, R2 = 0.02).
The initial PAD measurement for each branch was made immediately after removing the branch from a sealed opaque plastic bag to ensure that vulnerability curves started from a maximally hydrated state. Subsequent measurements were then conducted successively throughout the dehydration process, with approximately eight to ten measurements per individual used to construct each curve. Branches were progressively dried through the bench dehydration technique76. Between each dehydration state, branches were bagged for a minimum of 1 h to equilibrate leaf and xylem water potentials. Leaf water potential (used as a proxy for xylem water potential following equilibration) was measured with a pressure chamber (PMS 1505D and PMS 1000, PMS instruments).
We used the exponential sigmoidal function of ref. 88 to calculate \(\varPsi \)50 for each species at each site:
where S is the slope of the curve, Ψx is xylem water potential (MPa) and Ψ50 is Ψx corresponding to a PAD of 50%.
Following ref. 89, we computed Ψ88 as:
\({\boldsymbol{\Psi }}\) dry and HSMs
To calculate how close Amazonian trees operate to critical embolism thresholds in nature, we measured in situ midday leaf water potentials during the peak of the dry season (\(\varPsi \)dry). Sampling campaigns closely corresponded with the time of most intense water deficit (Extended Data Fig. 2) and the year of sampling was not climatologically anomalous. We sampled three to six top-canopy fully expanded and sun-exposed leaves per individual (three individuals per species for 129 species in total across 11 sites) from 11:00 to 14:30. Parameter \(\varPsi \)dry was measured with a pressure chamber (PMS 1505D and PMS 1000, PMS instruments) in situ immediately postsampling and the values of different leaves averaged per individual. In our protocol we tried to minimize the time spent between branch cutting and the leaf water potential measurement with the pressure chamber (around 3–5 min). We collected branches (40–60 cm in length, depending on the species and leaf size) that were fully exposed to light from the top part of the canopy (highest part that the climbers could reach), from apparently healthy and undamaged individuals. Telescopic shears (normally four to six poles, with total length of 5–7 m) were used to access and cut the branches. As soon as the branches hit the ground, the branches were bagged in a black and opaque plastic bag and transported to the pressure chamber, which was located inside the plot. We then collected three to six healthy and fully expanded leaves for each individual and immediately (after the cut) placed them into the pressure chamber. All of the processes were made as quickly as possible to avoid dehydration.
Because of pressure drops in transpiring leaves, we note that the water potentials measured are probably lower than the branch water potential values at the time of measurement. Apart from aseasonal ever-wet forests, which have no climatological dry season (monthlyprecip < 100 mm), data collection took place in the peak of dry season (Extended Data Fig. 2) during what were climatically normal years. For each species at each site we calculated the HSM with respect to \({\varPsi }_{50}\) (HSM50), as the difference between species-level \(\varPsi \)dry, taken as the minimum \(\varPsi \)dry value of all individuals for that species and \(\varPsi \)50. All \(\varPsi \)dry measurements were made in climatologically normal years. (See Supplementary Table 8 for further information of sampling dates for each site). We also calculated the HSM with respect to \({\varPsi }_{88}\) (HSM88) for all sampled species.
Wood density and leaf mass per area
We combined published and new field measurements of LMA and wood density to understand the power of these traits relative to HTs in predicting forest carbon balance. Stem wood density data (WDstem) were obtained from the Global Wood Density database65,66 and calculated as species mean values. We measured wood density at branch level (WDbranch) using a water displacement method90. In this method, branch segments of about 25 mm length and 12 mm diameter were first cut and debarked. Samples were then placed in a recipient with filtered water to rehydrate for 24 h and subsequently weighed with a three-decimal scale. After this, the sample was oven-dried for 48–72 h at 70 °C and the dry weight measured with a balance. Wood density was then expressed as the ratio of wood dry mass and wood fresh volume (g cm−3). Branch wood density measurements were made in all sites except NVX. For this site, we used stem wood density values65,66 for each of our target species.
We measured LMA for all sampled species in each of the 11 sites. For this, all leaves were detached from a selected branch and a subsample of 10–20 leaves per branch were taken, numbered and scanned. All the other leaves were kept separate to be oven-dried. This was usually done as soon as possible after returning to the field station. When it was not possible to scan the leaves straight away, we placed all the detached leaves into a sealed plastic bag in the dark and stored them for no more than 24 h. After scanning, all leaves were oven-dried for 48–72 h at around 70 °C. Once dry, the subsampled numbered leaves were individually weighed and the non-numbered leaves were weighed together with a precision scale (three decimals). On the basis of the relationship between the fresh area and dry weight of individual leaves (from the subsampled 10–20 leaves) and having the dry weight of all the leaves of the branch, we estimated the fresh leaf area corresponding to the entire branch. The LMA was then calculated as the ratio of leaf dry mass to fresh area, expressed in g m−2. We then calculated basal area weighted mean values for all these traits for each site (Supplementary Table 2). The number of species sampled for each trait is shown in the Supplementary Table 9. Further leaf habit information of sampled species is provided in Supplementary Table 10.
Water deficit affiliation
To describe Amazonian species-level biogeographical distributions, we used published WDA data45, which describes the spatial association of Amazonian tree species with climatological water availability. WDA was calculated as the mean climatological water deficit across inventory plots in which a species occurs weighted by its relative abundance in each of 513 forest plots broadly distributed in the western Neotropics45. More negative WDA values represent dry-affiliated species, whereas wet-affiliated species are represented by less negative WDA values.
Forest dynamics data
We used long-term forest plots from the RAINFOR network39 to help understand the relationship between hydraulic attributes and stand-scale carbon dynamics. Thus, we computed AGB net change (ΔAGB, Mg ha−1 yr−1), annual aboveground wood production (AGWP, Mg ha−1 yr−1), annual AGB mortality (AGBMORT, Mg ha−1 yr−1), annual instantaneous stem mortality rate (% y−1) and woody biomass residence time (τw) for the same forest plots sampled directly for HTs. For the two plots (MAN and TAP), for which we did not have access to forest dynamics data, we used information from a permanent RAINFOR network forest plot in the same landscape, with the most similar structure and species composition (BNT-01 and TAP-02, respectively; Supplementary Table 6) to our sampling plots. For CAX, we used published data by ref. 91 for the control plot. The other six plots are part of the RAINFOR network39, having been established by and/or monitored by RAINFOR partners (Supplementary Table 5). Plot data for these analyses were curated and obtained via the ForestPlots.net database92,93, for which standard quality control procedures are applied. We only included plots in the analysis that lacked a history of recent anthropogenic disturbance. For all forest dynamics analyses we excluded KEN plots because of a fire event that occurred in the region in 200468 and may still be affecting biomass stocks and dynamics. Following previous studies15,94, plots smaller than 0.5 ha that were up to 1 km apart from each other were combined and treated as a single plot (for example, TAP-54, TAP-55, TAP-56 and TAP-57 treated as TAP-02, the plot we used to represent TAP). For each plot, we only included pre-2015 El Nino censuses and selected the census start date to be as consistent as possible across plots. For this we excluded pre-2000 measurements, apart from TAP plot for which censuses were available only from 1983 to 1995. For other plots, we used the earliest census available for this plot if data collection started after 2000 (VCR-02 plot, for example, which starts in 2003). We tried to ensure that biomass dynamics metrics used in the analyses represented at least 10 yr of total monitoring time per plot. If application of the 2000 start date for a given plot resulted in fewer than 10 yr of monitoring, we also included the census date immediately before 2000 (99 for BNT-02 plot, which we used to represent MAN) to ensure at least 10 yr of monitoring (Supplementary Table 5). The monitoring time used for the plots included in the analysis was on average 12.3 (s.d. = 2.5) yr. In RAINFOR plots, all live individuals of more than 10 cm in diameter at breast height (DBH) are repeatedly measured over time, using standardized protocols, with species identified and careful records kept of trees that die or recruit from one census to the next. AGB for each census per plot was computed using the ref. 63 equation for moist forests on the basis of tree diameter, wood density and height. As local height data were often unavailable, a Weibull equation with regionally varying coefficients was used to estimate height following ref. 11. Species-level wood density values from the Global Wood Density database65,66 were used to compute AGB, AGWP and AGBMORT. For each census, biomass values were calculated for all dicotyledonous trees in the plots above the 10 cm DBH cut-off and summed to give total stand-level biomass stocks.
We estimated annual ΔAGB (Mg ha−1 yr−1) for a given plot as the difference in AGB between the final and initial census used (AGBfinal census − AGBinitial census) divided by the monitoring length (Datefinal census − Dateinitial census) in years. For each census interval per plot, we also computed annual AGWP (Mg ha−1 yr−1), following ref. 95, which encompasses (1) the sum of the growth of surviving trees, (2) the sum of AGB of new recruits, (3) the estimated sum of growth of unobserved recruits that dies and (4) the estimated sum of unobserved growth of initial trees that died, within a plot in a given census interval, divided by the census interval length (yr) (see also ref. 94). For each plot, we computed annual AGBMORT, including unobserved components, which is defined as the sum of the AGB of all dead trees, plus the estimated growth of recruits that died before they could be recorded in the second census and the sum of estimated unobserved growth of trees that died within an interval, divided by the census interval length94.
As AGB varies across sites it is useful to account for this when comparing sites. We therefore also computed relative ΔAGB (ΔAGB/AGB), relative AGWP and relative AGBMORT by dividing absolute values by the time-weighted mean standing woody biomass across censuses per plot. Both absolute and relative values are presented in the Extended Data Figs. 7, 8 and 10 and Supplementary Table 4). We computed the annual instantaneous stem mortality rate (% y−1) following ref. 67:
in which A is the number of stems per ha in the beginning of the census interval and B is the number of stems per ha that survived throughout the census interval. Owing to the sensitivity of these rates to census interval effects, we standardized them to a common census interval, following ref. 96. For all calculations above (AGB, AGWP, AGBMORT and stem mortality) we used the BiomasaFP R package97. We calculated the time-weighted mean values of all these absolute and relative parameters (AGB, AGWP, AGBMORT and stem mortality) to have one value per plot. We then calculated woody biomass residence time (τw) as the ratio of the time-weighted mean standing woody biomass and the time-weighted mean annual biomass mortality52.
To test whether relationships between HSM50 and forest dynamics at plot level apply over landscape scales and to account for the influence of within- and among-plot stochasticity in dynamics, we also we used mean forest values of forest dynamics metrics across groups of plots (clusters) in the same landscape with similar structure and composition to plots sampled for hydraulic measurements (Supplementary Tables 5 and 6). For this cluster-level analysis, we excluded white-sand forests and permanently water-logged swamp forests because they are extreme edaphic habitats, known to have a more limited and edaphically specialized tree flora98. We also excluded forests lying within active floodplains of rivers because their flora is also distinctive and, like swamp forests, they have access to more water beyond that which is climatically determined. In total, we used data from 34 long-term monitoring plots (31.37 ha of forest). For this analysis, we used cluster mean forest dynamic values (instead of plot cluster weighted mean, for example) because plot area and monitoring length did not vary considerably within clusters (Supplementary Table 5). To account for sampling effort variation across cluster of forest plot, we tested if the residuals of the relationship between relative ΔAGB and HSM50 were related to cluster mean monitoring time (mean ± s.d. was 12.1 ± 1.8 yr) and cluster total area (3.9 ± 3.0 ha). No weights were assigned to each data point in the regression because we found no evidence of relationships between the residuals and sampling effort across clusters.
Statistical analysis
To examine the distribution of HTs (\(\varPsi \)50, \(\varPsi \)dry and HSM50) across Amazonian tree taxa (N = 129 species), trait values were averaged for species occurring at several sites. We conducted statistical analyses to investigate differences in species-level hydraulic trait values among different forest types and geographical regions and also to evaluate controls of water availability on basal area weighted mean HT across the study sites. To examine differences in HTs among forest types, we first grouped our 11 forest sites into three forest types, based on DSL: (1) ecotonal long DSL forests—DSL equal to 6 months, MAP and MCWD less than 1,600 and −470 mm, respectively; (2) intermediate DSL forests—DSL ranging from 5 to 2 months, MAP between 1,990 and 2,650 mm and MCWD varying from −288 to −184 mm; and (3) ever-wet aseasonal forests—DSL about 0 months, MAP and MCWD greater than 2,950 and −15 mm, respectively (Extended Data Fig. 1 and Supplementary Table 1). To test for statistical differences in HTs across forest types, we performed a one-way Kruskal–Wallis followed by a post hoc Mann–Whitney–Wilcoxon rank sum test. Western and central eastern Amazon forests have fundamentally different dynamics in that western Amazon forests are characterized by high growth and turnover whereas central eastern forests are associated with slow growth and turnover35,36. To test for differences between species in intermediate DSL sites in western Amazon (FEC and TAM) and central eastern Amazon (CAX, MAN and TAP), we performed Wilcoxon rank sum tests. Linear models were constructed to evaluate relationships between basal area weighted mean HT and MCWD (Supplementary Table 7). For all analyses, we use a significance level of 0.05.
To investigate if species biogeographical distributions are related to mean HT, we used SMA regressions with WDA as the response variable. Following Esquivel-Muelbert et al.45, we restricted our analysis to the western Amazon as these published WDA data are based entirely on species distributions within western Amazon, helping to control for the potentially confounding effects of differences in soil and forest dynamics across Amazonian regions. Our subsample for this analysis encompassed a total of 87 species distributed across aseasonal, intermediate DSL and ecotonal long DSL forests, with MAP across plots ranging from 1,390 to 3,170 mm. SMA regressions were performed using the smatr package99 in R.
Using our entire dataset across the Amazon, we evaluated whether HTs were better predictors of Amazon forest carbon balance than climatic factors or other leaf and wood traits. More specifically, we performed bivariate SMA models to investigate relationships between HTs (\(\varPsi \)50, \(\varPsi \)dry and HSM50), climatic data (MCWD, MAP, DSL and MAT) and other functional traits (LMA, WDstem and WDbranch) versus long-term ΔAGB at plot level. We computed basal area weighted mean LMA, WDbranch and WDstem data65,66. To account for the influence of multiple testing, we applied a Bonferroni correction to P values for bivariate regressions. SMA models were further conducted to examine the relationship between HSM50 versus absolute and relative values of AGB annual woody production, AGB annual mortality, stem mortality and residence time of woody biomass. Supplementary Table 5 presents summary information per plot and clusters. All presented analyses were performed in RStudio v.1.1.423 (ref. 100).
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The pan-Amazonian HT dataset (\(\varPsi \)50, \(\varPsi \)dry and HSM50) and branch wood density per species per site, as well as forest dynamic and climate data per plot presented in this study are available as a ForestPlots.net data package at https://forestplots.net/data-packages/Tavares-et-al-2023. Basal area weighted mean LMA is shown in Supplementary Table 2. Species stem wood density data were obtained from Global Wood Density database65,66. Species WDA data were extracted from ref. 45.
Code availability
The codes to recreate the main analyses and the main figures presented in this study are available as a ForestPlots.net data package at https://forestplots.net/data-packages/Tavares-et-al-2023.
References
Duffy, P. B., Brando, P., Asner, G. P. & Field, C. B. Projections of future meteorological drought and wet periods in the Amazon. Proc. Natl Acad. Sci. USA https://doi.org/10.1073/pnas.1421010112 (2015).
Marengo, J. A. et al. Changes in climate and land use over the Amazon region: current and future variability and trends. Front. Earth Sci. 6, 228 (2018).
Rowland, L. et al. Death from drought in tropical forests is triggered by hydraulics not carbon starvation. Nature 528, 119–122 (2015).
Choat, B. et al. Triggers of tree mortality under drought. Nature 558, 531–539 (2018).
Adams, H. D. et al. A multi-species synthesis of physiological mechanisms in drought-induced tree mortality. Nat. Ecol. Evol. 1, 1285–1291 (2017).
Barros, F. V. et al. Hydraulic traits explain differential responses of Amazonian forests to the 2015 El Nino-induced drought. New Phytol. 223, 1253–1266 (2019).
Fontes, C. G. et al. Dry and hot: the hydraulic consequences of a climate change-type drought for Amazonian trees. Philos. Trans. R Soc. Lond. B 373, 20180209 (2018).
Brodribb, T. J., Powers, J., Cochard, H. & Choat, B. Hanging by a thread? Forests and drought. Science 368, 261–266 (2020).
McDowell, N. G. et al. Pervasive shifts in forest dynamics in a changing world. Science 368, eaaz9463 (2020).
Ter Steege, H. et al. Hyperdominance in the Amazonian tree flora. Science 342, 1243092 (2013).
Feldpausch, T. R. et al. Tree height integrated into pantropical forest biomass estimates. Biogeosciences 9, 3381–3403 (2012).
Nobre, C. A. et al. Land-use and climate change risks in the Amazon and the need of a novel sustainable development paradigm. Proc. Natl Acad. Sci. USA https://doi.org/10.1073/pnas.1605516113 (2016).
Phillips, O. L. et al. Drought sensitivity of the amazon rainforest. Science 323, 1344–1347 (2009).
Berenguer, E. et al. Tracking the impacts of El Niño drought and fire in human-modified Amazonian forests. Proc. Natl Acad Sci USA 118, e2019377118 (2021).
Brienen, R. J. W. et al. Long-term decline of the Amazon carbon sink. Nature 519, 344–348 (2015).
Hubau, W., Lewis, S. L., Phillips, O. L. & Zemagho, L. Asynchronous carbon sink saturation in African and Amazonian tropical forests. Nature 579, 80–87 (2020).
Tyree, M. T. & Zimmermann, M. H. Xylem Structure and the Ascent of Sap (Heidelberg, 2002).
Anderegg, W. R. L. et al. Meta-analysis reveals that hydraulic traits explain cross-species patterns of drought-induced tree mortality across the globe. Proc. Natl Acad. Sci. USA 113, 5024–5029 (2016).
Delzon, S. & Cochard, H. Recent advances in tree hydraulics highlight the ecological significance of the hydraulic safety margin. New Phytol. 203, 355–358 (2014).
Bhaskar, R. & Ackerly, D. D. Ecological relevance of minimum seasonal water potentials. Physiol. Plant. 127, 353–359 (2006).
Choat, B. et al. Global convergence in the vulnerability of forests to drought. Nature 491, 752–755 (2012).
Powers, J. S. et al. A catastrophic tropical drought kills hydraulically vulnerable tree species. Glob. Change Biol. 26, 3122–3133 (2020).
McDowell, N. G. & Allen, C. D. Darcy’s law predicts widespread forest mortality under climate warming. Nat. Clim. Change 5, 669–672 (2015).
Christoffersen, B. O. et al. Linking hydraulic traits to tropical forest function in a size-structured and trait-driven model (TFS v.1-Hydro). Geosci. Model Dev. 9, 4227–4255 (2016).
McDowell, N. G. Deriving pattern from complexity in the processes underlying tropical forest drought impacts. New Phytol. 219, 841–844 (2018).
Powell, T. L. et al. Differences in xylem and leaf hydraulic traits explain differences in drought tolerance among mature Amazon rainforest trees. Glob. Change Biol. 23, 4280–4293 (2017).
Brum, M. et al. Hydrological niche segregation defines forest structure and drought tolerance strategies in a seasonal Amazon forest. J. Ecol. https://doi.org/10.1111/1365-2745.13022 (2018).
Oliveira, R. S. et al. Embolism resistance drives the distribution of Amazonian rainforest tree species along hydro-topographic gradients. New Phytol. https://doi.org/10.1111/nph.15463 (2018).
Santiago, L. S. et al. Coordination and trade-offs among hydraulic safety, efficiency and drought avoidance traits in Amazonian rainforest canopy tree species. New Phytol. 218, 1015–1024 (2018).
Bittencourt, P. R. L. et al. Amazonia trees have limited capacity to acclimate plant hydraulic properties in response to long-term drought. Glob. Change Biol. 26, 3569–3584 (2020).
Fontes, C. G. et al. Dry and hot: the hydraulic consequences of a climate change-type drought for Amazonian trees. Philos. Trans. R. Soc. Lond. B https://doi.org/10.1098/rstb.2018.0209 (2018).
Garcia, M., Marciel Ferreira, J., Ivanov, V., Alexandre, V. & Ferreira, H. Importance of hydraulic strategy trade-offs in structuring response of canopy trees to extreme drought in central Amazon. Oecologia https://doi.org/10.1007/s00442-021-04924-9 (2021).
Ziegler, C. et al. Large hydraulic safety margins protect Neotropical canopy rainforest tree species against hydraulic failure during drought. Ann. For. Sci. 76, 115 (2019).
Fontes, C. G. et al. Convergent evolution of tree hydraulic traits in Amazonian habitats: implications for community assemblage and vulnerability to drought. New Phytol. 228, 106–120 (2020).
Quesada, C. A. et al. Regional and large-scale patterns in Amazon forest structure and function are mediated by variations in soil physical and chemical properties. Biogeosci. Discuss. 6, 3993–4057 (2009).
Johnson, M. O. et al. Variation in stem mortality rates determines patterns of above-ground biomass in Amazonian forests: implications for dynamic global vegetation models. Glob. Change Biol. 22, 3996–4013 (2016).
De Souza, F. C. et al. Evolutionary heritage influences amazon tree ecology. Proc. R. Soc. B 283, 20161587 (2016).
Fauset, S. et al. Hyperdominance in Amazonian forest carbon cycling. Nat. Commun. 6, 6857 (2015).
ForestPlots.net et al. Taking the pulse of Earth’s tropical forests using networks of highly. Biol. Conserv. 260, 108849 (2021).
Peters, J. M. R. et al. Living on the edge: a continental scale assessment of forest vulnerability to drought. Glob. Change Biol. https://doi.org/10.1111/gcb.15641 (2021).
Sanchez-Martinez, P., Martínez-Vilalta, J., Dexter, K. G., Segovia, R. A. & Mencuccini, M. Adaptation and coordinated evolution of plant hydraulic traits. Ecol. Lett. 23, 1599–1610 (2020).
Hammond, W. M. et al. Dead or dying? Quantifying the point of no return from hydraulic failure in drought‐induced tree mortality. New Phytol. https://doi.org/10.1111/nph.15922 (2019).
Costa, F. R. C., Schietti, J., Stark, S. C. & Smith, M. N. The other side of tropical forest drought: do shallow water table regions of Amazonia act as large-scale hydrological refugia from drought? New Phytol. https://doi.org/10.1111/nph.17914 (2022).
Vargas G, G. et al. Beyond leaf habit: generalities in plant function across 97 tropical dry forest tree species. New Phytol. 232, 148–161 (2021).
Esquivel-Muelbert, A. et al. Seasonal drought limits tree species across the Neotropics. Ecography 40, 618–629 (2017).
Brodribb, T. & Hill, R. The importance of xylem constraints in the distribution of conifer species. New Phytol. 143, 365–372 (1999).
Haghtalab, N., Moore, N., Heerspink, B. P. & Hyndman, D. W. Evaluating spatial patterns in precipitation trends across the Amazon basin driven by land cover and global scale forcings. Theor. Appl. Climatol. 140, 411–427 (2020).
Le Quéré, C. et al. Global Carbon Budget 2017. Earth Syst. Sci. Data 10, 405–448 (2018).
Deans, R. M., Brodribb, T. J., Busch, F. A. & Farquhar, G. D. Optimization can provide the fundamental link between leaf photosynthesis, gas exchange and water relations. Nat. Plants 6, 1116–1125 (2020).
B. Eller, C. et al. Xylem hydraulic safety and construction costs determine tropical tree growth. Plant Cell Environ. 41, 548–562 (2018).
Guillemot, J. et al. Small and slow is safe: on the drought tolerance of tropical tree species. Glob. Change Biol. 28, 2622–2638 (2022).
Galbraith, D. et al. Residence times of woody biomass in tropical forests. Plant Ecol. Divers. 6, 139–157 (2013).
Taylor, J. A. & Lloyd, J. Sources and sinks of atmospheric CO2. Aust. J. Bot. 40, 407–418 (1992).
Oliveira, R. S. et al. Linking plant hydraulics and the fast–slow continuum to understand resilience to drought in tropical ecosystems. New Phytol. 230, 904–923 (2021).
Esquivel-Muelbert, A. et al. Tree mode of death and mortality risk factors across Amazon forests. Nat. Commun. 11, 5515 (2020).
Gatti, L. V., Basso, L. S., Miller, J. B. & Gloor, M. Amazonia as a carbon source linked to deforestation and climate change. Nature 595, 388–393 (2021).
Anderegg, W. R. L. et al. Hydraulic diversity of forests regulates ecosystem resilience during drought. Nature 561, 538–541 (2018).
Martínez-Vilalta, J. et al. Towards a statistically robust determination of minimum water potential and hydraulic risk in plants. New Phytol. 232, 404–417 (2021).
Levionnois, S. et al. Vulnerability and hydraulic segmentations at the stem–leaf transition: coordination across Neotropical trees. New Phytol. 228, 512–524 (2020).
Pivovaroff, A. L., Sack, L. & Santiago, L. S. Coordination of stem and leaf hydraulic conductance in southern California shrubs: a test of the hydraulic segmentation hypothesis. New Phytol. 203, 842–850 (2014).
Yoon, J. H. & Zeng, N. An Atlantic influence on Amazon rainfall. Clim. Dynam. 34, 249–264 (2010).
Ciemer, C. et al. Higher resilience to climatic disturbances in tropical vegetation exposed to more variable rainfall. Nat. Geosci. 12, 174–179 (2019).
Chave, J. et al. Improved allometric models to estimate the aboveground biomass of tropical trees. Glob. Change Biol. 20, 3177–3190 (2014).
Huffman, G. J. et al. The TRMM Multisatellite Precipitation Analysis (TMPA): quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 8, 38–55 (2007).
Chave, J. et al. Towards a worldwide wood economics spectrum. Ecol. Lett. 12, 351–366 (2009).
Zanne, A. E. et al. Data from: Towards a worldwide wood economics spectrum. Ecol. Lett. https://doi.org/10.5061/dryad.234 (2009).
Sheil, D., Burslem, D. F. R. P. & Alder, D. The interpretation and misinterpretation of mortality rate measures. J. Ecol. 83, 331–333 (1995).
Araujo-Murakami, A. et al. The productivity, allocation and cycling of carbon in forests at the dry margin of the Amazon forest in Bolivia. Plant Ecol. Divers. 7, 55–69 (2014).
Aragão, L. E. O. C. et al. Spatial patterns and fire response of recent Amazonian droughts. Geophys. Res. Lett. 34, L07701 (2007).
Esquivel-Muelbert, A. et al. Compositional response of Amazon forests to climate change. Glob. Change Biol. https://doi.org/10.1111/gcb.14413 (2018).
Hersbach, H. et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 146, 1999–2049 (2020).
Baker, J. C. A. et al. Evapotranspiration in the Amazon: spatial patterns, seasonality, and recent trends in observations, reanalysis, and climate models. Hydrol. Earth Syst. Sci. 25, 2279–2300 (2021).
Fick, S. E. & Hijmans, R. J. WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 37, 4302–4315 (2017).
Mu, Q., Zhao, M. & Running, S. W. MODIS Global Terrestrial Evapotranspiration (ET) Product (NASA MOD16A2/A3), Algorithm Theoretical Basis Document (NASA, 2013).
Harris, I., Jones, P. D., Osborn, T. J. & Lister, D. H. Updated high-resolution grids of monthly climatic observations—the CRU TS3.10 Dataset. Int. J. Climatol. https://doi.org/10.1002/joc.3711 (2014).
Sperry, J. S., Donnelly, J. R. & Tyree, M. T. A method for measuring hydraulic conductivity and embolism in xylem. Plant. Cell Environ. 11, 35–40 (1988).
Pereira, L. et al. Plant pneumatics: stem air flow is related to embolism—new perspectives on methods in plant hydraulics. New Phytol. 211, 357–370 (2016).
Bittencourt, P., Pereira, L. & Oliveira, R. Pneumatic method to measure plant xylem embolism. Bio-Protocol 8, e3059 (2018).
Paligi, S. S. et al. Accuracy of the pneumatic method for estimating xylem vulnerability to embolism in temperate diffuse-porous tree species. Preprint at BioRxiv https://doi.org/10.1101/2021.02.15.431295. (2021).
Yang, D. et al. A unit pipe pneumatic model to simulate gas kinetics during measurements of embolism in excised angiosperm xylem. Tree Physiol. 43, 88–101 (2023).
Guan, X., Pereira, L., McAdam, S. A. M., Cao, K. F. & Jansen, S. No gas source, no problem: proximity to pre-existing embolism and segmentation affect embolism spreading in angiosperm xylem by gas diffusion. Plant Cell Environ. 44, 1329–1345 (2021).
Zhang, Y. et al. Testing the plant pneumatic method to estimate xylem embolism resistance in stems of temperate trees. Tree Physiol. 38, 1016–1025 (2018).
Sergent, A. S. et al. A comparison of five methods to assess embolism resistance in trees. For. Ecol. Manag. 468, 118175 (2020).
Brum, M. et al. Reconciling discrepancies in measurements of vulnerability to xylem embolism with the pneumatic method: a comment on Chen et al. (2021) ‘Quantifying vulnerability to embolism in tropical trees and lianas using five methods: can discrepancies be explained by xylem structural traits?’. New Phytol. 237, 374–383 (2023).
Pereira, L. & Mazzafera, P. A low cost apparatus for measuring the xylem hydraulic conductance in plants. Bragantia https://doi.org/10.1590/S0006-87052013005000006 (2012).
Chen, Y. J. et al. Quantifying vulnerability to embolism in tropical trees and lianas using five methods: can discrepancies be explained by xylem structural traits? New Phytol. 229, 805–819 (2021).
Pereira, L. et al. Using the pneumatic method to estimate embolism resistance in species with long vessels: a commentary on the article “A comparison of five methods to assess embolism resistance in trees”. For. Ecol. Manag. 479, 2019–2021 (2021).
Pammenter, N. W. & Vander Willigen, C. A mathematical and statistical analysis of the curves illustrating vulnerability of xylem to cavitation. Tree Physiol. 18, 589–593 (1998).
Domec, J. C. & Gartner, B. L. Cavitation and water storage capacity in bole xylem segments of mature and young Douglas-fir trees. Trees Struct. Funct. 15, 204–214 (2001).
Pérez-Harguindeguy, N. et al. Corrigendum to: New handbook for standardised measurement of plant functional traits worldwide. Aust. J. Bot. 64, 715 (2016).
da Costa, A. C. L. et al. Effect of seven years of experimental drought on the aboveground biomass storage of an eastern Amazonian rainforest. New Phytol. 187, 579–591 (2010).
Lopez-Gonzalez, G., Lewis, S. L., Burkitt, M., Baker, T. R. & Phillips, O. L. ForestPlots.net Database (ForestPlots, accessed 1 September 2018); www.forestplots.net.
Lopez-Gonzalez, G., Lewis, S. L., Burkitt, M. & Phillips, O. L. ForestPlots.net: a web application and research tool to manage and analyse tropical forest plot data. J. Veg. Sci. https://doi.org/10.1111/j.1654-1103.2011.01312.x (2011).
Sullivan, M. J. P. et al. Long-term thermal sensitivity of Earth’s tropical forests. Science 368, 869–874 (2020).
Talbot, J. et al. Methods to estimate aboveground wood productivity from long-term forest inventory plots. For. Ecol. Manag. 320, 30–38 (2014).
Lewis, S. L. et al. Tropical forest tree mortality, recruitment and turnover rates: calculation, interpretation and comparison when census intervals vary. J. Ecol. 92, 929–944 (2004).
Lopez‐Gonzalez, G., Sullivan, M. J. P. & Baker, T. R. BiomasaFP: Tools for analysing data downloaded from ForestPlots.net. R package version 1 (2015).
Guevara, J. E. et al. Low phylogenetic beta diversity and geographic neo-endemism in Amazonian white-sand forests. Biotropica 48, 34–46 (2016).
Warton, D. I., Duursma, R. A., Falster, D. S. & Taskinen, S. smatr 3—an R package for estimation and inference about allometric lines. Methods Ecol. Evol. 3, 257–259 (2012).
RStudio Team. RStudio: Integrated Development for R (RStudio, 2016).
Acknowledgements
Data collection was largely funded by the UK Natural Environment Research Council (NERC) project TREMOR (NE/N004655/1) to D.G., E.G. and O.P., with further funds from Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES, finance code 001) to J.V.T. and a University of Leeds Climate Research Bursary Fund to J.V.T. D.G., E.G. and O.P. acknowledge further support from a NERC-funded consortium award (ARBOLES, NE/S011811/1). This paper is an outcome of J.V.T.’s doctoral thesis, which was sponsored by CAPES (GDE 99999.001293/2015-00). J.V.T. was previously supported by the NERC-funded ARBOLES project (NE/S011811/1) and is supported at present by the Swedish Research Council Vetenskapsrådet (grant no. 2019-03758 to R.M.). E.G., O.P. and D.G. acknowledge support from NERC-funded BIORED grant (NE/N012542/1). O.P. acknowledges support from an ERC Advanced Grant and a Royal Society Wolfson Research Merit Award. R.S.O. was supported by a CNPq productivity scholarship, the São Paulo Research Foundation (FAPESP-Microsoft 11/52072-0) and the US Department of Energy, project GoAmazon (FAPESP 2013/50531-2). M.M. acknowledges support from MINECO FUN2FUN (CGL2013-46808-R) and DRESS (CGL2017-89149-C2-1-R). C.S.-M., F.B.V. and P.R.L.B. were financed by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brasil (CAPES, finance code 001). C.S.-M. received a scholarship from the Brazilian National Council for Scientific and Technological Development (CNPq 140353/2017-8) and CAPES (science without borders 88881.135316/2016-01). Y.M. acknowledges the Gordon and Betty Moore Foundation and ERC Advanced Investigator Grant (GEM-TRAITS, 321131) for supporting the Global Ecosystems Monitoring (GEM) network (gem.tropicalforests.ox.ac.uk), within which some of the field sites (KEN, TAM and ALP) are nested. We thank Brazil–USA Collaborative Research GoAmazon DOE-FAPESP-FAPEAM (FAPESP 2013/50533-5 to L.A.) and National Science Foundation (award DEB-1753973 to L. Alves). We thank Serrapilheira Serra-1709-18983 (to M.H.) and CNPq-PELD/POPA-441443/2016-8 (to L.G.) (P.I. Albertina Lima). We thank all the colleagues and grants mentioned elsewhere8,36 that established, identified and measured the Amazon forest plots in the RAINFOR network analysed here. We particularly thank J. Lyod, S. Almeida, F. Brown, B. Vicenti, N. Silva and L. Alves. This work is an outcome approved Research Project no. 19 from ForestPlots.net, a collaborative initiative developed at the University of Leeds that unites researchers and the monitoring of their permanent plots from the world’s tropical forests61. We thank A. Levesley, K. Melgaço Ladvocat and G. Pickavance for ForestPlots.net management. We thank Y. Wang and J. Baker, respectively, for their help with the map and with the climatic data. We acknowledge the invaluable help of M. Brum for kindly providing the comparison of vulnerability curves based on PAD and on PLC shown in this manuscript. We thank J. Martinez-Vilalta for his comments on an early version of this manuscript. We also thank V. Hilares and the Asociación para la Investigación y Desarrollo Integral (AIDER, Puerto Maldonado, Peru); V. Saldaña and Instituto de Investigaciones de la Amazonía Peruana (IIAP) for local field campaign support in Peru; E. Chavez and Noel Kempff Natural History Museum for local field campaign support in Bolivia; ICMBio, INPA/NAPPA/LBA COOMFLONA (Cooperativa mista da Flona Tapajós) and T. I. Bragança-Marituba for the research support. We warmly thank the tree climbers H. Ninantay, A. Ninantay, Adenor da Silva Lima, Adrinao da Silva Lima, J. Caruta, Adriano, Kelvin and Graveto.
Funding
Open access funding provided by Uppsala University.
Author information
Authors and Affiliations
Contributions
J.V.T., D.G. and E.G. designed the study with inputs from R.S.O., M.M. and O.P. Data analysis was by J.V.T. with inputs from D.G., E.G., O.P., M.M., R.S.O., L.P. and A.E.-M. The manuscript was written by J.V.T. and D.G. with inputs from E.G., R.S.O., M.M., O.P., L.P., P.B., F.d.V.B., A.E.-M., L.R., P.M., Y.M., P.M., R.B., M.D., M.C.S., M.H., H.J., L.G., B.S.M., I.O.M., B.H.M.J., W.C. and E.H. All field campaigns in the western Amazon were led by J.V.T. and C.S.-M. and co-led by F.C.D. and M.G. Data for the western Amazon were collected by M.J.M.Z., C.A.S.Y., M.A., F.M.P.M., A.N., J.M.B.S., J.S.T., R.S.C.C., J.B., L.F., E.R.M.C., J.A.R.S., R.T., L.T., M.T.M.U., G.A.C. and F.M. Data collection and analysis for the southern Amazon was led by H.J. and M.C.S. under supervision of B.S.M., I.O.M. and B.H.M.J. The LMA data from the southern Amazon were collected and analysed by W.J.A.C. M.F. and A.C.-O. measured leaf area and calculated LMA data for the western Amazon forest. D.P., M.C.R., M. Schlickmann. and G.R. collected and analysed LMA data for Tapajós forest under the supervision of M.H. and L.G. Forest dynamics data were collected or managed by O.P., Y.M., A.A.-M., E.A., J.d.A.P., L.A., T.R.B., P.B.C., R.B., W.C., S.C.R., F.C.S., E.C. N.D.C., R.d.C.S., M.D., J.S.E., T.F., L.F., N.H., E.H., W.H.H., S.L., G.F.L., A.M.M., P.M., V.C.M., R.M., A.R.R., N.S., M. Silveira., J.T., R.V., L.V., S.L., S.A.V. and A.C.L.C. All authors critically revised the manuscript and gave final approval for publication.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Timothy Brodribb, Martyna Kotowska, Eduardo Maeda and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Precipitation regimes of sampled sites.
Precipitation data were obtained from TRMM (the Tropical Rainfall Measuring Mission—TMPA/3B43 version 7)64 at 0.25o spatial resolution from 1998–2016. Maximum cumulative water deficit (MCWD) was computed following Aragão et al. (2007) but replacing universal ET values with site-specific values derived from the ERA-5 re-analysis product71. MCWD is defined as the maximum climatologically-induced water deficit (see equation 1 in Methods). Sites in which MCWD~0 do not experience seasonality (dry season length (DSL) = 0), while sites with very negative MCWD values are strongly seasonally water-stressed. Sites are colour-coded by forest types, based on their seasonal rainfall patterns: aseasonal (blue), intermediate DSL (green) and long DSL (brown).
Extended Data Fig. 2 Climatological data corresponding to Ψdry (in situ dry season leaf water potential) sampling at each site.
Grey bars and error bars show the mean and standard deviation of monthly precipitation from 1991 to 2018 (CRU data ts.4.0338)75. The blue dashed lines represent the year of sampling, while the brown points show the months at which \(\varPsi \)dry was measured. Hydraulic traits and climatic data for TAP were obtained from Brum et al.27. We display CRU data in this figure due to no availability of TRMM (Tropical Rainfall Measuring Mission) data beyond 2016. Sampling years can be found in Supplementary Table 8.
Extended Data Fig. 3 Functional trait range of species sampled in this study.
Histograms of life-history related traits of the sampled species (red) in relation to comprehensive histograms of the broader Amazon tree flora (grey). A) Mean wood density (g cm−3)65,66; Potential size, calculated as the 95th percentile of diameter distribution (cm); C) Maximum growth, calculated as the 95th percentile of individual growth rates available for a given species (cm yr−1); D) Mean growth rate (cm yr−1); E) Mean mortality rate (% yr−1). All trait data shown in this figure were extracted from Coelho de Souza et al.37.
Extended Data Fig. 4 Hydraulic traits variation at species and community level.
Top panels: variation in hydraulic traits across Amazon forest types; long DSL (brown), intermediate DSL (green) and aseasonal (blue). A) xylem water potential at which 50% (\(\varPsi \)50) of the conductance is lost. B) hydraulic safety margins related to \(\varPsi \)50 (HSM50 = \(\varPsi \)dry – \(\varPsi \)50). C) minimum leaf water potential observed in the dry season (\(\varPsi \)dry). Dashed lines show the mean value of each trait across all tree taxa. Red lines denote hydraulic safety margins equal to zero. Significant differences at p < 0.05 are shown by letters above each boxplot (Kruskal–Wallis followed by post hoc Mann–Whitney–Wilcoxon Rank Sum test). Each point represents one species per site. Long DSL, intermediate DSL and aseasonal forests encompass 3, 5 and 3 forest sites, respectively. Boxplots display the 25th percentile, median and 75th percentile. The vertical bars show the interquartile range times 1.5 and datapoints beyond these bars are outliers. Bottom panels: Relationship between tree basal-area weighted mean hydraulic traits and maximum cumulative water deficit (MCWD). D) Basal area-weighted mean \(\psi \)50 (xylem water potential at which 50% of the conductance is lost); E) Basal area-weighted mean hydraulic safety margin (HSM50); F) Basal area-weighted mean minimum leaf water potential observed in the dry season (\(\varPsi \)dry); n = 11 sites. Significant linear relations are shown by regression lines and 95% confidence intervals, by shaded areas. See methods for MCWD calculations.
Extended Data Fig. 5 Leaf habit information of the sampled species per plot (top panels), hydraulic trait variation across leaf habit groups (middle panels) and relationship between basal area-weighted mean hydraulic traits and maximum cumulative water deficit when excluding deciduous and semideciduous species.
A) and D) xylem water potential at which 50% of the conductance is lost (\(\varPsi \)50); B) and E) Hydraulic safety margins related to \(\varPsi \)50 (HSM50 = \(\varPsi \)dry – \(\varPsi \)50 and C) and F) Minimum in situ leaf water potential observed in the dry season (\(\varPsi \) dry). Dashed lines denote the mean value of each trait across all tree taxa in the dataset. Red line, the hydraulic safety margins equal to zero. Boxplots display the 25th percentile, median and 75th percentile. The vertical bars show the interquartile range times 1.5 and datapoints beyond these bars are outliers. Sites are sorted by increasing water availability. Each point represents one species per site (N = 170 species) in the top panels and species mean (\(\varPsi \)50, HSM50) and species minimum \(\varPsi \)dry per leaf habit in the bottom panels (N = 136 species). Deciduous, semideciduous and evergreen species are represented by red, blue and green points, respectively. Grey points or NA represent species for which leaf habit information was not available. Significant differences at p < 0.05 are represented by different letters above each boxplot (Kruskal–Wallis followed by post hoc Mann–Whitney–Wilcoxon Rank Sum test). G) \(\psi \)50 (xylem water potential on which 50% of the conductance is lost; H) Hydraulic safety margin (HSM50 = \(\varPsi \)dry – \(\varPsi \)50); I) In situ leaf water potential observed in the dry season (\(\varPsi \) dry); n = 10 sites. Significant linear relations are shown by regression lines. The shaded area represents the 95% confidence interval of the regression slope. Further leaf habit information of sampled species is provided in Supplementary Table 10.
Extended Data Fig. 6 Bivariate relationship between plot relative aboveground net biomass change (ΔAGB) and basal-area-weighted mean vegetation traits (A–E) and climatic variables (F–I) across Amazonian forest plots.
Due to high standing aboveground biomass variability across sites, we computed relative ΔAGB values as: ((AGB end – AGB start)/census length)/AGB (time-weighted mean standing woody biomass). Each point indicates a forest plot. Information about each plot and the observation period used can be found in Supplementary Table 5. Stem wood density data were extracted from the Global Wood Density database65,66. KEN plots were excluded from all forest dynamics analyses because of a fire event that occurred in the region in 200466 and may still be affecting biomass accrual. Regression lines show significant relationships using standard major axis (SMA) models after Bonferroni correction for multiples hypothesis testing. Supplementary Table 3 shows the results of the SMA models.
Extended Data Fig. 7 Plot-level analyses: bivariate relationships between basal area-weighted mean hydraulic safety margin and forest dynamics across Amazonian forest plots.
Basal area-weighted mean HSM50 in relation to relative (A-C) and absolute (D-H) forest dynamics values. A) Relative annual aboveground biomass net change (ΔAGB/AGB), where: ΔAGB is the difference in aboveground biomass between the final and initial censuses (AGBfinal census – AGBinitial census) divided by total monitoring length for that plot (Datefinal census – Dateinitial census) in years and AGB is the time-weighted mean standing woody biomass across censuses per plot; B) Relative annual mortality in terms of biomass: (AGBMORT/AGB). Where AGBMORT is the sum of the AGB of all dead trees and the unobserved components (see methods), divided by the census interval length95;C) Relative annual AGB wood productivity: (AGWP/AGB), where AGWP is defined as the sum of the biomass growth of surviving trees >10 cm DBH, new recruits > 10 cm DBH and the unobserved components (see methods), within a plot in a given census interval, divided by the census interval length95; D) Annual aboveground biomass net change (ΔAGB); E) Annual aboveground biomass mortality (AGBMORT); F) Annual aboveground wood productivity (AGWP), G) Annual instantaneous stem mortality rate (See methods Equation 4)67; H) Residence time of woody biomass calculated as the ratio of mean standing biomass to mean biomass mortality rate52. All these parameters were calculated for each census interval and we calculated time-weighted mean to have one value per plot. Each point indicates one forest plot. Significant linear relations are shown by regression lines (Standard major axis models). The shade area represents the 95% bootstrapped confidence interval. Information about each plot and the observation period is available on Supplementary Table 5. Supplementary Table 4 shows the results of the SMA models.
Extended Data Fig. 8 Cluster-level analyses: Relationship between basal area weighted mean HSM50 and cluster mean forest dynamics across clusters of forest plots.
Basal area-weighted mean HSM50 in relation to cluster mean relative (A–C) and absolute (D–H) forest dynamics values. A) Relative annual aboveground biomass net change (ΔAGB/AGB), where: ΔAGB is the difference in aboveground biomass between the final and initial censuses (AGBfinal census – AGBinitial census) divided by total monitoring length for that plot (Datefinal census – Dateinitial census) in years and AGB is the time-weighted mean standing woody biomass across censuses per plot; B) Relative annual mortality in terms of biomass: (AGBMORT/AGB). Where AGBMORT is the sum of the AGB of all dead trees and the unobserved components (see methods), divided by the census interval length95;C) Relative annual AGB wood productivity: (AGWP/AGB), where AGWP is defined as the sum of the biomass growth of surviving trees >10 cm DBH, new recruits > 10 cm DBH and the unobserved components (see methods), within a plot in a given census interval, divided by the census interval length95; D) Annual aboveground biomass net change (ΔAGB); E) Annual aboveground biomass mortality (AGBMORT); F) Annual aboveground wood productivity (AGWP), G) Annual instantaneous stem mortality rate (see methods)67; H) Residence time of woody biomass calculated as the ratio of mean standing biomass to mean biomass mortality rate52. All these parameters were calculated for each census interval and we calculated time-weighted mean to have one value per plot. Each point indicates the mean value across clusters of forest plots, which in total encompass 31.37 ha of forest spread across 34 plots. Information about each cluster and the observation period used for each cluster is provided in Supplementary Table 5. The solid line is the best fit line of the standard major axis (SMA) model and the shaded area represents the 95% bootstrapped confidence interval. Supplementary Table 4 shows the results of the SMA models.
Extended Data Fig. 9 Relationship between published pan-Amazonian species-level growth rates37 and hydraulic safety margins.
We restrict our analysis to the western Amazon, where there is the highest overlap of species between ours and Coelho de Souza et al.37 dataset and to avoid biases due to soil/forest dynamic differences across Amazonian regions. Hydraulic safety margins for species occurring across multiple sites were averaged to yield one value per species.
Extended Data Fig. 10 HSM5Plot-level analyses: bivariate relationships between basal area-weighted mean HSM88 and forest dynamics across Amazonian forest plots.
Basal area-weighted mean HSM88 in relation to relative (A-C) and absolute (D-H) forest dynamics values. A) Relative annual aboveground biomass net change (ΔAGB/AGB), where: ΔAGB is the difference in aboveground biomass between the final and initial censuses (AGBfinal census – AGBinitial census) divided by total monitoring length for that plot (Datefinal census – Dateinitial census) in years and AGB is the time-weighted mean standing woody biomass across censuses per plot; B) Relative annual mortality in terms of biomass: (AGBMORT/AGB). Where AGBMORT is the sum of the AGB of all dead trees and the unobserved components (see methods), divided by the census interval length95;C) Relative annual AGB wood productivity: (AGWP/AGB), where AGWP is defined as the sum of the biomass growth of surviving trees >10 cm DBH, new recruits > 10 cm DBH and the unobserved components (see methods), within a plot in a given census interval, divided by the census interval length95; D) Annual aboveground biomass net change (ΔAGB); E) Annual aboveground biomass mortality (AGBMORT); F) Annual aboveground wood productivity (AGWP), G) Annual instantaneous stem mortality rate (see methods Equation 4)67; H) Residence time of woody biomass calculated as the ratio of mean standing biomass to mean biomass mortality rate52. All these parameters were calculated for each census interval and we calculated time-weighted mean to have one value per plot. Each point indicates one forest plot. Significant linear relations are shown by regression lines (Standard major axis models). The shade area represents the 95% bootstrapped confidence interval. Information about each plot and the observation period is available on Supplementary Table 5. Supplementary Table 4 shows the results of the SMA models.
Supplementary information
Supplementary Tables
Supplementary Tables 1–10.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tavares, J.V., Oliveira, R.S., Mencuccini, M. et al. Basin-wide variation in tree hydraulic safety margins predicts the carbon balance of Amazon forests. Nature 617, 111–117 (2023). https://doi.org/10.1038/s41586-023-05971-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-023-05971-3
This article is cited by
-
Amazon forest biogeography predicts resilience and vulnerability to drought
Nature (2024)
-
Critical transitions in the Amazon forest system
Nature (2024)
-
Impact of the 2015–2016 El Niño on the carbon dynamics of South American tropical forests
Nature Climate Change (2023)
-
Increased hydraulic risk in assemblages of woody plant species predicts spatial patterns of drought-induced mortality
Nature Ecology & Evolution (2023)
-
Tree hydrological niche acclimation through ontogeny in a seasonal Amazon forest
Plant Ecology (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.