Abstract
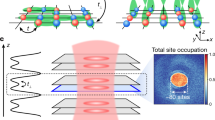
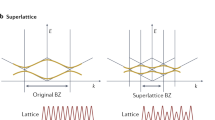
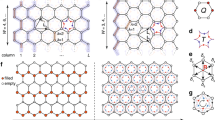
Observation of strong correlations and superconductivity in twisted-bilayer graphene1,2,3,4 has stimulated tremendous interest in fundamental and applied physics5,6,7,8. In this system, the superposition of two twisted honeycomb lattices, generating a moiré pattern, is the key to the observed flat electronic bands, slow electron velocity and large density of states9,10,11,12. Extension of the twisted-bilayer system to new configurations is highly desired, which can provide exciting prospects to investigate twistronics beyond bilayer graphene. Here we demonstrate a quantum simulation of superfluid to Mott insulator transition in twisted-bilayer square lattices based on atomic Bose–Einstein condensates loaded into spin-dependent optical lattices. The lattices are made of two sets of laser beams that independently address atoms in different spin states, which form the synthetic dimension accommodating the two layers. The interlayer coupling is highly controllable by a microwave field, which enables the occurrence of a lowest flat band and new correlated phases in the strong coupling limit. We directly observe the spatial moiré pattern and the momentum diffraction, which confirm the presence of two forms of superfluid and a modified superfluid to insulator transition in twisted-bilayer lattices. Our scheme is generic and can be applied to different lattice geometries and for both boson and fermion systems. This opens up a new direction for exploring moiré physics in ultracold atoms with highly controllable optical lattices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
All data generated or analysed during this study are included in this published article. Further data are also available from the corresponding authors upon reasonable request.
References
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Wang, J., Mu, X., Wang, L. & Sun, M. Properties and applications of new superlattice: twisted bilayer graphene. Mater. Today Phys. 9, 100099 (2019).
Andrei, E. Y. & MacDonald, A. H. Graphene bilayers with a twist. Nat. Mater. 19, 1265–1275 (2020).
Balents, L., Dean, C. R., Efetov, D. K. & Young, A. F. Superconductivity and strong correlations in Moiré flat bands. Nat. Phys. 16, 725–733 (2020).
Kennes, D. M. et al. Moiré heterostructures as a condensed-matter quantum simulator. Nat. Phys. 17, 155–163 (2021).
Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Graphene bilayer with a twist: electronic structure. Phys. Rev. Lett. 99, 256802 (2007).
Mele, E. J. Commensuration and interlayer coherence in twisted bilayer graphene. Phys. Rev. B 81, 161405 (2010).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Moon, P. & Koshino, M. Energy spectrum and quantum Hall effect in twisted bilayer graphene. Phys. Rev. B 85, 195458 (2012).
Wang, P. et al. Localization and delocalization of light in photonic moiré lattices. Nature 577, 42–46 (2020).
Huang, C. et al. Localization-delocalization wavepacket transition in Pythagorean aperiodic potentials. Sci. Rep. 6, 32546 (2016).
Fu, Q. et al. Optical soliton formation controlled by angle twisting in photonic Moiré lattices. Nat. Photon. 14, 663–668 (2020).
Hu, G. et al. Topological polaritons and photonic magic angles in twisted α-MoO3 bilayers. Nature 582, 209–213 (2020).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Lewenstein, M., Sanpera, A. & Ahufinger, V. Ultracold Atoms in Optical Lattices: Simulating Quantum Many-Body systems (Oxford Univ. Press, 2012).
Windpassinger, P. & Sengstock, K. Engineering novel optical lattices. Rep. Prog. Phys. 76, 086401 (2013).
Soltan-Panahi, P. et al. Multi-component quantum gases in spin-dependent hexagonal lattices. Nat. Phys. 7, 434–440 (2011).
Wirth, G., Ölschläger, M. & Hemmerich, A. Evidence for orbital superfluidity in the P-band of a bipartite optical square lattice. Nat. Phys. 7, 147–153 (2011).
Tarruell, L., Greif, D., Uehlinger, T., Jotzu, G. & Esslinger, T. Creating, moving and merging Dirac points with a Fermi gas in a tunable honeycomb lattice. Nature 483, 302–305 (2012).
Jo, G. B. et al. Ultracold atoms in a tunable optical kagome lattice. Phys. Rev. Lett. 108, 045305 (2012).
Taie, S. et al. Coherent driving and freezing of bosonic matter wave in an optical Lieb lattice. Sci. Adv. 1, e1500854 (2015).
Gall, M., Wurz, N., Samland, J., Chan, C. F. & Köhl, M. Competing magnetic orders in a bilayer Hubbard model with ultracold atoms. Nature 589, 40 (2021).
González-Tudela, A. & Cirac, J. I. Cold atoms in twisted-bilayer optical potentials. Phys. Rev. A 100, 053604 (2019).
Luo, X. & Zhang, C. Spin-twisted optical lattices: tunable flat bands and Larkin-Ovchinnikov superfluids. Phys. Rev. Lett. 126, 103201 (2021).
Graß, T., Chhajlany, R. W., Tarruell, L., Pellegrini, V. & Lewenstein, M. Proximity effects in cold atom artificial graphene. 2D Mater. 4, 015039 (2016).
Salamon, T. et al. Simulating twistronics without a twist. Phys. Rev. Lett. 125, 030504 (2020).
Boada, O., Celi, A., Latorre, J. I. & Lewenstein, M. Quantum simulation of an extra dimension. Phys. Rev. Lett. 108, 133001 (2012).
Celi, A. et al. Synthetic gauge fields in synthetic dimensions. Phys. Rev. Lett. 112, 043001 (2014).
Ozawa, T. & Price, H. M. Topological quantum matter in synthetic dimensions. Nat. Rev. Phys. 1, 349–357 (2019).
LeBlanc, L. J. & Thywissen, J. H. Species-specific optical lattices. Phys. Rev. A 75, 053612 (2007).
Arora, B., Safronova, M. S. & Clark, C. W. Tune-out wavelengths of alkali-metal atoms and their applications. Phys. Rev. A 84, 043401 (2011).
Wen, K. et al. Experimental study of tune-out wavelengths for spin-dependent optical lattice in 87Rb Bose-Einstein condensation. J. Opt. Soc. Am. B 38, 3269 (2021).
McDonald, M., Trisnadi, J., Yao, K. & Chin, C. Superresolution microscopy of cold atoms in an optical lattice. Phys. Rev. X 9, 021001 (2019).
Gerbier, F. et al. Interference pattern and visibility of a Mott insulator. Phys. Rev. A 72, 053606 (2005).
Fisher, M. P. A., Weichman, P. B., Grinstein, G. & Fisher, D. S. Boson localization and the superfluid-insulator transition. Phys. Rev. B 40, 546–570 (1989).
Krauth, W., Trivedi, N. & Ceperley, D. Superfluid-insulator transition in disordered boson systems. Phys. Rev. Lett. 67, 2307–2310 (1991).
Freericks, J. K. & Monien, H. Strong-coupling expansions for the pure and disordered Bose-Hubbard model. Phys. Rev. B 53, 2691–2700 (1996).
Kariyado, T. & Vishwanath, A. Flat band in twisted bilayer Bravais lattices. Phys. Rev. Res. 1, 033076 (2019).
Kennes, D. M., Xian, L., Claassen, M. & Rubio, A. One-dimensional flat bands in twisted bilayer germanium selenide. Nat. Commun. 11, 31124 (2020).
Xiong, D., Wang, P., Fu, Z., Chai, S. & Zhang, J. Evaporative cooling of 87Rb atoms into Bose-Einstein condensate in an optical dipole trap. Chin. Opt. Lett. 8, 627–629 (2010).
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39 (2002).
Steck, D. A. Quantum and Atom Optics https://atomoptics.uoregon.edu/~dsteck/teaching/quantum-optics/ (2007).
Zwerger, W. Mott Hubbard transition of cold atoms in optical lattices. J. Opt. B: Quantum Semiclass. Opt. 5, S9–S16 (2003).
Krauth, W., Caffarel, M. & Bouchaud, J. P. Gutzwiller wave function for a model of strongly interacting bosons. Phys. Rev. B 45, 3137–3140 (1992).
Sheshadri, K., Krishnamurthy, H. R., Pandit, R. & Ramakrishnan, T. V. Superfluid and insulating phases in an interacting-Boson model: mean-field theory and the RPA. Europhys. Lett. 22, 257–263 (1993).
Jaksch, D., Bruder, C., Cirac, J. I., Gardiner, C. W. & Zoller, P. Cold Bosonic atoms in optical lattices. Phys. Rev. Lett. 81, 3108–3111 (1998).
Acknowledgements
This research is supported by Innovation Program for Quantum Science and Technology (grant no. 2021ZD0302003), National Key Research and Development Program of China (grant nos. 2016YFA0301602, 2018YFA0307601 and 2022YFA1404101), NSFC (grant nos. 12034011, 12022406, 12074342 and 11804203), the Fund for Shanxi ‘1331 Project’ Key Subjects Construction and Tencent (Xplorer Prize). C.C. acknowledges support by the National Science Foundation (grant no. PHY-2103542) and the Army Research Office STIR (grant no. W911NF2110108).
Author information
Authors and Affiliations
Contributions
J.Z. conceived the idea and performed the experimental designs. L.W., Z.M., F.L., K.W., P.W. and J.Z. performed the experiments. C.C., Z.M., L.W., F.L., W.H. and J.Z. analysed the data and all authors discussed the results. W.H., C.G. and J.Z. performed the simulation. Z.M. plotted the figures. J.Z. and C.C. wrote the manuscript. All authors interpreted the results and reviewed the manuscript. J.Z. designed and supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Richard Schmidt and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Extended data
is available for this paper at https://doi.org/10.1038/s41586-023-05695-4.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Coherence in the SF-MI transition.
a, The initial BEC in 2D pancake-like potential. b, Absorption image after atoms are released abruptly from an optical lattice potential V1 (or V2) with a potential depth 24Er. c, Absorption image when the lattice is ramped up to the lattice depth 24Er and then ramp down to zero. The images are obtained after 18 ms free space expansion.
Extended Data Fig. 2 Determination of tune-out wavelengths.
a–b, The lattice depth V1x (blue) and V1y (red) as a function of wavelength λ for the two different hyperfine states \(\left|F=1,{m}_{F}=1\right\rangle \) and \(\left|F=2,{m}_{F}=0\right\rangle \). The angles between V1x, V1y and B0 are 39.79° and 50.21° respectively. c–d, The potential depth V2x (blue) and V2y (red) as a function of wavelength λ for the two different hyperfine states \(\left|F=1,{m}_{F}=1\right\rangle \) and \(\left|F=2,{m}_{F}=0\right\rangle \). e, Theoretical light shift of V1x, V1y for \(\left|1,1\right\rangle \) and \(\left|2,0\right\rangle \). f, Theoretical lattice depth of V2x, V2y for \(\left|1,1\right\rangle \) and \(\left|2,0\right\rangle \). The bias magnetic field of 10 Gauss is applied along the 45° diagonal line of the square lattice V2.
Extended Data Fig. 3 Band structure of the twisted-bilayer optical lattices.
The twist angle of the commensurate optical lattice is \(\theta =2\,\arctan \,(1/22)\), whose band structure is regarded as an approximation of the experimental case θ = 5.21°. a, b and c show the band structures for the interlayer coupling strength ΩR = 0Er, 0.1Er and 1Er respectively. a also gives the band structure without the interlayer coupling in the form of the superlattice minibands within the same reduced Brillouin zone. d,e and f are the enlargement of the lowest bands of a,b, and c, respectively. g,h and i are the further enlargement of the lowest bands of d,e and f, respectively. Here, the MW detuning is Δ = 0, V0= 4Er and E0 corresponds to the energy of the lowest band.
Extended Data Fig. 4 Characteristics of the different phases.
a, Phase diagram, where SF, SF-II, MI, and I refer to superfluid, superfluid only with short-range coherence, Mott insulator, and insulator. b, Table shows the features of the different phases. c, Plots of the order parameter \(\langle {\hat{b}}_{i}\rangle \) and the filling of the atoms on the site n for the different phases. Parameters (V/Er, ΩR/Er) are (10,0.6), (15,0.6), (23,0.3) and (23,1.1) for the plots from left to right respectively. The chemical potential μ/U = 1 is considered.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Meng, Z., Wang, L., Han, W. et al. Atomic Bose–Einstein condensate in twisted-bilayer optical lattices. Nature 615, 231–236 (2023). https://doi.org/10.1038/s41586-023-05695-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-023-05695-4
This article is cited by
-
Two-dimensional localized modes in nonlinear systems with linear nonlocality and moiré lattices
Frontiers of Physics (2024)
-
Quasiperiodic circuit quantum electrodynamics
npj Quantum Information (2023)
-
Reconfigurable moiré nanolaser arrays with phase synchronization
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.