Abstract
Thwaites Glacier represents 15% of the ice discharge from the West Antarctic Ice Sheet and influences a wider catchment1,2,3. Because it is grounded below sea level4,5, Thwaites Glacier is thought to be susceptible to runaway retreat triggered at the grounding line (GL) at which the glacier reaches the ocean6,7. Recent ice-flow acceleration2,8 and retreat of the ice front8,9,10 and GL11,12 indicate that ice loss will continue. The relative impacts of mechanisms underlying recent retreat are however uncertain. Here we show sustained GL retreat from at least 2011 to 2020 and resolve mechanisms of ice-shelf melt at the submetre scale. Our conclusions are based on observations of the Thwaites Eastern Ice Shelf (TEIS) from an underwater vehicle, extending from the GL to 3 km oceanward and from the ice–ocean interface to the sea floor. These observations show a rough ice base above a sea floor sloping upward towards the GL and an ocean cavity in which the warmest water exceeds 2 °C above freezing. Data closest to the ice base show that enhanced melting occurs along sloped surfaces that initiate near the GL and evolve into steep-sided terraces. This pronounced melting along steep ice faces, including in crevasses, produces stratification that suppresses melt along flat interfaces. These data imply that slope-dependent melting sculpts the ice base and acts as an important response to ocean warming.
Similar content being viewed by others
Main
Offshore ocean and atmospheric conditions force warm circumpolar deep water (CDW) onto the Amundsen Sea continental shelf13,14, where it contributes to ice loss and GL retreat of glaciers draining this sector of the West Antarctic Ice Sheet, including Thwaites Glacier11. Thwaites Glacier extends seaward from the Walgreen Coast, forming the Thwaites Glacier Tongue (TGT) to the west and the TEIS that rests on a prominent sea-floor pinning point (Fig. 1a). Warm CDW flows towards the glacier along the coastline and through sea-floor channels15,16,17, where it drives melting. The bed underneath the upstream grounded ice deepens to a maximum of 2,300 m below sea level4,5, making it susceptible to large-scale retreat from ocean-driven melting7. Collapse of Thwaites Glacier, which itself represents more than half a metre of global sea-level-rise potential, could also destabilize neighbouring glaciers that account for a further 3 m of future sea level rise4.
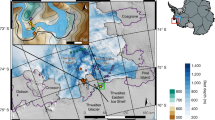
a, Historical GL positions (coloured lines/zones after ref. 12) demonstrate notable GL retreat over the past two decades (QGIS map: Landsat 8, 15 m pixel−1, band 8 image LC08_L1GT_003113_20200131_20200211_01_T2_B8, 31 January 2020; the red box denotes the study region). b,c, Warm water is delivered close to the ice base (upper grey regions), shown by contours of thermal driving (degrees above in situ freezing point). The ice (black line) and seabed (brown regions) elevation profiles are measured by up and down altimetry from Icefin, which compare with bathymetry from mapping and forward sonar (Fig. 2). The small circles denote the Icefin track, along two transects approaching the GL, T1 (red) and T2 (blue) shown in the lower inset (red box from a). The yellow circle in the inset and vertical line through the ice denote the location of the borehole. The T1 track is oriented 5–10° oblique to the flow direction of the glacier and T2 approximately 50° oblique to flow; Icefin reached the grounded point of the glacier at the end of T2. Triangles in b and c mark historic GL locations estimated from satellite interferometry for 2011 (white), and the furthest downstream estimate in 2016 (blue)12. In b, the yellow triangle denotes the potential GL wedge detected by Icefin (Fig. 2). Nearest to the GL, although temperatures are colder than the deep water, the ocean water holds more than one degree of thermal driving. The ice base transitions from rough near the GL to terraced (progressively steeper-sided step-like features) near and downstream of the borehole, suggestive of progressive melting. Crevasses also contain terraces, especially clear in c.
Changes in the Thwaites system have accelerated over the past 20 years (refs. 8,9,10), resulting in breakup of the TGT and propagation of rifts across the TEIS10. Recent GL retreat has varied from 0.6 to 1.2 km year−1 (ref. 12). Ocean melting, dynamic thinning and ice-flow rates influence this retreat12, but exactly how these factors operate is difficult to constrain with generally poor observations below the ice. Satellite observations, which measure the surface elevation of the glacier, suggest that the TEIS is thinning on average 25 metres per decade10,12, whereas airborne ice-penetrating radar that directly measures ice thickness estimates rates up to 45 metres per decade18.
Although ocean-driven melting directly influences the stability of ice around Antarctica19,20, little data resolve the interaction between the ice and ocean directly21,22,23,24,25,26,27,28,29,30. Models of ocean forcing are often limited by resolution or available parameterizations. Generally, models represent ice shelves simplistically as wedges of ice with flat or curved interfaces and an inferred sea-floor geometry as a function of distance from the presumed GL. Usually a zero-melt condition is imposed at the GL31, which is inconsistent with evidence of thinning and GL retreat. Although retrograde bed slopes facilitate positive feedback in grounded ice loss from ocean-forced melt6,7, glaciers resting on prograde slopes still face influence from warm water undercutting the ice. Temperature and salinity variations influence circulation and heat exchange between the ice and ocean. These variations occur at scales much smaller than those resolved by remote sensing or captured in ice-shelf-wide models of ice–ocean interactions. Furthermore, few direct measurements have been made near the ice base24,25,26,27,28,29,30, and none at the GL of a considerable glacier, that would help models at large and small scales better represent melting. Therefore, how melting occurs under ice shelves and particularly at the GL, influencing ice loss, remains largely unresolved.
As part of the National Science Foundation (NSF)-Natural Environment Research Council (NERC) International Thwaites Glacier Collaboration (ITGC), a comprehensive field campaign was carried out over two austral summers, with an ice-shelf-drilling campaign in 2019–2020 to access the ocean cavity28 and sediments below the TEIS to observe the changing system directly. We conducted detailed in situ hydrographic measurements in an area of the TEIS referred to as the ‘butterfly’12. The ice in this region is grounded at about 500 m below sea level (Figs. 1 and 2), typical of most of the Thwaites system outside the western trunk. We deployed the new underwater vehicle Icefin (Extended Data Fig. 1) through the borehole over five under-ice missions spanning 9–11 January 2020. The vehicle measured ocean temperature, salinity, dissolved oxygen and current velocities (Fig. 1 and Extended Data Fig. 2), mapped the sea floor and ice base in three dimensions (Figs. 1 and 2) and imaged the ice and sea floor (Fig. 3).
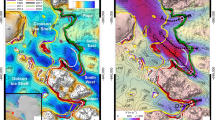
The sea-floor bathymetry near the TEIS GL is characterized by along-flow ridged bedforms having several different wavelengths, as well as evidence for two possible former GL positions (white and red boxes) and channelized subglacial outflow (black box). Data in a–d are from downward-facing bathymetric sonar and e from forward sonar on Icefin. Reworked sediments (white box) are observed near the borehole (yellow circle). b, A single sinuous 2–3-m-tall slope consistent with a GL sediment wedge is found about 200 m north of the 2016 GL estimated from remote sensing (red boxed region from a; red arrows denote wedge). The wedge crosscuts the 2–5-m wavelength along-flow bedforms (Extended Data Figs. 5 and 6). c, An isolated 4-m-deep channel cut into the sea floor makes two sharp turns and includes a segment that cuts perpendicular to most bedforms, suggesting that this feature formed from rerouting of subglacial water as the GL retreated (Extended Data Fig. 5). d, The bedform topography near the GL of T2 shows evidence of linear ridges striking north (Extended Data Fig. 4). e, Forward-looking sonar data of the ice base near the GL shows that the ice has the same 2–5-m-wavelength ridges as the shortest-wavelength features on the sea floor. These data together suggest that GL retreat has been largely continuous over the observable period, since at least 2011 based on remote sensing. Moreover, the similarities between the bed and ice morphology at the GL suggest that the ice–bed interactions set up slopes that are then progressively melted by the intruding seawater. Bathymetric sonar, a–d, was processed in Qimera and projected using QGIS. Forward sonar are projected using the Oculus ViewPoint software.
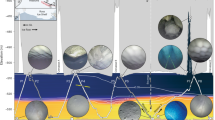
The Icefin vehicle track is shaded by relative along-track distance from downstream (white) to upstream (black). Light-blue data denote regions with cooling and freshening in terraces and dark blue denotes the coldest/freshest data observed. a, Conditions in the near-GL water cavity show the influence of melting (freshening) close to the GL along T2 (left). Coloured stars denote close passes to the ice that also have distinct signatures of mixing and melting. Vertical profiles of thermal driving (Θ − Θf), absolute salinity (SA) and dissolved oxygen (DO) binned with distance from the ice base show complex signatures that vary with location (Extended Data Fig. 3), suggesting the influence of both melting and SGW outflow (centre). Imagery near the GL (red box) shows ridged ice topography and sediment-laden clear basal ice at the GL (yellow star) (right). Scale bar, approximately 0.5 m. b, Ocean conditions in a large terrace formed in the ice base imply melting near the sidewalls (red boxes, 800 m from the GL along T2) (left). Warm, salty water (black, grey) is found along the sidewalls, whereas much fresher and more oxygenated water with low thermal driving (cold relative to in situ freezing) collects in the terrace roof (centre). Imagery of terrace sidewalls across the TEIS uniformly show scalloped surfaces reflecting turbulent melting (Extended Data Fig. 8 and Supplementary Video 1) (right). Scale bar, approximately 0.5 m. c, As in b but for a small terrace at 2,400 m downstream along T1 that contains cold, fresh and oxygen-rich water along its roof. Here the water becomes supercooled, with ice crystals forming laterally (right) across the heavily stratified interface (red box) between this 0.1 m upper boundary layer and the warm, saline and more oxygen-poor lower ocean waters. Scale bar, approximately 0.1 m.
Conditions under the ice shelf
The ice base deepened with distance from the GL, ranging from about 500 m to 520 m below sea level over the nearly 3 km T1 survey (Fig. 1b) and sloping downward more steeply along T2 from a minimum of 475 m depth at the GL (Fig. 1c). The sea floor (prograde) also sloped downward away from the GL (Figs. 1 and 2). The temperature, salinity and dissolved oxygen content of ocean water reflects mixing of different reservoirs, including ocean, melted glacial ice (glacial meltwater (GMW)) and subglacial water (SGW) from beneath the grounded ice. Warm water occupied much of the ocean under the TEIS, with maximum thermal driving of 2.25 °C (ocean temperatures 2.25 °C above the in situ freezing point), decreasing only slightly to 2 °C within about 5–10 m of the ice base and 400 m of the GL (Fig. 1b,c). This decrease in thermal driving resulted from pressure release, a cooling of the water from 0 °C to −0.25 °C and a freshening from 34.50 g kg−1 to 34.40 g kg−1 (Extended Data Fig. 2). Dissolved oxygen, which reflects both exchange with the atmosphere before submerging below the ice and that released from melting ice, increased in concentration over this region from 4.47 ml l−1 to 4.50 ml l−1; the coupled change in hydrographic conditions indicates a slight increase in GMW closer to the ice (Extended Data Fig. 3). The relatively well-mixed water column was overlain by a stratified upper layer, generally 5–10 m thick, at which the ocean cooled, freshened and increased in oxygen owing to local ice melt producing a greater admixture of GMW.
The sea floor was primarily characterized by bedform ridges oriented north–south parallel to glacier flow (Fig. 2). Sea-floor ridge–crest spacing varies by an order of magnitude from 3–25 m and tens of centimetres to 10 m heights; most ridges have 0.5–2 m heights (Extended Data Figs. 4–6). Sporadic boulders and drop stones are visible through the sediment (Fig. 3 and Supplementary Video 1). Near the borehole, troughs crosscutting the ridges suggest reworking of the sediment, which could occur if the glacier was pinned near this location that coincides with the estimated 2011 GL position12 (Fig. 2a). Upstream of the borehole, a single semi-linear feature cuts across the along-flow ridges and crests, with a sharp step in depth of 2–3 m height (Fig. 2b); this is downstream of all estimated GL positions for 2016–2017 (ref. 12). We interpret this feature as the sediment wedge produced when the ice shelf was grounded at this position, approximately 1,250 m from the end of the T1 survey and 1,500 m from the furthest upstream 2017 GL location. We observe no other clear evidence of GL wedges in this region. Thus, the bathymetry suggests that the GL retreated smoothly up the prograde sea floor, with only one stable location since at least 2011.
Local variations in ice-shelf basal slope (topography) influence melting through modulation of near-ice ocean-density gradients (stratification) and small-scale turbulence that control ocean heat and salt fluxes32,33,34,35,36,37,38. Nearest the GL, the ice base comprises a system of short-wavelength ridges (Fig. 2e) that have similar shape and 2–5-m spacing of small-amplitude (0.1–0.5 m) ridges in the sea floor (Fig. 2b–d and Extended Data Fig. 4) that overlay broad (about 50 m) topographic undulations. Within a kilometre of the GL, the ice surface is very rough, about 30% consisting of high slopes. Relatively clear ice laden with sediment, called basal ice, is found consistently in this region and in patches downstream, interrupting white, bubble-rich meteoric ice. The fine-grained (sand to mud) debris (Fig. 3a, right and Supplementary Video 1) and interspersed angular clasts ranging in size from a few to tens of centimetres comprises strong laminated layers in the basal ice at centimetre-scale spacing. Visible melting was observed throughout the region, with grains and small drop stones steadily falling out of basal ice, adding to the turbidity of the water column (Supplementary Video 1). Small terraces and scalloped morphology carved into the ice appear within 200 m of the GL, indicating that melting rapidly erodes these sloping ice faces. The steep faces grow in vertical scale with distance from the GL, showing progressive evolution of the shape of the ice from melting the longer it is exposed to the warm ocean.
The rough ice base observed at the GL erodes downstream, giving way to steep-sided, flat-roofed terraces (Figs. 1 and 3). The walls of these features form up to 90° angles to their flat roofs and keels, rising tens of centimetres to more than 6 m in height (Fig. 1b,c) and uniformly exhibiting scalloped surface textures (Fig. 3b, right), indicative of turbulent ocean-driven melting33. Terraces are also observed in crevasses. Conversely, the downstream ice under the TEIS is extremely flat, with surface slopes less than 5° (Figs. 1, 4 and 5). Ice-shelf basal topography carved by melt has been observed elsewhere, such as keels and channels29,39,40,41,42, including terraces at nearby Pine Island Glacier29 associated with steep slopes along marginal and channel features that were argued to form by means of feedback between slopes and melting. We observed terraces distributed across the TEIS, in many different orientations and across a range of horizontal and vertical scales, both associated with and independent of other basal features. Our observations argue that terraces are widespread basal features of ice shelves that overlay warm ocean cavities; these are not yet represented in most ice-shelf models.
Here the Icefin vehicle track is shaded by relative along-track distance from downstream (white) to upstream (black) and current velocities are shaded from slowest (white) to fastest (purple). a, Horizontal and vertical trends near a corner of a wide terrace (1,900 m downstream in T1 near the borehole) show freshening and cooling water inside the terrace and slowing currents as the water feels the influence of the ice interface. The grey lines denote the bottom of the terrace. Vertical profiles of ocean-current speed (U), thermal driving (Θ − Θf), absolute salinity (SA) and dissolved oxygen (DO) binned with distance from the ice base show that, although the water is warm close to the interface, the current velocity slows in the boundary layer, suggesting breaking from friction at the interface28. b,c, As in a for the furthest crevasse from the GL, observed along both T1 (b) and T2 (c). The panels on the right are binned with distance from the top of a step in the crevasse sidewall along T1 marked with the upper grey line. The lower grey line indicates the elevation of the bottom of the crevasse in T1. Stars in b relate to the location in the left panel. These panels show warm water with thermal driving of nearly 1.8 °C (Θ − Θf) reaching the crevasse walls accompanied by very slight freshening and oxygen increase that indicate melting (SA and DO) that would then rise into the crevasse.
a,b, Estimates of the spatially varying ice-shelf melt rate are shown for each of four subregions along T1 (a) and T2 (b) (r1–r4 are the same regions as in Extended Data Table 2). The ice surface is coloured by melt rate calculated along each slope (top panels) from the three-equation parameterization (Methods) under regionally averaged ocean conditions, demonstrating the increased melt rate along steep slopes. Horizontal coloured lines (bottom panels) correspond to the mean melt rates in each region. For regions r2 in T1 and r3 in T2, two means are presented, as conditions were observed to change with height in the crevasses, in which the water higher in the crevasses was colder and fresher than the water lower in these features. The lower bar indicates the melt rate determined by variable ocean forcing in the upper crevasse above the dashed lines in the top panels; the upper bar represents the mean melt rate below the dashed line in the crevasses. The means for each of these regions are as follows: T1: r1: 3.07 m year−1; r2: 16.16 m year−1 (below dashes), 9.72 m year−1 (above dashes); r3: 3.48 m year−1; r4: 4.11 m year−1; T2: r1: 1.47 m year−1; r2: 4.18 m year−1; r3: 9.12 m year−1 (below dashes), 6.82 m year−1 (above dashes); r4: 5.76 m year−1.
Ice–ocean interactions
In situ observations of the undisturbed ice–ocean boundary layer beneath ice shelves are inherently difficult to make through boreholes owing to contamination from the heated freshwater used to drill the access hole. Before this work, no in situ measurements existed that could constrain behaviour at the GL. To make these observations, we drove Icefin along the base of the ice to capture the boundary layer along flat interfaces, at an angle towards and then contacting the ice to measure gradients up to the ice, and straight into vertical sidewalls, in some cases measuring within about 5 cm of the interface.
Throughout the region, thermal driving was about 1.75 °C within 1 m of the ice base, providing ample heat to drive melting (Methods). Generally, the near-ice water column under the TEIS closely fits the well-defined mixing lines between GMW and a source water mass, and observations imply fully developed turbulent mixing35,37 (Methods and Extended Data Fig. 3), although data nearest the ice reflect increased melt. Our observations show strong vertical stratification approaching flat portions of the ice–ocean interface containing GMW formed from melting along neighbouring slopes rising to the ice base (Figs. 3 and 4). Ocean currents weaken within 5 m of the ice from a background speed near 3 cm s−1 (ref. 28) to near zero close to the interface (Fig. 4a). By contrast, currents increased in crevasses to a measured maximum of 5.90 cm s−1 (Fig. 4b,c).
In the terraces, dissolved oxygen increases with decreasing temperature and salinity, consistent with input from melting ice. Some of the strongest stratification we observed was in a shallow terrace formed along the roof of another large terrace, at which the salinity of the boundary layer was 20 g kg−1, or roughly one-third fresher than the surrounding ocean water. Extremely fresh layers (36–42% freshwater) in recesses along terrace roofs are not fully turbulent, as salinity and dissolved oxygen exhibit much larger signatures than temperature, suggesting a regime in which diffusive processes control heat and salt flux43. The thicknesses of these fresher layers are on the order of tens of centimetres and probably reflect the transition between the fully turbulent outer and viscous inner portions of the ice–ocean boundary layer44.
The water closest to the GL is cooler and fresher than the surrounding ocean (excluding freshwater in terrace roofs), with a dissolved oxygen signature distinct from elsewhere in the region. These data have a shallower temperature–salinity (T–S) slope of 2.05 °C (g kg−1)−1 than the melt mixing line (roughly 2.5 °C (g kg−1)−1) and decrease in dissolved oxygen with freshening (Extended Data Fig. 3). This admixture of fresh, oxygen-poor water suggests the presence of discharged SGW from upstream of the GL45. Although no SGW source is observed directly, bathymetry near the GL along T1 suggests a recent subglacial channel (Fig. 2c), and SGW outflow measured downstream varies over time28. Estimates of SGW concentration calculated from T–S and DO–S properties indicate maximum values of 7 ml l−1 and 24 ml l−1, respectively. The much higher SGW estimate implied from DO–S suggests that the debris-laden basal ice prevalent near the GL is also low in oxygen (such as ref. 45) and originated as SGW that was accreted in the overdeepened basin further upstream (Extended Data Fig. 7).
To test the impact of melting in the region, we calculated melt rates assuming shear-driven turbulent mixing, according to local-ice base slope and using current speeds and hydrographic conditions that were averaged over regions with similar conditions (denoted in Fig. 5). We compared these to results from three autonomous phase-sensitive radio echo sounders (ApRES) and the oceanographic mooring at the borehole28 (Fig. 5 and Methods). This approach using regionally averaged ocean conditions (Methods) yields average upward melt rates of 5 m year−1, but melt in the region is highly variable (Figs. 5 and 6). The stratification suppresses melting along flat interfaces, whereas estimated melt rates along vertical faces approach 30 m year−1.
a, Estimated spatially varying ice-shelf melt rates along T1 and T2 show the strong influence of local slope. Here each curve consists of individual melt-rate data points that have been calculated using the regionally averaged ocean conditions (Methods) corresponding to the regions labelled in Fig. 5. Red curves are from T1 and blue curves are from T2. b, Sideways melting along slopes greater than 30° contributes an estimated 27% of the melting under the TEIS, whereas these slopes account for only 9% of the ice base. Upward melting along low slopes is still the most notable source of melting, in which slopes less than 30° account for 73% of melting, while representing 91% of the ice.
Although stratification suppresses melting upward (moderate vertical melt or thinning), higher lateral turbulent mixing46 and destabilizing rising GMW36,47,48 allows warm water to reach sloped surfaces and promote melting (high sideways melt; Figs. 5 and 6). The scalloped ice surfaces observed only on steep faces is consistent with high sideways melting (Fig. 3b and Extended Data Fig. 8). Melting is strongest along the near-vertical walls of crevasses, at which water 1.8 °C above freezing was observed reaching within 1 m of the vertical crevasse wall (Fig. 4b). Water cools with height in the middle of the crevasses, freshens and becomes more oxygenated, suggesting a local accumulation of meltwater exceeding 3 ml l−1 from the erosion of the crevasse walls. Currents were faster in the crevasses by up to a factor of two compared with the background28, with flow speeds reaching about 6 cm s−1. These observations imply melt rates along the crevasse sidewalls of up to 43 m year−1 in one crevasse at the location of these observations (Methods), whereas melting elsewhere is more suppressed (Fig. 6; ref. 28).
Topographic controls on ice-shelf evolution
These results indicate that ice–ocean interactions under the TEIS are influenced by even small-scale ice topography, which would extend to other warm-based ice shelves in which low to moderate current speeds allow high levels of near-ice ocean stratification to persist. We calculate moderate average upward melting along flat surfaces at 5 m year−1, which matches measured melt rates on similar interfaces from three long-term ApRES and mooring data28 and are consistent with the historical estimates from ice-penetrating radar18. Nearest to the GL along each survey line, melt rates average 2 m year−1 but range from 1 to 10 m year−1 (Figs. 5 and 6). Our observations show that the feedback between ice slope and melting is relevant to the entire base of ice shelves, including near the GL. The varied topography of the ice base at the GL, carved as it flowed over the bed before reaching the ocean, becomes a broadly distributed network of sloped ice surfaces along which melting is promoted.
Our observations suggest that melting along sloped ice is an important factor in the total ice loss near the GL of Thwaites Glacier. In the region surveyed, 27% of the total melting occurs along slopes that are greater than 30° (Fig. 6). Because crevasses funnel water through them28 at rates that can efficiently transfer heat and salt into the steep crevasse walls (Fig. 4), these locally high melt rates should widen both crevasses and basal rifts across the glacier, including the TGT and the TEIS, and could contribute to increased calving of the glacier8,10. The rough topography near the GL may enable melting to persist in this region despite low current speeds. Our work implies that basal melting of warm-based ice shelves is heterogeneous and exploits ice topography inherited from interactions with the bed and formed by crevassing. Such effects are challenging to observe, not yet captured in models of GL retreat and probably contribute to the loss of ice elsewhere along the Antarctic coast.
Methods
Icefin vehicle
The Icefin vehicle49 is a modular, hybrid, remotely operated vehicle with autonomous capabilities that was designed for use through holes bored or melted in ice (Extended Data Fig. 1). For this work, Icefin was fitted with sensors for scientific analysis of the ice–ocean system and navigation (Extended Data Table 1). Most water-column sensors are located in the vehicle nose to provide undisturbed water flow. Forward cameras, lights and sonar provide perception for science and navigation, and bathymetric sonar maps sea-floor geometry. A high-definition camera and Doppler velocity logger (DVL) with acoustic Doppler current profiler (ADCP) point in the same sense, and altimeter in the opposite sense, in the navigation module that can be oriented down (sea-floor facing) or up (ice facing). A rear-facing camera monitors the tether/tail. Guidance, navigation and control of Icefin allow for geolocated scientific data through the fusion of an advanced fibre-optic gyroscope inertial measurement unit, compass, DVL, altimeter and pressure sensor providing low-level motion control and high-level localization. The five thrusters provide five degrees of freedom movement, control pitch, yaw, heave and sway without protruding surfaces, and permit hovering. Icefin is rated to 1.5 km depth, weighs 120 kg in air, is 23 cm wide and 4.5 m long. At the TEIS, Icefin was deployed vertically from an articulating launch and recovery system, lowered through the borehole by means of a 3.5-km-long 4-mm-diameter Kevlar-reinforced (1,800 lb breaking strength; Linden) fibre optic attached to a strength-enforced termination at the vehicle, enabling control, communication and data retrieval.
Icefin was deployed for five 6–8-h missions during 11–14 January 2020 to map environmental gradients in cross-section extending seaward from the GL, overlapping surface, airborne and ApRES surveys. The Icefin data are grouped into two composite profiles, transect 1 (T1) and transect 2 (T2); T1 consists of missions 1 (about 1.2 km south), 2 (about 1.9 km south) and 3 (about 1 km north) and T2 is mission 4 (about 1.6 km southeast). Missions 1-4 were conducted with the navigation module down and mission 5 with the navigation module up. Multipath in the clear basal ice reduced vehicle positioning accuracy in mission 5. T2 intersected the GL at 104.780° W, 75.214° S. For missions 1 and 3, the vehicle conducted survey segments alternating between pitching up towards the ice and down towards the sea floor at about 20–30° to acquire hydrographic profiles while making forward progress, similar to ocean gliders.
Post-processing of hydrographic data
Hydrographic data come from three sensors on Icefin: conductivity–temperature (C–T), pressure (P) and DO sensors. All sensors were factory calibrated before the fieldwork. C–T and DO sensors were field calibrated. Pressure measurements (1 Hz) were interpolated to match the 5-Hz C–T data to derive hydrographic variables. DO measurements (1 Hz) were not interpolated.
Data post-processing
-
1.
Remove background atmospheric pressure,
-
2.
Remove outliers ±2 standard deviations from mean for C–T and DO (excluding borehole data),
-
3.
Apply three-point weighted mean filter to C–T, P and DO,
-
4.
Align C and T measurements with time lag (0 s lag produced the best results),
-
5.
Remove C, T and DO data for vehicle speeds <5 cm s−1,
-
6.
Derive hydrographic variables (conservative temperature, absolute salinity, density and so on) using TEOS-10 (ref. 50),
-
7.
Remove pressure/salinity effects on DO51.
Post-processing ocean-current speeds
Ocean-current speeds are derived from the onboard DVL/ADCP, which calculates the X, Y and Z vehicle velocities (major, minor and vertical axes) and retrieves water-column velocities in 2-m bins at a variable start distance from the vehicle. The minimum altitude from an interface for current profiling to occur is 10 m; gradients in vehicle pitch, roll, heading and speed dictate the distance of the first bin from the vehicle and sampling frequency (maximum 5 Hz). We subsample velocities to 1 Hz. Water-column X velocities are differenced from the vehicle velocity, resulting in an uncertainty of ≤1 cm s−1. Vehicle Y and Z velocities are substantially lower than X, so Y and Z velocity uncertainties are likewise lower. Here we only analyse X and Y velocities.
Data post-processing:
-
1.
Remove data in out-of-range bins (for example, below sea floor, above ice base),
-
2.
Remove spurious data: exactly 0 m s−1 or 32,767 m s−1,
-
3.
Remove measurements when vehicle pitch or roll >+/−30°,
-
4.
Convert from vehicle reference frame to geographic reference frame,
-
5.
Apply 30 s mean filter,
-
6.
Filter for gradients <1 standard deviation from mean vehicle speed, pitch, roll and individual bin velocity,
-
7.
Collate bins by each up/down vehicle swoop into 1-m vertical bins, removing data >1 standard deviation of the mean for that range.
Post-processing of ice and sea-floor elevations
Ice-base and sea-floor elevations are derived from DVL and altimeter data and bathymetric sonar data. The DVL takes into account pitch, roll and heading when producing ranges and the altimeter and sonar data are corrected for these attitudes. Bathymetric sonar was processed in Qimera, in which obvious outliers were filtered or cleaned by hand.
Data post-processing (DVL, altimeter):
-
1.
Remove data >2 standard deviations of the mean gradient in interface elevation (ice base or sea floor),
-
2.
Manually remove outliers.
After post-processing, 94% of ice-base measurements had horizontal resolution 26 ± 14 cm, with minimum and maximum spacings of 1.4 mm and 3.38 m, respectively. Ninety-three percent of sea-floor data had horizontal resolution 29 ± 20 cm and minimum and maximum spacings of 2.3 mm and 4.72 m, respectively.
Water-mass partition
We use a three-point endmember partition35 to estimate concentrations of water masses below the shelf, which assumes that hydrographic properties (Θ, SA and DO) reflect a mixture of three water masses:
-
1.
A source water mass (SRC) responsible for driving melt: Θ = −0.21 °C, SA = 34.50 g kg−1, DO = 4.48 ml l−1,
-
2.
GMW from local ice-shelf melt: Θ = −92.50 °C, SA = 0 g kg−1, DO = 25.20 ml l−1,
-
3.
SGW discharged from upstream beneath the grounded glacier52: Θ = −0.34 °C, SA = 0 g kg−1, DO = 1.61 ml l−1.
This partition uses conservative tracers that only vary as a result of a physical mixture of water masses and mix under fully turbulent conditions35,37. Subsets of the data not in a fully turbulent mixing regime are excluded from the partition. These data are easily identified by double-diffusive characteristics—large changes in SA (and DO) relative to Θ that result from faster molecular diffusion of heat than salt43,44.
The source water mass (SRC, red star in Extended Data Fig. 3 and Fig. 4b) is the warmest, saltiest and most oxygen-depleted point in the T–S and DO–S space that fits the GMW mixing line on which our data lie: T–S and DO–S slopes of −2.49 °C (g kg−1)−1 and 0.60 ml l−1 (g kg−1)−1, respectively. SRC generally resides 10 m below the ice base (outside crevasses). Warmer, saltier and more oxygen-depleted data (red data in Extended Data Fig. 3) further down in the water column exhibit a different slope in the T–S (−2.74 °C (g kg−1)−1) and DO–S (0.35 ml l−1 (g kg−1)−1) space, suggestive of mixing processes not derived from local glacial modification. Thus, SRC hydrographic properties represent the local water mass melting the ice shelf, referred to as a composite tracer35. SRC is a derivative mixture of modified CDW and winter water that resides around the depth of the highly variable pycnocline separating these water masses in Pine Island Bay. Relatively weak inflow of about 3 cm s−1 into our study region and at a distance of about 75 km from Pine Island Bay28 results in a ventilation period of around one month for SRC. During this time Θ, SA and DO properties could be altered through interaction with the ice base along other sections of the TEIS, consumption by organisms or mixture with other water masses. We forgo choosing hydrographic properties for the absolute source water mass to ensure that the properties used in our three-point water-mass partition are conservative for local ice–ocean interactions.
The Θ and SA values for GMW consider the latent heat loss associated with phase change from solid to liquid freshwater. An extrapolation of the Gade or GMW mixing line35,37 for our data to 0 g kg−1 results in an effective temperature of −86.46 °C. GMW is high in DO because of air bubbles in meteoric ice that dissolve into solution when melted. An extrapolation of the DO–S mixing line to 0 g kg−1 for our data results in a DO concentration of 25.20 ml l−1.
The Θ and SA values for SGW represent freshwater at the pressure-depressed freezing point at GL depth of 480 m in T2 (Fig. 1c). We use in situ DO measurements from Lake Whillans, West Antarctica45 for the SGW endmember, as active subglacial lakes exist upstream of the TEIS53,54,55. Thus, we expect that basal ice here should carry similarly low DO.
Three-equation melt parameterization
We estimate ice-shelf melt rates along T1 and T2 using the three-equation boundary layer (BL) parameterization for heat and salt transfer between the ocean and ice56, which assumes that shear-driven turbulence controls ice melt as the dominant mechanism conveying heat and salt to the viscous sublayer (VSL), beyond which molecular diffusion operates57. Near-ice ocean-current measurements exhibit shear (Fig. 4a), which agrees with the physics governing Ekman layers28 and is consistent with shear-driven turbulence.
This assumption does not hold for regions with low current speeds, at which molecular processes and diffusive convection dictate heat and salt fluxes at distances greater than the typical VSL44,58, order several millimetres56. We only observed such conditions in two small regions along the roofs of two terraces with extremely fresh layers (S ≈ 20 psu) tens of centimetres thick (Fig. 3b,c) that did not hold fully turbulent mixing lines and exhibited larger salinity gradients than temperature. Other near-ice ocean data did not exhibit these thick, fresh layers but instead gradually cooled and freshened towards the ice throughout the surveyed area. This density change stabilizes the BL beneath regions of the ice base, reducing vertical shear-driven turbulent mixing59. Therefore, although shear-driven turbulence dominates heat and salt fluxes, turbulent fluxes are modified by stratification47,60. We account for stratification in our melt rates.
The three-equation BL parameterization is as follows:
Equation (1) represents temperature, practical salinity and pressure at the ice–ocean interface, in which a = −5.73 × 10−2 °C (g kg−1)−1, b = 9.39 × 10−2 and c = −7.53 × 10−8 °C Pa−1 are constants and TB is always at the freezing point. TB and SB are not directly observed and are estimated below.
Equation (2) represents the heat flux balance and equation (3) represents the salt flux balance, in which \({Q}_{{\rm{O}}}^{{\rm{S}}}\) is the ocean salt flux towards the ice, \({Q}_{{\rm{I}}}^{{\rm{S}}}\) is the diffusive salt flux through the ice (0 here) and \({Q}_{{\rm{Fresh}}}^{{\rm{S}}}\) is the freshwater flux from melting. \({Q}_{{\rm{O}}}^{{\rm{T}}}\) is the ocean sensible heat flux into the ice base, \({Q}_{{\rm{I}}}^{{\rm{T}}}\) is the conductive heat flux through the ice shelf and \({Q}_{{\rm{Latent}}}^{{\rm{T}}}\) is the latent heat removed during melting:
In equation (4), ρw and T represent the density and temperature, respectively, of seawater outside the BL/VSL. For seawater, cp = 3,974 J kg−1 °C−1, the friction velocity u* is the kinematic stress at the ice–ocean interface and the heat transfer coefficient ΓT describes turbulent mixing of heat across the BL. The density of ice is ρi = 918 kg m−3, LF = 3.34 × 105 J kg−1 is latent heat of fusion and \(\dot{m}\) is the ice-shelf melt rate (m year−1), in which \(\dot{m}\) is positive for melting. We use the quadratic stress formula to relate u* to near-ice current speeds61:
in which CD = 2.2 × 10−3 is a dimensionless drag coefficient assumed to be constant27 and U is the current speed. Without a vertical-ice-column temperature profile, we vary \({Q}_{{\rm{I}}}^{{\rm{T}}}\) as 0.12–0.2 of the magnitude of \({Q}_{{\rm{O}}}^{{\rm{T}}}\) (refs. 42,62).
Equations (7) and (8) resemble equations (4) and (5), in which S is salinity outside the BL/VSL, SB is the ice–ocean interface salinity and SI is the salinity of the ice shelf (considered 0 here). The salt transfer coefficient ΓS is much smaller than ΓT, owing to slower molecular diffusion of salt than heat in the VSL63. We consider a range of published values for ΓS between \(\frac{1}{70}\) and \(\frac{1}{25}\) of ΓT (refs. 23,57,59) and choose the ratio that produces optimal agreement between melt rates derived by the heat flux and salt flux equations.
We estimated melt rates in five subregions based on ice-base characteristics and near-ice ocean conditions T, S and U (Fig. 5). We compiled integrated probability density functions of the ocean conditions in each subregion, then consider the 25th, 50th and 75th percentiles of T and S within 5 m of the ice base and the 50th, 75th and 100th percentiles of U within 10 m of the ice base for each subregion. We select higher percentiles (and therefore speeds) for U because observed ocean currents increased towards the ice (ref. 28; Fig. 4) before slowing from friction (ref. 28; Fig. 4) and because less current data were collected near the ice base. Extended Data Table 2 provides ocean properties entered into equations (4), (7) and (8). We then consider an array of ten values for the ice–ocean interface properties (TB, SB) by varying SB from the minimum observed salinity to the 75th percentile of S for each subregion and then converted to TB using equation (1) for the ice-base mean pressure.
We estimate ΓT by dividing the published range of the thermal Stanton number (\({{C}_{{\rm{D}}}^{1/2}\varGamma }_{{\rm{T}}}\) = 2.18 × 10−4 – 1.10 × 10−3) from observations beneath ice shelves24,55 by CD, yielding ΓT = 4.60 × 10−3–2.35 × 10−2, then considering that ΓS ranges between \(\frac{1}{70}\) and \(\frac{1}{25}\) of ΓT. We vary ΓT and ΓS from their minimum to maximum values based on the sine of the ice-base slope, from 0° to 90°, because slope/roughness of the ice interacts with stratification to produce variable melting36,48,63,64,65, and rising buoyant GMW also destabilizes stratification along steep ice slopes. The equations by which we calculated this are as follows:
We compared calculated melt rates to ApRES data at three locations38: T1 distance 2,250–2,857 m; region 2: T1 distance 1,810–1,904 m and T2 distance 1,480–1,608 m; and region 3: T1 distance 0–960 m. The set of conditions that produced the best fit to the observed melt rates along the flat (slope <5°) ice base were the 75th percentile of T and S, the 100th percentile of U and nearly the freshest SB and warmest TB, with heat conduction \({Q}_{{\rm{I}}}^{{\rm{T}}}=0.12{Q}_{{\rm{I}}}^{{\rm{T}}}\) and salt transfer coefficient ΓS = \(\frac{1}{45}\)ΓT = 1.03 × 10−4–5.21 × 10−4. The best-fit melt-rate estimates are: region 1: 3.41 m year−1 versus 3 m year−1 observed; region 2: 4.80 m year−1 (T1) and 4.65 m year−1 (T2) versus 5 m year−1 observed; region 3: 2.37 m year−1 versus 2 m year−1 observed.
We compared stratified, shear-driven turbulent estimates to those for an assumed diffusive-convective melt rate47, considering \({Q}_{{\rm{I}}}^{{\rm{T}}}=0.12{Q}_{{\rm{O}}}^{{\rm{T}}}\):
in which kT = 1.40 × 10−7 m2 s−1 is the molecular diffusion (conduction) of heat, ks = 1.30 × 10−9 m2 s−1 is the molecular diffusion of salt and t is the amount of time that diffusive convection has driven melting. For t = 1 h, the diffusive-convective melt rate gives 2.26 m year−1 for region 1, 2.35 m year−1 for region 2 and 2.06 m year−1 for region 3. At t = 1 day, the melt rate decreases to 0.46 m year−1 for region 1, 0.48 m year−1 for region 2 and 0.42 m year−1 for region 3. At t = 1 week, the melt estimate decreases to 0.17 m year−1 for region 1, 0.18 m year−1 for region 2 and 0.16 m year−1 for region 3. Although diffusive convection melt rates initially resemble those observed, they abate to <10% of the observations within a week as the BL grows. The ApRES melt rate time series do not exhibit this decrease, showing that, although stratification inhibits turbulence, current shear still determines the melt rate along flat and low-sloped regions of the survey area.
Tuning the melt rate uniformly over the survey region overestimates melt along portions of the ice base that are in diffusive regimes and possibly in the unmapped tops of crevasses; however, this is a small fraction of the region surveyed. Ocean properties will cool/freshen with height in the crevasses and current speeds may change compared with the lower 10% surveyed (ref. 28; Fig. 4). This approach however underestimates melt rates along steep ice slopes below the upper crevasse sections, because low SB (22.14 psu) and therefore high TB reduces assumed thermal forcing (T − TB): the ApRES at the borehole measured lateral melt rates of 70 m year−1 on the terrace wall (mean slope 79°) at 1,800 m along T1, compared with 26.35 m year−1 estimated. Changing to a salinity of 34.28 psu (75th percentile for T1 subregion 3) obtains a melt rate of 45.97 m year−1, closer to observed.
We also compared shear-driven melt rates to those from a buoyancy-driven turbulent melt-rate parameterization36:
in which φ is the ice slope and T − Tf is thermal driving outside the BL/VSL. For slope φ = 79°, S = 34.28 psu and T = −0.34 °C (75th percentile for T1 subregion 3), the buoyancy-driven melt-rate estimate is 18.43 m year−1, considerably lower than that observed and 45.97 m year−1 estimated from shear-driven turbulence, and does not account for \({Q}_{{\rm{I}}}^{{\rm{T}}}=0.12{Q}_{{\rm{O}}}^{{\rm{T}}}\). Ocean conditions at the opposing crevasse wall are warmer (−0.33 to −0.28 °C) and saltier (34.26–34.27 psu) than what we use to estimate melt on the terrace wall, suggesting that conditions are warmer near the ice or vertical velocities increase turbulence, increasing melt.
Statistics
All statistics were performed in MATLAB. The above sections provide the details of these statistical analyses, with the underlying mean and standard deviation functions being native to MATLAB.
Data availability
The datasets generated and/or analysed during the present study have been submitted to https://www.usap-dc.org/ and are available at https://doi.org/10.15784/601618. The processing and figure-plotting scripts are available at https://doi.org/10.5281/zenodo.7278005.
Change history
24 February 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41586-023-05861-8
References
Rignot, E. et al. Recent Antarctic ice mass loss from radar interferometry and regional climate modelling. Nat. Geosci. 1, 106–110 (2008).
Mouginot, J., Rignot, E. & Scheuchl, B. Sustained increase in ice discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013. Geophys. Res. Lett. 41, 1576–1584 (2014).
Rignot, E. et al. Four decades of Antarctic Ice Sheet mass balance from 1979–2017. Proc. Natl Acad. Sci. 116, 1095–1103 (2019).
Scambos, T. A. et al. How much, how fast?: A science review and outlook for research on the instability of Antarctica’s Thwaites Glacier in the 21st century. Global Planet. Change 153, 16–34 (2017).
Morlighem, M. et al. Deep glacial troughs and stabilizing ridges unveiled beneath the margins of the Antarctic ice sheet. Nat. Geosci. 13, 132–137 (2020).
Joughin, I., Smith, B. E. & Medley, B. Marine ice sheet collapse potentially under way for the Thwaites Glacier Basin, West Antarctica. Science 344, 735–738 (2014).
Schoof, C. Ice sheet grounding line dynamics: steady states, stability, and hysteresis. J. Geophys. Res. Earth Surf. 112, F03S28 (2007).
Miles, B. W. J. et al. Intermittent structural weakening and acceleration of the Thwaites Glacier Tongue between 2000 and 2018. J. Glaciol. 66, 485–495 (2020).
Bevan, S. L., Luckman, A. J., Benn, D. I., Adusumilli, S. & Crawford, A. Brief communication: Thwaites Glacier cavity evolution. Cryosphere 15, 3317–3328 (2021).
Alley, K. E. et al. Two decades of dynamic change and progressive destabilization on the Thwaites Eastern Ice Shelf. Cryosphere 15, 5187–5203 (2021).
Rignot, E., Mouginot, J., Morlighem, M., Seroussi, H. & Scheuchl, B. Widespread, rapid grounding line retreat of Pine Island, Thwaites, Smith, and Kohler glaciers, West Antarctica, from 1992 to 2011. Geophys. Res. Lett. 41, 3502–3509 (2014).
Milillo, P. et al. Heterogeneous retreat and ice melt of Thwaites Glacier, West Antarctica. Sci. Adv. 5, eaau3433 (2019).
Thoma, M., Jenkins, A., Holland, D. & Jacobs, S. Modelling circumpolar deep water intrusions on the Amundsen Sea continental shelf, Antarctica. Geophys. Res. Lett. 35, L18602 (2008).
Jacobs, S. S., Hellmer, H. H. & Jenkins, A. Antarctic ice sheet melting in the Southeast Pacific. Geophys. Res. Lett. 23, 957–960 (1996).
Jacobs, S. S., Jenkins, A., Giulivi, C. F. & Dutrieux, P. Stronger ocean circulation and increased melting under Pine Island Glacier ice shelf. Nat. Geosci. 4, 519–523 (2011).
Webber, B. G. et al. Mechanisms driving variability in the ocean forcing of Pine Island Glacier. Nat. Commun. 8, 14507 (2017).
Wåhlin, A. K. et al. Pathways and modification of warm water flowing beneath Thwaites Ice Shelf, West Antarctica. Sci. Adv. 7, eabd7254 (2021).
Schroeder, D. M. et al. Multidecadal observations of the Antarctic ice sheet from restored analog radar records. Proc. Natl Acad. Sci. 116, 18867–18873 (2019).
Rignot, E., Jacobs, S., Mouginot, J. & Scheuchl, B. Ice-shelf melting around Antarctica. Science 341, 266–270 (2013).
Pritchard, H. et al. Antarctic ice-sheet loss driven by basal melting of ice shelves. Nature 484, 502–505 (2012).
Nicholls, K. W. et al. Measurements beneath an Antarctic ice shelf using an autonomous underwater vehicle. Geophys. Res. Lett. 33, L08612 (2006).
Jenkins, A., Nicholls, K. W. & Corr, H. F. Observation and parameterization of ablation at the base of Ronne Ice Shelf, Antarctica. J. Phys. Oceanogr. 40, 2298–2312 (2010).
Jenkins, A. et al. Observations beneath Pine Island Glacier in West Antarctica and implications for its retreat. Nat. Geosci. 3, 468–472 (2010).
Stanton, T. P. et al. Channelized ice melting in the ocean boundary layer beneath Pine Island Glacier, Antarctica. Science 341, 1236–1239 (2013).
Begeman, C. B. et al. Ocean stratification and low melt rates at the Ross Ice Shelf grounding zone. J. Geophys. Res. Oceans 123, 7438–7452 (2018).
Stewart, C. L. et al. Basal melting of Ross Ice Shelf from solar heat absorption in an ice-front polynya. Nat. Geosci. 12, 435–440 (2019).
Davis, P. E. & Nicholls, K. W. Turbulence observations beneath Larsen C ice shelf, Antarctica. J. Geophys. Res. Oceans 124, 5529–5550 (2019).
Davis, P. E. D. et al. Suppressed basal melting in the eastern Thwaites Glacier grounding zone. Nature 614, 479–485 (2023).
Dutrieux, P. et al. Basal terraces on melting ice shelves. Geophys. Res. Lett. 41, 5506–5513 (2014).
Washam, P., Nicholls, K. W., Münchow, A. & Padman, L. Summer surface melt thins Petermann Gletscher Ice Shelf by enhancing channelized basal melt. J. Glaciol. 65, 662–674 (2019).
Seroussi, H. et al. Continued retreat of Thwaites Glacier, West Antarctica, controlled by bed topography and ocean circulation. Geophys. Res. Lett. 44, 6191–6199 (2017).
Bushuk, M., Holland, D. M., Stanton, T. P., Stern, A. & Gray, C. Ice scallops: a laboratory investigation of the ice–water interface. J. Fluid Mech. 873, 942–976 (2019).
Couston, L. A. et al. Topography generation by melting and freezing in a turbulent shear flow. J. Fluid Mech. 911, A44 (2021).
Gwyther, D. E., Galton-Fenzi, B. K., Dinniman, M. S., Roberts, J. L. & Hunter, J. R. The effect of basal friction on melting and freezing in ice shelf–ocean models. Ocean Model. 95, 38–52 (2015).
Jenkins, A. The impact of melting ice on ocean waters. J. Phys. Oceanogr. 29, 2370–2381 (1999).
McConnochie, C. D. & Kerr, R. C. Dissolution of a sloping solid surface by turbulent compositional convection. J. Fluid Mech. 846, 563–577 (2018).
Gade, H. G. Melting of ice in sea water: a primitive model with application to the Antarctic ice shelf and icebergs. J. Phys. Oceanogr. 9, 189–198 (1979).
Malyarenko, A. et al. A synthesis of thermodynamic ablation at ice–ocean interfaces from theory, observations and models. Ocean Model. 154, 101692 (2020).
Rignot, E. & Steffen, K. Channelized bottom melting and stability of floating ice shelves. Geophys. Res. Lett. 35, L02503 (2008).
Alley, K. E., Scambos, T. A., Siegfried, M. R. & Fricker, H. A. Impacts of warm water on Antarctic ice shelf stability through basal channel formation. Nat. Geosci. 9, 290–293 (2016).
Marsh, O. J. et al. High basal melting forming a channel at the grounding line of Ross Ice Shelf, Antarctica. Geophys. Res. Lett. 43, 250–255 (2016).
Washam, P., Nicholls, K. W., Münchow, A. & Padman, L. Tidal modulation of buoyant flow and basal melt beneath Petermann Gletscher Ice Shelf, Greenland. J. Geophys. Res. Oceans 125, e2020JC016427 (2020).
Kimura, S., Nicholls, K. W. & Venables, E. Estimation of ice shelf melt rate in the presence of a thermohaline staircase. J. Phys. Oceanogr. 45, 133–148 (2015).
McPhee, M. G., Maykut, G. A. & Morison, J. H. Dynamics and thermodynamics of the ice/upper ocean system in the marginal ice zone of the Greenland Sea. J. Geophys. Res. Oceans 92, 7017–7031 (1987).
Christner, B. C. et al. A microbial ecosystem beneath the West Antarctic ice sheet. Nature 512, 310–313 (2014).
Gregg, M. C. Diapycnal mixing in the thermocline: a review. J. Geophys. Res. Oceans 92, 5249–5286 (1987).
Rosevear, M. G., Gayen, B. & Galton-Fenzi, B. K. Regimes and transitions in the basal melting of Antarctic ice shelves. J. Phys. Oceanogr. 52, 2589–2608 (2022).
Kerr, R. C. & McConnochie, C. D. Dissolution of a vertical solid surface by turbulent compositional convection. J. Fluid Mech. 765, 211–228 (2015).
Meister, M. R., et al. Icefin: redesign and 2017 Antarctic field deployment. https://doi.org/10.1109/OCEANS.2018.8604725 (2019).
McDougall, T. J. & Barker, P. M. Getting started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox. SCOR/IAPSO WG 127, 28 pp (2011).
Uchida, H., Johnson, G. C., & McTaggart, K. E. CTD oxygen sensor calibration procedures. https://doi.org/10.25607/OBP-1344 (2010).
Joughin, I. R., Tulaczyk, S. & Engelhardt, H. F. Basal melt beneath Whillans ice stream and ice streams A and C, West Antarctica. Ann. Glaciol. 36, 257–262 (2003).
Smith, B. E., Gourmelen, N., Huth, A. & Joughin, I. Connected subglacial lake drainage beneath Thwaites Glacier, West Antarctica. Cryosphere 11, 451–467 (2017).
Malczyk, G., Gourmelen, N., Goldberg, D., Wuite, J. & Nagler, T. Repeat subglacial lake drainage and filling beneath Thwaites Glacier. Geophys. Res. Lett. 47, e2020GL089658 (2020).
Hoffman, A. O., Christianson, K., Shapero, D., Smith, B. E. & Joughin, I. Brief communication: Heterogenous thinning and subglacial lake activity on Thwaites Glacier, West Antarctica. Cryosphere 14, 4603–4609 (2020).
Holland, D. M. & Jenkins, A. Modeling thermodynamic ice–ocean interactions at the base of an ice shelf. J. Phys. Oceanogr. 29, 1787–1800 (1999).
Jenkins, A. A one‐dimensional model of ice shelf‐ocean interaction. J. Geophys. Res. Oceans 96, 20671–20677 (1991).
Rosevear, M. G., Gayen, B. & Galton-Fenzi, B. K. The role of double-diffusive convection in basal melting of Antarctic ice shelves. Proc. Natl Acad. Sci. 118, e2007541118 (2021).
McPhee, M. G., Morison, J. H. & Nilsen, F. Revisiting heat and salt exchange at the ice‐ocean interface: ocean flux and modeling considerations. J. Geophys. Res. Oceans 113, C06014 (2008).
Vreugdenhil, C. A. & Taylor, J. R. Stratification effects in the turbulent boundary layer beneath a melting ice shelf: insights from resolved large-eddy simulations. J. Phys. Oceanogr. 49, 1905–1925 (2019).
McPhee, M. G. The effect of the oceanic boundary layer on the mean drift of pack ice: application of a simple model. J. Phys. Oceanogr. 9, 388–400 (1979).
Arzeno, I. B. et al. Ocean variability contributing to basal melt rate near the ice front of Ross Ice Shelf, Antarctica. J. Geophys. Res. Oceans 119, 4214–4233 (2014).
Steele, M., Mellor, G. L. & Mcphee, M. G. Role of the molecular sublayer in the melting or freezing of sea ice. J. Phys. Oceanogr. 19, 139–147 (1989).
Morlighem, M. et al. BedMachine v3: complete bed topography and ocean bathymetry mapping of Greenland from multibeam echo sounding combined with mass conservation. Geophys. Res. Lett. 44, 11,051–11,061 (2017).
Mondal, M., Gayen, B., Griffiths, R. W., & Kerr, R. C. Ablation of sloping ice faces into polar seawater. J. Fluid Mech. 863, 545–571 (2019).
Gardner, A. S., Fahnestock, M. A. & Scambos, T. A. MEaSUREs ITS_LIVE regional glacier and ice sheet surface velocities, version 1. Data archived at NASA National Snow and Ice Data Center Distributed Active Archive Center. https://doi.org/10.5067/6II6VW8LLWJ7 (2021).
Acknowledgements
We thank the personnel from the United States Antarctic Program and the British Antarctic Survey, without whom these data could not be collected. Fieldwork and support for analysis was provided by the NSF-NERC International Thwaites Glacier Collaboration (ITGC), financed by NSF OPP grant 1739003 (US), NERC NE/S006656/1, NERC NE/S006761/1 and NERC NE/S006427/1 (UK). We recognize the support of the ITGC staff and scientists in the execution of this ambitious field campaign. The Icefin team acknowledges past Georgia Tech team members who helped develop and field the vehicle: J. Lutz, M. ‘Kit’ Philleo, C. Ramey, C. Walker, J. Buffo, T. Hobbs and School of Earth and Atmospheric Sciences (EAS) chair G. Huey and the EAS staff who supported this work. The Icefin vehicle was initially developed with funding from Georgia Institute of Technology and startup funds for B.E.S. Now in its third version, Icefin was redesigned under NASA grant NNX16AL07G, principal investigator B.E.S. The Icefin project is now located at Cornell University.
Author information
Authors and Affiliations
Contributions
B.E.S. led the Icefin vehicle development and field team, drove the vehicle, drafted the paper and processed imaging and sonar data. P.W. participated in early-season fieldwork near McMurdo Station, analysed hydrographic data, produced figures and helped write the paper. P.E.D.D., K.W.N., D.M.H., K.L.R. and J.A.S. participated in the ITGC field campaign, helped formulate ideas and discussed analyses, J.D.L. and A.S. helped develop Icefin and the data analysis pipeline, participated in the early season field work, and discussion, E.C. participated in the field campaign and data discussion, D.J.G.D. and A.D.M. helped develop Icefin, operated the vehicle and participated in the ITGC field campaign, B.Y. participated in data discussions, P.A. developed the hot water drill and drilled the access hole, M.R.M., was lead engineer for Icefin and B.C.H., E.S.Q. and F.E.B. helped develop and field Icefin, C.T., J.W., A.B.-F. and D.G.V. participated in the field campaign and S.A., E.R., J.P. and K.M. helped obtain funding for the project and discussed the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Susheel Adusumilli, Craig Lee, Craig McConnochie and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 The Icefin vehicle is a modular underwater vehicle designed to deploy through boreholes in the ice (diagram produced using SolidWorks).
The vehicle consists of a total of seven modules: forward science including oceanographic sensors (CTD, DO), forward-looking sonar, cameras and lighting; forward directional thrusters; customizable science payload, shown here as configured for the Thwaites missions with a bathymetric sonar; electronics module; aft science and navigation module with DVL/ADCP, altimeter, high-definition camera and light; aft directional thruster; and rear thruster with rear camera. The fibre-optic tether mounts to a bridle at the tail of the vehicle and connects through the rear bulkhead of the electronics module, delivering live data feeds to the surface.
Extended Data Fig. 2 Salinity and dissolved oxygen generally track with temperature near the retreating GL of the TEIS.
a, As in Fig. 1, image of the TEIS, with historical GL positions in coloured lines showing notable retreat over the past two decades (QGIS map: Landsat 8, 15 m pixel−1, band 8 image LC08_L1GT_003113_20200131_20200211_01_T2_B8, 31 January 2020; the red box denotes the study region); inset denotes the geographic location of the TEIS in relation to Antarctica. b–g, Hydrography of the ocean under the ice shows that absolute salinity (d,e) and dissolved oxygen (f,g) track with temperature (Fig. 1b,c) under the TEIS. The inset in b provides a focused view of the study region: the yellow circle denotes the location of the hot-water-drilled access hole, the red line represents T1 (5–10° oblique to the flow direction of the glacier) and the blue line represents T2 (50° oblique to flow). Triangles in b–g mark historic GL locations estimated from satellite data12 (white, 2011; blue, 2016–2017) and shown by the Icefin bathymetric sonar data (yellow).
Extended Data Fig. 3 Salinity, temperature and dissolved oxygen profiles show signatures of melting and mixing below the TEIS.
T–S (a) and DO–S (b) diagrams compare hydrographic data from T1 and T2. Data are colourized after the data shown in Figs. 3 and 4 (with distance along track and for which blue colours denote extremely fresh section) and stars denote locations also called out with stars in Figs. 3 and 4. The warm, salty and oxygen-poor data in red are not shown in Figs. 3 or 4 but come from the outermost data from Extended Data Fig. 2 at distances greater than 10 m from the ice base. This water does not interact with the ice base in the surveyed region. Heavy lines show linear mixing lines between the source water mass responsible for melting the ice base locally (red star) and a pure mixture of GMW or SGW under fully turbulent mixing conditions35,37,42. These may not fully describe sheltered environments along terrace roofs, in which diffusive processes may dominate43,44.
Extended Data Fig. 4 The bathymetry near the GL of the TEIS along the T2 survey is characterized by ridged bedforms of varying wavelengths.
a, Sonar-derived bathymetry from nearest the GL, coloured by depth, showing examples of linear ridges (after Fig. 2, bathymetry and profiles produced with Qimera and projected in QGIS). White lines denote the position of profiles found in c and d. b, Forward-looking sonar shows that the ice-shelf basal topography near the GL (after Fig. 2) is characterized by similar ridges, having an approximately 2.5 m ridge-crest spacing and sloped faces. Forward-looking sonar is projected in Oculus ViewPoint. c,d, Linear profiles of the bed topography across the region show evidence for ridges with approximately 1-m, 2–2.5-m and 5-m wavelengths. These data show that the shape of the ice surface at the GL is inherited from scraping over the bedforms and is later modified into terraces.
Extended Data Fig. 5 Ridged bedforms with pronounced ridge-crest amplitudes are found along the T1 survey.
a, Sonar-derived bathymetry from the borehole to the nearest approach made to the GL, coloured by depth (after Fig. 2, bathymetry and profiles produced with Qimera and projected in QGIS), in which boxes denote the sections shown in b and c. b,c, Close-up views showing details of two regions of the survey. Red (b) and white (c) lines denote the position of profiles found in d and e. d,e, Linear profiles of the bed topography showing that small-scale ridges formed across larger, longer-wavelength topography. f,g, Nearest the GL, 1-m, 5-m and 10-m wavelength along-flow ridges are observed.
Extended Data Fig. 6 Sea-floor topography suggests past dynamics influencing the retreat of Thwaites Glacier.
a, Sonar-derived bathymetry from the borehole to the nearest approach made to the GL, coloured by depth, with callouts for panels b and c (after Fig. 2, bathymetry and profiles produced with Qimera and projected in QGIS). b,c, Close-up views showing details of two regions of the survey, after Fig. 2. Red and white lines indicate the position of profiles found in d–g. d,e, Linear profiles of a crosscutting approximately 3-m-tall sinuous ridge are consistent with a past grounding event allowing enhanced sediment deposition in this area. This is the only such feature in the survey data. f,g, Linear profiles across a possible former subglacial channel near the GL. In f, a 5-m-deep U-shaped trough in the sediment begins parallel to ice flow but then cuts perpendicular to ice flow across lineated bed features and then turns sharply, which could be consistent with a channel incised by subglacial outflow into the sediment. In g, the upstream extent of the trough is less conspicuous, suggesting either modification as the ice ungrounded or that the SGW was not routed discretely through this area.
Extended Data Fig. 7 Bed elevation and ice speed for the TEIS show a changing system susceptible to GL retreat.
a, Colourized bed elevation from BedMachine v3 (ref. 64) for the TEIS is overlaid on a Landsat 8 image with the historical GL positions (coloured lines/zones after ref. 12 are identical to Fig. 1a and Extended Data Fig. 2a, in which green is 2000, white is 2011 and blue is 2016–2017). QGIS map: Landsat 8, 15 m pixel−1, band 8 image LC08_L1GT_003113_20200131_20200211_01_T2_B8, 31 January 2020; the red box denotes the study region. Note that the regions upstream of the present GL are grounded more than 800 m below sea level. b, As in a except coloured by the average 2019 seaward ice-flow speeds for this region from the 120 m pixel−1 ITS_LIVE remote-sensing product66. Note that the flow speeds increase as the ice crosses the GL and decrease near the pinning point.
Extended Data Fig. 8 Topography of terraces under the TEIS demonstrates strongly asymmetric melting and melt processes.
a–d, Images of a terrace upstream of the borehole along T1 show a steep, curved sidewall (a), flat roof (b), sharp transition from the wall to the flat base (c) and close-up of scallops in the wall show differences between modes of melting upward along the roof and base with sideways turbulent melting along the sidewall. Upward-looking views of the base (e) and sidewall (f) of another terrace downstream of the borehole show similar features. Small terraces near the GL along T1 show the initiation of scallops along smaller features in the basal ice (g), in which asymmetric ice melting is clear from the shape and streams of particulates (h,i).
Supplementary information
Supplementary Video 1
Forward-looking video of Icefin’s approach to the GL of the TEIS shows visual evidence of melting and ice–bed interactions. Clear basal ice with embedded pebbles and stones and laminated sediments is observed through the region (video clips from Icefin top forward camera over the last 200 m towards the GL of the TEIS). Variable melting causes particles and pebbles to fall from the ice. The rough, ridged ice base shows topography inherited from scraping along the sea floor as well as the initiation of small, sinuous terraces with scalloped interfaces. At the end of the video, the water column was less than 50 cm thick and the ice is observed resting on the bed in the distance in front of the vehicle.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schmidt, B.E., Washam, P., Davis, P.E.D. et al. Heterogeneous melting near the Thwaites Glacier grounding line. Nature 614, 471–478 (2023). https://doi.org/10.1038/s41586-022-05691-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-05691-0
This article is cited by
-
Tipping point in ice-sheet grounding-zone melting due to ocean water intrusion
Nature Geoscience (2024)
-
Amundsen Sea circulation controls bottom upwelling and Antarctic Pine Island and Thwaites ice shelf melting
Nature Communications (2024)
-
Atlantic Water warming increases melt below Northeast Greenland’s last floating ice tongue
Nature Communications (2024)
-
Seawater oxygen isotopes as a tool for monitoring future meltwater from the Antarctic ice-sheet
Communications Earth & Environment (2024)
-
The variation in basal channels and basal melt rates of Pine Island Ice Shelf
Acta Oceanologica Sinica (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.