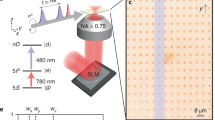
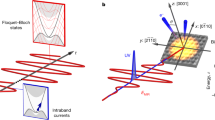
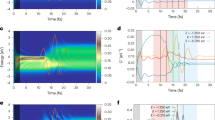
Abstract
Delocalized Bloch electrons and the low-energy correlations between them determine key optical1, electronic2 and entanglement3 functionalities of solids, all the way through to phase transitions4,5. To directly capture how many-body correlations affect the actual motion of Bloch electrons, subfemtosecond (1 fs = 10−15 s) temporal precision6,7,8,9,10,11,12,13,14,15 is desirable. Yet, probing with attosecond (1 as = 10−18 s) high-energy photons has not been energy-selective enough to resolve the relevant millielectronvolt-scale interactions of electrons1,2,3,4,5,16,17 near the Fermi energy. Here, we use multi-terahertz light fields to force electron–hole pairs in crystalline semiconductors onto closed trajectories, and clock the delay between separation and recollision with 300 as precision, corresponding to 0.7% of the driving field’s oscillation period. We detect that strong Coulomb correlations emergent in atomically thin WSe2 shift the optimal timing of recollisions by up to 1.2 ± 0.3 fs compared to the bulk material. A quantitative analysis with quantum-dynamic many-body computations in a Wigner-function representation yields a direct and intuitive view on how the Coulomb interaction, non-classical aspects, the strength of the driving field and the valley polarization influence the dynamics. The resulting attosecond chronoscopy of delocalized electrons could revolutionize the understanding of unexpected phase transitions and emergent quantum-dynamic phenomena for future electronic, optoelectronic and quantum-information technologies.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper. The data supporting the findings of this study are available from the corresponding authors upon request. All other data needed to evaluate the conclusions in the paper are present in the paper or the Methods section.
References
Basov, D. N., Averitt, R. D., van der Marel, D., Dressel, M. & Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 83, 471–541 (2011).
Spencer, J. Learning many-electron wavefunctions with deep neural networks. Nat. Rev. Phys. 3, 458 (2021).
Scappucci, G. et al. The germanium quantum information route. Nat. Rev. Mat. 6, 926–943 (2021).
Basov, D. N., Averitt, R. D. & Hsieh, D. Towards properties on demand in quantum materials. Nat. Mater. 16, 1077–1088 (2017).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Cavalieri, A. L. et al. Attosecond spectroscopy in condensed matter. Nature 449, 1029–1032 (2007).
Schultze, M. et al. Controlling dielectrics with the electric field of light. Nature 493, 75–78 (2013).
Schultze, M. et al. Attosecond band-gap dynamics in silicon. Science 346, 1348–1352 (2014).
Neppl, S. et al. Direct observation of electron propagation and dielectric screening on the atomic length scale. Nature 517, 342–346 (2015).
Sommer, A. et al. Attosecond nonlinear polarization and light–matter energy transfer in solids. Nature 534, 86–90 (2016).
Tao, Z. et al. Direct time-domain observation of attosecond final-state lifetimes in photoemission from solids. Science 353, 62–67 (2016).
Lucchini, M. et al. Attosecond dynamical Franz–Keldysh effect in polycrystalline diamond. Science 353, 916–919 (2016).
Moulet, A. et al. Soft X-ray excitonics. Science 357, 1134–1138 (2017).
Siek, F. et al. Angular momentum-induced delays in solid-state photoemission enhanced by intra-atomic interactions. Science 357, 1274–1277 (2017).
Ossiander, M. et al. Absolute timing of the photoelectric effect. Nature 561, 374–377 (2018).
Kampfrath, T., Tanaka, K. & Nelson, K. A. Resonant and nonresonant control over matter and light by intense terahertz transients. Nat. Photon. 7, 680–690 (2013).
Dhillon, S. S. et al. The 2017 terahertz science and technology roadmap. J. Phys. D. 50, 043001 (2017).
Ciappina, M. F. et al. Attosecond physics at the nanoscale. Rep. Prog. Phys. 80, 054401 (2017).
Seiffert, L. et al. Attosecond chronoscopy of electron scattering in dielectric nanoparticles. Nat. Phys. 13, 766–770 (2017).
Schlaepfer, F. et al. Attosecond optical-field-enhanced carrier injection into the GaAs conduction band. Nat. Phys. 14, 560–564 (2018).
Volkov, M. et al. Attosecond screening dynamics mediated by electron localization in transition metals. Nat. Phys. 15, 1145–1149 (2019).
Heide, C. et al. Attosecond-fast internal photoemission. Nat. Photon. 14, 219–222 (2020).
Hui, D. et al. Attosecond electron motion control in dielectric. Nat. Photon. 16, 33–37 (2022).
Hohenleutner, M. et al. Real-time observation of interfering crystal electrons in high-harmonic generation. Nature 523, 572–575 (2015).
Zaks, B., Liu, R. B. & Sherwin, M. S. Experimental observation of electron–hole recollisions. Nature 483, 580–583 (2012).
Langer, F. et al. Lightwave-driven quasiparticle collisions on a subcycle timescale. Nature 533, 225–229 (2016).
Schmidt, C. et al. Signatures of transient Wannier–Stark localization in bulk gallium arsenide. Nat. Commun. 9, 2890 (2018).
Reimann, J. et al. Subcycle observation of lightwave-driven Dirac currents in a topological surface band. Nature 562, 396–400 (2018).
Vampa, G. et al. All-optical reconstruction of crystal band structure. Phys. Rev. Lett. 115, 193603 (2015).
Borsch, M. et al. Super-resolution lightwave tomography of electronic bands in quantum materials. Science 370, 1204–1207 (2020).
Costello, J. B. et al. Reconstruction of Bloch wavefunctions of holes in a semiconductor. Nature 599, 57–61 (2021).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Zhou, Y. et al. Bilayer Wigner crystals in a transition metal dichalcogenide heterostructure. Nature 595, 48–52 (2021).
Kira, M. & Koch, S. W. Semiconductor Quantum Optics (Cambridge Univ. Press, 2012).
Almand-Hunter, A. E. et al. Quantum droplets of electrons and holes. Nature 506, 471–475 (2014).
Poellmann, C. et al. Resonant internal quantum transitions and femtosecond radiative decay of excitons in monolayer WSe2. Nat. Mater. 14, 889–893 (2015).
Xu, X., Yao, W., Xiao, D. & Heinz, T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014).
Langer, F. et al. Lightwave valleytronics in a monolayer of tungsten diselenide. Nature 557, 76–80 (2018).
Meierhofer, M. et al. Interferometric carrier-envelope phase stabilization for ultrashort pulses in the mid-infrared. Preprint at https://arxiv.org/abs/2207.10073 (2022).
Kira, M. & Koch, S. W. Many-body correlations and excitonic effects in semiconductor spectroscopy. Prog. Quantum Electron. 30, 155–296 (2006).
Kira, M. Coherent quantum depletion of an interacting atom condensate. Nat. Commun. 6, 6624 (2015).
Kira, M. & Koch, S. W. Quantum-optical spectroscopy in semiconductors. Phys. Rev. A 73, 013813 (2006).
Fang, S. et al. Ab initio tight-binding Hamiltonian for transition metal dichalcogenides. Phys. Rev. B 92, 205108 (2015).
Vanderbilt, D. Berry Phases in Electronic Structure Theory: Electric Polarization, Orbital Magnetization and Topological Insulators (Cambridge Univ. Press, 2018).
Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 40, 749–759 (1932).
Heide, C. et al. Probing electron-hole coherence in strongly driven 2D materials using high-harmonic generation. Optica 9, 512–516 (2022).
Nagai, K. et al. Effect of incoherent electron-hole pairs on high harmonic generation in atomically thin semiconductors. Preprint at https://arxiv.org/abs/2112.12951 (2021).
Acknowledgements
We thank K.-Q. Lin, H. Petek and N. Hofmann for assistance and helpful discussions. The work in Regensburg has been supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through Project ID 422 314695032-SFB 1277 (Subproject A05) as well as Research Grant HU1598/8. Work in Ann Arbor has been supported by ARO through Award W911NF1810299, W.M. Keck Foundation and College of Engineering Blue Sky Research Program.
Author information
Authors and Affiliations
Contributions
M. Kira and R.H. conceived and supervised the study. J.F., M.M., D.A., C.P.S. and R.H. carried out the experiment and analysed the data. F.S., M.L., A.G. and M. Knorr provided, processed and characterized the samples. M.B. and M. Kira developed and performed the many-body computations and analysed the data. J.F., M.B., M. Kira and R.H. wrote the manuscript with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review information
Peer review information
Nature thanks Michael Sentef, Liang Luo and Koichiro Tanaka for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Schematic of the experimental setup.
a, The 8.6-fs-NIR pulse train is split into two branches. The first one passes a quarter wave plate (λ/4) and is overlapped with the THz field with an indium tin oxide-coated window (ITO) before both pulses are focused onto a GaSe crystal for EOS or the WSe2 sample to generate HSB. The remaining excitation light and the emerging HSB radiation are collimated and separated from the THz radiation with a germanium wafer (Ge). With a dichroic mirror (DM), the HSB radiation is sent into a spectrometer (CCD), while the polarization state of the transmitted NIR pulse can be analysed by a quarter wave plate, a Wollaston prism (W), and a balanced pair of photodiodes (BPD). The remaining THz field is overlapped with the second NIR branch to constantly monitor the electro-optic signal (EOM). b, Measured SHG-FROG spectrogram and c, reconstructed temporal shape of the NIR light with a pulse duration of 8.6 fs. d, Comparison between excitation spectrum (orange) and absorbance (blue) of monolayer WSe2. The high-energy edge of the excitation spectrum is chosen to be resonant with the monolayer 1s transition. e, Waterfall plot of successive EOS measurements with the reference beam line. The electric field of the reference THz waveform corresponds to the colour scale. Fitting the temporal position of the recorded transients reveals a standard deviation of only σ = 84 as, attesting to the excellent stability of the setup during a measurement.
Extended Data Fig. 2 Identifying monolayer and bulk WSe2.
a, Optical microscopy picture of the exfoliated sample on a diamond substrate. The monolayer part of the WSe2 crystal is indicated by the red dashed line. Circles (diameter corresponds to the NIR spot size in focus) show the spots used for the monolayer (blue) and bulk (orange) measurements presented in the main text. b, Photoluminescence (red colour map) and transmission (blue colour map) of the sample using a continuous-wave laser with a centre wavelength of 532 nm. c, Schematic cross-section of the WSe2 sample consisting of a bulk and monolayer (ML) part next to each other on a diamond substrate. The incident light (NIR and THz) hits the sample from the WSe2 side. Remaining NIR and THz radiation as well as the emitted HSB radiation are transmitted through the diamond substrate.
Extended Data Fig. 3 Dependence of the subcycle delay on the sample thickness.
Measured subcycle delay δsc and its standard error for different spots on the WSe2 sample with Epeak = 6.2 MV cm−1 and ΦNIR = 12 μJ cm−2. 60 nm (orange) and 25 nm (purple) thick areas of the crystal yield the same averaged value ⟨δsc⟩ (dashed line) within the averaged margin of error (shaded area).
Extended Data Fig. 4 Data analysis and calculation of error bars.
a, Recorded transient before (orange solid line) and after (blue solid line) a single scan of the HSB spectrogram. The inset shows a close-up of a field zero-crossing, revealing a shift of 130 as of the driving field during a measurement. b, Spectrally integrated trace of a single HSB scan as recorded (orange) and after compensation of the temporal drift (blue). Its time axis is stretched or squeezed (blue) in accordance with the temporal shift correction in a. Insets: Zoom-in on IHSB illustrating the drift compensation for early (left panel) and late (right panel) injection times. c, e, Peaks of the corrected HSB emission (orange spheres) are fitted using Gaussian (c) or quadratic (e) functions (orange solid lines) in a small temporal window (orange shaded area) to determine their exact temporal position. The subcycle delay, δsc, is calculated as the timing difference between IHSB and ETHz (grey) peaks. Inset in e: histogram of the deviation of the interpolated curve (line) from the raw data (dots), yielding a noise-limited time resolution of 100 as. d, f, Extracted subcycle delay from c and e for four consecutive scans (coloured spheres). By averaging, their mean value (blue spheres) as well as their standard error (indicated by the blue shaded area) are determined.
Extended Data Fig. 5 Synchronized timing of e–h recollisions and HSB emission.
a, Time-resolved computed HSB emission intensity for monolayer (blue line) and bulk (orange line) WSe2. Coherent excitons are created by an 8.6 fs NIR pulse (intensity envelope, red line) at time tex after the peak of the THz field (|ETHz|, grey shaded area). The HSB emission peaks (vertical dashed lines) at \({T}_{{\rm{coll}}}^{{\rm{ML}}}\) = 12.6 fs after the excitation for monolayer and at \({T}_{{\rm{coll}}}^{{\rm{bulk}}}\) = 18.6 fs for bulk WSe2, respectively. b–e, HSB Wigner functions WHSB(x,k) (contours) at times t = 12.6 fs and t = 18.6 fs for monolayer and bulk WSe2. Orange lines show the dynamics of the centroid of the Wigner function.
Extended Data Fig. 6 Predicted HSB intensity as a function of the NIR pulse duration.
Computed HSB intensity IHSB as a function of the NIR excitation time for pulse durations of τNIR = 7.2 fs (dark red line), 8.6 fs (dark blue line), 10 fs (light red line), and 11.5 fs (light blue line). The shaded area denotes the driving field |ETHz| whose three largest peaks are labelled.
Extended Data Fig. 7 HSB spectra for constant dephasing times.
a, Computed HSB spectra of the full QDCE approach (grey shaded area) compared to computations with different constant dephasing times τ (lines). The data are multiplied by a factor of 106 at energies hν > 1.9 eV, for visibility. b, Ratio of the spectrum from the full QDCE computation with each of the constant-dephasing computations. c, Density of coherent excitons as function of time for the full QDCE computation (grey area) and two constant-dephasing calculations with τ = 21.9 fs (red line) and τ = 8.2 fs (blue line) after excitation (orange shaded area, NIR pulse envelope). The vertical dashed lines indicate peak densities.
Extended Data Fig. 8 Role of Coulomb correlations on the subcycle delay.
Computed subcycle delay for bulk (orange) and monolayer (blue) WSe2 as a function of the exciton binding energy resulting from a Coulomb interaction suppressed artificially, while keeping all other parameters fixed. Orange and blue dashed vertical line: exciton binding energy E1s of bulk (E1s = 60 meV) and monolayer (E1s = 295 meV) WSe2, respectively. The arrow marks the subcycle-delay shift of 2.1 fs due to increased excitonic binding.
Source data
Rights and permissions
Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Freudenstein, J., Borsch, M., Meierhofer, M. et al. Attosecond clocking of correlations between Bloch electrons. Nature 610, 290–295 (2022). https://doi.org/10.1038/s41586-022-05190-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-05190-2
This article is cited by
-
Light-wave-controlled Haldane model in monolayer hexagonal boron nitride
Nature (2024)
-
Raman time-delay in attosecond transient absorption of strong-field created krypton vacancy
Nature Communications (2024)
-
Lightwave electronics in condensed matter
Nature Reviews Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.