Abstract
When electric conductors differ from their mirror image, unusual chiral transport coefficients appear that are forbidden in achiral metals, such as a non-linear electric response known as electronic magnetochiral anisotropy (eMChA)1,2,3,4,5,6. Although chiral transport signatures are allowed by symmetry in many conductors without a centre of inversion, they reach appreciable levels only in rare cases in which an exceptionally strong chiral coupling to the itinerant electrons is present. So far, observations of chiral transport have been limited to materials in which the atomic positions strongly break mirror symmetries. Here, we report chiral transport in the centrosymmetric layered kagome metal CsV3Sb5 observed via second-harmonic generation under an in-plane magnetic field. The eMChA signal becomes significant only at temperatures below \({T}^{{\prime} }\approx \) 35 K, deep within the charge-ordered state of CsV3Sb5 (TCDW ≈ 94 K). This temperature dependence reveals a direct correspondence between electronic chirality, unidirectional charge order7 and spontaneous time-reversal symmetry breaking due to putative orbital loop currents8,9,10. We show that the chirality is set by the out-of-plane field component and that a transition from left- to right-handed transport can be induced by changing the field sign. CsV3Sb5 is the first material in which strong chiral transport can be controlled and switched by small magnetic field changes, in stark contrast to structurally chiral materials, which is a prerequisite for applications in chiral electronics.
Similar content being viewed by others
Main
The role that symmetries play in determining the properties of matter can hardly be overstated. Two opposite extremes are particularly interesting in crystalline solids. Higher symmetries constrain emergent degrees of freedom to mimic free particles—creating, for instance, massless Dirac or Weyl fermions that recover, at low energies, almost the full Lorentz group of free space11,12,13,14. A second approach is to study low-symmetry systems with novel responses. Among these, asymmetric systems characterized as ‘chiral’ play a special role across biology, chemistry and physics15,16. Crystals are structurally chiral if they possess no mirror, inversion or roto-inversion symmetry, giving rise to left- and right-handed enantiomers. This chirality can be imprinted on the crystals’ emergent excitations, which are then also characterized by a definite handedness. The interaction between structural chirality and the breaking of time-reversal symmetry (TRS) is of particular interest, as it links the static chirality to temporal processes, such as growth, catalysis and wave propagation17. Response functions that jointly arise because of chirality and TRS breaking are called magnetochiral anisotropies18. Specifically, in metals, one studies the electronic magnetochiral anisotropy (eMChA), which opens up possibilities to detect, manipulate and utilize chiral properties in electronics1,2,3,4,5,6.
eMChA usually refers to a change in resistance R due to an applied current I and external magnetic field B that is conventionally expressed as R(B,I) = R0(1 + μ2B2 + γ±B⋅I)1 (see Fig. 1). Time-reversal symmetry in non-magnetic metals enforces a magnetoresistance even in-field, which usually takes the semi-classical form μ2B2, with μ being the mobility. The scalar product B⋅I is only allowed in chiral crystals without space-reflection symmetries, and hence eMChA appears. Its strength is described by the coupling constant, γ±, which takes opposite sign for the two enantiomers and is tensorial in anisotropic conductors. eMChA is most commonly detected by the associated second-harmonic voltage generation under low-frequency a.c. currents, 4V2ω/Vω = ΔR/R, where ΔR = R(B,I) − R(B,−I) denotes the odd in-current and R = R(B,I) + R(B,−I) denotes the even in-current contribution to the resistivity.
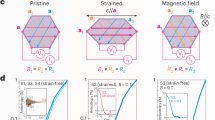
a, Illustration of electrical resistance of normal and chiral conductors within the low-frequency limit. b, I(V) curve for a chiral conductor. In a d.c. measurement (left), the measured voltage displays a non-linear current dependence with magnetic field applied. In the a.c. case (right), the field-induced second-harmonic voltage, V2ω, depends quadratically on the a.c. current Iω. c, Different mechanisms for electronic magnetochiral anisotropy. The blue dashed line in the crystalline structure case represents the notation of helical atomic chains. For the case of scattering, the encircled hands represent the scattering centres with particular chirality. d, The crystal structure of CsV3Sb5 preserves all mirror symmetries at high temperatures and only spontaneous symmetry breaking at low temperatures enables a finite eMChA in a symmetric microstructure.
To display eMChA, a conductor must break inversion symmetry, which can occur as a weak effect in any metal when its macroscopic shape is chiral2,3, for example, in a coil (Fig. 1). Alternatively, materials with chiral crystal structure1,4 generally show eMChA in any conductor shape. We note that the ‘chiral electronic structure’ of the symmetry-broken phase mentioned here does not necessarily have to have the symmetries of a chiral space group. In a layered, quasi-two-dimensional compound one refers to a structure as ‘chiral’ when the in-plane mirror symmetries are broken, whereas the Mz mirror symmetry might still be intact. However, this lack of in-plane mirror symmetry is enough to enable the observation of eMChA in the geometry of our measurements. eMChA expresses an imbalance between scattering processes of different handedness, which can occur either from the intrinsic handedness of the carriers in chiral crystals, or extrinsically from chiral defects, as in plastically twisted conductors. When electronic interactions form ordered phases within chiral materials, as, for example, in chiral magnets, eMChA can be further amplified via scattering off, for example, an emergent chiral spin texture5,6.
In this work, we demonstrate eMChA in a rectangular bar of CsV3Sb5, a layered metal in which vanadium atoms form kagome nets. In this system, a cascade of correlated symmetry-breaking electronic phases emerges at low temperatures7,10,19,20,21,22, including a charge-density wave (CDW) state below TCDW ≈ 94 K and superconductivity below Tc ≈ 2.5 K (refs. 19,23,24,25,26,27). Experimental evidence mounts for a further transition within the charge-ordered phase at \({T}^{{\prime} }\approx 35\) K, accompanied by an additional 4a0 unidirectional ordering vector7 and time-reversal symmetry breaking8,9,10. The sudden onset of unexpectedly strong chiral transport at \({T}^{{\prime} }\) is our main observation. Crucially, this system is centrosymmetric at high temperatures, yet the relevant mirror symmetries are spontaneously broken by correlated phases of the itinerant carriers (Fig. 1). Reversible chirality of the electronic structure within the CDW phase has been observed in scanning tunnelling microscopy (STM) experiments28. Note that the accompanying crystal distortion is so weak that the low-temperature crystal structure remains actively debated7,24,29,30. In contrast to structurally chiral crystals that strongly differ from their mirror image, here the differences between the enantiomers are subtle and test the limits of experimental resolution. Hence, the observation of eMChA itself in this compound points to its novel origin. As a consequence, the material’s chirality itself can be switched, which leads to field-switchable chiral transport in CsV3Sb5.
To truly obtain symmetry lowering from spontaneous symmetry breaking, it is critical to avoid any accidental strain fields that may break the symmetry explicitly. To do so, we decouple the crystalline bar mechanically as much as possible from its supporting substrate31 (Fig. 2a). This structure is mechanically supported by gold-coated SiNx membrane-based (200 nm thick) springs, and the differential thermal contraction strain is estimated to be less than 20 bar. Any signatures of chiral transport vanish in a reference experiment with even modest strain fields caused by stiff substrate coupling (see Methods), evidencing a strong coupling between the charge order and lattice distortions, which is not surprising in CDW systems32. This provides a natural explanation for the opposing STM experiments28,33.
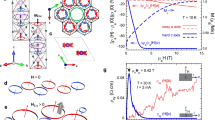
a, Low-strain microstructure fabricated by focused ion beam. b, Field dependence of second-harmonic voltage with current applied along the z(c) axis. The signal becomes sizeable when the magnetic field is applied approximately in the plane. The inset sketches the transport bar. c, The red continuous line in the left panel represents temperature dependence of ΔV2ω = V2ω(18 T) − V2ω(−18 T) with the magnetic field applied approximately in the plane. The blue open circles show the Fourier transform intensity of the wavevector corresponding to the 4a0 unidirectional charge-order phase adopted from ref. 7, and the green squares represent the anomalous Nernst effect reported in ref. 34. The right panel displays log-scale temperature dependence of ΔV2ω and magnetoresistance ratio MR = (ρc(18 T) − ρc(0))/ρc(0), where ρc(0) denotes the resistivity at zero field.
Observation of eMChA in CsV3Sb5
Our main observation is the appearance of a sizeable second-harmonic response, V2ω, to a low-frequency transport current (7 Hz), which clearly evidences the diode-like behaviour due to chiral transport within the charge-ordered state at low temperatures (Fig. 2). First, we discuss out-of-plane currents under an approximately in-plane magnetic field, which is purposely misaligned by 0.5° with respect to the kagome planes. At zero field and T = 5 K, just above the superconducting transition, no second harmonic is observed, yet the signal quickly grows with increasing magnetic field. Its field dependence is well described by V2ω ∝ B3 up to 18 T, the highest fields accessible to the experiment. This is a striking departure from the behaviour of structurally chiral materials, such as α-Te (ref. 1), where V2ω displays a linear field dependence, ΔR/R = γ±B⋅I (ref. 1). This suggests that the magnitude of eMChA itself is field dependent, given by γ±(B).
eMChA depends on the relative direction of the field and the current, and hence, even in a non-linear scenario, V2ω(B) must change sign when the field polarity reverses, as is observed experimentally. This antisymmetric field dependence provides strong evidence against a putative thermal origin of second-harmonic voltage generation by Joule heating, as the linear magnetoresistance is even in the magnetic field (see Methods). Pronounced quantum oscillations are also observed above B = 10 T, demonstrating an influence of Landau quantization on eMChA. This behaviour is observed consistently in two devices with different mechanical mounting approaches, rendering potential torque artefacts due to the soft-mounted structure unlikely. An identically shaped sample probing in-plane transport does not show second-harmonic generation at any field configuration, demonstrating that eMChA is only relevant in the interplane transport (see Methods).
To further characterize eMChA and elucidate its origin in this nearly centrosymmetric material, we next turn to the temperature dependence of V2ω. Figure 2b displays the raw V2ω(B) without antisymmetrization. Yet, at elevated temperatures the weak thermal second-harmonic generation can obscure the chiral transport signatures; therefore, we focus on the antisymmetric component ΔV2ω = V2ω(18 T) − V2ω(−18 T) (see Methods for full data). At high temperatures above TCDW, no ΔV2ω is observed, as expected. The transition into the CDW state is clearly evident as a sharp spike in ΔV2ω at TCDW, which we associated with the non-analyticity of R(T). A continuous antisymmetric second-harmonic signal only emerges at temperatures below 70 K. Its slow increase with decreasing temperature suddenly accelerates at \({T}^{{\prime} }\approx \) 35 K, which is apparent as a change in slope on the logarithmic scale. At lower temperatures, ΔV2ω increases significantly and saturates at its maximum value below 3 K. Although our observations only evidence the absence of chiral scattering and do not exclude a chiral order at TCDW that merely does not affect transport, our results are suggestive of a secondary transition or crossover at lower temperatures of \({T}^{{\prime} }\). In particular, this temperature dependence agrees well with both the Fourier transformation intensity of the 4a0 CDW vector (q4a0) obtained from STM experiments7 and the large anomalous Nernst effect34. Such correspondence demonstrates the direct connection between the unidirectional charge order, electronic chirality and hidden magnetic flux. This consistency is further supported by the results of muon-relaxation experiments, which suggest the onset of TRS breaking at around 70 K and a subsequent rearrangement of local field distribution at 30 K (refs. 8,9,10).
Field-switchable electronic chirality
The unusual nature of the eMChA in CsV3Sb5 becomes apparent when the field orientation is varied with respect to the kagome planes (θ = 0° denotes the in-plane field orientation; Fig. 3). No V2ω is observed at large field angles (θ > 10°). Only within a narrow angle range, θ = ±10°, does V2ω quickly grow as the field-angle approaches θ = 0°. It reaches a maximum around θ ≈ 0. 5°, the configuration discussed previously in Fig. 2. For smaller θ, V2ω rapidly decreases and vanishes for fields within the kagome planes (θ = 0°). On further rotation, to small negative θ, the signal repeats but with the opposite sign. This marks a most striking aspect of the data: tilting the field across the kagome nets changes the handedness of the material. Rotating the field by 1° barely changes B, hence an abrupt sign change of V2ω implies a transition into the opposite enantiomer. Furthermore, the signal’s magnitude strongly reduces on raising the temperature or lowering the field strength, whereas the angular extent and the sharp anomaly at the in-plane field persists. At temperatures above 35 K the peak is hardly observable, and the faint residual anomaly reflects the exponential drop of V2ω above \({T}^{{\prime} }\) (Fig. 2d). The rotation curves are slightly hysteric; however, given the sharpness of the steep transition, it was impossible to distinguish an intrinsic hysteresis from the mechanical backlash of the rotator.
a, Angular dependence of V2ω for I∥a and I∥c. A sharp spike with sudden sign reversal within 0.5° is observed for I∥c around the a axis. b,c, Angular dependence of V2ω at various temperatures with B = 18 T (b) and of various magnetic fields at T = 2 K (c). d, Field-dependent eMChA coefficients at various angles. The inset displays the magnetoresistance measured with current applied along the c axis at various field directions.
The possibility and ease of magnetic manipulation of the electronic chirality presents a unique electromagnetic response of CsV3Sb5. It suggests that the low-temperature state differs from a simple chiral charge redistribution, as observed, for example, in the 3q chiral CDW35 state of TiSe2. Such a static charge redistribution only couples to magnetic fields via higher order interactions, and its involved lattice response renders it unlikely to be easily manipulated at temperatures well below TCDW. Instead, the experimental situation in CsV3Sb5 points to coupled TRS breaking, including the concomitant magnetic anomalies at TCDW, the field tunability, as well as muon spectroscopy experiments8,9. As a microscopic picture for this correlated state, an orbital loop-current phase in the kagome planes has been proposed, which is consistent with these experimental observations22,36,37.
Analysis of eMChA strength
Despite its exotic properties, the eMChA in CsV3Sb5 can be rationalized within the existing theoretical framework. The magnetoresistance of CsV3Sb5 is approximately linear in B for small angles θ at high magnetic fields (see inset of Fig. 3d). Such behaviour is indeed not unexpected for a material with density-wave order38 and has also been observed in many semimetals39,40. This marks a crucial difference to previous eMChA studies, in which the conventional resistance R(B,I) + R(B,−I) ≈ 2R0 remains approximately field independent. This, and the strong θ dependence of the eMChA coefficient γ, means that eMChA cannot be characterized by a constant tensor, as is common practice in the literature for conventional eMChA materials. Yet, we can gain some insights about the magnitude of eMChA by computing ΔR/(R∣B∣∣J∣) = 4V2ω/(Vω∣B∣∣J∣) for given magnetic field strength |B| and current density J (see Fig. 3d)1, for quantitative comparisons to other systems. The quantity ΔR/(R∣B∣∣J∣)equals the constant γ when it is a field-independent parameter in chiral materials commonly used in the literature. At B = 18 T and θ = 0.5° we find ΔR/(R∣B∣∣J∣) ≈ 2.4 × 10−11 m2 T−1 A−1. In comparison, this value is smaller than its record observations in t-Te (ref. 1) (10−8 m2 T−1 A−1) and TTF-ClO4 (ref. 4) (10−10 m2;T−1 A−1), for which the distinct structural chirality results in relatively large eMChA, whereas it is larger than that of chiral magnets, such as CrNb3S6 (ref. 5) (10−12 m2 T−1 A−1) and MnSi (ref. 6) (10−13 m2 T−1 A−1), in which the chiral spin texture plays a major role in eMChA.
As the conventional eMChA analysis is only applicable for materials with negligible magnetoresistance, a description in terms of the conductance is more appropriate to further capture the lowest order field-tuned behaviour of the response in CsV3Sb5 (see Methods). For purely longitudinal transport and negligible Hall resistivity, the conductance is the inverse of the resistance, such that in analogy to the usual analysis of eMChA, for the conductance we write σ + Δσ ≈ 1/R − ΔR/2R2 (see Methods). We can thus extract \(\Delta \sigma \propto {V}_{2}\omega \,/\,{V}_{\omega }^{2}\), where Vω is now linear in B for large fields. For a field applied approximately in-plane, Δσ is thus approximately linear in B, which is the lowest order coupling between magnetic field and current (see Methods) and naturally explains the B3 dependence of V2ω. The linear field dependence of Δσ yields a field-independent first-order derivative ∂(Δσ)/∂B (see Fig. 4). The sudden sign reversal of ∂(Δσ)/∂B for small θ then suggests that the out-of-plane component of the field, Bz, has a non-perturbative effect on the system and we treat it separately, whereas the in-plane component is a perturbation to linear order. In other words, we write \(\Delta \sigma ({\bf{B}},{I}_{z})=\widetilde{\sigma }({B}_{z}){B}_{x}{I}_{z}\). Note that such a coupling is only allowed for a system that breaks the y ↦ −y mirror symmetry. With Δσ(B,Ix) vanishingly small, no similar conclusion can be drawn for the mirror symmetry z ↦ −z.
a, Field dependence of chiral conductivity Δσ at various angles. Between θ = ±0.3 and ±4.8° all data are measured with an angle step of 0.5°. b, Angular dependence of the first-order derivative ∂(Δσ)/∂B from B = 6 to 18 T. The green curve represents the model description of chiral conductivity: \(\frac{\partial \Delta \sigma }{\partial B}={\rm{sign}}(\theta )\,\cos (\theta )\,\frac{{\Delta }_{0}\,\widetilde{M}{e}^{2}\tau }{2{{\rm{\pi }}}^{3}\hbar }\), as derived in the Methods. c, Sketch of a chirality reversal at in-plane aligned magnetic fields. The emergence of opposite domains can naturally lead to a strong enhancement of eMChA at low field angles.
Theoretical modelling
The behaviour of Δσ seen in our experiment demonstrates that the charge order in CsV3Sb5: (1) breaks in-plane mirror symmetries, at least below \({T}^{{\prime} }\approx \) 35 K and (2) can be manipulated by an out-of-plane magnetic field in the same temperature regime. We thus establish that the tunability of the chirality of charge order in CsV3Sb5, previously seen in STM experiments, is a macroscopic bulk property of the unconventional charge order.
We further propose the following qualitative scenario, which would be consistent with the full θ dependence of our experimental observations and calls for confirmation by local-probe techniques (Fig. 4). Bz is the natural tuning parameter in kagome-net physics, as evidenced by our experiments as well as STM experiments. Akin to a soft ferromagnet, large values of Bz (large θ) induce a fully polarized, monochiral state. In this polarized state, only intrinsic chiral scattering processes induce eMChA, which commonly are weak. As the field is tilted towards the plane, Bz is reduced and domains of opposite chirality appear, which act as ideal chiral scattering centres. Hence, domain-wall scattering leads to strong extrinsic eMChA. Naturally, a local probe, such as STM, would observe a chiral structure and occasionally the required domain boundaries between them, as indeed is the experimental situation28,33. At even smaller Bz for fields very close to the planes, both chiralities appear symmetrically and hence a globally averaging probe, such as transport, observes a macroscopically symmetric conductor with vanishing eMChA. A fully symmetric process appears if the field is turned further, yet with inverted roles of majority and minority chirality.
In this scenario, the chirality switching is driven by Bz independent of the in-plane field, in particular it would also occur for fully out-of-plane fields, where no eMChA is observed in our experiment. Yet, unlike structurally chiral systems, here the magnetic field plays a dual role. Whereas Bz sensitively changes the sign of ∂(Δσ)/∂B, the large in-plane field is essential to observe finite eMChA, as Δσ ∝ Iz∣B∣. Given the close relationship between the field-switchable chiral transport and the chiral domains in CsV3Sb5, it is worth exploring its generality in other materials with suspected chiral orbital loop current.
Outlook
Although the small magnitude and extreme environmental conditions probably preclude direct applications of CsV3Sb5, it showcases that spontaneous symmetry breaking can be used to transform small changes in external fields into singular changes in the response functions of chiral conductors. Given the subtle deviation from centrosymmetry of the charge-ordered phase, the emergence of eMChA in correlated states calls for new theoretical approaches to identify the microscopic mechanisms. The multitude of competing ground states in correlated materials gives rise to their versatility and tunability, which now presents a new approach towards chiral transport. In this direction, the field-switchable chiral transport adds a new aspect to the emergent picture of a highly frustrated, strongly interacting electron system on the kagome planes of CsV3Sb5. Although the magnitude of eMChA is unexpectedly large, these results link well with recent works that have shown the charge-ordered state to be chiral and TRS breaking 8,9,10,28. Akin to the theme of coupled orders in multiferroics, a series of new response functions emerges in materials such as CsV3Sb5, with multiple intertwined order parameters.
Methods
Crystal synthesis and characterization
CsV3Sb5 crystallizes in the P6/mmm space group, which features a layered structure of kagome planes formed by the V atoms (Extended Data Fig. 1). The single crystals were grown by the self-flux method24. Hexagonal plate-shaped crystals with typical dimensions of 2 × 2 × 0.04 mm3 were obtained. The crystals were characterized by X-ray diffraction off the maximum surface on a PANalytical diffractometer with CuKα radiation at room temperature. As shown in Extended Data Fig. 1, all the peaks in the X-ray diffraction pattern can be identified as the (00l) reflections of CsV3Sb5.
On the basis of the crystalline structure, we have calculated the band structure of CsV3Sb5 by density functional theory using the Quantum Espresso package41, the details of which can be found in ref. 31. The obtained electronic structure features multiple Dirac nodal lines lifted by spin-orbit coupling, leaving only symmetry-protected Dirac nodes at L points. These results are consistent with previous reports23,24.
Magnetoresistivity measurements were performed with electric current and magnetic field applied along out-of-plane (z) and in-plane (x) directions, respectively. The magnetoresistance displays a quasi-linear field dependence up to B = 18 T, whereas Hall resistivity is almost negligible compared with that. This is expected, as the electrical current is applied along the out-of-plane direction the Hall resistivity should vanish for such a quasi-two-dimensional material, with the Brillouin zone dominated by the large cylindrical Fermi surfaces.
Angular dependence of magnetoresistance and its relation to V 2ω
At low temperature, angle-dependent magnetoresistivity displays a strong peak when the magnetic field direction rotates across the kagome plane (Extended Data Fig. 2). With increasing temperature this peak gradually transitions to a broad hump at T = 50 K. This strong enhancement of magnetoresistivity at in-plane fields is probably a feature of open-orbit magnetotransport, which is expected for a metal featuring cylindrical Fermi-surface sheets42. The smearing of the spike at high temperatures therefore demonstrates the reduction of carrier mobility with increasing temperature.
In the meantime, the strong increase of magnetoresistivity naturally leads to enhancement of V2ω. Combining the angular dependence of both leads to a clear quadratic relationship between V2ω and ρc, which provides further evidence for the chiral conductance analysis.
I–V characteristics of eMChA
Second-harmonic voltage generation due to eMChA is expected to display a quadratic current dependence. Here we present the I–V characteristics of both first- and second-harmonic voltages measured with a 7 Hz a.c. current (Extended Data Fig. 3). For Vω the relationship depends linearly on current, which corresponds to the first-order resistance term. On the other hand, the second-harmonic voltage shows a clear quadratic current dependence, which is an expected signature of eMChA. These results again demonstrate that the observed V2ω originates from the chiral correction of conductivity due to the electronic chirality of CsV3Sb5.
Examination of Joule heating effect
Joule heating is a natural extrinsic origin of higher harmonic voltage generation43,44. Applying an a.c. electric current, Iω, must result in an oscillating temperature with a frequency of 2ω. Therefore if the electrodes of the device are strongly imbalanced in contact resistance, an extrinsic V2ω can be observed. To further check the influence of Joule heating in the measurements of eMChA in CsV3Sb5, we performed systematic current-dependent V2ω measurements under different thermal conditions (Extended Data Fig. 4). By controlling the helium gas pressure of the sample space, the thermal link between the device and the sample chamber can be easily tuned. Within a low current regime (below 0.12 mA), the collapse of all curves measured at different conditions suggest the insignificance of the Joule heating effect. With further increasing current, Joule heating inevitably grows and becomes detectable. To avoid any disturbance due to Joule heating, all measurements of eMChA have been performed with a relatively low a.c. current of 0.1 mA and high gas pressure (ps ≈ 600 mbar) of the sample space, providing the maximal cooling power.
Reproducibility of eMChA with two different devices
To show the reproducibility of the second-harmonic voltage generation due to eMChA in CsV3Sb5, we have measured two membrane-based devices with different mounting techniques/geometries (Extended Data Fig. 5). For device S1, the sample was completely suspended by soft Au-coated membrane springs. In comparison, device S2 was attached to the membrane only on one side, and the other side of the sample was welded directly to the Si substrate by focus ion beam (FIB)-assisted Pt deposition. Device S2 displays a slightly broader CDW transition than S1 in the temperature dependence of resistivity across TCDW, yet the transition temperatures are exactly the same. This suggests a marginally larger strain gradient across the device due to thermal contraction for device S2, which is compatible with the estimated strain value presented in the next section. The second-harmonic voltage was consistently observed among the two devices, with a similar value as well as an almost identical angular spectrum. These results demonstrate the clear consistency among different low-strain samples, and therefore evidence that the observed eMChA in CsV3Sb5 is an intrinsic material property. These devices further differ in their coupling strength between the substrate and the device. In view of the much stiffer coupling in S2, the similarity of the data speaks against magnetic torque induced angle changes as a putative error source.
Estimation of strain due to differential thermal contraction
To obtain the tensile strain applied to the sample, we first need to estimate the total displacement of the samples and substrates used due to different thermal contraction coefficients. On cooling from 300 K to 4 K, the integrated thermal contraction coefficients of SiNx (εSiN) and Si (εSi) were 0.0342% and 0.0208%, respectively. For the sample itself we assumed a typical thermal contraction coefficient for alkali metal of εSample ≈ 0.1%, which provides a conservative, upper bound. On the basis of these parameters and the actual device geometry illustrated in Extended Data Fig. 6, the total displacement can be easily obtained as:
The spring constant of the SiNx spring for device S1 is estimated as 125 N m−1 from finite element simulations31 (COMSOL), the total pressure can be calculated as:
where A is the cross-section of the spring.
Meanwhile, for device S2, the pressure can be calculated using the same process:
In both cases the pressure is less than 20 bar. Taking the typical Young’s modulus of alkali metals (≈5 GPa), the strain applied on the sample is estimated to be ≈0.04%, which quantifies the low-strain nature of these devices.
Strain effect on eMChA
The necessity of low-strain mounting was revealed by a comparative study of device S4, which features a sample that is glued down to a sapphire substrate. Here the device is structured into an L shape with two long beams along both the a and c directions (Extended Data Fig. 7). As the sample and substrate are mechanically coupled via the glue droplet, the thermal contraction difference between them results in a tensile strain along the beam direction. This tensile strain not only shifts the CDW transition of device S4 to a higher temperature compared to the strain-free S1, but also suppresses the superconducting transition down to lower temperatures. Most importantly, no meaningful second-harmonic voltage has been observed for device S4. These observations suggest the importance of c axis tensile strain, which in defining an extrinsic, long-range domain structure, is unable to be switched or tuned. This observation suggests that residual strain fields would provide a natural explanation for the contradictory STM experimental results28,33.
Field-symmetry analysis of second-harmonic voltage
To further demonstrate the origin of second-harmonic voltage generation, we also measured the temperature-dependent V2ω at B = 18 and −18 T (Extended Data Fig. 8). By taking the sum and difference of these two results we obtained both the field-symmetric and -asymmetric components of V2ω. It is clear that the antisymmetric component dominates the total signal at low temperatures, whereas the symmetric component, which is probably due to Joule heating at the electric contacts, is merely a minor part.
Theoretical considerations
In this section, we discuss the magnetoresistance of a single-band model to illustrate the appearance of the various contributions to the linear magnetoresistance, and to the second-order response discussed in the main text. In particular, we are interested in the effect of a CDW on the magnetotransport, when the CDW not only breaks translation, but also breaks time-reversal and several mirror symmetries. Note that we focus here on intrinsic contributions that enable us to explain the abrupt switching of the second-order response at small θ. To model the full θ dependence, extrinsic contributions would have to be included as well, as discussed in the main text.
In most metals, the transverse magnetoresistance scales quadratically with magnetic field, \({\rho }_{zz}({B}_{x})\propto {B}_{x}^{2}\). However, this behaviour can change to linear with B if there are small Fermi surfaces or Fermi surfaces with sharp corners45. Although the conditions for such B-linear behaviour are probably not satisfied in the normal state of CsV3Sb5, the Fermi-surface reconstruction due to the CDW instability is expected to result in new, smaller Fermi surfaces, such that a linear magnetoresistance, as observed, can be explained. Note that linear magnetoresistance in density-wave materials has indeed been observed and discussed in the context of Fermi-surface reconstruction by Feng and co-workers38.
When the density-wave instability breaks additional symmetries, we find further contributions to the magnetoresistance, or, equivalently, to the conductivity. To see this, we use Boltzmann transport theory in the relaxation-time approximation, in which the conductivity is given by
with e the electron charge, τ the scattering time and
the velocity for electrons with dispersion ξk. We assume in the following that we are in the symmetry-broken charge-ordered phase and the dispersion is given by \({\xi }_{{\bf{k}}}^{{\rm{CDW}}}\) at zero magnetic field. If we minimally couple the vector potential to the momentum, we first find the dominant term \({\sigma }_{zz}^{0}\propto 1/| B| \), as discussed above.
In addition to minimal coupling, a magnetic field can couple to the electron dispersion directly, if its Bloch states have an orbital magnetic moment M(k). In this case, we can write
Note that M(k) is a pseudovector. If TRS is present, M(k) is an odd function of k. If in addition inversion symmetry is present, we find M(k) ≡ 0. This should be the case above the CDW transition temperature. In the CDW phase, by contrast, the various broken symmetries enable M(k) to be non-vanishing. For concreteness, we will now only discuss the case of broken x mirror symmetry, which is sufficient to explain the experimentally observed response. In this case, we find to lowest order in k that Mx(k) ∝ kz. If, further, this symmetry breaking is due to an ordered phase with order parameter ΔCDW, we can expand in both k and ΔCDW and write \({M}_{x}({\bf{k}})\approx \widetilde{M}{\Delta }^{{\rm{CDW}}}{k}_{z}\) with \(\widetilde{M}\) a model-dependent constant.
We can now use eqns (8) and (9) to calculate the velocity in the z direction,
(More generally, Mx(k) will be an odd function of kz, such that the additional contribution to the velocity will be even.) Finally, we find for the conductivity in the z direction (dropping, for simplicity, the subscripts zz)
up to the order of Bx(ΔCDW)2. Here we have used the stationary Fermi distribution to calculate the current carried by the system. We thus find an additional contribution to the conductivity Δσ ∝ BxIz, which will result in a second-harmonic signal in an a.c. electric field applied in the z direction.
To further support the above arguments for the case of CsV3Sb5, we have performed a tight-binding calculation, which shows, in the chiral CDW phase, that: (1) the Fermi-surface structure does indeed become more structured with sharp corners, and (2) a finite orbital magnetic moment Mx arises, see Extended Data Fig. 9.
Note that, experimentally, we find that a small magnetic field in the z direction can change the sign of the observed signal. This implies that a magnetic field Bz couples linearly to the order parameter ΔCDW, which in turn implies that the order breaks TRS in addition to the mirrors Mx and My. This is in agreement with the experimental findings in ref. 28. In terms of a simple Landau theory,
with α < 0, β > 0 and γ ≪ ∣α∣, β, the CDW order parameter is \({\Delta }^{{\rm{C}}{\rm{D}}{\rm{W}}}\approx {\rm{s}}{\rm{i}}{\rm{g}}{\rm{n}}({B}_{z})\sqrt{-\alpha /\beta }={\rm{s}}{\rm{i}}{\rm{g}}{\rm{n}}(\theta ){\Delta }_{0}\), with \({B}_{z}=| {\bf{B}}| \sin \theta \), implying its sign change with Bz.
In summary, for the slope of the chiral conductivity, we find
For small angles θ off the basal plane, this yields a step function in good qualitative agreement with the experimentally extracted form for small angles θ. Moreover, combining the angular dependence of both the theoretically predicted chiral conductivity and the experimentally measured magnetoresistance, we also derived the second-harmonic voltage V2ω as a function of angle (Extended Data Fig. 10), which is also consistent with the experimental results.
Finally, if we want to compare the conductivity calculated above to the experiment and the standard eMChA literature, we need to express the conductivity in eqn (12) as a resistance. Namely, one usually writes R(B,I) = R + ΔR/2, where in general R can depend on B, and in particular here we have R ≈ ∣B∣. We thus find
This yields Δσ ≈ −ΔR/2R2 and in turn, we expect
By applying a low-frequency a.c. current Iω = I0sin(ωt), the generated electric voltage can be expressed as:
here VDC stands for the d.c. background voltage. This yields:
which also suggests:
exactly in line with our experimental data.
Data availability
Data that support the findings of this study are deposited to Zenodo with the access link: https://doi.org/10.5281/zenodo.6787797.
References
Rikken, G. L. J. A. & Avarvari, N. Strong electrical magnetochiral anisotropy in tellurium. Phys. Rev. B 99, 245153 (2019).
Rikken, G. L. J. A., Fölling, J. & Wyder, P. Electrical magnetochiral anisotropy. Phys. Rev. Lett. 87, 236602 (2001).
Wei, J. et al. Magnetic-field asymmetry of nonlinear transport in carbon nanotubes. Phys. Rev. Lett. 95, 256601 (2005).
Pop, F., Auban-Senzier, P., Canadell, E., Rikken, G. L. J. A. & Avarvari, N. Electrical magnetochiral anisotropy in a bulk chiral molecular conductor. Nat. Commun. 5, 3757 (2014).
Aoki, R., Kousaka, Y. & Togawa, Y. Anomalous nonreciprocal electrical transport on chiral magnetic order. Phys. Rev. Lett. 122, 057206 (2019).
Yokouchi, T. et al. Electrical magnetochiral effect induced by chiral spin fluctuations. Nat. Commun. 8, 866 (2017).
Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).
Mielke, C. et al. Time-reversal symmetry-breaking charge order in a kagome superconductor. Nature 602, 245–250 (2022).
Yu, L. et al. Evidence of a hidden flux phase in the topological kagome metal CsV3Sb5. Preprint at https://doi.org/10.48550/arXiv.2107.10714 (2021).
Nie, L. et al. Charge-density-wave-driven electronic nematicity in a kagome superconductor. Nature 604, 59–64 (2022).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Lv, B. Q., Qian, T. & Ding, H. Experimental perspective on three-dimensional topological semimetals. Rev. Mod. Phys. 93, 025002 (2021).
Brandt, J. R., Salerno, F. & Fuchter, M. J. The added value of small-molecule chirality in technological applications. Nat. Rev. Chem. 1, 0045 (2017).
Yang, S.-H., Naaman, R., Paltiel, Y. & Parkin, S. S. P. Chiral spintronics. Nat. Rev. Phys. 3, 328–343 (2021).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Atzori, M., Train, C., Hillard, E. A., Avarvari, N. & Rikken, G. L. Magneto-chiral anisotropy: from fundamentals to perspectives. Chirality 33, 844–857 (2021).
Liang, Z. et al. Three-dimensional charge density wave and surface-dependent vortex-core states in a kagome superconductor CsV3Sb5. Phys. Rev. X 11, 031026 (2021).
Xiang, Y. et al. Twofold symmetry of c-axis resistivity in topological kagome superconductor CsV3Sb5 with in-plane rotating magnetic field. Nat. Commun. 12, 6727 (2021).
Kang, M. et al. Twofold van Hove singularity and origin of charge order in topological kagome superconductor CsV3Sb5. Nat. Phys. 18, 301–308 (2022).
Denner, M. M., Thomale, R. & Neupert, T. Analysis of charge order in the kagome metal AV3Sb5 (A = K, Rb, Cs). Phys. Rev. Lett. 127, 217601 (2021).
Ortiz, B. R. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mater. 3, 094407 (2019).
Ortiz, B. R. et al. CsV3Sb5: A \({{\mathbb{Z}}}_{2}\) topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).
Yu, F. et al. Concurrence of anomalous Hall effect and charge density wave in a superconducting topological kagome metal. Phys. Rev. B 104, L041103 (2021).
Mu, C. et al. S-wave superconductivity in kagome metal CsV3Sb5 revealed by 121/123Sb NQR and 51V NMR measurements. Chin. Phys. Lett. 38, 077402 (2021).
Neupert, T., Denner, M. M., Yin, J.-X., Thomale, R. & Hasan, M. Z. Charge order and superconductivity in kagome materials. Nat. Phys. 18, 137–143 (2022).
Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353–1357 (2021).
Luo, J. et al. Possible star-of-David pattern charge density wave with additional modulation in the kagome superconductor CsV3Sb5. npj Quantum Mater. 7, 30 (2022).
Stahl, Q. et al. Temperature-driven reorganization of electronic order in CsV3Sb5. Phys. Rev. B 105, 195136 (2022).
Huang, X. et al. Mixed dimensional transport in CsV3Sb5 single crystals. Preprint at https://doi.org/10.48550/arXiv.2201.07780 (2022).
Grüner, G. The dynamics of charge-density waves. Rev. Mod. Phys. 60, 1129 (1988).
Li, H. et al. Rotation symmetry breaking in the normal state of a kagome superconductor KV3Sb5. Nat. Phys. 18, 137–143 (2022).
Chen, D. et al. Anomalous thermoelectric effects and quantum oscillations in the kagome metal CsV3Sb5. Phys. Rev. B 105, L201109 (2021).
Ishioka, J. et al. Chiral charge-density waves. Phys. Rev. Lett. 105, 176401 (2010).
Feng, X., Jiang, K., Wang, Z. & Hu, J. Chiral flux phase in the kagome superconductor AV3Sb5. Sci. Bull. 66, 1384–1388 (2021).
Lin, Y.-P. & Nandkishore, R. M. Complex charge density waves at Van Hove singularity on hexagonal lattices: Haldane-model phase diagram and potential realization in the kagome metals AV3Sb5 (A = K, Rb, Cs). Phys. Rev. B 104, 045122 (2021).
Feng, Y. et al. Linear magnetoresistance in the low-field limit in density-wave materials. Proc. Natl Acad. Sci. USA 116, 11201–11206 (2019).
Zhang, C.-L. et al. Signatures of the Adler–Bell–Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Commun. 7, 10735 (2016).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Mat. 29, 465901 (2017).
Takatsu, H. et al. Extremely large magnetoresistance in the nonmagnetic metal PdCoO2. Phys. Rev. Lett. 111, 056601 (2013).
Lu, L., Yi, W. & Zhang, D. L. 3ω method for specific heat and thermal conductivity measurements. Rev. Sci. Instrum. 72, 2996–3003 (2001).
Huang, X. W. et al. Non-linear Shubnikov–de Haas oscillations in the self-heating regime. Phys. Rev. Lett. 111, 056601 (2013).
Abrikosov, A. A. Quantum linear magnetoresistance. Europhys. Lett. 49, 789–793 (2000).
Acknowledgements
This work was funded by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (MiTopMat, grant agreement no. 715730, and PARATOP, grant agreement no. 757867). This project received funding by the Swiss National Science Foundation (grant no. PP00P2_176789). M.G.V., I.E. and M.G.-A. acknowledge the Spanish Ministerio de Ciencia e Innovacion (grant PID2019-109905GB-C21). M.G.V., C.F. and T.N. acknowledge support from FOR 5249 (QUAST) lead by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation). This work has been supported in part by Basque Government grant IT979-16. This work was also supported by the European Research Council Advanced Grant (no. 742068) ‘TOPMAT’, the Deutsche Forschungsgemeinschaft (Project-ID no. 247310070) ‘SFB 1143’ and the DFG through the Würzburg–Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter ct.qmat (EXC 2147, Project-ID no. 390858490).
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
Crystals were synthesized and characterized by D.C. and C.F. The experiment design, FIB microstructuring, the magnetotransport measurements and the second-harmonic voltage measurements were performed by C.G., C.P., S.K., X.H. and P.J.W.M. M.H.F. and T.N. developed and applied the general theoretical framework, and the analysis of experimental results has been done by C.G., C.P. and P.J.W.M. Band structures were calculated by M.G.-A., I.E. and M.G.V. All authors were involved in writing the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review information
Peer review information
Nature thanks Hai-Hu Wen, Lan Wang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Basic properties of CsV3Sb5.
a, Crystal structure of CsV3Sb5. b, XRD pattern of the (001) facet of a CsV3Sb5 crystal. c, Band structure of CsV3Sb5 calculated by density functional theory (DFT) using the Quantum Espresso package (QE)41. d, Field dependence of magnetoresistivity and Hall resistivity measured at T = 5 K. A large quasi-linear magnetoresistance is observed up to B = 18 T. In comparison, the Hall resistivity is almost negligible.
Extended Data Fig. 2 Angular dependence of magnetoresistivity and eMChA.
a, Angle-dependent magnetoresistivity of CsV3Sb5 measured with B = 18 T at various temperatures. A strong spike can be observed around θ = 0 deg which becomes broader with increasing temperatures. b, Correspondingly, V2ω also gets pronounced within the same angle range. c, The V2ω depends linearly on the square of c-axis resistivity, which demonstrates the direct connection between magneto-resistivity and eMChA.
Extended Data Fig. 3 Current dependence of first and second harmonic voltage.
a, b, Current-dependence of both Vω and V2ω. As expected Vω depends linearly on current while V2ω displays a quadratic current dependence. c, Summary ofthe relation between V2ω and Vω, which shows a parabolic dependence.
Extended Data Fig. 4 Influence of Joule heating effect.
Current-dependence of V2ω measured at B = 18 T and T = 2 K with varying levels of helium exchange gas pressure in the cryostat. The curves differ only at currents above 0.12 mA, suggesting that the heat generation and accumulation at lower currents is not a dominant factor. eMChA was measured at lower values of 0.1 mA.
Extended Data Fig. 5 Reproducibility of eMChA with two different devices.
a, Scanning electron microscope (SEM) images of devices S1 and S2. b, Temperature-dependent resistivity of S1 and S2 from 300 K to 1.6 K. c, Angle-dependent second harmonic voltage measured at B = 18 T and T = 2 K.
Extended Data Fig. 6 Illustration of device configuration for both S1 and S2.
While S1 is completely suspended by the membrane springs, S2 is attached to the Si-substrate frame on one side and membrane springs on the other side.
Extended Data Fig. 7 Strain effect on eMChA.
a, SEM image of device S4. The sample is attached to the sapphire substrate via a glue droplet. The thin beam along the c-axis allows us to measure the electric response with both current and tensile strain applied along the c-axis. b, Temperature dependence of resistivity for S1 and S4. The CDW transition is enhanced to a higher temperature with tensile strain along the c-axis (S4), while Tc is reduced to lower temperature. c, Angular spectrum of second harmonic voltage (V2ω). Clearly V2ω is completely suppressed with tensile strain along c-axis.
Extended Data Fig. 8 Field-symmetry analysis of second harmonic voltage.
a, Temperature dependence of V2ω measured at B = ± 18 T respectively. b, Temperature-dependent field-symmetric and asymmetric part of V2ω.
Extended Data Fig. 9 Tight-binding model on the stacked triangular lattice with 2 × 2 × 2 chiral CDW order.
a, The unit cell of the model consists of 8 lattice sites (black) on two layers, each harbouring a single electronic orbital. The model is defined by the hoppings as indicated, where ω = ei2π/3 (all complex hoppings are oriented to the right). All dashed lines are associated with real hopping amplitude tz. We choose numerical values t = 1, tz = 0.2, Δ = 0.05. b, Fermi surface of the model for chemical potential μ = 2.4 (black lines) and orbital magnetic moment component Mx of the states closest to the Fermi level. We observe that Mx is not only finite, but also large for states on the Fermi surface. c, Band structure along kz for a particular choice of kx and ky, coloured by the orbital magnetic moment component Mx, demonstrating that Mx is an odd function of kz as required for the measured nonlinear response to be nonvanishing.
Extended Data Fig. 10 Comparison between experimental results and theoretical prediction.
a, Experimentally measured and b, theoretically predicted angular dependence of second harmonic voltage V2ω with B = 18 T and T = 2 K.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Guo, C., Putzke, C., Konyzheva, S. et al. Switchable chiral transport in charge-ordered kagome metal CsV3Sb5. Nature 611, 461–466 (2022). https://doi.org/10.1038/s41586-022-05127-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-05127-9
This article is cited by
-
Distinct switching of chiral transport in the kagome metals KV3Sb5 and CsV3Sb5
npj Quantum Materials (2024)
-
Signatures of a surface spin–orbital chiral metal
Nature (2024)
-
Correlated order at the tipping point in the kagome metal CsV3Sb5
Nature Physics (2024)
-
Spin Berry curvature-enhanced orbital Zeeman effect in a kagome metal
Nature Physics (2024)
-
Evidence for an odd-parity nematic phase above the charge-density-wave transition in a kagome metal
Nature Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.