Abstract
Reliable sensory discrimination must arise from high-fidelity neural representations and communication between brain areas. However, how neocortical sensory processing overcomes the substantial variability of neuronal sensory responses remains undetermined1,2,3,4,5,6. Here we imaged neuronal activity in eight neocortical areas concurrently and over five days in mice performing a visual discrimination task, yielding longitudinal recordings of more than 21,000 neurons. Analyses revealed a sequence of events across the neocortex starting from a resting state, to early stages of perception, and through the formation of a task response. At rest, the neocortex had one pattern of functional connections, identified through sets of areas that shared activity cofluctuations7,8. Within about 200 ms after the onset of the sensory stimulus, such connections rearranged, with different areas sharing cofluctuations and task-related information. During this short-lived state (approximately 300 ms duration), both inter-area sensory data transmission and the redundancy of sensory encoding peaked, reflecting a transient increase in correlated fluctuations among task-related neurons. By around 0.5 s after stimulus onset, the visual representation reached a more stable form, the structure of which was robust to the prominent, day-to-day variations in the responses of individual cells. About 1 s into stimulus presentation, a global fluctuation mode conveyed the upcoming response of the mouse to every area examined and was orthogonal to modes carrying sensory data. Overall, the neocortex supports sensory performance through brief elevations in sensory coding redundancy near the start of perception, neural population codes that are robust to cellular variability, and widespread inter-area fluctuation modes that transmit sensory data and task responses in non-interfering channels.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data supporting the findings of this study are available from the corresponding authors on reasonable request.
Code availability
We used open source software routines for image registration55 (http://bigwww.epfl.ch/thevenaz/turboreg/) and PLS analysis (https://www.mathworks.com/matlabcentral/fileexchange/18760-partial-least-squares-and-discriminant-analysis). Software code for extracting individual neurons and their calcium activity traces from calcium videos by using principal component and then independent component analyses56 is available online for free (https://www.mathworks.com/matlabcentral/fileexchange/25405-emukamel-cellsort), although, for convenience, we used a commercial version of these routines (Mosaic software, v.0.99.17, Inscopix). We used MATLAB (v.2019a) to write all other analytical routines. The primary software code used to support the findings of the study is available at Zenodo (https://doi.org/10.5281/zenodo.6314932).
References
Faisal, A. A., Selen, L. P. & Wolpert, D. M. Noise in the nervous system. Nat. Rev. Neurosci. 9, 292–303 (2008).
Lutcke, H., Margolis, D. J. & Helmchen, F. Steady or changing? Long-term monitoring of neuronal population activity. Trends Neurosci. 36, 375–384 (2013).
Rumyantsev, O. I. et al. Fundamental bounds on the fidelity of sensory cortical coding. Nature 580, 100–105 (2020).
Stein, R. B., Gossen, E. R. & Jones, K. E. Neuronal variability: noise or part of the signal? Nat. Rev. Neurosci. 6, 389–397 (2005).
Zohary, E., Shadlen, M. N. & Newsome, W. T. Correlated neuronal discharge rate and its implications for psychophysical performance. Nature 370, 140–143 (1994).
Driscoll, L. N., Pettit, N. L., Minderer, M., Chettih, S. N. & Harvey, C. D. Dynamic reorganization of neuronal activity patterns in parietal cortex. Cell 170, 986–999 (2017).
Greicius, M. D., Supekar, K., Menon, V. & Dougherty, R. F. Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb. Cortex 19, 72–78 (2009).
Rosenberg, M. D. et al. A neuromarker of sustained attention from whole-brain functional connectivity. Nat. Neurosci. 19, 165–171 (2016).
Montijn, J. S., Meijer, G. T., Lansink, C. S. & Pennartz, C. M. Population-level neural codes are robust to single-neuron variability from a multidimensional coding perspective. Cell Rep. 16, 2486–2498 (2016).
Semedo, J. D., Zandvakili, A., Machens, C. K., Byron, M. Y. & Kohn, A. Cortical areas interact through a communication subspace. Neuron 102, 249–259 (2019).
Stringer, C. et al. Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255 (2019).
Abbott, L. F. & Dayan, P. The effect of correlated variability on the accuracy of a population code. Neural Comput. 11, 91–101 (1999).
Averbeck, B. B. & Lee, D. Effects of noise correlations on information encoding and decoding. J. Neurophysiol. 95, 3633–3644 (2006).
Moreno-Bote, R. et al. Information-limiting correlations. Nat. Neurosci. 17, 1410–1417 (2014).
Carrillo-Reid, L., Han, S., Yang, W., Akrouh, A. & Yuste, R. Controlling visually guided behavior by holographic recalling of cortical ensembles. Cell 178, 447–457 (2019).
Graf, A. B., Kohn, A., Jazayeri, M. & Movshon, J. A. Decoding the activity of neuronal populations in macaque primary visual cortex. Nat. Neurosci. 14, 239–245 (2011).
Ziv, Y. et al. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266 (2013).
Xia, J., Marks, T. D., Goard, M. J. & Wessel, R. Stable representation of a naturalistic movie emerges from episodic activity with gain variability. Nat. Commun. 12, 5170 (2021).
Gonzalez, W. G., Zhang, H., Harutyunyan, A. & Lois, C. Persistence of neuronal representations through time and damage in the hippocampus. Science 365, 821–825 (2019).
Deitch, D., Rubin, A. & Ziv, Y. Representational drift in the mouse visual cortex. Curr. Biol. 31, 4327–4339 (2021).
Sridharan, D., Levitin, D. J. & Menon, V. A critical role for the right fronto-insular cortex in switching between central-executive and default-mode networks. Proc. Natl Acad. Sci. USA 105, 12569–12574 (2008).
Allen, W. E. et al. Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science 364, 253 (2019).
Musall, S., Kaufman, M. T., Juavinett, A. L., Gluf, S. & Churchland, A. K. Single-trial neural dynamics are dominated by richly varied movements. Nat. Neurosci. 22, 1677–1686 (2019).
Niell, C. M. & Stryker, M. P. Modulation of visual responses by behavioral state in mouse visual cortex. Neuron 65, 472–479 (2010).
Montani, F., Kohn, A., Smith, M. A. & Schultz, S. R. The role of correlations in direction and contrast coding in the primary visual cortex. J. Neurosci. 27, 2338–2348 (2007).
Goard, M. J., Pho, G. N., Woodson, J. & Sur, M. Distinct roles of visual, parietal, and frontal motor cortices in memory-guided sensorimotor decisions. eLife 5, e13764 (2016).
Poort, J. et al. Learning enhances sensory and multiple non-sensory representations in primary visual cortex. Neuron 86, 1478–1490 (2015).
Britten, K. H., Shadlen, M. N., Newsome, W. T. & Movshon, J. A. The analysis of visual motion: a comparison of neuronal and psychophysical performance. J. Neurosci. 12, 4745–4765 (1992).
Kanitscheider, I., Coen-Cagli, R. & Pouget, A. Origin of information-limiting noise correlations. Proc. Natl Acad. Sci. USA 112, E6973–E6982 (2015).
Bullmore, E. & Sporns, O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 10, 186–198 (2009).
Yu, Y., Stirman, J. N., Dorsett, C. R. & Smith, S. L. Mesoscale correlation structure with single cell resolution during visual coding. Preprint at bioRxiv https://doi.org/10.1101/469114 (2018).
Gregoriou, G. G., Gotts, S. J. & Desimone, R. Cell-type-specific synchronization of neural activity in FEF with V4 during attention. Neuron 73, 581–594 (2012).
Gregoriou, G. G., Gotts, S. J., Zhou, H. & Desimone, R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science 324, 1207–1210 (2009).
Ruff, D. A. & Cohen, M. R. Attention increases spike count correlations between visual cortical areas. J. Neurosci. 36, 7523–7534 (2016).
van Kempen, J. et al. Top-down coordination of local cortical state during selective attention. Neuron 109, 894–904 (2021).
Chen, J. L., Voigt, F. F., Javadzadeh, M., Krueppel, R. & Helmchen, F. Long-range population dynamics of anatomically defined neocortical networks. eLife 5, e14679 (2016).
Doiron, B., Litwin-Kumar, A., Rosenbaum, R., Ocker, G. K. & Josic, K. The mechanics of state-dependent neural correlations. Nat. Neurosci. 19, 383–393 (2016).
Churchland, M. M. et al. Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat. Neurosci. 13, 369–378 (2010).
Wagner, M. J. et al. Shared cortex-cerebellum dynamics in the execution and learning of a motor task. Cell 177, 669–682 (2019).
Steinmetz, N. A., Zatka-Haas, P., Carandini, M. & Harris, K. D. Distributed coding of choice, action and engagement across the mouse brain. Nature 576, 266–273 (2019).
Britten, K. H., Newsome, W. T., Shadlen, M. N., Celebrini, S. & Movshon, J. A. A relationship between behavioral choice and the visual responses of neurons in macaque MT. Vis. Neurosci. 13, 87–100 (1996).
Keller, A. J., Roth, M. M. & Scanziani, M. Feedback generates a second receptive field in neurons of the visual cortex. Nature 582, 545–549 (2020).
Bondy, A. G., Haefner, R. M. & Cumming, B. G. Feedback determines the structure of correlated variability in primary visual cortex. Nat. Neurosci. 21, 598–606 (2018).
Zipser, K., Lamme, V. A. & Schiller, P. H. Contextual modulation in primary visual cortex. J. Neurosci. 16, 7376–7389 (1996).
Mashour, G. A., Roelfsema, P., Changeux, J. P. & Dehaene, S. Conscious processing and the global neuronal workspace hypothesis. Neuron 105, 776–798 (2020).
Cohen, M. X. & Ranganath, C. Reinforcement learning signals predict future decisions. J. Neurosci. 27, 371–378 (2007).
Bassett, D. S. & Bullmore, E. Small-world brain networks. Neuroscientist 12, 512–523 (2006).
Oh, S. W. et al. A mesoscale connectome of the mouse brain. Nature 508, 207–214 (2014).
Garrett, M. E., Nauhaus, I., Marshel, J. H. & Callaway, E. M. Topography and areal organization of mouse visual cortex. J. Neurosci. 34, 12587–12600 (2014).
Kalatsky, V. A. & Stryker, M. P. New paradigm for optical imaging: temporally encoded maps of intrinsic signal. Neuron 38, 529–545 (2003).
Marshel, J. H., Garrett, M. E., Nauhaus, I. & Callaway, E. M. Functional specialization of seven mouse visual cortical areas. Neuron 72, 1040–1054 (2011).
Zhuang, J. et al. An extended retinotopic map of mouse cortex. eLife 6, e18372 (2017).
Lecoq, J. et al. Visualizing mammalian brain area interactions by dual-axis two-photon calcium imaging. Nat. Neurosci. 17, 1825–1829 (2014).
Lein, E. S. et al. Genome-wide atlas of gene expression in the adult mouse brain. Nature 445, 168–176 (2007).
Thevenaz, P., Ruttimann, U. E. & Unser, M. A pyramid approach to subpixel registration based on intensity. IEEE Trans. Image Process. 7, 27–41 (1998).
Mukamel, E. A., Nimmerjahn, A. & Schnitzer, M. J. Automated analysis of cellular signals from large-scale calcium imaging data. Neuron 63, 747–760 (2009).
Kanitscheider, I., Coen-Cagli, R., Kohn, A. & Pouget, A. Measuring Fisher information accurately in correlated neural populations. PLoS Comput. Biol. 11, e1004218 (2015).
Barker, M. & Rayens, W. Partial least squares for discrimination. J. Chemometr. 17, 166–173 (2003).
Wold, H. in Multivariate Analysis (ed. Krishnajah, P. R.) 391–420 (Academic, 1966).
Kohn, A. & Smith, M. A. Stimulus dependence of neuronal correlation in primary visual cortex of the macaque. J. Neurosci. 25, 3661–3673 (2005).
Hotelling, H. in Breakthroughs in Statistics Vol. 2 (eds S. Kotz & N.L. Johnson) 162–190 (Springer, 1992).
Witten, D. M. & Tibshirani, R. J. Extensions of sparse canonical correlation analysis with applications to genomic data. Stat. Appl. Genet. Mol. Biol. 8, Article28 (2009).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’networks. Nature 393, 440–442 (1998).
Honey, C. J., Kotter, R., Breakspear, M. & Sporns, O. Network structure of cerebral cortex shapes functional connectivity on multiple time scales. Proc. Natl Acad. Sci. USA 104, 10240–10245 (2007).
Lu, J., Yu, X., Chen, G. & Cheng, D. Characterizing the synchronizability of small-world dynamical networks. IEEE Trans. Circ. Syst. I 51, 787–796 (2004).
Acknowledgements
We thank B. Ahanonu, A. Christensen, H. Kim, T. Rogerson, A. Shai and A. Tsao for conversations, and H. Zeng for providing transgenic mice. We acknowledge research support from HHMI (to M.J.S.); the Stanford CNC Program (to M.J.S.); DARPA (to M.J.S.); NIH BRAIN Initiative grant 1UF1NS107610-01 (to M.J.S.); the NSF NeuroNex Program (to M.J.S.); an NSF CAREER Award (to S.G.); the Burroughs-Wellcome (to S.G.), McKnight (to S.G.), James S. McDonnell (to S.G.) and Simons (to S.G. and M.J.S.) foundations; and a Stanford Graduate Fellowship (to O.R.).
Author information
Authors and Affiliations
Contributions
S.E., J.A.L., S.G. and M.J.S. designed the study. S.E., J. Lecoq, O.R., T.T., C.I. and M.J.S. designed the experiments. J. Lecoq, O.R. and M.J.S. designed the microscope. J. Lecoq, C.I., S.E. and T.T. trained mice and acquired the data. S.E., S.G. and M.J.S. designed the analyses. S.E. analysed the data and performed the network simulations. S.G. did the theoretical and computational analyses of the Supplementary Information. Y.Z. and J. Lecoq. performed mouse surgeries. Y.Z. and J. Li performed histological analyses and husbandry. S.E., S.G. and M.J.S. wrote the paper. All of the authors edited the paper. S.G. and M.J.S supervised the research.
Corresponding authors
Ethics declarations
Competing interests
M.J.S. is a scientific co-founder of Inscopix, which produces the Mosaic software used to identify individual neurons in the Ca2+ videos. J. Lecoq. is also an Inscopix stockholder.
Peer review
Peer review information
Nature thanks Tatiana Engel and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Long-term imaging and computational analysis of neural Ca2+ dynamics across multiple cortical areas during a visual discrimination task.
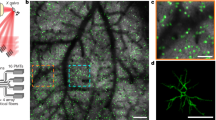
(a) Schematic of the algorithmic pipeline used for video preprocessing and cell extraction, as implemented using cluster computing. Pre-processing (steps shown in green): For each movie of Ca2+ activity, we performed an image registration across all frames of the movie to correct for small displacements of the brain. We removed background noise and neuropil Ca2+ activity by applying a spatial Gaussian high-pass filter (σ = 80 μm) and computed a movie of the relative changes in fluorescence (ΔF(t)/F0). We then aligned and concatenated all the ΔF(t)/F0 movies for each individual mouse, across all imaging sessions. Cell extraction (steps shown in yellow): We divided each concatenated movie into 16 spatial tiles and then extracted individual cells within each tile by successively applying principal component and independent component analyses (PCA/ICA algorithm)56 to all tiles in parallel using the Stanford Sherlock computing cluster (using up to 320 cores and ~2 TB of memory for each concatenated movie). Ca2+ event detection (steps shown in cyan): We converted the ΔF(t)/F0 traces for each neuron to traces expressing the time-dependent fluorescence changes as a z-score, z(t), relative to the s.d. of the baseline fluctuations in each cell’s fluorescence trace (computed separately for each imaging session). We detected Ca2+ events by identifying Ca2+ transients that attained a peak fluorescence value of z(t) ≥ 4 s.d., and we assigned the cell as being ‘active’ within the interval between the initial threshold crossing and the time at which the Ca2+ event attained its peak fluorescence (Methods). (b) Left: A maximum projection image over an entire concatenated set of Ca2+ movies from an example mouse. Red lines mark the 4 × 4 set of tiles that we processed in parallel during cell extraction. Scale bar: 1 mm. Middle: Magnified view of the area enclosed in orange in the left panel. Scale bar: 0.1 mm. Right: Z-scored traces (coloured traces) of fluorescence Ca2+ activity for 10 example neurons in the middle panel marked with colour-corresponding boundaries. Raster traces show the binarized patterns of activity for each cell. (c) Most detected cells were active in all recording sessions, as illustrated via a map, computed for one example mouse, in which each detected cell is marked with a colour-code indicating the number of days in which it was detected as active (Methods). Scale bar: 1 mm. (d) Histograms of the number of days that each cell was detected as active for 6 different mice. Error bars are s.d. estimated as counting errors. (e) Vertical and horizontal retinotopic maps of visual cortex in an example mouse (Methods). After identifying borders of area V1 determined by retinotopic mapping studies in each mouse, we aligned these borders with those in the Allen Brain Observatory map of the mouse cortex and thereby inferred the locations of other brain areas. (f) Histogram of the mean Ca2+ event rate for each of 21,570 cortical neurons (N = 6 mice). Error bars are s.d. estimated as counting errors. (g) Mean probability of licking within individual time bins (0.1 s duration) over the time course of a trial, averaged over all trials and trained mice, for Go (green) and No-Go (red) trials. Shaded areas denote s.e.m. over N = 6 mice. After mice learned to discriminate between Go and No-Go visual stimuli, we trained them to withhold licking behaviour during the stimulus presentation, [0 s, 2 s], and delay, [2 s, 2.5 s], intervals and to respond only during the response interval, [2.5 s, 5.5 s] (Fig. 1 and Methods). Trained mice occasionally licked before the response interval; we discarded these trials from our analyses to allow inferences regarding stimulus encoding, decision-making, and motor preparation in the absence of overt licking responses. (h) The mean behavioral performance of all mice on Go (cyan) and No-Go (grey) trials in which the mouse did (right) or did not exhibit locomotor behaviour (left) (Methods). Individual data points denote values from individual mice. (i, j) For every individual cell (blue data points), the plots show the mean signal-to-noise ratio (SNR) of Ca2+ activity, i, or the mean occurrence rate of Ca2+ transient events per time bin (0.1 s duration), j, in the first half of each imaging session versus that in the second half of the same session. From linear regression, the mean SNR and Ca2+ event rate in the second half of each session were 96 ± 2 % (N = 6 mice) and 99 ± 3 % (N = 6 mice), respectively, of their values in the first half. (k) A box and whisker plot of the Ca2+ event rate across all cells imaged for 5 days in each mouse (N = 2236-5292 cells). Horizontal lines indicate median values across all cells, boxes cover the second and third quartiles, and whiskers extend to 1.5 times the interquartile distance. Dots show median values for individual mice.
Extended Data Fig. 2 Cortical neurons exhibit variable coding properties across timescales from minutes to days.
(a) Maps for two example mice, showing how mean lateral displacements in cells’ centroid positions across multiple imaging sessions depended on their locations in the field of view. Across most of the field of view, mean displacements were <1 pixel, corresponding to <4 μm. To determine these displacements, we first computed the maximum projection image (MPI) of the Ca2+ video from each session. Using the MPI from the first session as a reference, we computationally aligned it to the MPI from each of the other sessions. We then computed the spatial cross-correlation function between patches of the MPI containing ≥10 cells from the first session (patch size: 256 μm × 256 μm) and MPIs from each of the other sessions. For each session other than the first, we determined the displacement of a patch to be the argument of the cross-correlation function that yielded its maximum value. We averaged these displacements across all sessions after the first. By examining all possible MPI patches (spaced 64 μm apart) in this way, we created the maps shown. Scale bars: 1 mm. (b) Two-dimensional probability distribution of cells’ daily lateral displacements from their mean position, averaged across all days and imaged neurons (21,570 cells) from N = 6 mice (Methods). About 50% of the time, cells had a displacement of zero pixels from their mean position; 98.5% of the time these displacements were ≤1 pixel (4 μm). (c) Cumulative distribution of cells’ mean displacements (averaged over all sessions) from their mean positions across the entire experiment. Red dashed line indicates that 95.4% of cells had a mean displacement of ≤5 μm. (d) Cumulative distribution of the lateral separations between nearest neighbour cell pairs. Red dashed line indicates that only 2% of nearest neighbour cell pairs were within 5 μm of each other. (e) Among 18,528 cells with significant d’ values on one or more sessions for encoding the trial-type in the stimulus period (P < 0.01; permutation test; N = 94–354 trials), 41% of these had significant d’ values in only one half-session, split nearly evenly between the first (21%) and second (20%) half-sessions. Whereas in trial-shuffled data, only 10% of the cells had this variable coding, a highly significant difference from the real data (P<0.001) indicating that trial-shuffling diluted the temporal concentration of trials in which cells had coding responses. In real data, 91% of the 18,528 cells retained significant coding in one or both halves of the full sessions in which they displayed significant coding (P<0.01; permutation test; 40–175 trials). But in trial-shuffled data, only 51% of the cells retained this coding in one or both half-sessions, a highly significant difference from real data (***P<0.001; permutation test; 94–354 trials), again showing that in real data cells had temporally concentrated coding epochs far more than expected by chance. All s.d. values on the above percentages of cells were estimated as counting errors and were 0.1–0.4%. (f) Some neurons had coding properties that varied across days. For 4 example cells (from areas PPC, MV, V1 and PPC, from top to bottom), shown are traces of the neuron’s fluorescence intensity (z-scored values of ΔF/F0) as a function of time across 5 imaging sessions. Vertical dashed lines mark transitions between successive sessions. Insets show maximum projection images of the example neurons from each session. Values of d’ denote the fidelity with which one can distinguish the two visual stimuli based on the binarized event train of the cell’s Ca2+ activity (Methods). In f and g, values of d’ coloured red are those for which the stimuli cannot be significantly distinguished, as determined using a permutation test over the set of stimulus trials and requiring P<0.01 for significance. (g) Some cells had coding properties that varied within the 1-h sessions. Shown are fluorescence traces (z-scored values of ΔF/F0) for 4 cells (from areas LV, V1, MV and LV, from top to bottom) as a function of time across one session. We measured d’ values of single neurons for distinguishing the two visual stimuli during the first and second halves of each session based on their binarized Ca2+ event traces. Neurons that actively fired across the session exhibited variability in their visual coding, as did cells that were active during only a portion of the imaging session. Insets: Example Ca2+ event images show that the same cells were imaged in the first and second halves of each session. (h) Histograms showing the numbers of days that neurons from each area significantly encoded the visual stimulus-type (permutation test over the set of stimulus trials; requiring P<0.01 for significance), for all cells that did so in at least one session (solid bars) and for the subset of these cells with statistically significant levels of Ca2+ activity in every imaging session (hashed bars). (i) Map of neurons from an example mouse, with each cell’s colour denoting the number of days the cell significantly encoded the visual-stimulus type. Cells with different day-to-day reliabilities of stimulus-encoding were interspersed across the field of view. Scale bar: 1 mm. (j) Scatter plot in which, for every individual cell (blue data points), the d’ value for stimulus discrimination during the first half of each imaging session is plotted against the d’ value for the second half of the same session. (k) Scatter plot in which, for every cell (blue data points), the mean d’ value for stimulus discrimination (averaged over all sessions) is plotted against the range of d’ values determined for the same cell across all sessions. (l) Scatter plot in which, for every cell (blue data points), the mean difference between the d’ values for stimulus discrimination determined for the first and second halves of each session is plotted against the s.d. of the d’ values determined for the same cell across all sessions. Variability in d’ values within a session was highly correlated (r = 0.81) with variability across sessions, suggesting some neurons have greater intrinsic variability in the fidelity of stimulus encoding than others.
Extended Data Fig. 3 Neural ensemble representations of the visual stimuli were invariant over most of the stimulation period.
(a) Mean time-dependent occurrence rates of Ca2+ transient events per time bin (0.1 s duration) across different intervals of the trial-structure (demarcated by vertical lines) for 24 neurons from 8 cortical areas, averaged across 5 sessions in one mouse on Go (blue traces) and No-Go (black) trials. Shading: s.d. across 415 trials of each type. (b) For cells that responded significantly to one of the two stimuli (see Fig. 2c), shown are mean percentages of coding cells responding to the Go stimulus in each of 8 areas. The remainder of coding cells responded to the No-Go stimulus. Error bars: s.d. across N = 6 mice. (c) Procedure for training cross-validated instantaneous or consensus linear decoders. After constructing an unbiased dataset with equal numbers of Go and No-Go trials, we divided the set of trials into 3 equal portions, one for dimensionality reduction, another for decoder training, and the third for decoder testing. Using the first subset, a partial least squares (PLS) analysis identified a low-dimensional subspace of the neural ensemble activity that was informative for stimulus discrimination. Within this subspace, we used the second subset of trials to train a Fisher linear decoder (indicated by the vector Wdecoder). We used the third subset to test decoder performance. For training and testing datasets, we computed the fidelity, d’, with which the stimuli could be distinguished. To train decoders for identifying the mouse’s decision, we followed the same procedures, starting with equal numbers of correctly and incorrectly performed trials with a given stimulus. (d) We trained consensus decoders during the stimulus, delay, and response intervals of correctly performed trials. Plots show mean (d’)2 values for decoder training (blue) and testing (red) datasets, versus the number of PLS dimensions used. When constructing each decoder, we used the number of PLS dimensions that maximized (d’)2 for testing datasets. All plotted (d’)2 values are separately normalized for each mouse to the maximum (d’)2 determined with the testing data. On average, with >5 PLS dimensions decoders overfit the training data, yielding greater (d’)2 values than for testing data. For shuffled datasets, 1 or 2 PLS dimensions yielded maximal (d’)2 values (data not shown). Shading: s.d. across N = 6 mice. (e) We determined the similarity of the subspaces defined by the top 3 PLS dimensions for each mouse on different days (1–5) or for its across-day, common decoder (C) (Methods). We used the top 3 dimensions, since these contain most of the information (d). The matrices show mean similarity values for all pairs of subspaces, averaged over N = 6 mice, for real (left) and shuffled (right) datasets. For real datasets, PLS dimensions for common decoders were highly similar to those for single-day decoders. (f) Optimal linear decoders of stimulus-type retained a constant form across stimulus presentation. Plots show Pearson correlation coefficients, r, between all pairs of instantaneous decoders (constructed using all imaged neurons in each mouse), for each time bin. (g) Due to the stationarity of the optimal decoders across stimulus presentation, f, consensus and instantaneous decoders performed nearly equivalently. Plots show mean (d’)2 values for consensus decoders of stimulus-type versus those for instantaneous decoders, for correctly performed trials. Each datum shows testing results attained by applying each decoder-type to data from one time bin during stimulus presentation. In some mice, e.g. Mice 5 and 6, the consensus decoder achieved slightly superior performance, presumably due to its larger training dataset. (h) Similar results to those of f, computed for different areas and averaged over 6 mice. (i) Similar results to those of Fig. 3c, computed separately for different areas. (j) To measure the information captured by trial-type decoders about the stimulus (S) or mouse’s response (R) in the stimulus (left), delay (middle) or response (right) periods, we projected neural activity on all 4 trial-types (Hit, Miss, Correct Rejection, and False Alarm) onto the common trial-type decoders trained for each period using correctly performed trials. We then computed (d’)2 values using trials in which either the stimulus or response was held constant but the other varied. Information, (d’)2, about the stimulus did not vary significantly between Lick and No-Lick trials, so we averaged (d’)2 values across both stimuli in each plot’s left column. Response-coding was much stronger on Go trials (see k), so right columns only show (d’)2 values from Go trials. Each blue point shows data from one mouse (mean±s.d., N = 100 different subsets of trials, each with equal numbers of trials of the two types). Red points: averages across mice (mean±s.e.m., N = 6). During the stimulus period, common decoders nearly exclusively captured stimulus information, which was 691±315 times greater (mean±s.e.m.; N = 6 mice) than information captured about the mouse’s response. In the delay period, response information rose. During the response period, common decoders captured response information that was comparable or greater to information about the stimulus. (k) The mean Fisher information encoded by neural ensemble activity about the stimulus-type was independent of the mouse’s response (top), as (d’)2 values for consensus common stimulus decoders trained and tested on ‘No-Lick’ trials were indistinguishable to those for ‘Lick’ trials (P <0.7; Wilcoxon signed-rank test; N = 6 mice). On ‘Go’ but not ‘No-Go’ trials, the upcoming response could be predicted (P<0.01; permutation test; N = 40–754 trials) from neural activity during stimulus presentation (bottom). For each comparison, we constructed training datasets for the two decoders to have equal numbers of trials, 50% of each type. Blue-shaded points are from individual mice; error bars are s.d. (N = 100 different randomly chosen sets of trials. Red points are means; error bars are s.d. (N = 6 mice). (l) Control analysis for Fig. 3c. Across-day common consensus decoders performed equivalently to single-day consensus decoders when they were trained with equally sized datasets. Here we trained common decoders by sub-sampling trials from each session so the training dataset had the same of number of trials as that of the day with the smallest number of trials. We trained single-day decoders using this same number of trials.
Extended Data Fig. 4 Neural ensemble representations of the visual stimuli and the mouse’s response were widespread across neocortical areas.
(a) Plots analogous to Fig. 3f for individual mice. In all 6 mice, day-to-day changes in coding were correlated with within-day, trial-to-trial fluctuations (r = 0.85, 0.66, 0.79, 0.76, 0.83, 0.76 and P was between 5 × 10–14–5 × 10–29 for mice 1–6 for the real datasets, but 0.1 ≤ r ≤ 0.15 and 0.12 ≤ P ≤ 0.92 for trial-shuffled datasets). (b) We trained consensus common decoders to discriminate the visual stimuli based on neural activity either in individual cortical areas or across the visible cortical regions, during stimulus presentation on ‘No-Lick’ trials (trials when the mouse withheld licking responses) and Lick trials (on which the mouse made a licking response). Thus, decoders for ‘No-Lick’ trials discriminated ‘Correct Rejection’ from ‘Miss’ trials, and decoders for ‘Lick’ trials discriminated ‘Hit’ from ‘False Alarm’ trials. Both decoder types were trained on equally sized datasets, with equal numbers of trials of each type. We evaluated decoder performance across individual time bins and then plotted the maximum (d’)2 values attained for each mouse across all time bins during stimulus presentation (0.5–2 s after stimulus onset). (d’)2 values for stimulus decoding were independent of the mouse’s upcoming ‘Lick’ or ‘No-Lick’ response (P<0.7; Wilcoxon signed-rank test, N = 6 mice). Across b–g, grey and coloured symbols respectively denote (d’)2 values for individual mice and mean values averaged over N = 6 mice; note that y-axis scales vary substantially across the graphs. (c, d) Using the methods of b, we trained consensus common decoders to discriminate the visual stimuli using neural activity in different cortical areas during the delay (c) and response (d) periods. Similarly to b, we evaluated decoder performance across individual time bins and plotted the maximum (d’)2 values attained for each mouse across all time bins during the delay, c, or response, d, periods. Whereas (d’)2 values for stimulus decoding during the delay period were independent of the mouse’s upcoming response (P<0.3; Wilcoxon signed-rank test; N = 6 mice), response period (d’)2 values were significantly greater for ‘Lick’ trials (P<0.03). The latter, higher values of (d’)2 could stem from the divergent neural signals evoked by receipt of a reward or air puff on ‘Hit’ and ‘False Alarm’ trials, respectively. (e–g) Using methods analogous to those in b, we trained consensus decoders of the mouse’s response on ‘Go’ and ‘No-Go’ trials based on neural activity in different cortical areas during the stimulus (e), delay (f), and response (g) intervals. As in b–d, we evaluated decoder performance across individual time bins and constructed plots using the maximum (d′)2 values attained for each mouse across all time bins during the stimulus (0.5–2 s after stimulus onset), e, delay, f, or response g, periods. To determine neural representations of the mouse’s response during the response interval, g, we used data across the full 3-s response interval. Within this interval, the mouse received rewards and aversive air-puffs at variable time points. Thus, a distinct analysis would be needed to separate coding relating to receipt of the rewarding and aversive stimuli from that relating to the mouse’s actions. (d’)2 values for response decoding were greater for ‘Go’ trials during stimulus presentation (P<0.03; Wilcoxon signed-rank test; N = 6 mice), delay (P<0.06), and response (P< 0.06) intervals. These higher (d’)2 values could reflect signals associated with reward prediction, motor planning and action on correctly performed ‘Go’ trials. (h–j) Map of the cortex for the mouse of Fig. 3g–j. Coloured dots mark locations of cells with the greatest contributions to the response decoder score (defined as cells with decoder weights deviating >2 s.d. from mean values) during stimulus (h), delay (i), and response (j) intervals. Because the mouse’s response was only weakly encoded in the neural dynamics on ‘No-Go’ trials (see e–g), we created h–m based on the response decoders found by analysis of ‘Go’ trials. Cells in each brain area are coloured differently, following the colour scheme in m. Scale bars: 1 mm. (k–m) Mean±s.e.m. (N = 6 mice) fractions of neurons in each area that had response decoder weights deviating >2 s.d. from mean values, during the stimulus (k), delay (l), and response (m) intervals. (n) Right, We measured the information (d’)2 conveyed about reward and punishment in each area by studying the neural activity evoked when the mouse licked. To evaluate the encoding of punishment, we compared the mean neural ensemble activity in the first 0.5 s after licks that were punished with air-puffs versus after licks that occurred during timeout periods and that elicited neither punishment nor reward. To evaluate reward encoding, we compared the mean neural ensemble activity in the first 0.5 s after licks that occurred during timeouts versus after licks triggering a reward. Both punishment and reward were represented to varying extents across the different areas. Notably, these representations could relate to any aspect of the rewarding or aversive experience, such as the experience of receiving or blinking in response to an aversive air-puff or receiving or tasting a reward. Left, As a control, we performed the same calculations as for the right panel but using neural activity that occurred within the 0.5 s intervals just before licks. As expected, during these periods there was notably less information encoded about upcoming rewards or punishments than about rewards or punishment the mouse has just received. (o) A graph of the s.d. of (d’)2 values for each cell (individual data points) across all days of the study, for every cell with a significant (P<0.01) d’ value for trial-type encoding on at least one day, as a function of the cell’s weight in the across-day common decoder. Decoder weights are normalized by the maximum weight in each mouse. Results show that cells can have stable or variable coding properties, irrespective of their decoder weights. Nevertheless, coding variability generally increases for cells with larger weights, as shown by the red line, which plots the mean s.d. in (d’)2 values, averaged over all cells within x-axis bins of 0.1.
Extended Data Fig. 5 Information-limiting noise correlations and coding redundancy peaked just after stimulus onset and then declined for the rest of stimulus presentation.
(a) The fidelity with which stimulus identity could be decoded from neural ensemble activity saturated for large (>2000) populations of cells, for real (purple curves) but not trial-shuffled (black curves) datasets. To study ensembles of each size (x-axis), we randomly chose 100 different subsets of cells from the entire pool of neurons imaged across all areas. We then trained and tested optimal linear Fisher decoders using the neural activity within [0.4 s, 0.5 s] after stimulus onset on correctly performed trials. We quantified decoding performance using (d′)2, which relates to the Fisher information the neural dynamics conveyed about the trial-type. Each curve shows data from one mouse. Whereas (d′)2 saturated for large neural populations in real data, this did not occur for trial-shuffled datasets in which correlated fluctuations were scrambled. Shading: s.d. across all 100 subsets of cells for each ensemble size. Inset: Magnified view near the graph origin for one mouse. (b) Using the methods of a, we assessed how well optimal linear decoders could discriminate Go and No-Go trials. Plots show mean (d′)2 values for this discrimination as a function of neural ensemble size and for different time bins, averaged over N = 6 mice. The size of the cell ensemble at which (d′)2 saturated rose substantially with time during stimulus presentation but stayed relatively constant during the delay and response periods. (d′)2 values are normalized relative to their maximum (saturating) value at each time bin. Ensemble size values are normalized relative to the total number of cells recorded in each mouse. (c) Plots like those of b, for individual mice during stimulus presentation. Data are shown only for time bins in which (d′)2 values were significantly greater than for control datasets in which the trial-type labels were randomly shuffled (P<0.01; permutation test; N = 710–1340 trials). (d) Mean±s.e.m. (N = 6 mice) Ca2+ event rates per time bin (0.1 s duration) for all neurons on correctly performed Go and No-Go trials. These event rates had near identical time dependencies on trials of the two types, but the temporal variations were distinct from those of decoder score fluctuations (Fig. 4b) or correlated fluctuations in cells’ dynamics (panel f). Dashed vertical lines in d–f demarcate stimulus, delay and response periods of the trial structure. (e) Time dependence of the mean Fano factor, determined for each mouse by computing for each cell the ratio of the variance in the cell’s Ca2+ event rate to its mean Ca2+ event rate, on correctly performed trials. Shading: s.e.m. values (N = 2236-5292 cells). Legend also applies to f and g. (f) Noise correlations between pairs of cells with similar stimulus tuning rose sharply after stimulus onset, peaked ~0.2 s after stimulus onset, and then decayed to baseline values. Each coloured trace shows the mean absolute value of noise correlation coefficients for all pairs of similarly tuned cells across all imaged areas in each mouse. (g) Cross-correlation functions between the dynamics of absolute noise correlations across pairs of cells, shown in f, and the Fano factor, shown in e, as determined for each mouse over the 2-s-stimulus period. The graph shows that changes in pairwise noise correlation coefficients were negatively correlated with and most predictive of upcoming variations in the Fano factor with a lead time of ~200 ms. Shading: s.e.m. values (N = 10–20 time bins for each abscissa value). (h) Plot of the mean time-dependent rate (blue trace) of Ca2+ events in Go-stimulus-tuned neurons on Go trials and No-Go-stimulus-tuned neurons on No-Go trials, averaged over both cell-types and N = 6 mice. Also shown is the mean absolute noise correlation coefficient (red trace) for pairs of similarly tuned neurons, computed as in f for the same 6 mice. Notably, changes in noise correlation coefficient levels peaked sooner after stimulus onset than Ca2+ activity rates of tuned cells. After reaching their peak values, noise correlation coefficients declined back to baseline values by stimulus offset, whereas Ca2+ activity rates did not. These differences make it hard to explain the dynamics of noise correlation coefficients as resulting simply from changes in neural activity rates. Shading: s.e.m. across 6 mice. (i) Plot showing the change in information encoded by the neural ensemble if one cell were to become silent, assessed using instantaneous decoders. Each dot denotes the result from one time bin. (As shown in c and f, noise correlation coefficients vary with time following stimulus onset). Results for trial-shuffled data, in which correlated fluctuations were scrambled, are denoted with crosses and reveal a greater sensitivity to loss of one neuron. (j) Left, Traces of mean absolute noise correlation coefficients as a function of time during stimulus presentation, determined as in f for cell pairs in primary visual cortex (V1; blue trace), secondary cortical visual areas (areas LV, MV and PPC; red trace) or non-visual cortical areas (areas A, S, M and RSC; black trace). Right, Traces of mean absolute noise correlation coefficients between pairs of coding neurons located in different brain areas. The rise in noise correlations for similarly tuned cells in visual cortex is greater than that for cells outside visual cortex (P<0.03; Wilcoxon signed-rank test; N = 6 mice). Shading: s.e.m. across N = 6 mice. (k) We calculated the covariance in the neurons’ responses on each trial-type and on each day. We then averaged the covariance matrices for the two trial-types and computed the top 3 eigenvectors for each day. Left, A plot showing the similarity between the pairs of different subspaces (Methods), each defined by the top 3 eigenvectors of the noise covariance matrix on each day of experimentation. The matrix row and columns labelled ‘C’ is for the noise covariance matrix computed for the set of all trials across all days. Right, As control, we computed the subspace similarities for trial-shuffled datasets in which each neuron’s responses were permuted across trials with the same stimulus. Overall, noise covariance structure in the real data was significantly similar across days, to a degree much beyond that in shuffled datasets.
Extended Data Fig. 6 The discriminability of the two stimuli based on their evoked neural dynamics fluctuated trial-by-trial in a way that was highly correlated between cortical areas.
(a) Example scatter plot for an individual mouse in which the instantaneous stimulus decoder scores based on the activity patterns of cortical area PPC are plotted against those for cortical area RSC. Each data point shows results for an individual trial, at 0.5 s after stimulus onset, for Go trials (blue data points) or No-Go trials (black data points). Stimulus decoder scores for the two brain areas exhibit positively correlated trial-to-trial fluctuations. (b) Traces showing the mean time-dependent correlations of the fluctuations in instantaneous stimulus decoder scores for 8 different cortical areas and each of the other 7 brain areas within the imaging field-of-view. For most pairs of brain areas, these correlated noise fluctuations in decoder scores attained their maximum shortly after stimulus onset and then gradually decayed. Decoder training and testing was limited in this analysis to trials that the mice performed correctly. Shading: s.e.m. over N = 6 mice. Vertical dashed lines demarcate the stimulus presentation, delay and response intervals. (c) Two plots showing examples of stimulus-coding cells whose responses were modulated by the mouse’s response. Each plot shows the mean rate of Ca2+ events in an individual neuron, as a function of time relative to stimulus onset at t = 0, for the 4 different trial-types. The cell of the top plot is from area MV, and the cell of the bottom plot is from PPC. Both cells had P-values of <0.01 for stimulus-coding on Lick and No-Lick trials, and also had P < 0.01 for response-coding on GO-trials). We determined P-values through comparisons to trial-shuffled datasets (1000 different sub-samplings and random permutations of trials using equal numbers of trials of both stimulus- or response-types). The separation between the traces for Hit and Miss trials shows the extent of response-related modulation on trials with a Go stimulus. Shading: s.e.m. over trials (410 Hit trials, 218 Miss trials, 665 Correct Rejection trials, 100 False Alarm trials). (d) To determine if the elevated correlated noise fluctuations along the stimulus-coding direction within the interval [0.2 s, 0.5 s] after stimulus onset (when correlations were at their peak) reflects choice information relating to the formation of a motor response plan, we computed for each stimulus-type the proportion of the neural activity variance along the stimulus-coding direction that co-varied with the mouse’s upcoming motor response. The results show that only a tiny percentage (0.5% on average) of the variations in stimulus-coding can be explained as reflecting the mouse’s decision or response. Blue-shaded points denote data from individual mice. Red points are averages across mice. See also Fig. 5e. (e) Peak values of the time-dependent decoder score noise correlations (r), determined as in b, for all pairs of imaged brain areas for an example mouse, using either the data from each of five different imaging sessions, or the aggregated set of data from all imaging sessions. Fluctuations of decoder scores were correlated between sensory cortical areas during all recording sessions. The same general pattern of correlations between brain areas was visible in every session.
Extended Data Fig. 7 Canonical correlation noise modes during the visual stimulation period for 28 different pairs of cortical areas.
(a) Multiple ensembles of neurons from different cortical areas had strongly correlated noise fluctuations during visual stimulus presentation. By performing a CCA on cells’ mean-subtracted activity traces for each trial-type, we identified multiple modes of significantly correlated noise modes (P < 0.01; comparisons of real vs. trial-shuffled data using the permutation test; N = 710–1340 trials) that were shared across 28 different pairs of cortical areas (abbreviated as in Fig. 1). Plots show mean ± s.e.m. (N = 6 mice) correlation coefficients for the first 20 pairs of CCA noise modes for all pairs of brain areas, as determined from validation datasets that were held out from the training datasets used to identify the CCA noise modes (Methods). (b, c) In each cortical area, ~70–90% of the neurons that contributed substantially to the largest CCA noise mode were distinct from the cells that contributed to the second-largest mode. A cell was considered to contribute substantially to a CCA noise mode if its weight in the CCA mode population vector was >2 s.d. above or below the ensemble mean. (b) The mean ± s.e.m. (N = 6 mice) number of cells that contributed substantially to both the first and second CCA noise modes in each brain area, normalized by the total number of cells that contributed substantially to either of these two modes and averaged over all pairings with the other 7 brain areas. (c) Distributions of the number of simultaneously active neurons in each time bin of the stimulus presentation period for the largest five CCA noise modes shared between V1 and the other 7 cortical areas. (d) Mean correlation coefficients (N = 6) for neural activity in the first CCA noise mode shared between the 28 different pairs of cortical areas, for validation (top left) and training (top right) datasets, and on the set of No-Go (bottom left) and Go (bottom right) trials. The similarity of the noise correlation coefficients for all 4 subsets of trials suggests that correlated activity exists in these modes irrespective of the trial-type and that the results are not due to overfitting. (e) Highly correlated noise fluctuations between cortical areas cannot simply be explained as resulting from the activity patterns of cells on the borders between pairs of cortical areas. We repeated the analysis in (a) for all pairs of areas, while discarding the activity traces of cells in each area closer than 60 μm to the boundary of the other area identified by retinotopic mapping. The plot shows the resulting mean ± s.e.m. (N = 6 mice) correlation coefficients for the CCA noise mode fluctuations between V1 and other cortical areas.
Extended Data Fig. 8 The canonical correlation noise modes before stimulus onset were distinct from those after stimulus onset, which were task-related.
(a) During the inter-trial interval (ITI), there were significantly correlated noise fluctuation modes that were shared between cortical areas. However, these modes were not the same as the shared noise fluctuations that arose at stimulus onset. The plots show the mean (N = 6 mice) time courses of the correlation coefficients for the first- and second-largest noise modes shared between 28 different pairs of brain areas (pairs denoted via the graph titles and the colour legend at far right), as found by applying CCA separately to ITI periods (–2 < t < 0) and visual stimulation periods (2 > t > 0). Dashed traces, with and without open circles, respectively show the correlation coefficients for the first and second shared noise modes as identified during ITI periods. Solid traces, with and without open circles, respectively show the correlation coefficients for the first and second share noise modes as identified during stimulus periods. At stimulus onset (t = 0), correlated fluctuations declined within the CCA noise modes identified during ITI periods, whereas correlated fluctuations within the modes identified during the task substantially increased. (b) CCA noise modes found during stimulus periods differ from those found during ITI periods, as shown by the cross-correlation coefficients between the CCA noise modes found for each pair of brain areas before vs. after stimulus onset. The plots show these cross-correlation coefficient values for the largest 5 modes for each pair of brain areas. To compute these coefficients, for each mouse we created 200 different random assignments of half of the trials into a training set and half of the trials into a validation set. Using 100 of these random assignments, we determined CCA noise modes for the ITI period. Using the other 100 assignments, we determined CCA noise modes for the task period. For each entry in the plots, we plotted the mean value of the cross-correlation coefficient, averaged across all 10,000 pairings of one mode from the ITI period and one from the stimulus period, and across 6 different mice. Within each plot, row labels designate the brain area for which we computed the cross-correlation coefficient; column labels designate the area with which the row area was paired in the CCA. (c) As a control analysis for the results of (b), we examined the variability in our estimates of the largest 5 CCA noise modes during the stimulus period. To do this, we computed for each mouse the correlation coefficients between the CCA modes determined from 100 different random assignments of trials into training and validation sets. This showed that most CCA modes are stable during the stimulus presentation period. For each entry in the plots, we plotted the mean value of the cross-correlation coefficient, averaged across all 9,900 pairings of two different mode determinations from the stimulus period, and across 6 different mice. Within each plot, row labels designate the brain area for which we computed the cross-correlation coefficient; column labels designate the area with which the row area was paired in the CCA. The results show that the relative lack of stability exhibited in (b) between CCA noise modes before versus after stimulus onset is not simply due to the statistical variability in the determination of CCA noise modes. (d) In each imaged brain area, we performed a principal component analysis (PCA) of the noise fluctuations around the mean stimulus-evoked responses, averaged over both stimuli. For each brain area, we then computed the correlation coefficients between the modes identified by PCA and those identified by CCA with each of the other 7 brain areas. The results show that fluctuation modes identified by PCA are highly distinct from those found by CCA, indicating that PCA can be incapable of detecting correlated fluctuations between brain areas. (e) Analogous plots to those in (d), except that we performed the PCA over the aggregated set of all brain areas. (f) Plots analogous to those in Fig. 5e, except that results are shown for all pairs of brain areas, rather than averaged across all pairs of sensory areas.
Extended Data Fig. 9 Computational simulations of network dynamics show that the global CCA mode likely reflects a common signal that is broadcast to all the imaged cortical areas.
(a) For the real experimental data, the graphs show the time dependence of the information, (d’)2, encoded about stimulus identity within CCA modes 2–10 in each brain area, plotted as a function of time relative to stimulus onset. (We omitted the first CCA mode, which does not convey stimulus information, Fig. 5d, e). To compute (d’)2 we trained consensus decoders based on the neural activity in each brain area during the stimulus presentation period of correctly performed trials. We then projected the neural dynamics onto each of the CCA modes and used the resulting 9-dimensional activity data to train and test instantaneous decoders of the stimulus identity. The vertical dashed lines indicate the stimulus onset. (b) To explore the patterns of interconnectivity that can give rise to a global CCA noise mode, we simulated neural activity within a range of small world networks and systematically varied the extent and randomness of the inter-connections between pairs of brain areas (Methods). The schematic shows 3 example small world model networks with unidirectional connections between 11 brain areas. Each node denotes one brain area with 500 neurons. The parameter K is the ‘in-degree’, i.e. the number of projections received by each brain area. The parameter P determines the probability that the brain area sending a projection is randomly reassigned to a node outside the K nearest neighbours of the recipient brain area. The distribution of connection weights between areas was set so as to approximately match the canonical correlation coefficients observed in the real cortical recordings (Methods). A wide range of these models exhibited CCA modes among all pairs of brain areas that resembled the patterns of correlated activity fluctuations in our in vivo recordings of neural activity (panel c). However, no model had a global CCA mode, as each pair of brain areas generally had a unique set of cofluctuations distinct from those in other pairs of brain areas (panel d). (c) Canonical correlation coefficients for the strongest CCA modes between all pairs of 11 areas, plotted for different values of K and P. Strongly correlated CCA fluctuations were observed between all pairs of areas in most of the simulations. (d) Correlation coefficients for the first CCA modes between one simulated brain area and each of the other 10 brain areas, plotted as in Fig. 5a. Even when strongly correlated CCA modes exist between all pairs of areas, as shown in (c), the neural ensembles comprising these modes are largely unique and do not establish a global mode—unlike in our actual recordings (Fig. 5a) in which the first CCA mode was global and independent of the pair of brain areas chosen for CCA. These results suggest that global CCA modes may be inconsistent with information transmission through a small-world architecture. (e) The number of cells in each simulated brain area that had their first PCA weights >2 s.d. away from the mean value. Even though the simulated small world networks lacked a global CCA mode, the first mode identified by principal components analysis (PCA) was widely distributed across brain areas. Thus, the existence of distributed PCA modes does not imply the existence of a global CCA mode. (f, g) Schematic, f, of a simulated neural network (Methods) in which information about the visual stimulus is transmitted via separate channels to different higher-order cortical areas, whereas information about the sensory decision is broadcasted in parallel to these higher-order areas. The strengths of neural connections from the early visual area and each of the two higher-order areas were chosen randomly from a Gaussian distribution. The matrix of neural connections between each pair of brain areas had a rank between 1–10. g, Correlation coefficients between CCA modes in simulated cortical areas. In contrast to small-world connectivity, networks in which a single source broadcasted a common signal to multiple brain areas did have a global CCA mode, as in cortex (Fig. 5a). These results suggest the global CCA mode in cortex reflects the widespread distribution of a common signal conveying information about the mouse’s upcoming response to all imaged brain areas, rather than via separate inter-area connections. (h, i) Normalized values of (d’)2 determined for the simulated network of (f) for distinguishing between the two different stimuli, (h), or decisions, (i), plotted for each of the 10 largest CCA modes between all pairs of areas receiving input from the Early Visual Area. Results are shown separately for networks with neural connection matrices of different ranks. Results are averaged across 25 different networks with similar architecture. Shading: s.e.m. across the 3 different simulated areas, Areas A, B and C. Fig. 5e shows similar results for the real experimental data.
Supplementary information
Supplementary Information
Mathematical analyses regarding neural fluctuations on two timescales and decoders with robustness to both types of variations.
Supplementary Video 1
Fluorescence Ca2+ activity in an awake behaving mouse. A fluorescence video of Ca2+ dynamics of layer 2/3 neocortical pyramidal neurons expressing GCaMP6f in an awake behaving mouse. The data were recorded at 20 Hz and are played back at 4× real speed. The field of view is 4 mm × 4 mm.
Rights and permissions
About this article
Cite this article
Ebrahimi, S., Lecoq, J., Rumyantsev, O. et al. Emergent reliability in sensory cortical coding and inter-area communication. Nature 605, 713–721 (2022). https://doi.org/10.1038/s41586-022-04724-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04724-y
This article is cited by
-
Behavior-relevant top-down cross-modal predictions in mouse neocortex
Nature Neuroscience (2024)
-
A unifying perspective on neural manifolds and circuits for cognition
Nature Reviews Neuroscience (2023)
-
Representations in human primary visual cortex drift over time
Nature Communications (2023)
-
Residual dynamics resolves recurrent contributions to neural computation
Nature Neuroscience (2023)
-
Angular gyrus: an anatomical case study for association cortex
Brain Structure and Function (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.