Abstract
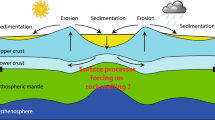
It is widely recognized that collisional mountain belt topography is generated by crustal thickening and lowered by river bedrock erosion, linking climate and tectonics1,2,3,4. However, whether surface processes or lithospheric strength control mountain belt height, shape and longevity remains uncertain. Additionally, how to reconcile high erosion rates in some active orogens with long-term survival of mountain belts for hundreds of millions of years remains enigmatic. Here we investigate mountain belt growth and decay using a new coupled surface process5,6 and mantle-scale tectonic model7. End-member models and the new non-dimensional Beaumont number, Bm, quantify how surface processes and tectonics control the topographic evolution of mountain belts, and enable the definition of three end-member types of growing orogens: type 1, non-steady state, strength controlled (Bm > 0.5); type 2, flux steady state8, strength controlled (Bm ≈ 0.4−0.5); and type 3, flux steady state, erosion controlled (Bm < 0.4). Our results indicate that tectonics dominate in Himalaya–Tibet and the Central Andes (both type 1), efficient surface processes balance high convergence rates in Taiwan (probably type 2) and surface processes dominate in the Southern Alps of New Zealand (type 3). Orogenic decay is determined by erosional efficiency and can be subdivided into two phases with variable isostatic rebound characteristics and associated timescales. The results presented here provide a unified framework explaining how surface processes and lithospheric strength control the height, shape, and longevity of mountain belts.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data supporting the findings of this study are contained within the article and Supplementary Information.
Code availability
Numerical models are computed with published methods and codes, described in the Methods and Supplementary Information. The code for longitudinality index calculations is available from the corresponding author on request.
References
Beaumont, C., Fullsack, P. & Hamilton, J. in Thrust Tectonics (ed. McClay, K. R.) 1–18 (Springer, 1992).
Willett, S. D. Orogeny and orography: the effects of erosion on the structure of mountain belts. J. Geophys. Res. Solid Earth 104, 28957–28981 (1999).
Whipple, K. X., Kirby, E. & Brocklehurst, S. H. Geomorphic limits to climate-induced increases in topographic relief. Nature 401, 39–43 (1999).
Beaumont, C., Jamieson, R. A., Nguyen, M. H. & Lee, B. Himalayan tectonics explained by extrusion of a low-viscosity crustal channel coupled to focused surface denudation. Nature 414, 738–742 (2001).
Braun, J. & Willett, S. D. A very efficient O(n), implicit and parallel method to solve the stream power equation governing fluvial incision and landscape evolution. Geomorphology 180, 170–179 (2013).
Yuan, X. P., Braun, J., Guerit, L., Rouby, D. & Cordonnier, G. A new efficient method to solve the stream power law model taking into account sediment deposition. J. Geophys. Res. Earth Surface 124, 1346–1365 (2019).
Thieulot, C. FANTOM: two-and three-dimensional numerical modelling of creeping flows for the solution of geological problems. Phys. Earth Planet. Inter. 188, 47–68 (2011).
Willett, S. D. & Brandon, M. T. On steady states in mountain belts. Geology 30, 175–178 (2002).
Beaumont, C., Nguyen, M. H., Jamieson, R. A. & Ellis, S. Crustal flow modes in large hot orogens. Geol. Soc. Spec. Publ. 268, 91–145 (2006).
Whipple, K. X. & Tucker, G. E. Dynamics of the stream-power river incision model: implications for height limits of mountain ranges, landscape response timescales, and research needs. J. Geophys. Res. Solid Earth 104, 17661–17674 (1999).
Dadson, S. J. et al. Links between erosion, runoff variability and seismicity in the Taiwan orogen. Nature 426, 648–651 (2003).
Koons, P. O. The topographic evolution of collisional mountain belts – a numerical look at the Southern Alps, New Zealand. Am. J. Sci. 289, 1041–1069 (1989).
Molnar, P. & England, P. Late Cenozoic uplift of mountain-ranges and global climate change – chicken or egg. Nature 346, 29–34 (1990).
Tucker, G. E. & Bras, R. L. A stochastic approach to modeling the role of rainfall variability in drainage basin evolution. Water Resour. Res. 36, 1953–1964 (2000).
Hartshorn, K., Hovius, N., Dade, W. B. & Slingerland, R. L. Climate-driven bedrock incision in an active mountain belt. Science 297, 2036–2038 (2002).
Whipple, K. X. & Meade, B. J. Orogen response to changes in climatic and tectonic forcing. Earth Planet. Sci. Lett. 243, 218–228 (2006).
Willett, S. D., Schlunegger, F. & Picotti, V. Messinian climate change and erosional destruction of the central European Alps. Geology 34, 613–616 (2006).
Hilley, G. E. et al. Earth’s topographic relief potentially limited by an upper bound on channel steepness. Nat. Geosci. 12, 828–832 (2019).
Baldwin, J. A., Whipple, K. X. & Tucker, G. E. Implications of the shear stress river incision model for the timescale of postorogenic decay of topography. J. Geophys. Res. Solid Earth 108, 2158 (2003).
Egholm, D. L., Knudsen, M. F. & Sandiford, M. Lifespan of mountain ranges scaled by feedbacks between landsliding and erosion by rivers. Nature 498, 475–478 (2013).
Molnar, P. & Lyon-Caen, H. Some simple physical aspects of the support, structure, and evolution of mountain belts. Geol. Soc. Am. Spec. Pap. 218, 179–207 (1988).
Sandiford, M. & Powell, R. Some isostatic and thermal consequences of the vertical strain geometry in convergent orogens. Earth Planet. Sci. Lett. 98, 154–165 (1990).
Zhou, S. H. & Sandiford, M. On the stability of isostatically compensated mountain belts. J. Geophys. Res. Solid Earth 97, 14207–14221 (1992).
Vanderhaeghe, O., Medvedev, S., Fullsack, P., Beaumont, C. & Jamieson, R. A. Evolution of orogenic wedges and continental plateaux: insights from crustal thermal-mechanical models overlying subducting mantle lithosphere. Geophys. J. Int. 153, 27–51 (2003).
Wolf, S. G. & Huismans, R. S. Mountain building or backarc extension in ocean-continent subduction systems: a function of backarc lithospheric strength and absolute plate velocities. J. Geophys. Res. Solid Earth 124, 7461–7482 (2019).
Whipple, K. X. Bedrock rivers and the geomorphology of active orogens. Ann. Rev. Earth Planet. Sci. 32, 151–185 (2004).
Sklar, L. S. & Dietrich, W. E. Sediment and rock strength controls on river incision into bedrock. Geology 29, 1087–1090 (2001).
Molnar, P., Anderson, R. S. & Anderson, S. P. Tectonics, fracturing of rock, and erosion. J. Geophys. Res. Earth Surf. 112, F03014 (2007).
Starke, J., Ehlers, T. A. & Schaller, M. Latitudinal effect of vegetation on erosion rates identified along western South America. Science 367, 1358–1361 (2020).
Ellis, S., Fullsack, P. & Beaumont, C. Oblique convergence of the crust driven by basal forcing -implications for length-scales of deformation and strain partitioning in orogens. Geophys. J. Int. 120, 24–44 (1995).
Batt, G. E. & Braun, J. The tectonic evolution of the Southern Alps, New Zealand: insights from fully thermally coupled dynamical modelling. Geophys. J. Int. 136, 403–420 (1999).
Norris, R. J. & Cooper, A. F. Late Quaternary slip rates and slip partitioning on the Alpine Fault, New Zealand. J. Struct. Geol. 23, 507–520 (2001).
Little, T. A. Transpressive ductile flow and oblique ramping of lower crust in a two-sided orogen: insight from quartz grain-shape fabrics near the Alpine fault, New Zealand. Tectonics 23, TC2013 (2004).
Jiao, R., Herman, F. & Seward, D. Late Cenozoic exhumation model of New Zealand: impacts from tectonics and climate. Earth Sci. Rev. 166, 286–298 (2017).
Herman, F., Cox, S. C. & Kamp, P. J. J. Low-temperature thermochronology and thermokinematic modeling of deformation, exhumation, and development of topography in the central Southern Alps, New Zealand. Tectonics 28, https://doi.org/10.1029/2008TC002367 (2009).
Suppe, J. A retrodeformable cross section of northern Taiwan. Proc. Geol. Soc. China 23, 46–55 (1980).
Brown, D., Alvarez-Marron, J., Schimmel, M., Wu, Y. M. & Camanni, G. The structure and kinematics of the central Taiwan mountain belt derived from geological and seismicity data. Tectonics 31, TC5013 (2012).
Brown, D. et al. How the structural architecture of the Eurasian continental margin affects the structure, seismicity, and topography of the south central Taiwan fold-and-thrust belt. Tectonics 36, 1275–1294 (2017).
Simoes, M. et al. Mountain building in Taiwan: a thermokinematic model. J. Geophys. Res. Solid Earth 112, https://doi.org/10.1029/2006JB004824 (2007).
Van Avendonk, H. J. A. et al. Deep crustal structure of an arc-continent collision: constraints from seismic traveltimes in central Taiwan and the Philippine Sea. J. Geophys. Res. Solid Earth 119, 8397–8416 (2014).
DeCelles, P. et al. Geodynamics of a Cordilleran Orogenic System: The Central Andes of Argentina and Northern Chile (Geological Society of America, 2015).
Replumaz, A., Negredo, A. M., Guillot, S., van der Beek, P. & Villasenor, A. Crustal mass budget and recycling during the India/Asia collision. Tectonophysics 492, 99–107 (2010).
Ingalls, M., Rowley, D. B., Currie, B. & Colman, A. S. Large-scale subduction of continental crust implied by India-Asia mass-balance calculation. Nat. Geosci. 9, 848–853 (2016).
Schmalholz, S. M., Medvedev, S., Lechmann, S. M. & Podladchikov, Y. Relationship between tectonic overpressure, deviatoric stress, driving force, isostasy and gravitational potential energy. Geophys. J. Int. 197, 680–696 (2014).
Burbank, D. W. et al. Bedrock incision, rock uplift and threshold hillslopes in the northwestern Himalayas. Nature 379, 505–510 (1996).
Herman, F. et al. Exhumation, crustal deformation, and thermal structure of the Nepal Himalaya derived from the inversion of thermochronological and thermobarometric data and modeling of the topography. J. Geophys. Res. Solid Earth 115, https://doi.org/10.1029/2008JB006126 (2010).
Oncken, O. et al. in The Andes. Frontiers in Earth Sciences (eds Oncken, O. et al.) 3–27 (Springer, 2006).
Schellart, W. P., Freeman, J., Stegman, D. R., Moresi, L. & May, D. Evolution and diversity of subduction zones controlled by slab width. Nature 446, 308–311 (2007).
Wobus, C. W., Hodges, K. V. & Whipple, K. X. Has focused denudation sustained active thrusting at the Himalayan topographic front? Geology 31, 861–864 (2003).
Kirby, E. & Whipple, K. X. Expression of active tectonics in erosional landscapes. J. Struct. Geol. 44, 54–75 (2012).
Curry, M. E., van der Beek, P., Huismans, R. S., Wolf, S. G. & Muñoz, J. A. Evolving paleotopography and lithospheric flexure of the Pyrenean Orogen from 3D flexural modeling and basin analysis. Earth Planet. Sci. Lett. 515, 26–37 (2019).
Harel, M.-A., Mudd, S. & Attal, M. Global analysis of the stream power law parameters based on worldwide 10Be denudation rates. Geomorphology 268, 184–196 (2016).
Stock, J. D. & Montgomery, D. R. Geologic constraints on bedrock river incision using the stream power law. J. Geophys. Res. Solid Earth 104, 4983–4993 (1999).
Guerit, L. et al. Fluvial landscape evolution controlled by the sediment deposition coefficient: Estimation from experimental and natural landscapes. Geology 47, 853–856 (2019).
Densmore, A. L., Allen, P. A. & Simpson, G. Development and response of a coupled catchment fan system under changing tectonic and climatic forcing. J. Geophys. Res. Earth Sci. 112, F01002 (2007).
Armitage, J. J., Jones, T. D., Duller, R. A., Whittaker, A. C. & Allen, P. A. Temporal buffering of climate-driven sediment flux cycles by transient catchment response. Earth Planet. Sci. Lett. 369, 200–210 (2013).
England, P. & McKenzie, D. A thin viscous sheet model for continental deformation. Geophys. J. R. Astron. Soc. 70, 295–321 (1982).
England, P. & McKenzie, D. Correction to – A thin viscous sheet model for continental deformation. Geophys. J. R. Astron. Soc. 73, 523–532 (1983).
Wobus, C. et al. in Tectonics, Climate, and Landscape Evolution (eds Willett, S. D., Hovius, N., Brandon, M. T. & Fisher, D. M.) 55–74 (Geological Society of America, 2006).
Gleason, G. C. & Tullis, J. A flow law for dislocation creep of quartz aggregates determined with the molten-salt cell. Tectonophysics 247, 1–23 (1995).
Mackwell, S. J., Zimmerman, M. E. & Kohlstedt, D. L. High-temperature deformation of dry diabase with application to tectonics on Venus. J. Geophys. Res. Solid Earth 103, 975–984 (1998).
Karato, S. & Wu, P. Rheology of the upper mantle – a synthesis. Science 260, 771–778 (1993).
Owens, T. J. & Zandt, G. Implications of crustal property variations for models of Tibetan plateau evolution. Nature 387, 37–43 (1997).
Acknowledgements
S.G.W. and X.Y. acknowledge support from TOTAL through the COLORS project. C. Beaumont is thanked for constructive comments on an earlier version of the scaling analysis developed here and for proposing the introduction of the surface process Damköhler numbers.
Author information
Authors and Affiliations
Contributions
S.G.W., R.S.H., J.B. and X.Y. designed the experiments, discussed the results and implications, and wrote the article. With help from R.S.H., J.B. and X.Y., S.G.W. developed the coupling between the tectonic model and the surface process model. S.G.W. conducted the comparison to Nature, and ran and visualized the models.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Kelin Whipple, Greg Houseman and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Model setup with boundary conditions (a), initial landscape with surface process parameters (b), and material legend with properties (c).
a, The model is 1200 km wide, 600 km deep and has a uniform layered material distribution. A zoom into the continental lithosphere with corresponding yield-strength-envelope is shown as insert. Mountain building is modelled by applying a velocity boundary condition on both model sides in the lithosphere. Inflow is balanced by small distributed outflow of material in the sub-lithospheric mantle. The side and lower model boundaries have free slip conditions and the upper surface is free. The thermo-mechanical model is coupled to the surface process model FastScape, which starts out with a fluvial network with maximum 250 m elevation (b). The free surface corresponds to the average FastScape elevation. The initial temperature distribution in the continent corresponds to 1D-thermal steady state and the temperature in the sub-lithospheric mantle follows an adiabatic gradient of 0.4 °C. The side boundaries are insulated and the top and bottom of the model domain have fixed temperatures with respectively 0 °C and 1522 °C. c, Material legend shows colour, scaled flow law, and density of model materials. Blues for syn-contractional sediments alternate every 5 Myr. WQtz is the wet quartz flow law from Gleason and Tullis60; DMD is dry Maryland flow law from Mackwell et al.61; WOl is the wet olivine flow law from Karato and Wu62.
Extended Data Fig. 2 Evolution of Bouyancy Forces.
a–c, Buoyancy force plots for three different timesteps with explanation in (g). The plots show the computed buoyancy force as black/grey lines and the sum of integrated overpressure \({\bar{P}}_{O}\) plus Fint as red stippled lines. The stippled lines frame a typical range of values computed in the foreland crustal column in models 1 and 2, at several timesteps. On average, \({\bar{P}}_{O}\approx {F}_{int}\). d–f, Viscosity field and temperature contours (red) at the end of the shortening phase (25 Myr).
Extended Data Fig. 3 Supplementary growth-only models with variable fluvial erodibility.
a–i, Snapshots of supplementary models 1–9 after 25 Myr of model evolution. Each panel consists of: Zoom into the model domain showing material distribution and temperature contours of the thermo-mechanical tectonic model, map-view landscape from landscape evolution model FastScape, and swath elevation profile of the landscape. Swath profiles have the same scale in a-f, but a different scale in g-i. Top-row models do not reach flux steady state (Type 1); middle-row models reach steady state and are to first order strength-limited (Type 2); bottom-row models reach flux steady state and are erosion-limited (Type 3). Note: Non steady state models exhibit rivers flowing in longitudinal valleys in orogen core, and erosion-limited orogens do not form thrust sheets on the left side. H is the maximum mean elevation plotted as function of time in Extended Data Fig. 4b. Colours of model titles a-i correspond to colours in Extended Data Fig. 4.
Extended Data Fig. 4 Time-dependent evolution of mountain width and height.
a, b, Evolution of mountain width and maximum mean elevation through time for the 9 growth-only models with different fluvial erodibility shown in Extended Data Fig. 3. The mountain width is calculated every 0.5 Myr between the two outermost points above 600 m, or above 15% of maximum mean height (black Type 3 models). Steps in width correspond to new outward-propagating thrusts.
Extended Data Fig. 5 The influence of crustal rheology.
a, b, Evolution of mountain width and maximum mean elevation through time for three models with different fluvial erodibility and low crustal strength. Colours are the same in both plots. Mountain width is calculated every 0.5 Myr between the two outermost points which are above 600 m, or above 15% of maximum mean height (in MKf20 and MKf20Weak). Steps in width correspond to new outward-propagating thrusts. c–e, Snapshots of models MKf0.5Weak, MKf5Weak, and MKf20Weak after 25 Myr of model evolution. Each panel consists of: Zoom into the model domain showing material distribution and temperature contours of the thermo-mechanical tectonic model (see Extended Data Fig. 1 for material colours), map-view landscape from landscape evolution model FastScape, swath elevation profile of the landscape, and buoyancy force plot. The buoyancy force plot shows one earlier timestep (10 Myr) as a grey line and the sum of integrated overpressure \({\bar{P}}_{O}\) plus Fint as red stippled lines. The stippled lines frame a typical range of measured values. On average \({\bar{P}}_{O}\approx {F}_{int}\); \({\bar{P}}_{O}\) and Fint are computed in the foreland crustal column in models MKf0.5Weak and MKf5Weak, at several timesteps.
Extended Data Fig. 6 Influence of variable structural style (decoupled thick- and thin-skinned tectonics).
a, b, Evolution of mountain width and maximum mean elevation through time for three models with different fluvial erodibility and with a shallow crustal decoupling horizon (“salt" layer). Colours are the same in both plots. The mountain width is calculated every 0.5 Myr between the two outermost points above 600 m, or above 15% of maximum mean height (in MKf20 and MKf20Salt). Steps in width correspond to new outward-propagating thrusts. c–e, Snapshots of models MKf0.5Salt, MKf5Salt, and MKf20Salt after 25 Myr of model evolution. Each panel consists of: Zoom into the model domain showing material distribution and temperature contours of the thermo-mechanical tectonic model (see Extended Data Fig. 1 for material colours, purple is the weak layer), map-view landscape from landscape evolution model FastScape, swath elevation profile of the landscape, and buoyancy force plot. The buoyancy force plot shows one earlier timestep (10 Myr) as a grey line and the sum of integrated overpressure \({\bar{P}}_{O}\) plus Fint as red stippled lines. The stippled lines frame a typical range of measured values. On average, \({\bar{P}}_{O}\approx {F}_{int}\); \({\bar{P}}_{O}\) and Fint are computed in the foreland crustal column in models MKf0.5Salt and MKf5Salt, at several timesteps.
Extended Data Fig. 7 Analytical scaling relationship for decay phase II - effectively local isostatic rebound.
a–f, Elevation-time plots of FastScape-only models with low and high erodibility, variable orogen width and variable initial orogen height. Each sub-figure shows the evolution of topography and corresponding analytical solution of four models starting with the same width but with different initial heights. Uplift in these models is local-isostatic \((U=(1-\rho {\prime} )\times \dot{e})\), erosion follows the (extended) stream-power law with the same parameters as used in the coupled models. U is the uplift rate, \(\dot{e}\) is the erosion rate, and \(\rho {\prime} \) is the isostatic compensation factor (see Supplementary Information). g, Shows evolution of maximum mean topography of the three models presented in the main text (Figure 1) with corresponding analytical solutions. The analytical solution is derived in the supplemental material. We see that a wider orogen and lower erodibility lead to slower decay; a lower initial starting height corresponds to a shift in time on the decay curve. The latter is displayed in (h). All models show good fit between analytical solution and evolution of topography.
Extended Data Fig. 8 Non-dimensional Surface Processes Damköhler numbers and Beaumont number.
a, Theoretical box model that describes the mechanics of surface processes with fluxes between different hypothetical reservoirs. b, Definition of the four Surface Processes Damköhler numbers (DaSP) determining the mechanics and efficiency of surface processes. c, Definition of a new non-dimensional number, termed Beaumont-number (Bm) that determines the interaction between surface processes and tectonics. NTec is the non-dimensional number determining topographic growth, here the crustal Argand number Ar in case of collisional orogens, Ne is the uplift-erosion number.
Extended Data Fig. 9 Longitudinality index in modelled orogens (a,b) and natural examples (d-f), steepness index of modelled orogens (h).
a, b, 2D longitudinality index (LI) plots of Models 1 and 2 showing the FastScape elevation as grey-shade in the background, the LI of each source point (A = 1 × 105 m2) of a river as colour coding, and the corresponding rivers as light-grey and transparent overlay. The black lines are the orogen boundaries corresponding to 300 m average elevation. c–f, DEM and (LI) plots for Taiwan (Tw), the Southern Alps of New Zealand (SANZ), Himalaya-Tibet (Him), and the Central Andes (And). The DEMs show elevation as colour coding, the manually picked orogen boundaries as black lines, and a stippled box outlining the LI plots. The LI plots show elevation as grey-shade in the background, each LI of a source point (A = 1 × 105 m2) of a river as colour coding. g, Box-and-whisker plots show the full LI datasets with boxed first and third quartile, whiskers expanding to the minimum and maximum of the datasets (+1.5 IQR), median as green line, mean as green dot, and outliers as grey circles. The grey, stippled line corresponds to a value of 1.5, which is roughly the maximum value of model 2. h, Swath profile of steepness indices of models 1 and 2 at the end of shortening and during orogenic decay. Bold line shows median, shaded area frames value range (Methods).
Extended Data Fig. 10 Digital elevation models, swath profiles, and geological cross sections of the Southern Alps of New Zealand, Taiwan, Himalaya-Tibet and Central Andes.
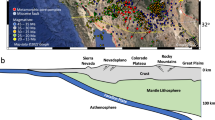
The swath profiles are created in the vicinity of the cross sections, oranges are crust, greys are lithospheric mantle, and vc is the convergence velocity related to crustal thickening. a, Cross section modified from Little33 and Herman et al.35. b, Cross section modified from Brown et al.37 and Van Avendonk et al.40, lc is lower crust, oc is oceanic crust, so are syn-orogenic sediments, sr are pre-orogenic syn-rift sediments, LA is the Luzon Arc, LV is the longitudinal valley, orange color is crustal rocks. c, Cross section modified from Owens & Zandt63. Yellow color is lower crust, orange is crust from the pro-plate, light-orange is Tibetan retro-plate crust. The light-grey lithospheric mantle is possibly removed. d, Cross section modified from DeCelles et al.41. The additional swath profiles II and III show that the actively shortening Central Andes reach similar heights independent of orogen width.
Supplementary information
Supplementary Information
(1) An explanation of the supplementary model animations. (2) An extended methods section explaining the modelling basics and setup choices of the thermo-mechanical landscape evolution model. (3) A detailed description of the supplementary models. (4) The derivation of the scaling relationship between surface processes and tectonics during orogenic growth. (5) A comprehensive comparison between model inferences and the natural examples discussed in the text. (6) The derivation of the scaling relationship between surface processes and tectonics during orogenic decay.
Supplementary Information
Legends for the Supplementary Videos.
Supplementary Videos
A zip file containing 21 animations of the presented numerical models; see separate file for legends.
Rights and permissions
About this article
Cite this article
Wolf, S.G., Huismans, R.S., Braun, J. et al. Topography of mountain belts controlled by rheology and surface processes. Nature 606, 516–521 (2022). https://doi.org/10.1038/s41586-022-04700-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04700-6
This article is cited by
-
Drainage divide migration and implications for climate and biodiversity
Nature Reviews Earth & Environment (2024)
-
Thermodynamics of continental deformation
Scientific Reports (2023)
-
3D geodynamic-geomorphologic modelling of deformation and exhumation at curved plate boundaries: Implications for the southern Alaskan plate corner
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.