Abstract
Topology in quantum many-body systems has profoundly changed our understanding of quantum phases of matter. The model that has played an instrumental role in elucidating these effects is the antiferromagnetic spin-1 Haldane chain1,2. Its ground state is a disordered state, with symmetry-protected fourfold-degenerate edge states due to fractional spin excitations. In the bulk, it is characterized by vanishing two-point spin correlations, gapped excitations and a characteristic non-local order parameter3,4. More recently it has been understood that the Haldane chain forms a specific example of a more general classification scheme of symmetry-protected topological phases of matter, which is based on ideas connected to quantum information and entanglement5,6,7. Here, we realize a finite-temperature version of such a topological Haldane phase with Fermi–Hubbard ladders in an ultracold-atom quantum simulator. We directly reveal both edge and bulk properties of the system through the use of single-site and particle-resolved measurements, as well as non-local correlation functions. Continuously changing the Hubbard interaction strength of the system enables us to investigate the robustness of the phase to charge (density) fluctuations far from the regime of the Heisenberg model, using a novel correlator.
Similar content being viewed by others
Main
Topological phases of matter often share a deep connection between their bulk and edge properties8,9. In the case of the Haldane chain, the bulk exhibits a hidden antiferromagnetic (AFM) order characterized by AFM correlations interlaced with an arbitrary number of Sz = 0 elements, where Sz denotes the spin component in the z-direction. This pattern can only be revealed through non-local string correlations that are sensitive to the local spin states, which, however, require detection of the quantum many-body system with microscopic resolution. Although this was not possible in early experiments on spin-1 chains, evidence for a spin gap, as well as spin-1/2 localized edge states, was found using neutron scattering10,11 or electron resonance experiments12,13 while not directly probing this hidden order or spatially resolving the edge states. Recent developments in quantum simulations enable one to go beyond such solid-state bulk measurements by observing quantum many-body systems with single-site resolution14,15,16,17,18 and in a fully spin- and density-resolved way19,20. This provides a rich diagnostic tool to obtain a direct microscopic picture of the hidden order in experiments21,22. The power of this technique has also been demonstrated recently in a study that was able to reveal a symmetry-protected topological (SPT) phase in the hardcore boson Su–Schrieffer–Heeger (SSH) model using Rydberg atoms23. Here we expand on those results by realizing a finite-temperature version of the Haldane phase in a spin system with tuneable coupling strength, system size and controlled charge fluctuations. We show this by measuring both topological and trivial string order parameters.
An instructive way to engineer the Haldane phase in systems of spin-1/2 fermions is on the basis of the AKLT model4,24, in which a spin-1 particle is formed out of two spin-1/2 particles. Thus, spin-1/2 ladder systems emerge as an experimentally realizable platform for the Haldane phase. Whereas a natural implementation with spin-1 particles on individual rungs requires ferromagnetic rung couplings and antiferromagnetic leg couplings, a much wider variety of couplings in spin-1/2 quantum ladders feature the Haldane phase25,26. This includes the antiferromagnetic Heisenberg case, which we realize here as the strong-interaction limit of the Fermi–Hubbard model.
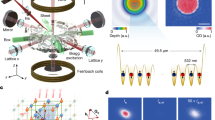
In our experiment, we prepare such ladders by adiabatically loading a spin-balanced mixture of the two lowest hyperfine states of 6Li into an engineered lattice potential (Methods). As illustrated in Fig. 1a, we realize four isolated two-leg ladders with a variable number (L) of unit cells (where L is therefore also equivalent to length), surrounded by a low-density bath of particles27. The unit cells are chosen to be either along the rungs of the ladders (vertical unit cell, Fig. 1b) or along the diagonals (diagonal unit cells, Fig. 1c). The edges of the ladders are then engineered to match the choice of unit cell: straight edges are chosen for vertical unit cells, whereas one site is blocked on each edge in the case of diagonal unit cells. The atoms in the lowest band of the optical lattice are well described by the Fermi–Hubbard model, with tunnelling energies, \({t}_{\parallel }\) (chain), \({t}_{\perp }\) (rung), and on-site interactions U. For half-filling and at strong \(U/{t}_{\parallel ,\perp }\approx 13\), used throughout most of our experiments (see Methods for details), density fluctuations are suppressed and the spin ladder realizes the Heisenberg model28 with Hamiltonian:
a, Realization of tailored spin-1/2 ladders in a single plane of a 3D optical lattice with a potential shaped by a DMD. The dilute wings of the potential are well separated from the homogeneous ladder systems. Using quantum gas microscopy, we obtain fully spin- and density-resolved images of the system. The inset shows a single-shot fluorescence image of the prepared ladder without spin resolution. b, c, Connecting spin-1/2 ladders to integer-spin chains by grouping pairs of spins in unit cells. For diagonal unit cells (b) the AFM Heisenberg ladder adiabatically connects to the Haldane spin-1 chain showing spin-1/2 edge states and hidden long-range order (that is, AFM order interspersed with Sz = 0 unit cells). For vertical unit cells (c), the system is in the topologically trivial phase dominated by singlets on the rungs, forming a spin-0 chain. We adapt the edges of the system to match the respective unit cell, that is straight edges for vertical unit cells and tilted edges for diagonal unit cells, which we realize by blocking one site on each end. The energy spectra of the systems grouped by total magnetization Mz display gapped fourfold near-degenerate ground states for the topological configuration and a single ground state for the trivial one. Sketch for L = 7.
with positive leg and rung couplings, \({J}_{\parallel ,\perp }=4{t}_{\parallel ,\perp }^{2}/U\) and the spin-1/2 operators \({\hat{{\bf{S}}}}_{x,y}\) at site (x, y), with A, B denoting the two legs of the ladder.
The topological properties are most easily explained in the limit \({J}_{\perp }\gg {J}_{\parallel }\), where strong spin singlets form along the rungs and the system exhibits an energy gap of \({J}_{\perp }\). The behaviour on the edges of the ladder then depends on how the system is terminated, and therefore on which unit cells have been chosen. For diagonal unit cells (Fig. 1b), two unpaired spin-1/2 particles remain and the many-body system has a fourfold degeneracy that is only weakly lifted by an edge-to-edge coupling, which vanishes exponentially with system size (Supplementary Information). In the trivial case of vertical unit cells (Fig. 1c), all spins pair into singlets and the ground state is unique. These descriptions remain valid even for weaker \({J}_{\perp }/{J}_{\parallel }\), where the singlet alignment may change between vertical and horizontal, but any line between two rungs cuts an even number of singlets29,30.
To make the analogy between the spin-1/2 ladder and the Haldane integer chain more apparent, we switch to a description in terms of total spin per kth unit cell, \({\hat{{\bf{S}}}}_{k}={\hat{{\bf{S}}}}_{k,{\rm{A}}}+{\hat{{\bf{S}}}}_{k,{\rm{B}}}\), where the indices (A, B) indicate the two spin-1/2 particles in the same unit cell, making an integer spin. In the diagonal unit cell such a system shows a high (≥80%) triplet fraction26 (Supplementary Information). We note that this spin ladder can be adiabatically connected to a spin-1 chain by including ferromagnetic couplings within the unit cell25. However, having a high triplet fraction is not essential for having a well-defined Haldane phase, as both systems share the same universal SPT features26.
The defining property of the Haldane SPT phase is that it is an integer-spin chain with spin-1/2 edge modes: the bulk SO(3) symmetry is said to fractionalize into SU(2) symmetry at the edge. It has no spontaneous symmetry breaking and thus the spin correlation function \(\langle {\hat{S}}_{k}^{z}{\hat{S}}_{k+d}^{z}\rangle \) is short range. Instead, the aforementioned symmetry fractionalization6,7 can be detected in the bulk using string order parameters3,31:
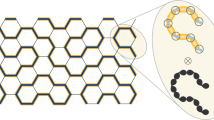
with an on-site symmetry \({\hat{U}}_{l}\) and endpoint operator \({\hat{{\mathscr{O}}}}_{k}\), where l denotes the unit cell and d the string distance (Fig. 2 and Supplementary Information). This correlator probes the transformation behaviour of the bulk under a symmetry \({\hat{U}}_{l}\); for example, a spin rotation around the z axis by π, \({\hat{R}}_{l}^{z}\equiv {\rm{\exp }}({i}{\rm{\pi }}{\hat{S}}_{l}^{z})\). The pure-string correlator \({g}_{{\mathbb{1}},{R}^{z}}(d)\), where \({\hat{{\mathscr{O}}}}_{k}=1\) and \({\hat{U}}_{l}={\hat{R}}_{l}^{z}\), is non-zero for \(d\gg 1\) if the edge does not have half-integer spins31. This is the case for the topologically trivial configuration but not for the Haldane phase, in which the symmetry is fractionalized. The spin-string operator \({g}_{{S}^{z},{R}^{z}}(d)\)(ref. 3), \({\hat{{\mathscr{O}}}}_{k}={\hat{S}}_{k}^{z}\), exhibits the opposite behaviour and is non-zero only in the Haldane phase (see Supplementary Information for details about the symmetries of the Haldane phase). Thus we can identify the Haldane phase by comparing the two string correlators \({g}_{{S}^{z},{R}^{z}}\) and \({g}_{{\mathbb{1}},{R}^{z}}\), and observe opposite behaviour in the two different regimes.
a, The atomic density distribution ⟨\(\hat{n}\)⟩ of ladders with diagonal and vertical unit cells. b, The amplitudes of the spin-string correlator \({g}_{{S}^{z},{R}^{z}}\) (green circles) and the string-only correlator \({g}_{{\mathbb{1}},{R}^{z}}\) (grey squares) observed as a function of the spin distance over d unit cells. The cartoon illustrates the unit cells, the total spin Sz per unit cell and the string correlators for a subsystem with d = 3. In the trivial configuration (rung unit cells), \(|{g}_{{\mathbb{1}},{R}^{z}}(d)|\) is well above zero, whereas \(|\,{g}_{{S}^{z},{R}^{z}}(d)|\) is rapidly vanishing at d > 1. By contrast, for the topological configuration (diagonal unit cells), \(|\,{g}_{{S}^{z},{R}^{z}}(d)|\), shows a long-range correlation, whereas \(|{g}_{{\mathbb{1}},{R}^{z}}(d)|\) is close to zero. In both cases, the two-point spin–spin correlation C(d) decays rapidly to zero as a function of the distance d (insets). The correlators \({g}_{{\mathbb{1}},{R}^{z}},{g}_{{S}^{z},{R}^{z}}\) and C(d) are evaluated for fixed total magnetization \({m}^{z}\) = 0. c, Amplitudes of the rung- and inversion-averaged local magnetizations \(|{m}^{z}(x)|\) plotted as a function of position x along the chains for different \({m}^{z}\). In the unbalanced spin sector of the topological configuration (\({m}^{z}\) = ±1), the result displays a localization of the excess spins at the edges, signalling the presence of edge states. All data were taken with \({J}_{\perp }/{J}_{\parallel }=1.3(2)\). Error bars denote one standard error of the mean (s.e.m.) and are smaller than their marker size if not visible.
Another perspective on \({g}_{{S}^{z},{R}^{z}}\) can be gained by recognizing it as a normal two-point correlator at distance d, which ignores all spin-0 contributions along the way (‘squeezed space’22,32). In the underlying spin-1/2 system, this order stems from N − 1 consecutive rungs dominantly consisting of N − 1 singlets and two spin-1/2 states, which have a combined total spin of +1, 0 or −1.
To observe the characteristics of the SPT phase, we prepare a two-leg ladder of length L = 7 and \({J}_{\perp }/{J}_{\parallel }=1.3(2)\) in both the topological and the trivial configuration. The tailored potential yields a homogeneous filling of the system with sharp boundaries (Fig. 2a), which is characterized by a remaining density variance over the system of 2 × 10−4. To focus on the spin physics, we select realizations with \({N}_{\uparrow }+{N}_{\downarrow }=2L\) per ladder. Additionally, we exclude ladders with an excessive number of doublon–hole fluctuations and do not consider strings with odd atom numbers in the string or the endpoints of the correlator (Methods). We characterize the spin-balanced ladder systems \(({M}^{z}\equiv ({N}_{\uparrow }-{N}_{\downarrow })/2=0)\) by evaluation of the string order parameters, as defined in equation (2). In the topological configuration, we observe fast decay of \({g}_{{S}^{z},{R}^{z}}\) over a distance of approximately one site and a long-range correlation up to d = 6, with a final value of \({g}_{{S}^{z},{R}^{z}}\simeq 0.1\) (Fig. 2b). In contrast, for the trivial configuration, the correlation decays rapidly to zero as a function of the string correlator length. The opposite behaviour is seen for \({g}_{{\mathbb{1}},{R}^{z}}(d)\), demonstrating the hidden correlations expected for both phases.
Furthermore, the two-point spin correlation, \(C(d)\equiv {g}_{{S}^{z},{\mathbb{1}}}(d)=\)\(\langle {\hat{S}}_{k}^{z}{\hat{S}}_{k+d}^{z}\rangle \,,\) yields only the short-range AFM correlation characteristic for a gapped phase (see insets in Fig. 2b). It is interesting to note that at the largest distance in the topological case, C(d = 6) displays a clear (negative) correlation between the two edge spins, despite small correlations at shorter distances. This (classical) correlation confirms the existence of a non-magnetized bulk, such that spins on the edges of the system must be of opposite direction at global Mz = 0.
We probe the edges explicitly by measuring the amplitude of the local rung-averaged magnetization mz(x) as a function of rung position x for different sectors of the ladder magnetization Mz (Fig. 2c). In the case of an imbalanced spin mixture with Mz = ±1, we see that the two end sites exhibit on average a higher magnetization than the bulk rungs in the topological configuration. This is consistent with the bulk of the ground states of both phases forming a global singlet, and only the edges of the topological phase carrying an excess spin-1/2 without energy cost. The measured bulk magnetization can be attributed to finite-temperature effects (Supplementary Information).
The SPT phase is expected to be robust26 on variation of the ratio \({J}_{\perp }/{J}_{\parallel }\), but maintains a finite gap in the system. We realize both the trivial and topological configuration with different \({t}_{\perp }/{t}_{\parallel }\) at almost fixed U and study the string correlators at maximal distance (L − 1) versus \({J}_{\perp }/{J}_{\parallel }\) (Fig. 3a). For the topological configuration with diagonal unit cells, we observe \({g}_{{\mathbb{1}},{R}^{z}}(L-1)\simeq 0\) and \(|{g}_{{S}^{z},{R}^{z}}| > 0\) for all \({J}_{\perp }/{J}_{\parallel }\) with a maximum around \({J}_{\perp }/{J}_{\parallel }\simeq 1.3(2)\) (that is, \({J}_{\perp }/({J}_{\perp }+{J}_{\parallel })\simeq 0.56(4)\)), whereas for the trivial case the role of the correlators is reversed. Both phases continuously connect in the limit of two disconnected chains at \({J}_{\perp }=0\). These observations demonstrate qualitatively all the key predictions of the antiferromagnetic spin-1/2 ladder at temperature T = 0 (ref. 26) and the strengths of the measured correlations are consistent with exact diagonalization (ED) calculations using an entropy per particle \(S/N=(0.3-0.45)\,{k}_{{\rm{B}}}\) (shaded lines in Fig. 3a).
a, The two string order parameters, \({g}_{{S}^{z},{R}^{z}}\) (green) and \({g}_{{\mathbb{1}},{R}^{z}}\) (grey), for both trivial (left) and topological (right) configurations measured as a function of \({J}_{\perp }/({J}_{\perp }+{J}_{\parallel })\). Both \({g}_{{S}^{z},{R}^{z}}\) and \({g}_{{\mathbb{1}},{R}^{z}}\) stay finite in their respective phases and are largely consistent with zero in the other phase. The data were taken at a chain length of L = 5 except for one data point marked by a triangle at L = 7. Shaded curves are the ED results of the two order parameters at finite entropy per particle, S/N = (0.3−0.45) kB and L = 5. The inset shows the measured \({g}_{{S}^{z},{R}^{z}}\) as a function of the chain length L at \({J}_{\perp }/{J}_{\parallel }=1.3(2)\) (that is, \({J}_{\perp }/({J}_{\perp }+{J}_{\parallel })=0.56(4)\)). The decay in the magnitude of the string order parameter with length is expected at finite temperatures in quantitative agreement with ED results (lines) at S/N ≈ 0.4 kB. b, Edge state localization at \({J}_{\perp }/{J}_{\parallel }=1.3(2)\). In the \({m}^{z}\) = ±1 spin sectors of the topological configuration, the unit cell local magnetization \(|{m}^{z}(k)|\) at chain position k shows excess magnetization localized at the edges for different lengths. The black line is a fit to our inversion-averaged data. c, The localization length ξ of the edge states increases with the leg coupling \({J}_{\parallel }\) but saturates at a value set by temperature and system size L = 5. Lines are ED results at S/N = 0.3 kB and 0 kB. The inset shows the independence of ξ with respect to L extracted from the plots in b, as well as ED results for S/N = 0.3 kB. Error bars denote one standard error of the mean (s.e.m) and are smaller than their marker size if not visible.
We reveal these features despite the finite temperature in our system, which would destroy the long-range hidden order in an infinite system. The total entropy in our system is, however, still low enough to yield a large fraction of realizations of the topological ground state. In larger systems, the total number of thermal excitations grows (at fixed entropy per particle) and the non-local correlator \(|\,{g}_{{S}^{z},{R}^{z}}(L-1)|\) decreases (see inset of Fig. 3a), consistent with vanishing correlations in the thermodynamic limit, thus yielding a restriction on our system size at our level of experimental precision and entropy per particle (Supplementary Information). Finite size effects are explored in detail in the Supplementary Information. We note that the difference between the SPT phase and the trivial phase is here clearly shown by considering both \({g}_{{S}^{z},{R}^{z}}\) and \({g}_{{\mathbb{1}},{R}^{z}}\).
To investigate the localization length of the edge states, we evaluate our data for \({m}^{z}\) = ±1 and plot the local magnetization per unit cell \({m}^{z}\)(k) for different system sizes (Fig. 3b). Because of the singlets in the bulk, the excess spin is most likely to be found at the edges of the system. This spin partly polarizes the neighbouring sites antiferromagnetically, leading to an exponentially localized net magnetization with AFM substructure33. The data are well described by the fit function \({m}^{z}(k)={m}_{{\rm{B}}}+{m}_{{\rm{E}}}\left({(-1)}^{k}{{\rm{e}}}^{-k/\xi }+{(-1)}^{L-k-1}{{\rm{e}}}^{-(L-k-1)/\xi }\right)\) with free bulk magnetization mB, edge magnetization mE and decay length ξ. In Fig. 3c, we show how this localization length ξ decreases as we approach the limit of rung singlets, \({J}_{\perp }\gg {J}_{\parallel }\). Comparison with ED lets us identify two regimes: at \({J}_{\perp }\gtrsim {J}_{\parallel }\), the measured ξ drops with larger \({J}_{\perp }\) and coincides with theory independent of temperature, whereas at low \({J}_{\parallel }\) thermal effects dominate, limiting the increase of ξ to three sites for our system (Supplementary Information).
Thus far, we have worked in the Mott limit where density fluctuations can be ignored, such that the spin Hamiltonian, equation (1), is a good effective description of the Fermi–Hubbard ladder. However, it is known that the Haldane SPT phase can be unstable to density fluctuations34,35,36. By reducing \(U/{t}_{\parallel }\), the symmetry in the unit cell in the bulk changes from SO(3) to SU(2), as it now may contain both half-integer and integer total spin. This effectively removes the distinction between bulk and edge (Supplementary Information). This means that the edge mode and string order parameter are no longer topologically non-trivial, which is also manifested in the fact that the two phases can be adiabatically connected by tuning through a low-\(U/{t}_{\parallel }\) regime if one breaks additional symmetries but preserves spin-rotation symmetry34,35,36. In particular, the above string orders lose their distinguishing power: \({g}_{{S}^{z},{R}^{z}}\) and \({g}_{{\mathbb{1}},{R}^{z}}\) will both generically have long-range order away from the Mott limit34.
Intriguingly, despite the breakdown of the above symmetry argument and string order parameter, the Hubbard ladder (with diagonal unit cell) remains a non-trivial SPT phase due to its sublattice symmetry. This symmetry is a direct consequence of the ladder being bipartite (see Supplementary Information for details). It is simplest to see that this protects the SPT phase in the limit U = 0, where the two spin species decouple, such that our model reduces to two copies of the SSH chain37. It is known that such a stack remains in a non-trivial SPT phase in the presence of interactions, namely U ≠ 0 (ref. 38). Moreover, together with the parity symmetry of spin-down particles, \({\hat{P}}_{l}^{\downarrow }\equiv {\rm{\exp }}\left[{i}{\rm{\pi }}\left({\hat{n}}_{l,{\rm{A}}}^{\downarrow }+{\hat{n}}_{l,{\rm{B}}}^{\downarrow }\right)\right]\), it then gives rise to a different string order parameter: the topological phase is characterized by long-range order in \({g}_{{S}^{z},{P}^{\downarrow }}\), whereas it has vanishing correlations for \({g}_{{\mathbb{1}},{P}^{\downarrow }}\), with the roles being reversed in the trivial phase. This novel string order is derived in the Supplementary Information. Remarkably, in the Heisenberg limit, it coincides with the conventional string order parameter used before.
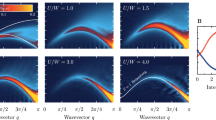
In the topological phase it is meaningful to normalize \({g}_{{S}^{z},{P}^{\downarrow }}\) to \({\tilde{g}}_{{S}^{z},{P}^{\downarrow }}=\eta {g}_{{S}^{z},{P}^{\downarrow }}\) with \({\eta }^{-1}=\langle |{\hat{S}}_{k}^{z}||{\hat{S}}_{k+d}^{z}|\rangle \), which effectively excludes endpoints with spin Sz = 0. Indeed, we find unchanged string correlations \({\tilde{g}}_{{S}^{z},{P}^{\downarrow }}\) and \({g}_{{\mathbb{1}},{P}^{\downarrow }}\) down to the lowest experimentally explored value \(U/{t}_{\parallel }=2.5(2)\) (Fig. 4a, b) and edge state signals down to \(U/{t}_{\parallel }=5.0(3)\) (Fig. 4c). Density matrix renormalization group (DMRG) calculations for \(L\to \infty \) confirm non-zero \({\tilde{g}}_{{S}^{z},{P}^{\downarrow }}\) (L−1) at T = 0 and for all rung-coupling strengths (Fig. 4d), while \({g}_{{\mathbb{1}},{P}^{\downarrow }}(L-1)\) is strictly zero. Owing to the normalization \({\tilde{g}}_{{S}^{z},{P}^{\downarrow }}(L-1)\) goes to 1 for \({J}_{\perp }\gg {J}_{\parallel }\).
a, b, The hidden SPT order is preserved even at low Hubbard interactions, as revealed by the novel string correlators \(|\,{\tilde{g}}_{{S}^{z},{P}^{\downarrow }}(d)\,|\) (green circles) and \(|{g}_{{\mathbb{1}},{P}^{\downarrow }}(d)|\) (grey squares) on the basis of the spin-down parity \({\hat{P}}^{\downarrow }\). \(|\,{\tilde{g}}_{{S}^{z},{P}^{\downarrow }}\,|\) stays non-zero, whereas \(|{g}_{{\mathbb{1}},{P}^{\downarrow }}|\) is consistent with zero for d = L − 1 over the measured interaction range. The same qualitative behaviour is seen in zero-temperature DMRG calculations (shaded line) with \(L\to \infty \). c, Spatial distribution of excess magnetization (\({m}^{z}\) = ±1) for decreasing \(U/{t}_{\parallel }\). Even far away from the Heisenberg regime, the edge state signal remains strong and only diminishes for very weak \(U/{t}_{\parallel }\). d, Map of zero-temperature DMRG \((L\to \infty )\) results for the spin-string correlator in the entire parameter space of the topological phase. It shows a strictly non-zero \({\hat{g}}_{{S}^{z},{P}^{\downarrow }}\) while \({g}_{{\mathbb{1}},{P}^{\downarrow }}(L-1)=0\) everywhere in this phase. The black circles indicate the parameters of the measurements. All experimental data were taken at \({J}_{\perp }/{J}_{\parallel }=1.3(2)\) and L = 5 in the tilted geometry. \({m}^{z}\) = 0 in a, b and d. Error bars denote one standard error of the mean (s.e.m.) and are smaller than their marker size if not visible.
In our work, we realized a finite-temperature version of the topological Haldane SPT phase using the full spin and density resolution of our Fermi quantum gas microscope. We demonstrated the robustness of the edge states and the hidden order of this SPT phase in both the Heisenberg and the Fermi–Hubbard regime. In the future, studies may extend the two-leg ladder to a varying number of legs, in which one would expect clear differences between even and odd numbers of legs39 and topological effects away from half-filling40, or may investigate topological phases in higher dimensions41. Furthermore, the ladder geometry holds the potential to reveal hole–hole pairing42 at temperatures more favourable than in a full two-dimensional system.
Methods
Experimental sequence
In each experimental run, we prepare a cold atomic cloud of 6Li in a balanced mixture of the lowest two hyperfine states (F = 1/2, mF = ±1/2). For evaporation, we confine the cloud in a single layer of a staggered optical superlattice along the z direction, with spacings as = 3 μm and a1 = 6 μm and depths \({V}_{s}=45\,{E}_{{\rm{R}}}^{{\rm{s}}}\) and \({V}_{l}=110\,{E}_{{\rm{R}}}^{{\rm{l}}}\), where ER denotes the recoil energy of the respective lattice. The atoms are harmonically confined in the xy plane and the evaporation is performed by ramping up a magnetic gradient along the y direction20. The final atom number is tuned via the evaporation parameters.
The cloud is then loaded into an optical lattice in the xy plane with spacings ax = 1.18 μm and ay = 1.15 μm, which is ramped up within 100 ms to its final value, ranging from 5ER to 15ER depending on the chosen Hubbard parameters. The scattering length is tuned from 230 aB during evaporation, with aB being the Bohr radius, to its final value ranging between 241 aB and 1,200 aB using the broad Feshbach resonance of 6Li. An overview of the parameters of each dataset is given in Extended Data Table 1. Simultaneously with the lattice loading, a repulsive potential is ramped up, which compensates for the harmonic confinement generated by the curvature of the Gaussian lattice beams and divides the resulting flat area into four disconnected ladder systems along the y direction (see ‘Potential shaping’). We achieve temperatures of \({k}_{{\rm{B}}}T\approx 0.9(3){J}_{\parallel }\) for the parameters in Fig. 2.
For detection, the configuration is frozen by ramping the xy lattices to \(43\,{E}_{{\rm{R}}}^{xy}\) within 250 μs. A Stern–Gerlach sequence separates the two spin species into two neighbouring planes of the vertical superlattice, which are then separated to a distance of 21 μm using the charge pumping technique described in ref. 20. Finally, simultaneous fluorescence images of the two planes are taken using Raman sideband cooling in our dedicated pinning lattice43, with an imaging time of 2.5 s. The fluorescence of both planes is collected through the same high-resolution objective. The light is then split into two paths using a polarizing beam splitter. One of the beams passes through a variable 1:1 telescope before both paths are recombined on a second polarizing beam splitter with a small spatial offset. This enables us to image both planes in a single exposure, with each plane in focus on a separate fixed position of our camera. We calibrated the relative position on the camera of the two imaged planes using 300 shots of a spin-split Mott insulator and the matching algorithm described in the supplement of ref. 20. The overall detection fidelity per atom was 96(1)%.
Potential shaping
The ladder systems are created by superimposing the optical lattice with a repulsive potential, which is shaped by projecting incoherent light at 650 nm (generated from a SLED by Exalos EXS210030-03) from a digital micromirror device (DMD) through the high-resolution objective. Four ladders are created by blocking lattice sites with a potential V = 3.5(5)U around each ladder. The area outside the walled ladders is lifted above the inner ladder potential, but remains below the interaction energy U. It thus serves as a reservoir for surplus atoms, which occupy this region once the lowest Hubbard band of the ladders is filled. The flatness of the potential is adjusted for each parameter setting, as the intensity of the lattice beams directly influence the curvature of the potential. This is accomplished by realizing a system with about 20% doping and returning the average density of 100–150 experimental runs as feedback to the DMD pattern. We repeat the feedback until we reach a sufficiently flat density profile with a variance <1 × 10−3 over the 8L ladder sites. To adjust for drifts in the lattice phase, we continuously track the lattice phase of each experimental run and feedback to the potential position accordingly. In Extended Data Fig. 1, the average density and occupation histograms of all four ladders and the reservoir area are shown for the dataset of L = 7.
Data selection
In each experimental run, four ladder systems are realized. To fulfil the criteria of the Heisenberg regime, we then select on ladder instances with atom number N = 2L and restrict the total magnetization to \({M}^{z}\) = 0, \(|{M}^{z}|=1\), or \(|{M}^{z}|\le 1\), depending on the observable, and specify the magnetization sector whenever data points are presented. \(|{M}^{z}|\le 1\) for 87.5% of all data. Additionally, for all measurements in the Heisenberg regime, we remove ladders with more than two doublons, as those indicate a mismatch of the DMD pattern relative to the lattice phase. To give a specific example, we here give the precise numbers for the data presented in Fig. 2. This dataset consists of 7,032 realizations with four ladders each. Out of those 28,128 ladders, 6,721 have an atom number of 14. In addition, 2,636 ladders then have a total magnetization \({m}^{z}\) = 0 and 3,094 have a magnetization of \({M}^{z}\) = ± 1. Finally 77 of those 2,636 ladders have more than two doublon–hole pairs, which we exclude as these are most likely to be caused by drifts of the potential pattern given by the DMD. This leaves a total of 2,559 ladders out of the initial 28,128 for calculation of the string correlator.
For calculating the string correlators \({g}_{{S}^{z},{R}^{z}}\) and \({g}_{{\mathbb{1}},{R}^{z}}\) at fixed d, we exclude realizations with an odd atom number in the bulk area (grey area in the cartoon of Fig. 2b), as those would lead to imaginary contributions to the correlators, and we also exclude odd atom numbers at the edge areas (green in the cartoon of Fig. 2b). These cases are mostly due to the finite \(U/{t}_{\parallel }\), which still allows for some particle fluctuations. We keep other particle–hole fluctuations, such as those occurring within the string. These do not alter the observed string correlation relative to the Heisenberg model.
Nearest-neighbour spin correlations
The two-leg ladder systems show strong antiferromagnetic spin correlations in which the dominant orientation depends on the ratio of couplings \({J}_{\perp }/{J}_{\parallel }\) and the strength is measured by \({C}_{x}(d)=4\langle {\hat{S}}_{i,j}^{z}{\hat{S}}_{i,j+d}^{z}\rangle \) and \({C}_{y}=4\left\langle {\hat{S}}_{{\rm{A}},j}^{z}{\hat{S}}_{{\rm{B}},j}^{z}\right\rangle \). For a leg coupling \({J}_{\parallel }\) much higher than the rung coupling \({J}_{\perp }\), the nearest-neighbour spin correlator Cy along the rung almost vanishes, whereas correlations reach Cx(1) = −0.500(6) along the leg direction. For a dominating rung coupling \({J}_{\perp }\), Cy reaches −0.58(1), indicating singlet formation between the two sites of a rung. Extended Data Fig. 2a shows the measured spin correlations along both rung and leg for different values of \({J}_{\perp }/{J}_{\parallel }\). The values match the finite-temperature Heisenberg model for an entropy of S/N = (0.3−0.4) kB per particle obtained from ED.
Theory simulation
In this work, we have used two different numerical methods to obtain theoretical predictions for the experimentally measured observables. The results in the Heisenberg regime were obtained using ED of our spin-1/2 ladders up to sizes of L = 9 (limited by computational resources). For each data point, the system size and geometry in the ED simulation are the same as in the experimental data. The finite-temperature results were obtained by using the full spectrum. We specify the entropy per particle s = S/N, which we find to be approximately independent of coupling parameters in the experimental realizations. The results in the Hubbard regime are calculated using the DMRG ansatz44 based on the TeNPy library (v.0.3.0)45. For all calculations, we conserved the total particle number and the total magnetization. For the phase diagram in Fig. 4d we used the iDMRG technique to obtain the ground state and the values of the string order parameters in the thermodynamic limit. For this, we evaluated the ground state for each parameter and used a maximal MPS bond dimension χ = 1,200. The bond dimension is increased in steps Δχ = 40 and the simulation stopped when the difference in the ground state energy per unit cell E(χ + Δχ) − E(χ) < 10−7. This worked for most parameters except in the vicinity of two decoupled Hubbard chains and at small values of \(U/{t}_{\parallel }\). Nevertheless, in this regime we find that the energy per unit cell is converged up to E(1,200) − E(1,160) < 10−4. For the experimentally accessible regime all calculations fulfil the former bound. To obtain the infinite length value of the string order parameters, we calculated it for different lengths \(d\in \)[200, 400, ..., 1600] to make sure that its final value is converged.
Data availability
The datasets generated and analysed during the current study are available from the corresponding author on reasonable request. Source data are provided with this paper.
Code availability
The code used for the analysis are available from the corresponding author on reasonable request.
References
Haldane, F. D. M. Nonlinear field theory of large-spin Heisenberg antiferromagnets: semiclassically quantized solitons of the one-dimensional easy-axis Néel state. Phys. Rev. Lett. 50, 1153–1156 (1983).
Haldane, F. D. M. Topological quantum matter. Int. Journ. Mod. Phys. B 32, 1830004 (2018).
den Nijs, M. & Rommelse, K. Preroughening transistions in crystal surfaces and valence-bond phases in quantum spin chains. Phys. Rev. B 40, 4709–4734 (1989).
Kennedy, T. & Tasaki, H. Hidden Z2 × Z2 symmetry breaking in Haldane-gap antiferromagnets. Phys. Rev. B 45, 304–307 (1992).
Schuch, N., Pérez-García, D. & Cirac, I. Classifying quantum phases using matrix product states and projected entangled pair states. Phys. Rev. B 84, 165139 (2011).
Pollmann, F., Turner, A. M., Berg, E. & Oshikawa, M. Entanglement spectrum of a topological phase in one dimension. Phys. Rev. B 81, 064439 (2010).
Chen, X., Gu, Z.-C. & Wen, X.-G. Classification of gapped symmetric phases in one-dimensional spin systems. Phys. Rev. B 83, 035107 (2011).
Wen, X.-G. Colloquium: zoo of quantum-topological phases of matter. Rev. Mod. Phys. 89, 041004 (2017).
Senthil, T. Symmetry-protected topological phases of quantum matter. Annu. Rev. Condens. Matter Phys. 6, 299324 (2015).
Renard, J. P. et al. Presumption for a quantum energy gap in the quasi-one-dimensional S = 1 Heisenberg antiferromagnet Ni(C2H8N2)2NO2(ClO4). Europhys. Lett. 3, 945–952 (1987).
Buyers, W. J. L. et al. Experimental evidence for the Haldane gap in a spin-1 nearly isotropic, antiferromagnetic chain. Phys. Rev. Lett. 56, 371–374 (1986).
Hagiwara, M., Katsumata, K., Affleck, I., Halperin, B. I. & Renard, J. P. Observation of S = 1/2 degrees of freedom in an S = 1 linear-chain Heisenberg antiferromagnet. Phys. Rev. Lett. 65, 3181–3184 (1990).
Glarum, S. H., Geschwind, S., Lee, K. M., Kaplan, M. L. & Michel, J. Observation of fractional spin S = 1/2 on open ends of S = 1 linear antiferromagnetic chains: nonmagnetic doping. Phys. Rev. Lett. 67, 1614–1617 (1991).
Bakr, W. S., Gillen, J. I., Peng, A., Fölling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature 462, 74–77 (2009).
Sherson, J. F. et al. Single-atom-resolved fluorescence imaging of an atomic Mott insulator. Nature 467, 68–72 (2010).
Haller, E. et al. Single-atom imaging of fermions in a quantum-gas microscope. Nat. Phys. 11, 738–742 (2015).
Cheuk, L. W. et al. Quantum-gas microscope for fermionic atoms. Phys. Rev. Lett. 114, 193001 (2015).
Parsons, M. F. et al. Site-resolved imaging of fermionic 6Li in an optical lattice. Phys. Rev. Lett. 114, 213002 (2015).
Boll, M. et al. Spin- and density-resolved microscopy of antiferromagnetic correlations in Fermi–Hubbard chains. Science 353, 1257–1260 (2016).
Koepsell, J. et al. Robust bilayer charge pumping for spin- and density-resolved quantum gas microscopy. Phys. Rev. Lett. 125, 010403 (2020).
Endres, M. et al. Observation of correlated particle–hole pairs and string order in low-dimensional Mott insulators. Science 334, 200–203 (2011).
Hilker, T. A. et al. Revealing hidden antiferromagnetic correlations in doped Hubbard chains via string correlators. Science 357, 484–487 (2017).
de Léséleuc, S. et al. Observation of a symmetry-protected topological phase of interacting bosons with Rydberg atoms. Science 365, 775–780 (2019).
Affleck, S., Kennedy, E., Lieb, E. H. & Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 59, 799–802 (1987).
Hida, K. Crossover between the Haldane-gap phase and the dimer phase in the spin-1/2 alternating Heisenberg chain. Phys. Rev. B 45, 2207–2212 (1992).
White, S. R. Equivalence of the antiferromagnetic Heisenberg ladder to a single S = 1 chain. Phys. Rev. B 53, 52–55 (1996).
Mazurenko, A. et al. A cold-atom Fermi–Hubbard antiferromagnet. Nature 545, 462–466 (2017).
Auerbach, A. Interacting Electrons and Quantum Magnetism (Springer Science & Business Media, 1994).
Kim, E. H., Fáth, G., Sólyom, J. & Scalapino, D. J. Phase transitions between topologically distinct gapped phases in isotropic spin ladders. Phys. Rev. B 62, 14965–14974 (2000).
Bonesteel, N. E. Valence bonds and the Lieb–Schultz–Mattis theorem. Phys. Rev. B 40, 8954–8960 (1989).
Pollmann, F. & Turner, A. M. Detection of symmetry-protected topological phases in one dimension. Phys. Rev. B 86, 125441 (2012).
Ogata, M. & Shiba, H. Bethe-ansatz wave function, momentum distribution, and spin correlation in the one-dimensional strongly correlated Hubbard model. Phys. Rev. B 41, 2326–2338 (1990).
Miyashita, S. Effects of edges in S = 1 Heisenberg antiferromagnetic chains. Phys. Rev. B 48, 913–919 (1993).
Anfuso, F. & Rosch, A. Fragility of string orders. Phys. Rev. B 76, 085124 (2007).
Moudgalya, S. & Pollmann, F. Fragility of symmetry-protected topological order on a Hubbard ladder. Phys. Rev. B 91, 155128 (2015).
Verresen, R., Bibo, J. &Pollmann, F. Quotient symmetry protected topological phenomena. Preprint at https://arxiv.org/abs/2102.08967 (2021).
Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
Verresen, R., Moessner, R. & Pollmann, F. One-dimensional symmetry protected topological phases and their transitions. Phys. Rev. B 96, 165124 (2017).
Schulz, H. J. Phase diagrams and correlation exponents for quantum spin chains of arbitrary spin quantum number. Phys. Rev. B 34, 6372–6385 (1986).
Nourse, H. L., McCulloch, I. P., Janani, C. & Powell, B. J. Haldane insulator protected by reflection symmetry in the doped Hubbard model on the three-legged ladder. Phys. Rev. B 94, 214418 (2016).
Szasz, A., Motruk, J., Zaletel, M. P. & Moore, J. E. Chiral spin liquid phase of the triangular lattice Hubbard model: a density matrix renormalization group study. Phys. Rev. X 10, 21042 (2020).
Noack, R. M., White, S. R. & Scalapino, D. J. The doped two-chain Hubbard model. Europhys. Lett. 30, 163–168 (1995).
Omran, A. et al. Microscopic observation of Pauli blocking in degenerate fermionic lattice gases. Phys. Rev. Lett. 115, 263001 (2015).
White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).
Hauschild, J. & Pollmann, F. Efficient numerical simulations with tensor networks: Tensor Network Python (TeNPy). SciPost Phys. Lect. Notes 5, 005 (2018).
Acknowledgements
This work was supported by the Max Planck Society (MPG), the European Union (FET-Flag 817482, PASQUANS), the Max Planck Harvard Research Center for Quantum Optics (MPHQ), the Cluster of Excellence ‘CUI: Advanced Imaging of Matter’ of the Deutsche Forschungsgemeinschaft (DFG) – EXC 2056 – project ID 390715994 and under Germany’s Excellence Strategy – EXC-2111-390814868. J.K. acknowledges funding from Hector Fellow Academy and T.C. from the Alexander v. Humboldt foundation. R.V. is supported by the Harvard Quantum Initiative Postdoctoral Fellowship in Science and Engineering and by the Simons Collaboration on Ultra-Quantum Matter (Simons Foundation, 651440, Ashvin Vishwanath). F.P. acknowledges the support of the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 771537). P.S. acknowledges support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (grant number B05F640051).
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
P.S., S.H. and D.B. planned the experiment and analysed the data. P.S., S.H., D.B., T.C. and P.B. collected the data. T.C. carried out the ED calculations. J.K. and G.S. contributed to the upgrade of the experimental apparatus. J.B., R.V. and F.P. performed the DMRG simulations and analytical calculations. T.A.H., C.G. and I.B. supervised the study. All authors contributed extensively to interpretation of the data and production of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Density engineering.
a, Repulsive light shaped with a DMD splits the system into four independent ladders in the centre surrounded by a low-density bath. The density of the ladders is n = 0.992 with a standard deviation of 0.03. b, The occupation histograms show the normalized occurrence of total atom numbers in each ladder and the normalized occurrence in the surrounding bath for L = 7. Almost 25% of the ladder realizations have N = 2L.
Extended Data Fig. 2 Nearest-neighbour spin correlations.
The nearest-neighbour spin correlation C(1) for different \({J}_{\perp }/{J}_{\parallel }\) in the L = 5 system. The brown (purple) points refer to the correlations along the rung (leg). The shaded areas correspond to the correlations in the Heisenberg model with an entropy of S/N = (0.3−0.4) kB per particle. Both theoretical and experimental values are obtained from the magnetization sector \({m}^{z}\) = 0.
Supplementary information
Supplementary Information
Supplementary text, figures, equations and references.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sompet, P., Hirthe, S., Bourgund, D. et al. Realizing the symmetry-protected Haldane phase in Fermi–Hubbard ladders. Nature 606, 484–488 (2022). https://doi.org/10.1038/s41586-022-04688-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04688-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.