Abstract
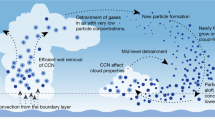
New particle formation in the upper free troposphere is a major global source of cloud condensation nuclei (CCN)1,2,3,4. However, the precursor vapours that drive the process are not well understood. With experiments performed under upper tropospheric conditions in the CERN CLOUD chamber, we show that nitric acid, sulfuric acid and ammonia form particles synergistically, at rates that are orders of magnitude faster than those from any two of the three components. The importance of this mechanism depends on the availability of ammonia, which was previously thought to be efficiently scavenged by cloud droplets during convection. However, surprisingly high concentrations of ammonia and ammonium nitrate have recently been observed in the upper troposphere over the Asian monsoon region5,6. Once particles have formed, co-condensation of ammonia and abundant nitric acid alone is sufficient to drive rapid growth to CCN sizes with only trace sulfate. Moreover, our measurements show that these CCN are also highly efficient ice nucleating particles—comparable to desert dust. Our model simulations confirm that ammonia is efficiently convected aloft during the Asian monsoon, driving rapid, multi-acid HNO3–H2SO4–NH3 nucleation in the upper troposphere and producing ice nucleating particles that spread across the mid-latitude Northern Hemisphere.
Similar content being viewed by others
Main
Intense particle formation has been observed by airborne measurements as a persistent, global-scale band in the upper troposphere over tropical convective regions1,2,4. Upper tropospheric nucleation is thought to provide at least one-third of global CCN3. Increased aerosols since the industrial revolution, and their interactions with clouds, have masked a large fraction of the global radiative forcing by greenhouse gases. Projections of aerosol radiative forcing resulting from future reductions of air pollution are highly uncertain7. Present-day nucleation involves sulfuric acid (H2SO4) over almost all the troposphere8. However, binary nucleation of H2SO4–H2O is slow and, so, ternary or multicomponent nucleation with extra vapours such as ammonia (NH3)9 and organics10,11 is necessary to account for observed new-particle-formation rates3,8,12.
Ammonia stabilizes acid–base nucleation and strongly enhances particle formation rates9. However, ammonia is thought to be extremely scarce in the upper troposphere because its solubility in water and reactivity with acids should lead to efficient removal in convective clouds. However, this assumption is not supported by observation. Ammonia vapour has been repeatedly detected in the Asian monsoon upper troposphere, with mixing ratios of up to 30 pptv (2.5 × 108 cm−3) for a three-month average5 and up to 1.4 ppbv (1.2 × 1010 cm−3) in hotspots6. The release of dissolved ammonia from cloud droplets may occur during glaciation13. Once released in the upper troposphere, ammonia can form particles with nitric acid, which is abundantly produced by lightning14,15. These particles will live longer and travel farther than ammonia vapour, with the potential to influence the entire upper troposphere and lower stratosphere of the Northern Hemisphere6.
Fundamental questions remain about the role and mechanisms of nitric acid and ammonia in upper tropospheric particle formation. Recent CLOUD (Cosmics Leaving Outdoor Droplets) experiments at CERN have shown that nitric acid and ammonia vapours below 278 K can condense onto newly formed particles as small as a few nanometres in diameter, driving rapid growth to CCN sizes16. At even lower temperatures (below 258 K), nitric acid and ammonia can directly nucleate to form ammonium nitrate particles, although pure HNO3–NH3 nucleation is too slow to compete with H2SO4–NH3 nucleation under comparable conditions. However, the results we present here show that, when all three vapours are present, a synergistic interaction drives nucleation rates orders of magnitude faster than those from any two of the three components. Once nucleated through this multi-acid–ammonia mechanism, the particles can grow rapidly by co-condensation of NH3 and HNO3 alone, both of which may be far more abundant than H2SO4 in the upper troposphere.
Particle formation measurements in CLOUD
Here we report new-particle-formation experiments performed with mixtures of sulfuric acid, nitric acid and ammonia vapours in the CLOUD chamber9 at CERN between September and December 2019 (CLOUD 14; see Methods for experimental details). To span ranges typical of the upper troposphere, we established quasi-steady-state vapour concentrations in the chamber of (0.26–4.6) × 106 cm−3 sulfuric acid (through photochemical oxidation of SO2), (0.23–4.0) × 109 cm−3 nitric acid (through either photochemical oxidation of NO2 or injection from an evaporator) and (0.95–6.5) × 108 cm−3 ammonia (through injection from a gas bottle). In an extreme experiment to simulate hotspot conditions in the Asian monsoon anticyclone, we raised sulfuric acid, nitric acid and ammonia to maximum concentrations of 6.2 × 107 cm−3, 3.8 × 109 cm−3 and 8.8 × 109 cm−3, respectively. The experiments were conducted at 223 K and 25% relative humidity, representative of upper tropospheric conditions.
Figure 1 shows the evolution of a representative new-particle-formation experiment in the presence of around 6.5 × 108 cm−3 ammonia. The top three panels show particle number concentrations above 1.7 nm and above 2.5 nm (Fig. 1a), particle formation rate at 1.7 nm (J1.7) (Fig. 1b) and particle size distribution (Fig. 1c). The bottom panel shows HNO3 and H2SO4 vapour concentrations (Fig. 1d). We switched on the ultraviolet (UV) lights at t = 0 min to oxidize SO2 with OH radicals and form H2SO4. Sulfuric acid started to appear shortly thereafter and built up to a steady state of 2.3 × 106 cm−3 over the wall-loss timescale of about 10 min. Under these conditions, the data show a modest formation rate of 1.7-nm particles from H2SO4–NH3 nucleation, consistent with previous CLOUD measurements8. These particles grew only slowly (about 0.5 nm h−1 at this H2SO4 and particle size17). No particles reached 2.5 nm within 2 h, owing to their slow growth rate and low survival probability against wall loss.
a, Particle number concentrations versus time at mobility diameters >1.7 nm (magenta) and >2.5 nm (green). The solid magenta trace is measured by a PSM1.7 and the solid green trace is measured by a CPC2.5. The fixed experimental conditions are about 6.5 × 108 cm−3 NH3, 223 K and 25% relative humidity. A microphysical model reproduces the main features of the observed particle formation (dashed lines; see text for details). b, Particle formation rate versus time at 1.7 nm (J1.7), measured by a PSM. c, Particle size distribution versus time, measured by an SMPS. d, Gas-phase nitric acid and sulfuric acid versus time, measured by an I− CIMS and a NO3− CIMS, respectively. Sulfuric acid through SO2 oxidation started to appear soon after switching on the UV lights at time = 0 min, building up to a steady state of 2.3 × 106 cm−3 after a wall-loss-rate timescale of around 10 min. The subsequent H2SO4–NH3 nucleation led to a relatively slow formation rate of 1.7-nm particles. The particles did not grow above 2.5 nm because of their slow growth rate and corresponding low survival probability against wall loss. Following injection of 2.0 × 109 cm−3 nitric acid into the chamber after 115 min, while leaving the production rate of sulfuric acid and the injection rate of ammonia unchanged, we observed a sharp increase in particle formation rate (panel b), together with rapid particle growth of 40 nm h−1 (panel c). The overall systematic scale uncertainties of ±30% on particle formation rate, −33%/+50% on sulfuric acid concentration and ±25% on nitric acid concentration are not shown.
At t = 115 min, we raised the nitric acid concentration to 2.0 × 109 cm−3, through direct injection instead of photochemical production, so that we could independently control the nitric acid and sulfuric acid concentrations. The particle number increased 30-fold and 1,300-fold for particles larger than 1.7 nm and 2.5 nm, respectively. In addition, these newly formed particles grew much more rapidly (40 nm h−1), reaching 20 nm within 30 min. This experiment shows that nitric acid can substantially enhance particle formation and growth rates for fixed levels of sulfuric acid and ammonia.
We also conducted model calculations on the basis of known thermodynamics and microphysics (Methods). Our model results (dashed traces in Fig. 1a) consistently and quantitatively confirm the experimental data: sulfuric acid and ammonia nucleation produces only 1.7-nm particles, whereas addition of nitric acid strongly enhances the formation rates of both 1.7-nm and 2.5-nm particles.
We conducted two further experiments under conditions similar to Fig. 1 but holding the concentrations of a different pair of vapours constant while varying the third. For the experiment shown in Extended Data Fig. 1, we started by oxidizing NO2 to produce 1.6 × 109 cm−3 HNO3 in the presence of about 6.5 × 108 cm−3 NH3 and then increased H2SO4 from 0 to 4.9 × 106 cm−3 by oxidizing progressively more injected SO2. For the experiment shown in Extended Data Fig. 2, we first established 4.6 × 106 cm−3 H2SO4 and 4.0 × 109 cm−3 HNO3, and then increased NH3 from 0 to about 6.5 × 108 cm−3. We consistently observed relatively slow nucleation when only two of the three vapours are present, whereas addition of the third vapour increased nucleation rates by several orders of magnitude.
Figure 2 shows particle formation rates measured by CLOUD at 1.7-nm mobility diameter (J1.7) versus ammonia concentration, at 223 K. The J1.7 data were all measured in the presence of ions from galactic cosmic rays (GCR) and — so — represent the sum of neutral and ion-induced channels. The black diamond shows the measured J1.7 of 0.3 cm−3 s−1 for HNO3–NH3 nucleation with 1.5 × 109 cm−3 nitric acid, about 6.5 × 108 cm−3 ammonia and sulfuric acid below the detection limit of 5 × 104 cm−3 (this is the event shown in Extended Data Fig. 1). At this same ammonia concentration, we measured J1.7 = 6.1 cm−3 s−1 at 2.3 × 106 cm−3 H2SO4, demonstrating the much faster rate of H2SO4–NH3 nucleation (not shown). This measurement is consistent with models on the basis of previous CLOUD studies of H2SO4–NH3 nucleation18,19, as illustrated by the model simulations for 4.0 × 106 cm−3 sulfuric acid (red solid curve). The blue circles show our measurements of J1.7 for HNO3–H2SO4–NH3 nucleation at 4.0 × 106 cm−3 sulfuric acid and (1.6–6.5) × 108 cm−3 ammonia, in the presence of 1.5 × 109 cm−3 nitric acid (the event shown in Extended Data Fig. 2). The blue dashed curve is a power law fit to the measurements, indicating a strong sensitivity to ammonia concentration \((\,{J}_{1.7}=k{[{{\rm{NH}}}_{3}]}^{3.7})\).
The chemical systems are HNO3–NH3 (black), H2SO4–NH3 (red) and HNO3–H2SO4–NH3 (blue). The black diamond shows the CLOUD measurement of HNO3–NH3 nucleation at 1.5 × 109 cm−3 HNO3, 6.5 × 108 cm−3 NH3 and with H2SO4 below the detection limit of 5 × 104 cm−3. The red solid curve is J1.7 versus ammonia concentration at 4.0 × 106 cm−3 sulfuric acid from a H2SO4–NH3 nucleation parameterization on the basis of previous CLOUD measurements18,19. The blue circles show the CLOUD measurements of HNO3–H2SO4–NH3 nucleation at 4.0 × 106 cm−3 H2SO4, 1.5 × 109 cm−3 HNO3 and (1.6–6.5) × 108 cm−3 NH3. The data are fitted by a power law, J1.7 = k[NH3]3.7 (blue dashed curve). The vertical grey dotted line separates ammonia concentrations measured in different regions in the upper troposphere5; the region to the right indicates the Asian monsoon conditions. The horizontal grey solid lines show J1.7 upper limits for ion-induced nucleation resulting from the GCR ionization rate of around 2 ion pairs cm−3 s−1 at ground level and 35 ion pairs cm−3 s−1 in the upper troposphere. Among the three nucleation mechanisms, H2SO4–NH3 nucleation dominates in regions with low ammonia (below around 1.0 × 108 cm−3, or 12 pptv), whereas HNO3–H2SO4–NH3 nucleation dominates at higher ammonia levels characteristic of the Asian monsoon upper troposphere. The bars indicate 30% estimated total error on the particle formation rates. The overall systematic scale uncertainties are −33%/+50% for sulfuric acid and ±25% for nitric acid concentrations.
The vertical grey dotted line in Fig. 2 separates ammonia concentrations measured in different regions in the upper troposphere5; Asian monsoon conditions are to the right of this vertical line. Our results indicate that H2SO4–NH3 nucleation is probably responsible for new particle formation in regions with ammonia concentrations below around 108 cm−3 (12 pptv), but that HNO3–H2SO4–NH3 nucleation probably dominates at higher ammonia levels in the Asian monsoon upper troposphere. Our nucleation rate measurements confirm that the stronger sulfuric acid is favoured by ammonia in the ammonia-limited regime, so nitric acid will evaporate from the clusters, as it may be displaced by sulfuric acid. However, as ammonia increases from 1.6 to 6.5 × 108 cm−3, we observe sharp increases in J1.7 for HNO3–H2SO4–NH3 nucleation from 10 to 400 cm−3 s−1 and in the ratio of particle formation rates (HNO3–H2SO4–NH3:H2SO4–NH3) from 4 to 30. Our nucleation model (as in Fig. 1) yields slightly higher J1.7 than that observed, as shown in Extended Data Fig. 3, but the formation rate variation with ammonia, nonetheless, shows a similar slope.
CLOUD has previously shown that ions enhance nucleation for all but the strongest acid–base clusters; HNO3–H2SO4–NH3 is probably not an exception. However, the ion enhancement is limited by the GCR ion-pair production rate. We show with the horizontal grey solid lines in Fig. 2 the upper limits on J1.7 for ion-induced nucleation of about 2 cm−3 s−1 at ground level and 35 cm−3 s−1 in the upper troposphere. Our experimental nucleation rates for HNO3–H2SO4–NH3 are mostly above upper tropospheric GCR ion production rates. This is confirmed by similar J1.7 measured during a neutral nucleation experiment, in which an electric field was used to rapidly sweep ions from the chamber. Thus, for this nucleation scheme, the neutral channel will often prevail over the ion-induced channel in the Asian monsoon upper troposphere. However, when ammonia is diluted away outside the Asian monsoon anticyclone, ions may enhance the nucleation rate up to the GCR limit near 35 cm−3 s−1.
In a formal sense, the new-particle-formation mechanism could be one of two types: formation of stable H2SO4–NH3 clusters, followed by nano-Köhler-type activation by nitric acid and ammonia16; or else true synergistic nucleation of nitric acid, sulfuric acid and ammonia9. In a practical sense, it makes little difference because coagulation loss is a major sink for all small clusters in the atmosphere20, so appearance of 1.7-nm particles by means of any mechanism constitutes new particle formation. Regardless, we can distinguish between these two possibilities from our measurements of the molecular composition of negatively charged clusters using an atmospheric pressure interface time-of-flight (APi-TOF) mass spectrometer. In Fig. 3, we show cluster mass defect plots during H2SO4–NH3 and HNO3–H2SO4–NH3 nucleation events at 223 K. The marked difference between Fig. 3a, b indicates that nitric acid changes the composition of the nucleating clusters down to the smallest sizes; thus, the mechanism is almost certainly synergistic HNO3–H2SO4–NH3 nucleation.
Mass defect (difference from integer mass) versus mass/charge (m/z) of negatively charged clusters measured with an APi-TOF mass spectrometer for 1.7 × 106 cm−3 sulfuric acid and 6.5 × 108 cm−3 ammonia (a) and 2.0 × 107 cm−3 sulfuric acid, 3.2 × 109 cm−3 nitric acid and 7.9 × 109 cm−3 ammonia (b). The symbol colours indicate the molecular composition as shown. The symbol area is proportional to the logarithm of signal rate (counts per second). The labels (m:n) near the symbols indicate the number of sulfuric acid (H2SO4)m and ammonia (NH3)n molecules in the clusters, including both neutral and charged species. The grey dashed lines follow clusters that contain pure H2SO4 molecules with an HSO4− ion (or SO4 instead of H2SO4 and/or SO4− instead of HSO4− for pure H2SO4 clusters falling below this line in b). The grey solid lines follow the 1:1 H2SO4–NH3 addition starting at (H2SO4)4–(NH3)0. Nearly all clusters in panel a lie above this line, whereas nearly all clusters in panel b fall below it. Most clusters containing HNO3 lack NH3 by the time they are measured (they fall near the (m:0) grey dashed line), but the marked difference between a and b indicates that the nucleating clusters had distinctly different compositions, probably including relatively weakly bound HNO3–NH3 pairs in b. It is probable that nucleating clusters in the CLOUD chamber at 223 K contain HNO3–H2SO4–NH3 with a roughly 1:1 acid–base ratio. However, during the transmission from the chamber to the warm APi-TOF mass spectrometer at 293 K, the clusters lose HNO3 and NH3, leaving a less volatile core of H2SO4 with depleted NH3. The evaporation of a single NH3 or HNO3 molecule from a cluster displaces it on the mass defect plot by a vector distance indicated by the black arrows in b.
In Fig. 3a, the predominant ions are one of several deprotonated sulfuric acid species, including HSO4−, SO4−, HSO5−, SO5− and so on, resulting in a group of points for clusters with similar molecular composition but different mass and mass defect. In the figure, we use the labels (m:n) to indicate the number of sulfuric acid and ammonia molecules in the (H2SO4)m–(NH3)n clusters, including both neutral and charged species. The mass defect plot closely resembles those previously measured for H2SO4–NH3 nucleation21. Negative-ion-induced nucleation proceeds with the known acid–base stabilization mechanism, in which sulfuric acid dimers form as a first step (with HSO4− serving as a conjugate base for the first H2SO4) and then clusters subsequently grow by 1:1 H2SO4–NH3 addition (that is, as ammonium bisulfate)9. We use a grey line to illustrate the 1:1 addition path, beginning at (H2SO4)4–(NH3)0. Clusters larger than the sulfuric acid tetramers mostly contain several ammonia molecules and, so nearly all clusters in Fig. 3a lie above the grey line.
Figure 3b shows a pronounced change in the cluster APi-TOF signal during HNO3–H2SO4–NH3 nucleation. In addition to pure (H2SO4)m–(NH3)n clusters, we observe clusters with one extra HNO3 molecule (or NO3− ion), that is, (HNO3)1–(H2SO4)m–(NH3)n, and the pure nitric acid monomer and dimer. In sharp contrast with Fig. 3a, all these clusters are deficient in NH3, falling below the same grey line as in Fig. 3a. The most deficient contain up to nine bare acids, that is, (H2SO4)9 or (H2SO4)8–(HNO3)1. Figure 3b almost certainly does not represent the true cluster composition in the chamber because binary nucleation of H2SO4 does not proceed under these exact conditions of H2SO4, NH3, temperature and relative humidity (as demonstrated by Fig. 3a). We can interpret Fig. 3b as follows. It is probable that clusters in the CLOUD chamber (223 K) contain HNO3–H2SO4–NH3 with a roughly 1:1 acid–base ratio, representing partial neutralization. However, during the transmission from the cold chamber to the warm APi-TOF mass spectrometer (about 293 K), the clusters lose relatively weakly bound HNO3 and NH3 molecules but not the lower-volatility H2SO4 molecules. Regardless of the interpretation, however, the notable difference between Fig. 3a, b indicates that the sampled clusters had very different compositions and that nitric acid participated in the formation of clusters as small as a few molecules.
Ice nucleation measurements
Nitric acid and ammonia not only enhance the formation rate of new particles but also drive their rapid growth to sizes at which they may act as CCN or ice nucleating particles (INP), above around 50 nm. To assess their effect on cirrus clouds, we measured the ice nucleation ability of particles formed from HNO3–H2SO4–NH3 nucleation in the CLOUD chamber. Simulating ‘hotspot’ conditions, we first formed pure ammonium nitrate particles by means of HNO3–NH3 nucleation and then increased the H2SO4 fraction in the particles by oxidizing progressively more SO2. We measured their ice nucleation ability using the online continuous flow diffusion instrument, mINKA (Methods and Extended Data Fig. 4). As shown in Fig. 4a, pure ammonium nitrate particles (purple data points) nucleate ice only at high ice saturation ratios (Sice), characteristic of homogeneous nucleation (shown by a steep increase of ice activation above Sice = 1.60 at 215 K). This indicates that pure ammonium nitrate particles, formed by means of HNO3–NH3 nucleation, are probably in a liquid state initially, albeit at a relative humidity below the deliquescence point22. However, addition of sulfate, with a particulate sulfate-to-nitrate molar ratio as small as 10−4, triggers crystallization of ammonium nitrate. For these particles, we observed a small heterogeneous ice nucleation mode at Sice of 1.54 (blue data points), with other conditions and the particle size distribution held almost constant. Moreover, as the sulfate molar fraction progressively rises to just 0.017 (still almost pure but now solid ammonium nitrate), an active surface site density (ns) of 1010 m−2 is reached at Sice as low as 1.26. This is consistent with previous findings, in which particles were generated through nebulization, with a much larger particle diameter and a much higher sulfate-to-nitrate ratio23. Our measurements show that HNO3–H2SO4–NH3 nucleation followed by rapid growth from nitric acid and ammonia condensation — which results in low sulfate-to-nitrate ratio — could provide an important source of INP that are comparable with typical desert dust particles at nucleating ice24.
a, Active surface site density versus ice saturation ratio, measured by the mINKA instrument at CLOUD, at 233 K and 25% relative humidity. Pure ammonium nitrate particles (purple points) show homogeneous freezing. However, addition of only small amounts of sulfate creates highly ice-nucleation-active particles. At around 1.7% sulfate fraction (red points), the ice nucleating efficiency is comparable with desert dust particles24. b, Simulation of particle formation in a global model (EMAC) with efficient vertical transport of ammonia into the upper troposphere during the Asian monsoon. Including multi-acid HNO3–H2SO4–NH3 nucleation (on the basis of the blue dashed curve in Fig. 2) enhances particle number concentrations (nucleation mode) over the Asian monsoon region by a factor of 3–5 compared with the same model with only H2SO4–NH3 nucleation (from Dunne et al.8, similar to the red solid curve in Fig. 2).
Atmospheric implications
Our findings suggest that HNO3–H2SO4–NH3 nucleation may dominate new particle formation in the Asian monsoon region of the upper troposphere, with a ‘flame’ of new particles in the outflow of convective clouds, in which up to 1010 cm−3 ammonia6 mixes with low (background) levels of sulfuric acid and nitric acid. Without this mechanism, particle formation through the traditional ternary H2SO4–NH3 nucleation would be much slower and most probably rate-limited by the scarce sulfuric acid. Furthermore, by co-condensing with nitric acid, the convected ammonia also drives the growth of the newly formed particles. Given typical acid-excess conditions in the upper troposphere, condensational growth is governed by the availability of ammonia. Consequently, particles will steadily (and rapidly) grow until ammonia is depleted after several e-folding times set by the particle condensation sink. On the basis of condensation sinks generally observed in the tropical upper troposphere4, this timescale will be several hours. Within this time interval, given the observed ammonia levels, newly formed particles will be able to grow to CCN sizes and even small admixtures of sulfuric acid will render these particles efficient INP.
Our laboratory measurements provide a mechanism that can account for recent observations of abundant ammonium nitrate particles in the Asian monsoon upper troposphere6. To evaluate its importance on a global scale, we first parameterized our experimentally measured J1.7 for HNO3–H2SO4–NH3 nucleation as a function of sulfuric acid, nitric acid and ammonia concentrations (Methods). The parameterization is obtained using a power-law dependency for each vapour (Extended Data Fig. 5), given that the critical cluster composition is associated with the exponents according to the first nucleation theorem25. Then we implemented this parameterization in a global aerosol model (EMAC, see Methods for modelling details). The EMAC model predicts that HNO3–H2SO4–NH3 nucleation at 250 hPa (11 km, approximately 223 K) produces an annual average exceeding 1,000 cm−3 new particles over an extensive area (Extended Data Fig. 6). This corresponds to an increase in particle number concentration (Fig. 4b) up to a factor of five higher than in a control simulation with only ternary H2SO4–NH3 nucleation8. The strongest increase occurs mostly over Asia, in which ammonia is ample because of deep convection from ground sources.
However, another global model (TOMCAT, see Methods) shows much lower ammonia mixing ratios in the upper troposphere than EMAC (<1 pptv compared with <100 pptv, respectively), although with a broadly similar spatial distribution (Extended Data Fig. 7a, b). This large variability of upper tropospheric ammonia is also indicated by recent field measurements on local6,26 and global5,27 scales. In view of its importance for both H2SO4–NH3 and HNO3–H2SO4–NH3 nucleation, there is an urgent need to improve upper tropospheric measurements of ammonia, as well as improve knowledge of its sources, transport and sinks.
We thus turned to a cloud-resolving model to estimate the ammonia vapour fraction remaining after deep convection (see Methods). We show in Extended Data Fig. 8 that around 10% of the boundary layer ammonia can be transported into the upper troposphere and released as vapour by a base-case convective cloud. The sensitivity tests further illustrate that the key factor governing the fraction of ammonia remaining in the cloud outflow is the retention of ammonia molecules by ice particles (Extended Data Fig. 8e), whereas cloud water pH (Extended Data Fig. 8c) and cloud water content (Extended Data Fig. 8d) only play minor roles once glaciation occurs. Given that more than 10 ppbv of ammonia is often observed in the Asian boundary layer28, it is plausible that the observed 1.4 ppbv (1010 cm−3) ammonia in the upper troposphere6 is indeed efficiently transported by the convective systems.
Although the ammonium–nitrate–sulfate particles are formed locally, they can travel from Asia to North America in just three days by means of the subtropical jet stream, as the typical residence time of Aitken mode particles ranges from one week to one month in the upper troposphere29. As a result, these particles can persist as an intercontinental band, covering more than half of the mid-latitude surface area of the Northern Hemisphere (Extended Data Fig. 6). In summary, synergistic nucleation of nitric acid, sulfuric acid and ammonia could provide an important source of new CCN and ice nuclei in the upper troposphere, especially over the Asian monsoon region, and is closely linked with anthropogenic ammonia emissions27.
Methods
The CLOUD facility
We conducted our measurements at the CERN CLOUD facility, a 26.1-m3, electropolished, stainless-steel CLOUD chamber that allows new-particle-formation experiments under the full range of tropospheric conditions with scrupulous cleanliness and minimal contamination9,30. The CLOUD chamber is mounted in a thermal housing, capable of keeping the temperature constant in the range 208 K and 373 K with a precision of ±0.1 K (ref. 31). Photochemical processes are initiated by homogeneous illumination with a built-in UV fibre-optic system, including four 200-W Hamamatsu Hg-Xe lamps at wavelengths between 250 and 450 nm and a 4-W KrF excimer UV laser at 248 nm with adjustable power. New particle formation under different ionization levels is simulated with and without the electric fields (±30 kV), which can artificially scavenge or preserve small ions produced from ground-level GCR. Uniform spatial mixing is achieved with magnetically coupled stainless-steel fans mounted at the top and bottom of the chamber. The characteristic gas mixing time in the chamber during experiments is a few minutes. The loss rate of condensable vapours and particles onto the chamber walls is comparable with the ambient condensation sink. To avoid contamination, the chamber is periodically cleaned by rinsing the walls with ultra-pure water and heating to 373 K for at least 24 h, ensuring extremely low contaminant levels of sulfuric acid <5 × 104 cm−3 and total organics <50 pptv (refs. 32,33). The CLOUD gas system is also built to the highest technical standards of cleanliness and performance. The dry air supply for the chamber is provided by boil-off oxygen (Messer, 99.999%) and boil-off nitrogen (Messer, 99.999%) mixed at the atmospheric ratio of 79:21. Highly pure water vapour, ozone and other trace gases such as nitric acid and ammonia can be precisely added at the pptv level from ultra-pure sources.
Instrumentation
Gas-phase sulfuric acid was measured using a nitrate chemical ionization APi-TOF (nitrate-CI-APi-TOF) mass spectrometer34,35 and an iodide chemical ionization time-of-flight mass spectrometer equipped with a Filter Inlet for Gases and Aerosols (I-FIGAERO-CIMS)36,37. The nitrate-CI-APi-TOF mass spectrometer is equipped with an electrostatic filter in front of the inlet to remove ions and charged clusters formed in the chamber. A corona charger is used to ionize the reagent nitric acid vapour in a nitrogen flow38. Nitrate ions are then guided in an atmospheric pressure drift tube by an electric field to react with the analyte molecules in the sample flow. Sulfuric acid is quantified for the nitrate-CI-APi-TOF with a detection limit of about 5 × 104 cm−3, following the same calibration and loss correction procedures described previously9,32,39. FIGAERO is a manifold inlet for a CIMS with two operating modes. In the sampling mode, a coaxial core sampling is used to minimize the vapour wall loss in the sampling line. The total flow is maintained at 18.0 slpm and the core flow at 4.5 slpm; the CIMS samples at the centre of the core flow with a flow rate of 1.6 slpm. Analyte molecules are introduced into a 150-mbar ion-molecule reactor, chemically ionized by iodide ions that are formed in a Po-210 radioactive source and extracted into the mass spectrometer. The sulfuric acid calibration coefficient for the I-FIGAERO-CIMS is derived using the absolute sulfuric acid concentrations measured with the pre-calibrated nitrate-CI-APi-TOF.
Gas-phase nitric acid was also measured using the I-FIGAERO-CIMS. Nitric acid concentration was quantified by measuring HNO3/N2 mixtures with known nitric acid concentrations, following similar procedures described previously16. The HNO3/N2 mixture was sourced from flowing 2 slpm ultra-pure nitrogen through a portable nitric acid permeation tube, at constant 40 °C. The permeation rate of nitric acid was determined by passing the outflow of the permeation tube through an impinger containing deionized water and analysing the resulting nitric acid solution through spectrophotometry.
Gas-phase ammonia was either measured or calculated. We measured ammonia using a proton transfer reaction time-of-flight mass spectrometer (PTR3-TOF-MS, or PTR3 for short)40. As a carrier gas for the primary ions, we used argon (ultra-high purity 5.0) to ensure that ammonium ions could not be artificially formed in the region of the corona discharge. Although the theoretical detection limit from peak height and width would be even smaller, the lowest concentration we were able to measure during the first fully ammonia-free runs of the beginning of the campaign was 109 cm−3. An explanation for this is that, when concentrations of ammonia are low, effects of wall interaction of the highly soluble ammonia become important and the decay of ammonia in the inlet line becomes very slow. To reduce inlet wall contacts, we used a core-sampling technique directly in front of the instrument to sample only the centre 2 slpm of the 10 slpm inlet flow, but owing to frequent necessary on-site calibrations of volatile organic compounds, a Teflon ball valve was placed within the sample line that probably influenced measurements during times of low ammonia concentrations. At concentrations above about 2 × 109 cm−3 ammonia, however, the response of the instrument was very fast, so that, for example, changes in the chamber ammonia flow rate were easily detectable. Off-site calibrations showed a humidity-independent calibration factor of 0.0017 ncps/ppb. Calibrated data from the PTR3 agree very well with the Picarro above 1010 cm−3 (detection limit of the Picarro). The PTR3 also provides information about the overall cleanliness of the volatile organic compounds in the chamber. The technique was extensively described previously40.
For ammonia concentrations below 109 cm−3, we calculated concentration using the calibrated ammonia injection flow and an estimated first-order wall-loss rate. The wall-loss rate (kwall) for ammonia inside the CLOUD chamber is confirmed to be faster than for sulfuric acid41, and can be determined from the following expression42:
in which A/V is the surface-to-volume ratio of the chamber, ke is the eddy diffusion constant (determined by the turbulent mixing intensity, not the transport properties of the gases) and Di is the diffusion coefficient for each gas. Cwall is thus referred to as an empirical parameter of experiment conditions in the chamber. Here we first determine the kwall for sulfuric acid and nitric acid to be 1.7 × 10−3 and 1.9 × 10−3 s−3, respectively, by measuring their passive decay rates and subtracting the loss rate of chamber dilution for both (1.2 × 10−3 s−1), as well as the loss rate of dimer formation for sulfuric acid (around 1.6 × 10−3 s−1 for 5 × 106 cm−3 H2SO4). The kwall for sulfuric acid agrees with our measurements from previous campaigns43. We then derive the Cwall for sulfuric acid and nitric acid both to be 2.0 × 10−4 torr−0.5 cm−1 s−0.5, with \({D}_{{{\rm{H}}}_{2}{{\rm{SO}}}_{4}}\) of 74 torr cm2 s−1 and \({D}_{{{\rm{HNO}}}_{3}}\) of 87 torr cm2 s−1 (ref. 44). Finally, we calculate the kwall for ammonia to be 2.7 × 10−3 s−1, with \({D}_{{{\rm{NH}}}_{3}}\) of 176 torr cm2 s−1 (ref. 44). Ammonia desorption from the chamber surface is a strong function of the temperature and is believed to be negligible at low temperatures30. Even after a long time exposure, ammonia desorption should be less than 1.6 × 106 cm−3, according to previous parameterization of ammonia background contamination in the CLOUD chamber41.
The composition of negatively charged ions and clusters were determined using an APi-TOF mass spectrometer45. The APi-TOF mass spectrometer is connected to the CLOUD chamber by means of a 1-inch (21.7-mm inner diameter) sampling probe, with coaxial core sampling to minimize the wall losses in the sampling line. The total sample flow is maintained at 20 slpm and the core sample flow for the APi-TOF mass spectrometer at 0.8 slpm. Because this instrument only measures charged clusters, the measurements were made during GCR conditions. Owing to a large temperature difference between the cold chamber (223 K) and the warm APi-TOF mass spectrometer (around 293 K), HNO3–H2SO4–NH3 clusters probably lose relatively weakly bonded HNO3 and NH3 molecules. This resembles the chemical ionization process of detecting ammonia with the nitrate-CI-APi-TOF, in which HNO3 and NH3 molecules rapidly evaporate from the resulting ammonia nitrate cluster in the CI-APi-TOF vacuum regions46.
Gas monitors were used to measure ozone (O3, Thermo Environmental Instruments TEI 49C), sulfur dioxide (SO2, Thermo Fisher Scientific Inc. 42i-TLE) and nitric oxide (NO, ECO Physics, CLD 780TR). Nitrogen dioxide (NO2) was measured by a cavity attenuated phase shift nitrogen dioxide monitor (CAPS NO2, Aerodyne Research Inc.) and a home-made cavity enhanced differential optical absorption spectroscopy (CE-DOAS) instrument. The relative humidity of the chamber was determined by dew point mirrors (EdgeTech).
Particle number concentrations were monitored by condensation particle counters (CPCs), including an Airmodus A11 nano Condensation Nucleus Counter (nCNC), consisting of a particle size magnifier (PSM) and a laminar-flow butanol-based CPC47, as well as a butanol TSI 3776 CPC. Particle size distributions between 1.8 nm and 500 nm were measured by a nano-scanning electrical mobility spectrometer (nSEMS), a nano-scanning mobility particle sizer (nano-SMPS) and a long-SMPS. The nSEMS used a new, radial opposed migration ion and aerosol classifier (ROMIAC), which is less sensitive to diffusional resolution degradation than the DMAs48, and a soft X-ray charge conditioner. After leaving the classifier, particles were first activated in a fast-mixing diethylene glycol stage49 and then counted with a butanol-based CPC. The nSEMS transfer function that was used to invert the data to obtain the particle size distribution was derived using 3D finite element modelling of the flows, electric field and particle trajectories50,51. The two commercial mobility particle size spectrometers, nano-SMPS and long-SMPS, have been fully characterized, calibrated and validated in several previous studies52,53,54.
Particle-phase chemical composition was quantified using a high-resolution time-of-flight aerosol mass spectrometer (HR-ToF-AMS, Aerodyne Research). The working principles of the HR-ToF-AMS have been explained in detail previously55,56. In brief, particles are focused by an aerodynamic lens and flash-vaporized by impact onto a hot surface at 600 °C under a high vacuum. The vapours are then ionized by 70-eV electrons and the ions are detected with a ToF mass spectrometer. Ionization efficiency calibrations were conducted before and after the campaign and the variation is within 30%. The particle collection efficiency was considered constant during the experiments because temperature and relative humidity in the chamber were fixed and the particle composition was dominated by ammonium nitrate.
INP were measured in real time at 215 K, as a function of ice saturation ratio (Sice), by the mobile ice nucleation instrument of the Karlsruhe Institute of Technology (mINKA). mINKA is a continuous flow diffusion chamber with vertical cylindrical geometry57, on the basis of the design of INKA58,59. A detailed description of the continuous flow diffusion chamber working principle is presented elsewhere57. Here, predefined scans of the water vapour saturation ratios were performed in the diffusion chamber every 30 min. For each scan, Sice steadily increased from 1.2 to 1.8 while the temperature was kept constant. The errors associated to temperature and Sice inside the diffusion chamber were derived from the uncertainty of the thermocouples attached to the instrument walls (±0.5 K)59.
Determination of particle formation rate
The particle formation rate, J1.7, is determined at 1.7-nm mobility diameter (1.4-nm physical diameter), here using a PSM. At 1.7 nm, a particle is normally considered to be above its critical size and, therefore, thermodynamically stable. J1.7 is calculated using the flux of the total concentration of particles growing past a specific diameter (here at 1.7 nm), as well as correction terms accounting for aerosol losses owing to dilution in the chamber, wall losses and coagulation. Details were described previously47.
Nucleation model
The nucleation model is on the basis of the thermodynamic model for H2SO4–NH3 nucleation described in detail previously18,19. It is developed from the general dynamic equations60, to calculate the production and losses for each cluster/particle size to determine the formation rates of the acid–base clusters. For HNO3–H2SO4–NH3 nucleation, we simplify the model simulations by extrapolating nano-Köhler-type activation by nitric acid and ammonia to clusters down to sulfuric acid trimers. Eighty size bins, ranging from one ammonium sulfate cluster to 300 nm, are used to capture the evolution of the size and composition of polydisperse particles.
In brief, we calculate the equimolar condensation flux of nitric acid and ammonia on the basis of the supersaturation of gas-phase nitric acid and ammonia over particle-phase ammonium nitrate39,60:
in which \({\Phi }_{i}^{v}\) is the net condensation flux of nitric acid or ammonia, with vapour concentration \({C}_{i}^{v}\) and saturation concentration \({C}_{i}^{0}\). The term ai is the activity of species i at the condensed-phase surface of the particle and kc is the condensation sink for vapours resulting from interaction with particles. The saturation concentrations of nitric acid and ammonia are estimated on the basis of the dissociation constant Kp (ref. 60). When the vapours are unsaturated, particle-phase ammonium nitrate will evaporate to nitric acid and ammonia to reach the equilibrium.
We also include the Kelvin term (Ki,p) in the simulation to account for the increased activity \(({a}_{i}={a{\prime} }_{i}\,{K}_{i,p})\) of a small curved cluster/particle:
in which Ki,p scales with a ‘Kelvin diameter’ (dK10) for decadal change and dp is the diameter of the small cluster/particle. The Kelvin diameter for ammonium nitrate is estimated to be 5.3 nm by fitting the data from previous CLOUD experiments according to:
in which S is the saturation ratio, calculated by means of dividing the product of measured concentrations of nitric acid and ammonia by the dissociation constant Kp and dact is the activation diameter, at which the thermodynamic energy barrier for condensation is overcome and particles start to grow rapidly.
Determination of ice nucleation ability
During the experiments, aerosol particles were continuously sampled from the CLOUD chamber into the mINKA ice nucleation instrument, using an actively cooled sampling line for a consistent temperature profile. Particles were then subject to well-controlled ice supersaturated conditions; the ones that nucleated ice were selectively detected and counted by an optical particle counter (custom-modified Climet CI-3100, lower detection limit of about 1 μm) located at the outlet of the instrument. Background ice crystals were quantified before each saturation scan (for 2 min) and subtracted from the total ice number concentration of the corresponding measurement. The fraction of INP (fice) was calculated as the ratio of ice crystals number concentration to the total number of particles larger than 10 nm in diameter. The ice nucleation active surface site density (ns)61 was calculated as the ratio of ice number concentration to the total surface area of particles larger than 10 nm in diameter. The overall uncertainty of ns is estimated to be ±40% (ref. 24). Particle number and surface area concentrations were measured by the SMPS described in the ‘Instrumentation’ section.
In Extended Data Fig. 4, we provide a detailed summary of the measurement data recorded during the ‘hotspot condition’ experiment shown in Fig. 4a, in which we investigated the heterogeneous crystallization and ice nucleation ability of ammonium nitrate/sulfate particles produced directly from new particle formation. We first formed pure ammonium nitrate particles through nucleation of nitric acid and ammonia vapours at 223 K and 15–30% relative humidity (over liquid water). When the evolution of the particle size distribution (Extended Data Fig. 4a) levelled off at a median diameter of around 100 nm, we turned on the UV lights and progressively injected SO2 at 03:33 to gradually increase sulfuric acid concentration (Extended Data Fig. 4b). Consequently, in Extended Data Fig. 4c, aerosol mass spectrometer measurements show that particle composition was dominated by ammonium nitrate over the course of the experiment, whereas sulfate appeared approximately 1 h after the injection of SO2. Finally, we show ice nucleation measurements in Extended Data Fig. 4d. Each vertical trajectory represents a saturation ratio scan in mINKA, colour-coded by the measured ice active fraction (fice). In each scan, we use a horizontal black dash to indicate an ice onset threshold corresponding to fice of 10−3. Circles indicate the corresponding scans shown in Fig. 4a.
When the particulate sulfate-to-nitrate molar ratio is smaller than 0.0001, the ice nucleation threshold is detected at an ice saturation ratio (Sice) of about 1.6, consistent with the homogeneous freezing threshold of aqueous solution droplets62. This finding shows that, if particles presented as absolutely pure ammonium nitrate (NH4NO3), they would exist as supercooled liquid droplets even at very low relative humidity, consistent with previous studies22,63. As the particulate sulfate-to-nitrate molar ratio gradually increases to about 0.017, the ice nucleation onset shifts to a lower Sice of 1.2, caused by heterogeneous ice nucleation on crystalline ammonium nitrate particles23. Crystalline salts are known to be efficient INP at low temperatures when their deliquescence occurs at higher relative humidity compared with the humidity range of their heterogeneous ice nucleation activity64. The fact that the addition of sulfate can promote the crystallization of ammonium nitrate has already been observed in previous studies with particles nebulized in large sizes (around 1 μm) from bulk solutions of ammonium nitrate/sulfate6,23,65. But it is evidenced here for the first time in an in situ particle nucleation and crystallization experiment representative of upper tropospheric conditions.
Particle formation rate parameterization
According to the first nucleation theorem for multicomponent systems25, we parameterize the particle formation rates (J1.7) for the HNO3–H2SO4–NH3 nucleation scheme with the empirical formula:
in which vapour concentrations are in units of cm−3 and k, a, b and c are free parameters. This method has been validated by previous observations that the particle formation rates (J1.7) vary as a product of power-law functions of nucleating vapours. For example, J1.7 for ternary sulfuric acid, ammonia (and water) nucleation follows a cubic dependency on sulfuric acid8 and a linear8 or quadratic19 dependency on ammonia; J1.7 for multicomponent nucleation of sulfuric acid, biogenic oxidized organics and ammonia follows a quadratic dependency on sulfuric acid, a linear dependency on both organics66 and ammonia11. The prefactor k accounts for effects of external conditions, such as temperature and relative humidity, thus differs in different environments.
To isolate variables, here we fit the power-law exponents for sulfuric acid, nitric acid and ammonia, respectively, to the dataset of experiments in which only the corresponding vapour concentration was varied. The red triangles, blue circles and yellow squares in Extended Data Fig. 5a–c (same experiments in Extended Data Fig. 1, Fig. 1 and Extended Data Fig. 2), respectively, show that J1.7 depends on [H2SO4]3 for sulfuric acid between 2.6 × 105 and 2.9 × 106 cm−3 (or 0.008 and 0.09 pptv), on [HNO3]2 for nitric acid between 2.3 × 108 and 1.7 × 109 cm−3 (or 7 and 52 pptv) and on [NH3]4 for ammonia between 1.7 × 108 and 4.9 × 108 cm−3 (or 5 and 15 pptv). The third power exponent for sulfuric acid is consistent with previously reported parameterizations for ternary H2SO4–NH3 nucleation8,19. The fourth power exponent for ammonia, however, is larger than those in ternary8,19 or multicomponent systems11, which emphasizes the critical role of ammonia and suggests further bonding between ammonia and nitric acid molecules in the nucleating clusters. Next, we verify the exponents by refitting the product of [H2SO4]3, [HNO3]2 and [NH3]4 to the full dataset. Extended Data Fig. 5d shows good consistency (R2 = 0.9) of the parameterization among the three experiments, with a slope of 3.4 × 10−71 s−1 cm24 being the prefactor k:
This parameterization is representative of new particle formation in the Asian monsoon upper troposphere because our experimental conditions of 223 K and 25% relative humidity, as well as concentrations of sulfuric acid67,68 and nitric acid69,70, are within the upper tropospheric range, with ammonia5,6 typical of Asian monsoon regions. One caveat, however, is that the cosmic radiation was at the ground level in our chamber, as shown with grey dot-dashed horizontal line in Extended Data Fig. 5d. The ion-pair production rate can be up to ten times higher in the ambient upper troposphere71, potentially leading to further enhancement of J1.7 by ion-induced nucleation, although the neutral channel dominates in our experiments.
Estimated temperature dependence of the particle formation rate
We did not cover the full temperature range in the upper troposphere, instead focusing on 223 K. However, to make the parameterization in the previous section more applicable for model simulations while not overstating the role of this mechanism, we provide some constraints on the temperature dependence of J1.7 for HNO3–H2SO4–NH3 nucleation. Broadly, it is certain that particle formation involving HNO3 will have a strong temperature dependence, becoming much slower as T increases.
We first present the temperature dependence of J1.7 for pure HNO3–NH3 nucleation with the expression:
in which k(T) is an empirical temperature-dependent rate constant and has the Arrhenius form
in which T is the absolute temperature (in Kelvin), E is the activation energy and R is the universal gas constant. f([HNO3],[NH3]) is a function of the ammonia and nitric acid concentrations (including the pre-exponential factor and free-fitting parameters). This expression is then fitted to the dataset in Fig. 3c in our previous study16, in which J1.7 were measured with only nitric acid, ammonia and water vapours added to the chamber, and the temperature was progressively decreased from 258 K to 249 K. Because the ammonia and nitric acid concentrations were kept almost constant during the temperature transition, we treat the f([HNO3],[NH3]) term as a constant to reduce the degrees of freedom. This expression with its two free parameters leads to a good agreement with the data, R2 = 0.96. And the fitted −E/R and f([HNO3],[NH3]) are 14,000 K and 3.2 × 10−26, respectively.
Next, we apply the same k(T) term to the HNO3–H2SO4–NH3 parameterization (equation (9)), assuming that the multicomponent nucleation follows a similar temperature dependence:
Although this temperature-dependent parameterization may not be the final description of this process, it tracks the trend of J1.7 well. In the event of 4 × 106 cm−3 H2SO4, 1.5 × 109 cm−3 HNO3 and 5 × 108 cm−3 NH3, the multicomponent nucleation is quenched (J1.7 < 0.01 cm−3 s−1) above 268 K. This is consistent with the observations that nitric acid and ammonia only contribute to the growth of ammonium sulfate particles at 278 K (ref. 16). At 223 K, the parameterized J1.7 is 306 cm−3 s−1, matching our measurement in Fig. 2. And for the temperature in the upper troposphere and lower stratosphere (198 K), the parameterized J1.7 is 8 × 105 cm−3 s−1, which is still much slower than its kinetic limit of about 109–1010 cm−3 s−1.
The EMAC global model
The ECHAM/MESSy Atmospheric Chemistry (EMAC) model is a numerical chemistry and climate simulation system that includes sub-models describing tropospheric and middle atmosphere processes and their interaction with oceans, land and human influences72. It uses the second version of the Modular Earth Submodel System (MESSy2) to link multi-institutional computer codes. Atmospheric circulation is calculated by the 5th generation of the European Centre Hamburg general circulation model (ECHAM5 (ref. 73)) and atmospheric chemical kinetics are solved for every model time step. For the present study, we applied EMAC (ECHAM5 version 5.3.02, MESSy version 2.54.0) in the T42L31ECMWF-resolution, for example, with a spherical truncation of T42 (corresponding to a quadratic Gaussian grid of approximately 2.8° by 2.8° in latitude and longitude) with 31 vertical hybrid pressure levels up to 10 hPa. EMAC uses a modal representation of aerosols dynamics (GMXe) that describes the aerosol size distribution as seven interacting log-normal distributions, of which four modes are soluble and three modes are insoluble. New particles are added directly to the nucleation mode. The applied model setup comprises the sub-model New Aerosol Nucleation (NAN) that includes new parameterizations of aerosol particle formation rates published in recent years74. These parameterizations include ion-induced nucleation. The ion-pair production rate, needed to calculate the ion-induced or ion-mediated nucleation, is described using the sub-model IONS, which provides ion-pair production rates74.
The TOMCAT global model
The TOMCAT model is a global 3D offline chemical transport model75,76. It is run at approximately 2.8° spatial resolution, such as EMAC on a T42 grid, driven by ECMWF ERA-Interim reanalysis meteorological fields for the year 2008. We also used 31 hybrid sigma-pressure levels from the surface to 10 hPa. The dissolved fraction of gases in cloud water is calculated by means of an equilibrium Henry’s law approach and set to zero for temperatures below −20 °C. The model includes GLOMAP aerosol microphysics77 with nitrate and ammonium from the HyDIS solver78 and the representation of new particle formation used by Gordon et al.3. The HyDIS solver adopts a sophisticated approach to the dissolution of nitric acid and ammonia into the aerosol phase that is a hybrid between a dynamic representation of the process, which accounts for the time needed for mass transport, and an equilibrium representation, which does not78. The main limitation of the solver is that it assumes all aerosol particles are liquid, which is probably a poor approximation in cold, dry conditions frequently found in the upper troposphere.
The cloud trajectories framework
We conducted a sensitivity study on ammonia transport processes and estimated the fraction remaining of ammonia vapour after convection from the boundary layer to the upper troposphere, using a cloud trajectories framework described in detail in Bardakov et al.79,80. In brief, trajectories from a convective system simulated with the large-eddy simulation (LES) model MIMICA81 were extracted and a parcel representing the cloud outflow was selected for further analysis (Extended Data Fig. 8a). The meteorological profiles and clouds microphysics scheme used here were the same as in Bardakov et al.80, producing altitude-dependent distributions of water and ice hydrometeors depicted in Extended Data Fig. 8. Partitioning of gas between vapour and aqueous phase along the trajectory was calculated on the basis of Henry’s law constant adjusted to a cloud pH, H* = H × 1.7 × 10(9−pH) following the expression for ammonia from Seinfeld and Pandis60.
We then investigated the factors governing ammonia transport through the simulated convective system by varying: (1) the pH for the liquid water hydrometeors (Extended Data Fig. 8c); (2) the total amount of water in the system (Extended Data Fig. 8d); (3) the retention of ammonia molecules by the ice hydrometeors (Extended Data Fig. 8e). In our base-case simulation, the pH was assumed to have an altitude-dependent profile, reflecting the higher abundance of acids close to the surface and ranging from 4.5 to 5, in accordance with the representative pH values in the EMAC simulation. The base-case water content was as in Bardakov et al.80 and the ice retention coefficient 0.05 in accordance with Ge et al.13, with no further uptake on ice.
Atmospheric interpretation
This work focuses on the Asian monsoon region in part because this region is fairly extensive, but also because ammonia concentrations measured in this region are by far the highest in the upper troposphere. Although we frame this synergistic HNO3–H2SO4–NH3 nucleation in a scenario that suits the Asian monsoon upper troposphere, the physics applies more broadly — the colder the conditions are, the more important this mechanism is likely to be. To explore the importance of this synergistic nucleation to the atmosphere, we combine our experimental results, cloud resolving modelling and global-scale chemical transport modelling. On the basis of these constraints, the rate-limiting elements of new particle formation seem to be convective transport of ammonia and the production rate of particles in the mixing zone between convective outflow and the background upper free troposphere; however, confirmation of this will require extensive field and modelling studies.
Generally, nitric acid ranges between about 108 and 109 cm−3 (refs. 14,15) and sulfuric acid between about 105 and 106 cm−3 (refs. 82,83) in the tropical upper troposphere. The typical acid-excess conditions leave the principal uncertainty being ammonia levels, which are not yet well constrained. Although satellite-based ammonia measurements have provided a spatial distribution on a global scale, they are limited to cloud-free areas owing to blockage of the ammonia signal by optically thick clouds. However, deep convection followed by cloud glaciation may be a major source of upper tropospheric ammonia. This process may then not be captured by satellites as it occurs near clouds, with short time duration and high spatial heterogeneity. This may also explain why the in situ-measured ammonia concentrations are up to 40 times higher than those from satellite measurements6.
Ammonia has no known chemical source in the atmosphere but is instead transported by cloud processes from the surface, whereas nitric acid and sulfuric acid vapours are formed primarily by out-of-cloud oxidation. Consequently, it is probable that this synergistic nucleation occurs initially in the outflow of convective clouds, in which the released ammonia mixes with pre-existing (background) nitric acid and sulfuric acid. Subsequently, as ammonia is titrated over several e-folding times (governed by the condensation sink in this mixing zone) and the outflow air fully mixes with the background air, nucleation conditions will shift from the ammonia-rich regime to the ammonia-limited regime. These highly dynamic processes are thus the key to constraining the climatic effects of this synergistic nucleation in Asian monsoon and potentially other convective regions. Nevertheless, current ambient measurements confirm the presence of ample ammonia, as well as particles comprised largely of ammonium nitrate4, and our experiments show that synergistic HNO3–H2SO4–NH3 nucleation is a viable mechanism for new particle formation in the Asian monsoon upper troposphere. As global ammonia emissions continue to increase owing to agricultural growth and the warmer climate84,85, the importance of this particle formation mechanism will increase.
Further, as there is almost no in situ composition measurement of clusters or newly formed particles in the upper troposphere, we can only infer the major particle formation pathway from indirect evidence such as composition of precursor vapours or larger particles. Previously established mechanisms include binary and ternary sulfuric acid nucleation, which drive new particle formation over marine or anthropogenically influenced regions1,4,86,87, nucleation by oxygenated organics, which dominates over pristine vegetated areas such as the Amazon basin2,10,88, and nucleation by iodine oxidation products, which may be especially important in marine convection89,90. Over the Asian monsoon regions, however, mixed emissions of both inorganic and organic vapours may well complicate the particle formation mechanism. However, it has been demonstrated that ammonium nitrate can often explain more than half of the particulate volume in the upper troposphere6. This means that the HNO3–NH3 concentration is probably higher than the sum of all other condensable vapours (that is, sulfuric acid and oxygenated organics). And given that HNO3–H2SO4–NH3 nucleation is orders of magnitude faster than binary and ternary sulfuric acid nucleation at observed ammonia levels, we therefore infer that synergistic HNO3–H2SO4–NH3 nucleation is a major particle formation pathway in the Asian monsoon upper troposphere. It seems unlikely that this inorganic pathway and the organic pathways are antagonistic in growth, and without strong indications otherwise, it seems probable that they are more or less additive for nucleation itself. However, to further investigate interactions between different nucleation schemes, we would rely on further information on the source and identity of organic vapours that are present in the Asian monsoon upper troposphere.
Data availability
The full dataset shown in the figures is publicly available at https://doi.org/10.5281/zenodo.5949440. Source data are provided with this paper.
Code availability
The EMAC (ECHAM/MESSy) model is continuously further developed and applied by a consortium of institutions. The use of MESSy and access to the source code is licensed to all affiliates of institutions that are members of the MESSy Consortium. Institutions can become a member of the MESSy Consortium by signing the MESSy Memorandum of Understanding. More information can be found on the MESSy Consortium website (https://www.messy-interface.org). All code modifications presented in this paper will be included in the next version of MESSy. The TOMCAT model (http://homepages.see.leeds.ac.uk/~lecmc/tomcat.html) is a UK community model. It is available to UK (or NERC-funded) researchers who normally access the model on common facilities or who are helped to install it on their local machines. As it is a complex research tool, new users will need help to use the model optimally. We do not have the resources to release and support the model in an open way. Any potential user interested in the model should contact Martyn Chipperfield. The model updates described in this paper are included in the standard model library. The cloud trajectories model is publicly available at https://doi.org/10.5281/zenodo.5949440. Codes for conducting the analysis presented in this paper can be obtained by contacting the corresponding author, Neil M. Donahue (nmd@andrew.cmu.edu).
References
Clarke, A. et al. Nucleation in the equatorial free troposphere: favorable environments during PEM-Tropics. J. Geophys. Res. Atmos. 104, 5735–5744 (1999).
Weigel, R. et al. In situ observations of new particle formation in the tropical upper troposphere: the role of clouds and the nucleation mechanism. Atmos. Chem. Phys. 11, 9983–10010 (2011).
Gordon, H. et al. Causes and importance of new particle formation in the present-day and pre-industrial atmospheres. J. Geophys. Res. Atmos. 122, 8739–8760 (2017).
Williamson, C. J. et al. A large source of cloud condensation nuclei from new particle formation in the tropics. Nature 574, 399–403 (2019).
Höpfner, M. et al. First detection of ammonia (NH3) in the Asian summer monsoon upper troposphere. Atmos. Chem. Phys. 16, 14357–14369 (2016).
Höpfner, M. et al. Ammonium nitrate particles formed in upper troposphere from ground ammonia sources during Asian monsoons. Nat. Geosci. 12, 608–612 (2019).
Intergovernmental Panel on Climate Change. Climate Change 2013: The Physical Science Basis (Cambridge Univ. Press, 2013).
Dunne, E. M. et al. Global atmospheric particle formation from CERN CLOUD measurements. Science 354, 1119–1124 (2016).
Kirkby, J. et al. Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation. Nature 476, 429–433 (2011).
Andreae, M. O. et al. Aerosol characteristics and particle production in the upper troposphere over the Amazon Basin. Atmos. Chem. Phys. 18, 921–961 (2018).
Lehtipalo, K. et al. Multicomponent new particle formation from sulfuric acid, ammonia, and biogenic vapors. Sci. Adv. 4, eaau5363 (2018).
Zhao, B. et al. High concentration of ultrafine particles in the Amazon free troposphere produced by organic new particle formation. Proc. Natl Acad. Sci. 117, 25344–25351 (2020).
Ge, C., Zhu, C., Francisco, J. S., Zeng, X. C. & Wang, J. A molecular perspective for global modeling of upper atmospheric NH3 from freezing clouds. Proc. Natl Acad. Sci. 115, 6147–6152 (2018).
Martin, R. V. et al. Space-based constraints on the production of nitric oxide by lightning. J. Geophys. Res. Atmos. 112, D09309 (2007).
Lelieveld, J. et al. The South Asian monsoon—pollution pump and purifier. Science 361, 270–273 (2018).
Wang, M. et al. Rapid growth of atmospheric nanoparticles by nitric acid and ammonia condensation. Nature 580, 184–189 (2020).
Stolzenburg, D. et al. Enhanced growth rate of atmospheric particles from sulfuric acid. Atmos. Chem. Phys. 20, 7359–7372 (2020).
Kürten, A. New particle formation from sulfuric acid and ammonia: nucleation and growth model based on thermodynamics derived from CLOUD measurements for a wide range of conditions. Atmos. Chem. Phys. 19, 5033–5050 (2019).
Xiao, M. et al. The driving factors of new particle formation and growth in the polluted boundary layer. Atmos. Chem. Phys. 21, 14275–14291 (2021).
Ehrhart, S. & Curtius, J. Influence of aerosol lifetime on the interpretation of nucleation experiments with respect to the first nucleation theorem. Atmos. Chem. Phys. 13, 11465–11471 (2013).
Schobesberger, S. et al. Molecular understanding of atmospheric particle formation from sulfuric acid and large oxidized organic molecules. Proc. Natl Acad. Sci. 110, 17223–17228 (2013).
Martin, S. T. Phase transitions of aqueous atmospheric particles. Chem. Rev. 100, 3403–3454 (2000).
Wagner, R. et al. Solid ammonium nitrate aerosols as efficient ice nucleating particles at cirrus temperatures. J. Geophys. Res. Atmos. 125, e2019JD032248 (2020).
Ullrich, R. et al. A new ice nucleation active site parameterization for desert dust and soot. J. Atmos. Sci. 74, 699–717 (2017).
Oxtoby, D. W. & Kashchiev, D. A general relation between the nucleation work and the size of the nucleus in multicomponent nucleation. J. Chem. Phys. 100, 7665–7671 (1994).
Kille, N. et al. The CU mobile solar occultation flux instrument: structure functions and emission rates of NH3, NO2 and C2H6. Atmos. Meas. Tech. 10, 373–392 (2017).
Nault, B. A. et al. Chemical transport models often underestimate inorganic aerosol acidity in remote regions of the atmosphere. Commun. Earth Environ. 2, 93 (2021).
Warner, J. X., Wei, Z., Strow, L. L., Dickerson, R. R. & Nowak, J. B. The global tropospheric ammonia distribution as seen in the 13-year AIRS measurement record. Atmos. Chem. Phys. 16, 5467–5479 (2016).
Williams, J., Reus, M. D., Krejci, R., Fischer, H. & Ström, J. Application of the variability-size relationship to atmospheric aerosol studies: estimating aerosol lifetimes and ages. Atmos. Chem. Phys. 2, 133–145 (2002).
Duplissy, J. et al. Effect of ions on sulfuric acid-water binary particle formation: 2. Experimental data and comparison with QC-normalized classical nucleation theory. J. Geophys. Res. Atmos. 212, 1752–1775 (2016).
Dias, A. et al. Temperature uniformity in the CERN CLOUD chamber. Atmos. Meas. Tech. 10, 5075–5088 (2017).
Kirkby, J. et al. Ion-induced nucleation of pure biogenic particles. Nature 530, 521–526 (2016).
Schnitzhofer, R. et al. Characterisation of organic contaminants in the CLOUD chamber at CERN. Atmos. Meas. Tech. 7, 2159–2168 (2014).
Jokinen, T. et al. Atmospheric sulphuric acid and neutral cluster measurements using CI-APi-TOF. Atmos. Chem. Phys. 12, 4117–4125 (2012).
Kürten, A. et al. Neutral molecular cluster formation of sulfuric acid–dimethylamine observed in real time under atmospheric conditions. Proc. Natl Acad. Sci. 111, 15019–15024 (2014).
Lopez-Hilfiker, F. D. et al. A novel method for online analysis of gas and particle composition: description and evaluation of a Filter Inlet for Gases and AEROsols (FIGAERO). Atmos. Meas. Tech. 7, 983–1001 (2014).
Wang, M. et al. Reactions of atmospheric particulate stabilized Criegee intermediates lead to high-molecular-weight aerosol components. Environ. Sci. Technol. 50, 5702–5710 (2016).
Kürten, A., Rondo, L., Ehrhart, S. & Curtius, J. Performance of a corona ion source for measurement of sulfuric acid by chemical ionization mass spectrometry. Atmos. Meas. Tech. 4, 437–443 (2011).
Tröstl, J. et al. The role of low-volatility organic compounds in initial particle growth in the atmosphere. Nature 530, 527–531 (2016).
Breitenlechner, M. et al. PTR3: an instrument for studying the lifecycle of reactive organic carbon in the atmosphere. Anal. Chem. 89, 5824–5831 (2017).
Kürten, A. et al. Experimental particle formation rates spanning tropospheric sulfuric acid and ammonia abundances, ion production rates, and temperatures. J. Geophys. Res. Atmos. 121, 12–377 (2016).
McMurry, P. H. & Grosjean, D. Gas and aerosol wall losses in Teflon film smog chambers. Environ. Sci. Technol. 19, 1176–1181 (1985).
Simon, M. et al. Molecular insight into HOM formation and biogenic new-particle formation over a wide range of tropospheric temperatures. Atmos. Chem. Phys. 20, 9183–9207 (2020).
Tang, M., Cox, R. & Kalberer, M. Compilation and evaluation of gas phase diffusion coefficients of reactive trace gases in the atmosphere: volume 1. inorganic compounds. Atmos. Chem. Phys. 14, 9233–9247 (2014).
Junninen, H. et al. A high-resolution mass spectrometer to measure atmospheric ion composition. Atmos. Meas. Tech. 3, 1039–1053 (2010).
Kürten, A. et al. Observation of new particle formation and measurement of sulfuric acid, ammonia, amines and highly oxidized organic molecules at a rural site in central Germany. Atmos. Chem. Phys. 16, 12793–12813 (2016).
Dada, L. et al. Formation and growth of sub-3-nm aerosol particles in experimental chambers. Nat. Protoc. 15, 1013–1040 (2020).
Mui, W., Mai, H., Downard, A. J., Seinfeld, J. H. & Flagan, R. C. Design, simulation, and characterization of a radial opposed migration ion and aerosol classifier (ROMIAC). Aerosol Sci. Technol. 51, 801–823 (2017).
Wimmer, D. et al. Performance of diethylene glycol-based particle counters in the sub-3 nm size range. Atmos. Meas. Tech. 6, 1793–1804 (2013).
Mai, H. & Flagan, R. C. Scanning DMA data analysis I. Classification transfer function. Aerosol Sci. Technol. 52, 1382–1399 (2018).
Mai, H., Kong, W., Seinfeld, J. H. & Flagan, R. C. Scanning DMA data analysis II. Integrated DMA-CPC instrument response and data inversion. Aerosol Sci. Technol. 52, 1400–1414 (2018).
Jurányi, Z. et al. A 17 month climatology of the cloud condensation nuclei number concentration at the high alpine site Jungfraujoch. J. Geophys. Res. Atmos. 116, D10204 (2011).
Tröstl, J. et al. Fast and precise measurement in the sub-20 nm size range using a Scanning Mobility Particle Sizer. J. Aerosol Sci. 87, 75–87 (2015).
Wiedensohler, A. et al. Mobility particle size spectrometers: harmonization of technical standards and data structure to facilitate high quality long-term observations of atmospheric particle number size distributions. Atmos. Meas. Tech. 5, 657–685 (2012).
Jayne, J. T. et al. Development of an aerosol mass spectrometer for size and composition analysis of submicron particles. Aerosol Sci. Technol. 33, 49–70 (2000).
DeCarlo, P. F. et al. Field-deployable, high-resolution, time-of-flight aerosol mass spectrometer. Anal. Chem. 78, 8281–8289 (2006).
Rogers, D. C. Development of a continuous flow thermal gradient diffusion chamber for ice nucleation studies. Atmos. Res. 22, 149–181 (1988).
DeMott, P. J. et al. The Fifth International Workshop on Ice Nucleation phase 2 (FIN-02): laboratory intercomparison of ice nucleation measurements. Atmos. Meas. Tech. 11, 6231–6257 (2018).
Schiebel, T. Ice Nucleation Activity of Soil Dust Aerosols. PhD thesis, KIT-Bibliothek (2017).
Seinfeld, J. H. & Pandis, S. N. Atmospheric Chemistry and Physics 2nd edn (Wiley, 2006).
Connolly, P. J. et al. Studies of heterogeneous freezing by three different desert dust samples. Atmos. Chem. Phys. 9, 2805–2824 (2009).
Koop, T., Luo, B., Tsias, A. & Peter, T. Water activity as the determinant for homogeneous ice nucleation in aqueous solutions. Nature 406, 611–614 (2000).
Cziczo, D. J. & Abbatt, J. P. D. Infrared observations of the response of NaCl, MgCl2, NH4HSO4, and NH4NO3 aerosols to changes in relative humidity from 298 to 238 K. J. Phys. Chem. A 104, 2038–2047 (2000).
Zuberi, B., Bertram, A. K., Koop, T., Molina, L. T. & Molina, M. J. Heterogeneous freezing of aqueous particles induced by crystallized (NH4)2SO4, ice, and letovicite. J. Phys. Chem. A 105, 6458–6464 (2001).
Schlenker, J. C. & Martin, S. T. Crystallization pathways of sulfate–nitrate–ammonium aerosol particles. J. Phys. Chem. A 109, 9980–9985 (2005).
Riccobono, F. et al. Oxidation products of biogenic emissions contribute to nucleation of atmospheric particles. Science 344, 717–721 (2014).
Möhler, O. & Arnold, F. Gaseous sulfuric acid and sulfur dioxide measurements in the Arctic troposphere and lower stratosphere: implications for hydroxyl radical abundances. Geophys. Res. Lett. 19, 1763–1766 (1992).
Williamson, C. J. et al. Large hemispheric difference in ultrafine aerosol concentrations in the lowermost stratosphere at mid and high latitudes. Atmos. Chem. Phys. Discuss. 1–44 (2021).
Wespes, C. et al. First global distributions of nitric acid in the troposphere and the stratosphere derived from infrared satellite measurements. J. Geophys. Res. Atmos. 112, D13311 (2007).
Popp, P. et al. Stratospheric correlation between nitric acid and ozone. J. Geophys. Res. Atmos. 114, D03305 (2009).
Hirsikko, A. et al. Atmospheric ions and nucleation: a review of observations. Atmos. Chem. Phys. 11, 767–798 (2011).
Jöckel, P. et al. Development cycle 2 of the modular earth submodel system (MESSy2). Geosci. Model Dev. 3, 717–752 (2010).
Roeckner, E. et al. Sensitivity of simulated climate to horizontal and vertical resolution in the ECHAM5 atmosphere model. J. Clim. 19, 3771–3791 (2006).
Ehrhart, S. et al. Two new submodels for the Modular Earth Submodel System (MESSy): New Aerosol Nucleation (NAN) and small ions (IONS) version 1.0. Geosci. Model Dev. 11, 4987–5001 (2018).
Chipperfield, M. New version of the TOMCAT/SLIMCAT off-line chemical transport model: Intercomparison of stratospheric tracer experiments. Q. J. R. Meteorol. Soc. 132, 1179–1203 (2006).
Monks, S. A. et al. The TOMCAT global chemical transport model v1.6: description of chemical mechanism and model evaluation. Geosci. Model Dev. 10, 3025–3057 (2017).
Mann, G. et al. Description and evaluation of GLOMAP-mode: a modal global aerosol microphysics model for the UKCA composition-climate model. Geosci. Model Dev. 3, 519–551 (2010).
Benduhn, F. et al. Size-resolved simulations of the aerosol inorganic composition with the new hybrid dissolution solver HyDiS-1.0: description, evaluation and first global modelling results. Geosci. Model Dev. 9, 3875–3906 (2016).
Bardakov, R. et al. A novel framework to study trace gas transport in deep convective clouds. J. Adv. Model. Earth Syst. 12, e2019MS001931 (2020).
Bardakov, R., Thornton, J. A., Riipinen, I., Krejci, R. & Ekman, A. M. L. Transport and chemistry of isoprene and its oxidation products in deep convective clouds. Tellus B Chem. Phys. Meteorol. 73, 1–21 (2021).
Savre, J., Ekman, A. M. L. & Svensson, G. Technical note: Introduction to MIMICA, a large-eddy simulation solver for cloudy planetary boundary layers. J. Adv. Model. Earth Syst. 6, 630–649 (2014).
Bates, T. S., Huebert, B. J., Gras, J. L., Griffiths, F. B. & Durkee, P. A. International Global Atmospheric Chemistry (IGAC) project’s first aerosol characterization experiment (ACE 1): overview. J. Geophys. Res. Atmos. 103, 16297–16318 (1998).
Hoell, J. M. et al. Pacific Exploratory Mission in the tropical Pacific: PEM-Tropics A, August-September 1996. J. Geophys. Res. Atmos. 104, 5567–5583 (1999).
Erisman, J. W., Sutton, M. A., Galloway, J., Klimont, Z. & Winiwarter, W. How a century of ammonia synthesis changed the world. Nat. Geosci. 1, 636–639 (2008).
Warner, J. X. et al. Increased atmospheric ammonia over the world’s major agricultural areas detected from space. Geophys. Res. Lett. 44, 2875–2884 (2017).
Twohy, C. H. et al. Deep convection as a source of new particles in the midlatitude upper troposphere. J. Geophys. Res. Atmos. 107, AAC 6-1–AAC 6-10 (2002).
Lee, S.-H. et al. Particle formation by ion nucleation in the upper troposphere and lower stratosphere. Science 301, 1886–1889 (2003).
Waddicor, D. A. et al. Aerosol observations and growth rates downwind of the anvil of a deep tropical thunderstorm. Atmos. Chem. Phys. 12, 6157–6172 (2012).
Wang, S. et al. Active and widespread halogen chemistry in the tropical and subtropical free troposphere. Proc. Natl Acad. Sci. 112, 9281–9286 (2015).
He, X.-C. et al. Role of iodine oxoacids in atmospheric aerosol nucleation. Science 371, 589–595 (2021).
Acknowledgements
We thank the European Organization for Nuclear Research (CERN) for supporting CLOUD with important technical and financial resources. This research has received funding from the US National Science Foundation (nos. AGS-1801574, AGS-1801897, AGS-1602086, AGS-1801329, AGS-2132089 and AGS-1801280), the European Union’s Horizon 2020 programme (Marie Skłodowska-Curie ITN no. 764991 ‘CLOUD-MOTION’), the European Commission, H2020 Research Infrastructures (FORCeS, no. 821205), the European Union’s Horizon 2020 research and innovation programme (Marie Skłodowska-Curie no. 895875 ‘NPF-PANDA’), a European Research Council (ERC) project ATM-GTP contract (no. 742206), an ERC-CoG grant INTEGRATE (no. 867599), the Swiss National Science Foundation (nos. 200021_169090, 200020_172602 and 20FI20_172622), the Academy of Finland ACCC Flagship (no. 337549), the Academy of Finland Academy professorship (no. 302958), the Academy of Finland (nos. 1325656, 316114 and 325647), Russian MegaGrant project ‘Megapolis – heat and pollution island: interdisciplinary hydroclimatic, geochemical and ecological analysis’ (application reference 2020-220-08-5835), Jane and Aatos Erkko Foundation ‘Quantifying carbon sink, CarbonSink+ and their interaction with air quality’ INAR project, Samsung PM2.5 SRP, Prince Albert Foundation ‘the Arena for the gap analysis of the existing Arctic Science Co-Operations (AASCO)’ (no. 2859), the German Federal Ministry of Education and Research (CLOUD-16 project nos. 01LK1601A and 01LK1601C), the Knut and Alice Wallenberg Foundation Wallenberg Academy Fellows project AtmoRemove (no. 2015.0162), the Portuguese Foundation for Science and Technology (no. CERN/FIS-COM/0014/2017) and the Technology Transfer Project N059 of the Karlsruhe Institute of Technology (KIT). The FIGAERO-CIMS was supported by a Major Research Instrumentation (MRI) grant for the US NSF AGS-1531284, as well as the Wallace Research Foundation. The computations by R.Bardakov were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Center (NSC). I.R. thanks the Max Planck Society for a sabbatical award. M.W. thanks Siebel Scholars Foundation for financial support.
Author information
Authors and Affiliations
Contributions
M.W., B.B., J.K. and N.M.D. planned the experiments. M.W., B.B., G.M., B.R., B.S., X.-C.H., J.S., W.S., R.M., B.L., H.L., H.E.M., F.A., P.B., Z.B., L.C., L.-P.D.M., J.D., H.F., L.G.C., M.G., R.G., V.H., A.K., K.L., V.M., D.M., S.M., R.L.M., B.M., T.M., A.O., T.P., M.P., A.A.P., A.P., M.Simon, Y.S., A.T., N.S.U., F.V., R.W., D.S.W., S.K.W., A.W., Y.W., M.Z.-W., M.Sipilä, P.M.W., A.H., U.B., M.K., R.C.F., J.C., R.V., I.E.-H., J.K., K.K. O.M., S.S. and N.M.D. prepared the CLOUD facility or measuring instruments. M.W., B.B., G.M., B.R., B.S., X.-C.H., J.S., W.S., R.M., B.L., H.E.M., A.A., L.C., L.G.C., M.G., M.H., V.H., J.E.K., N.G.A.M., D.M., R.L.M., B.M., A.R., M.Schervish, M.Simon, A.T., N.S.U., F.V., D.S.W., S.K.W., A.W., M.Z.-W., P.M.W., J.K. and K.K. collected the data. M.W., M.X., B.B., G.M., B.R., B.S., R.Bardakov, J.S., W.S., L.D., R.Baalbaki, B.L., D.S.W., S.K.W., A.W., I.R., T.C. and N.M.D. analysed the data. M.W., M.X., B.B., R.Bardakov, X.-C.H., J.S., W.S., R.M., L.D., R.Baalbaki., B.L., H.L., H.E.M., A.M.L.E., H.F., M.H., K.H., A.K., N.S.U., R.W., A.W., A.H., U.B., M.K., R.C.F., J.C., R.V., I.R., H.G., J.L., I.E.-H., D.R.W., T.C., J.K., O.M., S.S. and N.M.D. contributed to the scientific discussion. M.W., B.B., R.Bardakov, W.S., R.M., B.L., H.L., K.H., A.K., U.B., R.C.F., J.C., R.V., I.R., H.G., J.L., I.E.-H., T.C., J.K., O.M. and N.M.D. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature thanks Bernd Kärcher and the other, anonymous, reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Enhancement of HNO3–NH3 particle formation by sulfuric acid.
a, Particle number concentrations versus time at mobility diameters >1.7 nm (magenta) and >2.5 nm (green). The solid magenta trace is measured by a PSM1.7 and the solid green trace is measured by a CPC2.5. The fixed experimental conditions are about 6.5 × 108 cm−3 NH3, 223 K and 25% relative humidity. b, Particle formation rate versus time at 1.7 nm (J1.7), measured by a PSM. c, Particle size distribution versus time, measured by an SMPS. d, Gas-phase nitric acid and sulfuric acid versus time, measured by an I− CIMS and a NO3− CIMS, respectively. We started the experiment by oxidizing NO2 to produce 1.6 × 109 cm−3 HNO3 in the presence of about 6.5 × 108 cm−3 ammonia. At time = 0 min, we turned off the high-voltage clearing field to allow the ion concentration to build up to a steady state between GCR production and wall deposition. The presence of ions (GCR condition) induces slow HNO3–NH3 nucleation, followed by relatively fast particle growth by nitric acid and ammonia condensation. We thus observe formation of both 1.7-nm and 2.5-nm particles by about one order of magnitude in about 3.5 h, with a slower approach to steady state because of the longer wall deposition time constant for the larger particles. Then, we increased H2SO4 in the chamber from 0 to 4.9 × 106 cm−3 by oxidizing progressively more injected SO2 after 211 min, with a fixed production rate of nitric acid and injection rate of ammonia. Subsequently, particle concentrations increase by three orders of magnitude within 30 min. The overall systematic scale uncertainties of ±30% on particle formation rate, −33%/+50% on sulfuric acid concentration and ±25% on nitric acid concentration are not shown.
Extended Data Fig. 2 Enhancement of H2SO4–HNO3 nucleation by ammonia.
a, Particle number concentrations versus time at mobility diameters >1.7 nm (magenta) and >2.5 nm (green). The solid magenta trace is measured by a PSM1.7 and the solid green trace is measured by a CPC2.5. The fixed experimental conditions are 223 K and 25% relative humidity. b, Particle formation rate versus time at 1.7 nm (J1.7), measured by a PSM. c, Particle size distribution versus time, measured by an SMPS. d, Gas-phase nitric acid and sulfuric acid versus time, measured by an I− CIMS and a NO3− CIMS, respectively; gas-phase ammonia versus time, calculated with a first-order wall-loss rate. Before the experiment, we cleaned the chamber by rinsing the walls with ultra-pure water, followed by heating to 373 K and flushing at a high rate with humidified synthetic air for 48 h. We started with an almost perfectly clean chamber and only HNO3, SO2 and O3 vapours present at constant levels. Sulfuric acid starts to appear by means of SO2 oxidation soon after switching on the UV lights at time = 0 min, building up to a steady state of 5.0 × 106 cm−3 with the wall-loss timescale of about 10 min. Subsequently, we observe slow formation of 1.7-nm particles, yet they do not reach 2.5 nm during the course of a 2-h period with small growth rates and low survival probability. Then, owing to the injection of ammonia from 0 to around 6.5 × 108 cm−3 into the chamber after 80 min, a sharp increase in the rate of particle formation is observed with a fixed production rate of sulfuric acid and injection rate of nitric acid. The sulfuric acid concentration decreases slightly afterwards, owing to accumulated condensation sink from fast particle growth. The overall systematic scale uncertainties of ±30% on particle formation rate, −33%/50% on sulfuric acid concentration and ±25% on nitric acid concentration are not shown.
Extended Data Fig. 3 Particle formation rates at 1.7 nm (J1.7) versus ammonia concentration at 223 K and 25% relative humidity.
Circles are the CLOUD measurements (the same as those in Fig. 2). The curve represents the model simulations on the basis of known thermodynamics and microphysics, including Kelvin effects, for nucleating clusters.
Extended Data Fig. 4 Measurement of the ice nucleation ability of HNO3–H2SO4–NH3 particles versus sulfate-to-nitrate ratio.
a, Particle size distribution versus time during the experiment, measured by an SMPS. b, Gas-phase sulfuric acid versus time, measured by a nitrate CIMS. c, Particle-phase chemical composition versus time, measured by an AMS. d, Fraction of INP at the nominal temperature of 215 K. The horizontal black dashes indicate the ice fraction threshold, fice = 10−3. The coloured circles correspond to the sulfate-to-nitrate ratios shown in Fig. 4a.
Extended Data Fig. 5 Parameterization of the HNO3–H2SO4–NH3 particle formation rate.
a–c Particle formation rate (J1.7) as a function of H2SO4, HNO3 and NH3 vapour concentrations, respectively, at 223 K and 25% relative humidity. The red triangles, blue circles and yellow squares represent experiments while varying only the concentration of H2SO4 (Extended Data Fig. 1), HNO3 (Fig. 1) and NH3 (Extended Data Fig. 2), respectively. The H2SO4 concentration was varied between 4.6 × 105 and 2.9 × 106 cm−3, HNO3 between 2.3 × 108 and 1.7 × 109 cm−3 and NH3 between 1.8 × 108 and 5.1 × 108 cm−3. d, The multi-acid–ammonia parameterization (black line) on the basis of equation (6) with k = 3.4 × 10−71 s−1 cm24. The grey dashed horizontal line shows a maximum of about 2 cm−3 s−1 ion-induced nucleation in the CLOUD chamber under GCR conditions, limited by the ion-pair production rate from GCR plus beam-background muons. The bars indicate 30% estimated total error on the particle formation rates, although the overall systematic scale uncertainties of −33%/+50% on sulfuric acid concentration and ±25% on nitric acid concentration are not shown. e, Temperature dependence of J1.7 for HNO3–H2SO4–NH3 nucleation (blue curve) on the basis of equation (9) with k = 2.9 × 10−98 e14,000/T s−1 cm24.
Extended Data Fig. 6 Modelled contribution of HNO3–H2SO4–NH3 nucleation to upper tropospheric particles.
Number concentrations of multi-acid new particles (nucleation mode) at 250-hPa altitude simulated in a global model (EMAC) with efficient vertical transport of ammonia. The particle formation rate is on the basis of the blue dashed curve in Fig. 2 and parameterization shown in Extended Data Fig. 5. The extra particle number concentrations are shown, that is, relative to the same model without multi-acid nucleation. High annually averaged particle numbers are expected in the monsoon region (grey rectangle) and adjacent regions.
Extended Data Fig. 8 Modelled transport of ammonia to the upper troposphere in deep convective clouds.
a, Trajectories of the simulated convective cloud event (grey) and a selected parcel representing a buoyant parcel reaching the upper troposphere (black). b, The simulated evolution of parcel A altitude (green dashed trace) and the total mass concentration and phase of the cloud hydrometeors (red and blue curves). c–e Sensitivity of the predicted ammonia concentrations within parcel A to cloud water pH, total water amount and retention coefficient (by ice particles) as compared with the base-case simulation (blue trace in all figures).
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, M., Xiao, M., Bertozzi, B. et al. Synergistic HNO3–H2SO4–NH3 upper tropospheric particle formation. Nature 605, 483–489 (2022). https://doi.org/10.1038/s41586-022-04605-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04605-4
This article is cited by
-
Global variability in atmospheric new particle formation mechanisms
Nature (2024)
-
Recent advances in carbon-based catalysts for electrocatalytic nitrate reduction to ammonia
Carbon Letters (2024)
-
The impact of ammonia on particle formation in the Asian Tropopause Aerosol Layer
npj Climate and Atmospheric Science (2024)
-
Atmospheric new particle formation from the CERN CLOUD experiment
Nature Geoscience (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.