Abstract
Precisely engineered mechanical oscillators keep time, filter signals and sense motion, making them an indispensable part of the technological landscape of today. These unique capabilities motivate bringing mechanical devices into the quantum domain by interfacing them with engineered quantum circuits. Proposals to combine microwave-frequency mechanical resonators with superconducting devices suggest the possibility of powerful quantum acoustic processors1,2,3. Meanwhile, experiments in several mechanical systems have demonstrated quantum state control and readout4,5, phonon number resolution6,7 and phonon-mediated qubit–qubit interactions8,9. At present, these acoustic platforms lack processors capable of controlling the quantum states of several mechanical oscillators with a single qubit and the rapid quantum non-demolition measurements of mechanical states needed for error correction. Here we use a superconducting qubit to control and read out the quantum state of a pair of nanomechanical resonators. Our device is capable of fast qubit–mechanics swap operations, which we use to deterministically manipulate the mechanical states. By placing the qubit into the strong dispersive regime with both mechanical resonators simultaneously, we determine the phonon number distributions of the resonators by means of Ramsey measurements. Finally, we present quantum tomography of the prepared nonclassical and entangled mechanical states. Our result represents a concrete step towards feedback-based operation of a quantum acoustic processor.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets generated and analysed for this study are available from the corresponding author on reasonable request.
References
Pechal, M., Arrangoiz-Arriola, P. & Safavi-Naeini, A. H. Superconducting circuit quantum computing with nanomechanical resonators as storage. Quantum Sci. Technol. 4, 015006 (2018).
Hann, C. T. et al. Hardware-efficient quantum random access memory with hybrid quantum acoustic systems. Phys. Rev. Lett. 123, 250501 (2019).
Chamberland, C. et al. Building a fault-tolerant quantum computer using concatenated cat codes. PRX Quantum 3, 010329 (2022).
Satzinger, K. J. et al. Quantum control of surface acoustic-wave phonons. Nature 563, 661–665 (2018).
Chu, Y. et al. Creation and control of multi-phonon Fock states in a bulk acoustic-wave resonator. Nature 563, 666–670 (2018).
Arrangoiz-Arriola, P. et al. Resolving the energy levels of a nanomechanical oscillator. Nature 571, 537–540 (2019).
Sletten, L. R., Moores, B. A., Viennot, J. J. & Lehnert, K. W. Resolving phonon Fock states in a multimode cavity with a double-slit qubit. Phys. Rev. X 9, 021056 (2019).
Bienfait, A. et al. Phonon-mediated quantum state transfer and remote qubit entanglement. Science 364, 368–371 (2019).
Bienfait, A. et al. Quantum erasure using entangled surface acoustic phonons. Phys. Rev. X 10, 021055 (2020).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Arrangoiz-Arriola, P. & Safavi-Naeini, A. H. Engineering interactions between superconducting qubits and phononic nanostructures. Phys. Rev. A 94, 063864 (2016).
Chu, Y. et al. Quantum acoustics with superconducting qubits. Science 358, 199–202 (2017).
Chu, Y. & Gröblacher, S. A perspective on hybrid quantum opto- and electromechanical systems. Appl. Phys. Lett. 117, 150503 (2020).
Mason, D., Chen, J., Rossi, M., Tsaturyan, Y. & Schliesser, A. Continuous force and displacement measurement below the standard quantum limit. Nat. Phys. 15, 745–749 (2019).
Jiang, W. et al. Efficient bidirectional piezo-optomechanical transduction between microwave and optical frequency. Nat. Commun. 11, 1166 (2015).
Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Superconducting qubit to optical photon transduction. Nature 588, 599–603 (2020).
Jost, J. D. et al. Entangled mechanical oscillators. Nature 459, 683–685 (2009).
Ockeloen-Korppi, C. F. et al. Stabilized entanglement of massive mechanical oscillators. Nature 556, 478–482 (2018).
Riedinger, R. et al. Remote quantum entanglement between two micromechanical oscillators. Nature 556, 473–477 (2018).
Barzanjeh, S. et al. Stationary entangled radiation from micromechanical motion. Nature 570, 480–483 (2019).
de Lépinay, L. M., Ockeloen-Korppi, C. F., Woolley, M. J. & Sillanpää, M. A. Quantum mechanics–free subsystem with mechanical oscillators. Science 372, 625–629 (2021).
Kotler, S. et al. Direct observation of deterministic macroscopic entanglement. Science 372, 622–625 (2021).
Bertet, P. et al. Direct measurement of the Wigner function of a one-photon Fock state in a cavity. Phys. Rev. Lett. 89, 200402 (2002).
Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007).
Arrangoiz-Arriola, P. et al. Coupling a superconducting quantum circuit to a phononic crystal defect cavity. Phys. Rev. X 8, 031007 (2018).
MacCabe, G. S. et al. Nano-acoustic resonator with ultralong phonon lifetime. Science 370, 840–843 (2020).
Satzinger, K. J. et al. Simple non-galvanic flip-chip integration method for hybrid quantum systems. Appl. Phys. Lett. 114, 173501 (2019).
Kelly, J. Fault-Tolerant Superconducting Qubits PhD thesis, Univ. California (2015).
Wang, C. et al. Integrated high quality factor lithium niobate microdisk resonators. Opt. Express 22, 30924–30933 (2014).
Vidal-Álvarez, G., Kochhar, A. & Piazza, G. Delay lines based on a suspended thin film of X-cut lithium niobate. In 2017 IEEE Int. Ultrason. Symp. 1–4 (IEEE, 2017). https://doi.org/10.1109/ULTSYM.2017.8091845.
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Wollack, E. A. et al. Loss channels affecting lithium niobate phononic crystal resonators at cryogenic temperature. Appl. Phys. Lett. 118, 123501 (2021).
Heidler, P. et al. Non-Markovian effects of two-level systems in a niobium coaxial resonator with a single-photon lifetime of 10 milliseconds. Phys. Rev. Appl. 16, 034024 (2021).
Lachance-Quirion, D. et al. Entanglement-based single-shot detection of a single magnon with a superconducting qubit. Science 367, 425–428 (2020).
Gambetta, J. et al. Qubit-photon interactions in a cavity: measurement-induced dephasing and number splitting. Phys. Rev. A 74, 042318 (2006).
Brune, M., Haroche, S., Lefevre, V., Raimond, J. M. & Zagury, N. Quantum nondemolition measurement of small photon numbers by Rydberg-atom phase-sensitive detection. Phys. Rev. Lett. 65, 976–979 (1990).
Brune, M. et al. From Lamb shift to light shifts: vacuum and subphoton cavity fields measured by atomic phase sensitive detection. Phys. Rev. Lett. 72, 3339–3342 (1994).
Wang, Z. et al. Quantum dynamics of a few-photon parametric oscillator. Phys. Rev. X 9, 021049 (2019).
Motzoi, F., Gambetta, J. M., Rebentrost, P. & Wilhelm, F. K. Simple pulses for elimination of leakage in weakly nonlinear qubits. Phys. Rev. Lett. 103, 110501 (2009).
Chen, Z. et al. Measuring and suppressing quantum state leakage in a superconducting qubit. Phys. Rev. Lett. 116, 020501 (2016).
Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett. 106, 180504 (2011).
Córcoles, A. D. et al. Process verification of two-qubit quantum gates by randomized benchmarking. Phys. Rev. A 87, 030301 (2013).
Geerlings, K. et al. Demonstrating a driven reset protocol for a superconducting qubit. Phys. Rev. Lett. 110, 120501 (2013).
Johansson, J., Nation, P. & Nori, F. QuTiP 2: a Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 184, 1234–1240 (2013).
Grant, M. & Boyd, S. CVX: Matlab software for disciplined convex programming, version 2.1. http://cvxr.com/cvx (CVX Research, Inc., 2014).
Acknowledgements
A.-H.S.N. is indebted to S. Safavi-Naeini, M. Palizban, H. Safavi-Naeini for their support during the preparation of this manuscript. We thank M. Kang, T. P. McKenna, W. Jiang, M. Pechal, Y. P. Zhong, K. K. S. Multani, N. R. Lee, M. M. Fejer and P. J. Stas for discussions. We acknowledge the support of the David and Lucile Packard Foundation and the Sloan Research Fellowship. This work was funded by the U.S. government through the Office of Naval Research (ONR) under grant no. N00014-20-1-2422, the U.S. Department of Energy through grant no. DE-SC0019174 and the National Science Foundation CAREER award no. ECCS-1941826. E.A.W. was supported by the Department of Defense through the National Defense Science and Engineering Graduate Fellowship. A.Y.C. was supported by the Army Research Office through the Quantum Computing Graduate Research Fellowship, as well as the Stanford Graduate Fellowship. Device fabrication was performed at the Stanford Nano Shared Facilities (SNSF), supported by the National Science Foundation under award ECCS-2026822, and the Stanford Nanofabrication Facility (SNF). This work was partly funded by Amazon Web Services and NTT Research.
Author information
Authors and Affiliations
Contributions
E.A.W. and A.Y.C. designed and fabricated the device. E.A.W., A.Y.C., R.G.G. and P.A.-A. developed the fabrication process. Z.W., R.G.G. and A.H.S.-N. provided experimental and theoretical support. E.A.W. and A.Y.C. performed the experiments and analysed the data. E.A.W., A.Y.C. and A.H.S.-N. wrote the manuscript, with the other authors assisting. A.H.S.-N. supervised all efforts.
Corresponding author
Ethics declarations
Competing interests
P.A.-A. is currently a research scientist at Amazon, and A.H.S.-N. is an Amazon Scholar. The other authors declare no competing interests.
Peer review
Peer review information
Nature thanks Audrey Bienfait and the other, anonymous, reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Device images.
Angled top view (a) and angled side view (b) photographs of the fully packaged device. The top (mechanics) chip is secured face down to the bottom (qubit) chip by an adhesive polymer (9:1 ethanol to GE Varnish) applied manually to the sides of the chip.
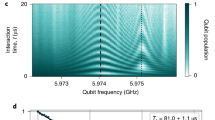
Extended Data Fig. 2 Qubit characterization.
a, Qubit spectrum as a function of the externally applied magnetic flux \({\Phi }_{{\rm{e}}}\), in units of the magnetic flux quantum Φ0. The qubit is tuned from its maximum frequency \({\omega }_{{\rm{g}}{\rm{e}}}^{max}/2\pi =2.443\,{\rm{G}}{\rm{H}}{\rm{z}}\) and shows avoided crossings at \({\omega }_{{{\rm{m}}}_{1}}/2{\rm{\pi }}=2.053\,{\rm{GHz}}\) and \({\omega }_{{{\rm{m}}}_{2}}/2{\rm{\pi }}=2.339\,{\rm{GHz}},\) corresponding to the mechanical modes M1 and M2. b, Qubit T1 as a function of qubit frequency. Each horizontal slice represents a separate ring-down measurement, with the qubit excited state probability indicated by the colour bar. The fitted T1 values for each slice are plotted as white points. c, Randomized benchmarking results. Here the qubit response is measured after applying a random sequence of Clifford gates, with the final Clifford always chosen to map the cumulative effect of the sequence to |e⟩. d, Qubit thermometry measurement. The dark blue points (dark red points) show the measurement result with (without) an initial Xπ pulse to exchange the steady-state |g⟩ and |e⟩ populations. The light blue (light red) lines show the fits for these Rabi-like oscillations, with amplitudes Ag (Ae). From these amplitudes, we estimate a qubit thermal population in |e⟩ of Pe,th = 0.057.
Extended Data Fig. 3 Swap characterization.
a, Experimental results (top) and simulated qubit excited state probability Pe (bottom) for the Rabi-swap experiment described in Fig. 2b, d. The asymmetry in the chevrons of the qubit–mechanics interaction is replicated by master equation simulations. b, Qubit state tomography results for the X (blue), Y (red) and Z (black) components of the qubit state Bloch vector during a resonant Rabi-swap experiment. The qubit is initially prepared in |e⟩ and then swapped to the upper mechanical mode M2 before performing tomography on the qubit. c, Qubit state tomography results for a resonant Rabi-swap experiment, similar to b, in which the qubit now starts in |g⟩ + |e⟩.
Extended Data Fig. 4 State reconstruction.
a, Experimental results for the mechanical displacement calibration, showing the inferred displacement amplitudes |αinf| (points) corresponding to the voltage amplitude of each applied pulse, and a fit to the hockey-stick model (line). b, Simulation and fit of the displacement calibration performed experimentally in a. A small thermal state (nth = 0.10) is displaced with a programmed amplitude (input |α|, x axis), from which we determine the inferred displacement amplitude (|αinf|, y axis). The simulation data are plotted in dark blue points, with a fit to the hockey-stick model plotted in light blue. In the linear portion of the graph, we find the ratio of these values, c1 = (inferred |α|)/(input |α|) ≃ 1, as expected. c, Results of error propagation for the reconstructed fidelity \({ {\mathcal F} }_{{\rm{s}}}\) = 0.786 ± 0.003 in single-mode tomography of the |0⟩ + |1⟩ state. d, Results of error propagation for the joint tomography Bell-state fidelity \({ {\mathcal F} }_{{\rm{Bell}}}\) = 0.66 ± 0.03.
Extended Data Fig. 5 Parity measurement.
a, Parity of the displaced mechanical state |1⟩ prepared in the upper mechanical mode. The state is prepared and characterized using the same pulse sequence as in Fig. 3a. Here we use 16 displacements in the upper-right quadrant of the complex plane and perform the Ramsey measurement for a total time tmax = 4.0 μs. For each displacement \(\hat{D}(\alpha )\), parity is computed from the extracted phonon number distribution as Π(α) = Σn=0(−1)nPα(n). The axes correspond to the complex voltage amplitudes of the applied microwave pulses that generate these displacements. This yields a minimum observed parity Π(0) ≃ −0.45 at the origin. b, The same parity measurement, plotted in terms of the inferred displacement amplitudes. We extrapolate these α values using the calibration scheme described in Extended Data Fig. 4. c, Upper-right quadrant of the reconstructed Wigner function shown in Fig. 3f, reproduced here for comparison.
Supplementary information
Rights and permissions
About this article
Cite this article
Wollack, E.A., Cleland, A.Y., Gruenke, R.G. et al. Quantum state preparation and tomography of entangled mechanical resonators. Nature 604, 463–467 (2022). https://doi.org/10.1038/s41586-022-04500-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-022-04500-y
This article is cited by
-
Engineering multimode interactions in circuit quantum acoustodynamics
Nature Physics (2024)
-
Sound interactions across multiple modes
Nature Physics (2024)
-
Surface modification and coherence in lithium niobate SAW resonators
Scientific Reports (2024)
-
Realistic prediction and engineering of high-Q modes to implement stable Fano resonances in acoustic devices
Nature Communications (2023)
-
A quantum electromechanical interface for long-lived phonons
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.