Abstract
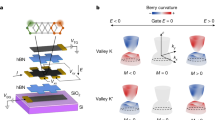
Ferromagnetism is most common in transition metal compounds where electrons occupy highly localized d orbitals. However, ferromagnetic order may also arise in low-density two-dimensional electron systems1,2,3,4,5. Here we show that gate-tuned van Hove singularities in rhombohedral trilayer graphene6 drive spontaneous ferromagnetic polarization of the electron system into one or more spin and valley flavours. Using capacitance and transport measurements, we observe a cascade of transitions tuned to the density and electronic displacement field between phases in which quantum oscillations have fourfold, twofold or onefold degeneracy, associated with a spin- and valley-degenerate normal metal, spin-polarized ‘half-metal’, and spin- and valley-polarized ‘quarter-metal’, respectively. For electron doping, the salient features of the data are well captured by a phenomenological Stoner model7 that includes valley-anisotropic interactions. For hole filling, we observe a richer phase diagram featuring a delicate interplay of broken symmetries and transitions in the Fermi surface topology. Finally, we introduce a moiré superlattice using a rotationally aligned hexagonal boron nitride substrate5,8. Remarkably, we find that the isospin order is only weakly perturbed, with the moiré potential catalysing the formation of topologically nontrivial gapped states whenever itinerant half- or quarter-metal states occur at half- or quarter-superlattice band filling. Our results show that rhombohedral graphene is an ideal platform for well-controlled tests of many-body theory, and reveal magnetism in moiré materials4,5,9,10 to be fundamentally itinerant in nature.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
Change history
15 December 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41586-021-04181-z
References
Tanatar, B. & Ceperley, D. M. Ground state of the two-dimensional electron gas. Phys. Rev. B 39, 5005–5016 (1989).
Pudalov, V. M., Kuntsevich, A. Y., Burmistrov, I. S. & Reznikov, M. Thermodynamic studies of two-dimensional correlated electron systems. J. Low Temp. Phys. 181, 99–111 (2015).
Hossain, M. S. et al. Observation of spontaneous ferromagnetism in a two-dimensional electron system. Proc. Natl Acad. Sci. USA 117, 32244–32250 (2020).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020).
Zhang, F., Sahu, B., Min, H. & MacDonald, A. H. Band structure of ABC-stacked graphene trilayers. Phys. Rev. B 82, 035409 (2010).
Stoner, E. C. Collective electron ferromagnetism. Proc. R. Soc. A 165, 372–414 (1938).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Polshyn, H. et al. Electrical switching of magnetic order in an orbital Chern insulator. Nature 588, 66–70 (2020).
Castro, E. V., Peres, N. M. R., Stauber, T. & Silva, N. A. P. Low-density ferromagnetism in biased bilayer graphene. Phys. Rev. Lett. 100, 186803 (2008).
Lee, Y. et al. Gate tunable magnetism and giant magnetoresistance in ABC-stacked few-layer graphene. Preprint at https://arxiv.org/abs/1911.04450 (2019).
Kerelsky, A. et al. Moiréless correlations in ABCA graphene. Proc. Natl Acad. Sci. USA 118, 4 (2021).
Shi, Y. et al. Electronic phase separation in multilayer rhombohedral graphite. Nature 584, 210–214 (2020).
Chen, G. et al. Signatures of tunable superconductivity in a trilayer graphene moiré superlattice. Nature 572, 215–219 (2019).
Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Negative compressibility of interacting two-dimensional electron and quasiparticle gases. Phys. Rev. Lett. 68, 674–677 (1992).
Varlet, A. et al. Anomalous sequence of quantum Hall liquids revealing a tunable Lifshitz transition in bilayer graphene. Phys. Rev. Lett. 113, 116602 (2014).
Zibrov, A. A. et al. Emergent Dirac gullies and gully-symmetry-breaking quantum Hall states in ABA trilayer graphene. Phys. Rev. Lett. 121, 167601 (2018).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Dean, C., Kim, P., Li, J. I. A. & Young, A. F. in Fractional Quantum Hall Effects: New Developments (eds Halperin, B. I. & Jain, J. K.) 317–375 (World Scientific, 2020).
Zhang, Y.-H., Mao, D., Cao, Y., Jarillo-Herrero, P. & Senthil, T. Nearly flat Chern bands in moiré superlattices. Phys. Rev. B 99, 075127 (2019).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Balents, L., Dean, C. R., Efetov, D. K. & Young, A. F. Superconductivity and strong correlations in moiré flat bands. Nat. Phys. 16, 725–733 (2020).
Masubuchi, S., Ono, M., Yoshida, K., Hirakawa, K. & Machida, T. Fabrication of graphene nanoribbon by local anodic oxidation lithography using atomic force microscope. Appl. Phys. Lett. 94 082107 (2009).
Li, H. et al. Electrode-free anodic oxidation nanolithography of low-dimensional materials. Nano Lett. 18, 8011–8015 (2018).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Zibrov, A. A. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017).
Alicea, J. & Fisher, M. P. A. Interplay between lattice-scale physics and the quantum Hall effect in graphene. Solid State Commun. 143, 504–509 (2007).
Kharitonov, M. Phase diagram for the ν = 0 quantum Hall state in monolayer graphene. Phys. Rev. B 85, 155439 (2012).
Cong, C. et al. Raman characterization of ABA- and ABC-stacked trilayer graphene. ACS Nano 5, 8760–8768 (2011).
Polshyn, H. et al. Quantitative transport measurements of fractional quantum Hall energy gaps in edgeless graphene devices. Phys. Rev. Lett. 121, 226801 (2018).
Acknowledgements
We acknowledge discussions with A. MacDonald, L. Fu, F. Wang and M. Zaletel. A.F.Y. acknowledges support from the National Science Foundation under DMR-1654186, and the Gordon and Betty Moore Foundation under award GBMF9471. We acknowledge the use of the research facilities within the California NanoSystems Institute, supported by the University of California, Santa Barbara and the University of California, Office of the President. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan (grant number JPMXP0112101001) and JSPS KAKENHI (grant numbers 19H05790 and JP20H00354). E.B. and T.H. were supported by the European Research Council under grant HQMAT (grant agreement number 817799). A.G. acknowledges support by the European Unions Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement number 754411.
Author information
Authors and Affiliations
Contributions
H.Z. and T.X. fabricated the device with assistance from E.M.S. and J.R.E. H.Z. performed the measurements, advised by A.F.Y. K.W. and T.T. grew the hBN crystals. A.G., T.H., E.B. and M.S. contributed to the theoretical interpretation and performed the numerical simulations. H.Z., A.G., M.S., E.B. and A.F.Y. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Mikito Koshino and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Sample fabrication procedure.
a, ABC-stacked domains in mechanically exfoliated trilayer graphene flakes are identified by taking the Raman spectra and extracting the peak maximum corresponding to the 2D mode32. b, ABC-stacked domains are isolated using atomic force microscope based anodic oxidation lithography27. c, The lower part of the heterostructure is assembled on a polypropylene carbonate (PPC) film which is then d, flipped as it is deposited onto the target substrate33. e, The sample is then vacuum annealed at 375 °C to remove the PPC film under the heterostructure. f, The upper part of the heterostructure, which contains the top graphite gate, trilayer graphene and hBN, is assembled separately and deposited onto the lower part of the heterostructure. g, The top hBN and top graphite gate are etched with XeF2 followed by O2 plasma to open windows on the heterostructure, allowing the stacking order to be confirmed after the manipulations of step f. h, The heterostructure is etched with CHF3 and O2 plasma and metal is deposited to form electrical contacts. i, Typical Raman spectra of ABA- and ABC-stacked trilayer graphene, centered on the 2D mode. j, Optical micrograph of the trilayer graphene flake used to fabricate Sample A. Scale bar represents 20µm. k, Raman spectrum map of the trilayer graphene flake in panel j. The color represents the peak position of the 2D mode. The scan range is indicated in black dashed line in panel j. The scale bar represents 10µm. l, Optical micrograph of partially processed Sample A. The cyan regions are where the top graphite gate and the hBN on top of it has been etched. Since the bottom gate does not overlap with the etched window, this allows inspection with Raman spectroscopy of the stacking order of the trilayer graphene. The sale bar represents 10µm. The rough location of the actual device is indicated by black dashed line. m, Raman spectrum map of the partially processed Sample A. The region surrounded by a red boundary box remains in ABC-stacking order, which later became the active device region for sample A. n, Optical micrograph of Sample A after fabrication. Scale bar represents 3µm. o, Optical micrograph of Sample B. Scale bar represents 3µm.
Extended Data Fig. 2 Measurements at low carrier density and displacement field.
a, Inverse compressibility versus carrier density and out-of-plane magnetic field near the charge neutrality point at \(D=0\). b, Zoom-in of a. c, Line-cuts of b along the direction indicated by the arrows in b. d, \({R}_{xx}\) versus carrier density and out-of-plane magnetic field near the charge neutrality point at \(D=0\). e, Zoom-in of d. f, Line-cuts of e along the direction indicated by the arrows in e. g, \({R}_{xy}\) versus carrier density and out-of-plane magnetic field near the charge neutrality point at \(D=0\). h, Zoom-in of g. i, Line-cuts of h along the direction indicated by the arrows in h.
Extended Data Fig. 3 Shubnikov de Haas oscillation at D = 0 in Sample A.
a, \({R}_{xx}\) vs ne and \({B}_{\perp }\) measured at \(D=0\). b, Fast Fourier transform of data in a, the range of \({B}_{\perp }\) chosen is 0.02T to 1T. The multiple phases are schematically represented by the Fermi contours on the top.
Extended Data Fig. 4 Shubnikov de Haas oscillation at D = 0 in Sample A.
a, b, Inverse compressibility as function of carrier density and displacement measured at \(T=5.6\)K. c, d, Inverse compressibility as a function of carrier density measured at various temperatures at \(D=0.46\) V/nm (c) and \(-0.46\) V/nm (d). Each curve is offset by 50eV\(\cdot {A}_{{\rm{u}}.{\rm{c}}.}\) for clarity.
Extended Data Fig. 5 Shubnikov de Haas oscillations in Sample A.
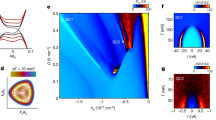
a, c, \({R}_{xx}\) vs \({B}_{\perp }\) at electron doping. The measurements are performed at \(D=-0.43\)V/nm at \({n}_{{\rm{e}}}=0.27\times {10}^{12}{{\rm{cm}}}^{-2}\) in a, \(0.54\times {10}^{12}{{\rm{cm}}}^{-2}\) in b and \(1.09\times {10}^{12}{{\rm{cm}}}^{-2}\) in c. The fast Fourier transform in Fig. 2b was calculated from these results. d, e, \({R}_{xx}\) vs ne and \({B}_{\perp }\) at hole doping. Data in panel d are measured at \(D=0.23\) V/nm. Data in panel e are measured at \(D=0.4\) V/nm. The fast Fourier transforms in Fig. 3c, d are calculated from these results.
Extended Data Fig. 6 Quantum capacitance magneto-oscillations.
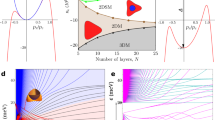
a–f, Inverse compressibility as a function of the out-of-plane magnetic field at fixed ne and D. g, h, Inverse compressibility versus the out-of-plane magnetic field and the carrier density at \(D=\) 0.34V/nm. The range of carrier density is chosen to lie within the one-fold degenerate phase in panel g and two-fold degenerate phase in panel h; in both cases no change in the degeneracy is observed in the low-\({B}_{\perp }\) limit.
Extended Data Fig. 7 In-plane magnetic field dependence of the phase boundaries.
a, κ vs ne and \({B}_{\parallel }\) at \(D=\) 0.37V/nm, which covers the phase boundary between a 4-fold degenerate phase and a 1-fold degenerate phase. b, Same as a, measured at \(D=\) 0.33V/nm, which covers a phase boundary between a 1-fold degenerate phase with a simple Fermi surface and a 1-fold degenerate phase with annular Fermi surface. c, \({R}_{xx}\) vs ne and \({B}_{\parallel }\) at \(D=\) 0.37V/nm, which covers a phase boundary between a 4-fold degenerate phase and a 2-fold degenerate phase.
Extended Data Fig. 8 Anomalous Hall effect and Magnetic hysteresis.
a, Hall resistance \({R}_{xy}\) as a function of the out-of-plane magnetic field \({B}_{\perp }\) measured at \({n}_{{\rm{e}}}=0.19\times {10}^{12}{{\rm{cm}}}^{-2}\), \(D=-0.4\) V/nm. b, Same measurement at \({n}_{{\rm{e}}}=0.43\times {10}^{12}{{\rm{cm}}}^{-2}\), \(D=0.38\) V/nm with a 0.1T in-plane magnetic field applied. The curves measured at different temperatures are offset by 200Ω for clarity. The Hall resistance was obtained by measuring the four-terminal resistance in two configurations and applying the Onsager reciprocal relation9.
Extended Data Fig. 9 Magnetic field response of the insulating states in Sample B.
a, Inverse compressibility versus carrier density and out-of-plane magnetic field at \(D=\) 0.52V/nm measured in sample B. b, Same as a, measured at \(D=\) -0.57 V/nm. c, \({R}_{xy}\) versus \({B}_{\perp }\) measured at \({n}_{{\rm{e}}}=-0.52\times {10}^{12}{{\rm{cm}}}^{-2}\), \(D=\) −0.47 V/nm.
Extended Data Fig. 10 Extended κ vs ne and D data at B = 0.
The contact resistance increases at \({n}_{{\rm{e}}} > 0\), \(D > 0\) and at \({n}_{{\rm{e}}} < 0\), \(D < 0\) due to the formation of a pn-junction near the contact, producing the defect features near the charge neutrality point.
Supplementary information
Supplementary Information
This file contains theoretical modelling, and includes Supplementary Table 1, Figs. 1–3 and additional references.
Rights and permissions
About this article
Cite this article
Zhou, H., Xie, T., Ghazaryan, A. et al. Half- and quarter-metals in rhombohedral trilayer graphene. Nature 598, 429–433 (2021). https://doi.org/10.1038/s41586-021-03938-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03938-w
This article is cited by
-
Fractional quantum anomalous Hall effect in multilayer graphene
Nature (2024)
-
Electric field tunable bandgap in twisted double trilayer graphene
npj 2D Materials and Applications (2024)
-
Rhombohedral graphene goes correlated at four or five layers
Nature Nanotechnology (2024)
-
Ferroelectric and spontaneous quantum Hall states in intrinsic rhombohedral trilayer graphene
Nature Physics (2024)
-
Probing the tunable multi-cone band structure in Bernal bilayer graphene
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.