Pauli-limit violation and re-entrant superconductivity in moiré graphene

Abstract

Moiré quantum matter has emerged as a materials platform in which correlated and topological phases can be explored with unprecedented control. Among them, magic-angle systems constructed from two or three layers of graphene have shown robust superconducting phases with unconventional characteristics^1,2,3,4,5. However, direct evidence of unconventional pairing remains to be experimentally demonstrated. Here we show that magic-angle twisted trilayer graphene exhibits superconductivity up to in-plane magnetic fields in excess of 10 T, which represents a large (2–3 times) violation of the Pauli limit for conventional spin-singlet superconductors^6,7. This is an unexpected observation for a system that is not predicted to have strong spin–orbit coupling. The Pauli-limit violation is observed over the entire superconducting phase, which indicates that it is not related to a possible pseudogap phase with large superconducting amplitude pairing. Notably, we observe re-entrant superconductivity at large magnetic fields, which is present over a narrower range of carrier densities and displacement fields. These findings suggest that the superconductivity in magic-angle twisted trilayer graphene is likely to be driven by a mechanism that results in non-spin-singlet Cooper pairs, and that the external magnetic field can cause transitions between phases with potentially different order parameters. Our results demonstrate the richness of moiré superconductivity and could lead to the design of next-generation exotic quantum matter.

Main

A recent advance in quantum materials is the capability of creating artificial moiré superlattices through the stacking of two-dimensional materials with a twist angle and/or a lattice mismatch. In certain moiré superlattices, the appearance of flat bands gives rise to various correlated phenomena^{1,2,3,4,5,8,9,10,11,12,13,14}, including correlated insulators, ferromagnetic phases, and—in particular—superconductivity. Robust superconductivity has been reproducibly found in magic-angle twisted bilayer graphene (MATBG)^1,2,3, and more recently in magic-angle twisted trilayer graphene (MATTG)^4,5. The simultaneous presence of correlated insulator or resistive states in these systems has elicited extensive interest in the origin of this unusual superconducting phase. Moreover, MATTG exhibits a unique electric displacement field tunability, and its superconducting state can be tuned into the ultra-strong coupling regime. These aspects make MATTG an attractive platform on which to investigate the nature of moiré superconductivity.

Superconductivity arises from Cooper pairing between electrons, and one fundamental question about superconductivity is its pairing symmetry—namely the spatial symmetry and the spin configuration. The former can be classified as s-wave, p-wave, d-wave or other exotic symmetries, whereas the spin configuration can be spin-singlet or spin-triplet. Most superconductors have a spin-singlet pairing, including conventional superconductors that can be described by Bardeen–Cooper–Schrieffer (BCS) theory as well as even-parity unconventional superconductors such as cuprates¹⁵. Conversely, evidence of spin-triplet superconductivity has been found in only a few systems, such as UPt₃ (ref. ¹⁶) and UTe₂ (ref. ¹⁷). Spin-triplet pairing between fermionic atoms has long been investigated in the superfluid helium-3, which exhibits a rich phase diagram that consists of different triplet phases¹⁸. Recently, additional interest in spin-triplet superconductivity has emerged because of the accompanying odd-parity spatial symmetry, which can host topological states¹⁹ that are important for fault-tolerant quantum computing. For systems in which valley degrees of freedom are present—as is the case for many moiré systems—the order parameter may possess a richer combination of spin, valley and spatial symmetries^20,21,22.

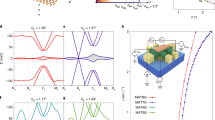
Here we perform quantum transport measurements in MATTG in the presence of a magnetic field parallel to the sample plane in order to gain insight into the spin configuration of the superconducting state. Our results indicate that MATTG is unlikely to be a spin-singlet superconductor. We fabricated high-quality MATTG devices in which the adjacent layers are sequentially twisted by θ and −θ, where θ ≈ 1.57° is the magic angle for MATTG, as detailed previously⁴ (Fig. 1a). Besides the theoretical prediction of nearly flat bands in MATTG—similar to those in MATBG²³—MATTG additionally exhibits a unique electric-field tunability⁴. The MATTG bands can be reduced to MATBG-like flat bands and a dispersive Dirac band^23,24,25,26, and the hybridization between them can be controlled by the electric displacement field D. The number of electrons per moiré unit cell, known as the moiré filling factor, is defined by ν = 4n/n_s, where n is the carrier density and ${n}_{{\rm{s}}}=\frac{8{\theta }^{2}}{\sqrt{3}{a}^{2}}$ is the superlattice density (a = 0.246 nm is the lattice constant of graphene). Figure 1b shows the longitudinal resistance R_xx, as a function of ν and D without any magnetic field, where a number of D-dependent correlated resistive states are present at integer filling factors ν = +1, ±2, +3, ±4. Superconductivity appears in the vicinity of the ν = ±2 correlated states, and the highest critical temperature T_c is found at ν = −2 − δ (δ is a fraction smaller than 1); it approaches 2.9 K at ν = −2.4 (see refs. ^4,5). The critical temperature is further tunable by varying D, and the optimal D/ε₀ that maximizes T_c is located around ±0.4–0.5 V nm⁻¹, where ε₀ is the vacuum permeability. Near optimal ν and D, the superconductivity was found to be in the ultrastrong coupling regime⁴.

Fig. 1: Superconductivity in MATTG at high in-plane magnetic fields.

a, Schematic of the experimental system. Four-probe measurements are performed by flowing current I and measuring longitudinal voltage difference V_xx and Hall voltage V_xy as shown. Top and bottom gate voltages (V_tg and V_bg, respectively) are applied to control the carrier density and electric displacement field in the sample. In-plane field B_‖ (parallel to the two-dimensional plane) and out-of-plane field B_⊥ (perpendicular to the plane) are shown. A small B_⊥ is applied to correct for a possible tilt of the sample with respect to B_‖. V_bias is the a.c. bias voltage. b, d, Longitudinal resistance R_xx at B_‖ = 0 T (b) and B_‖ = 10 T (d) at T = 300 mK. c, Voltage–current (V_xx–I) curves at different values of B_‖ at ν = −2.4, D/ε₀ = −0.44 V nm⁻¹ and T = 300 mK. Inset, magnification of the middle region shows the flatness of the V_xx–I curves at large B_‖. e, Evolution of superconductivity on the hole-doped side as a function of B_‖. Superconductivity persists up to B_‖ = 10 T.

Pauli-limit violation

In a superconductor, the application of an external magnetic field suppresses superconductivity in two main ways. One is through the formation of vortices (for type-II superconductors), which leads to loss of superconducting coherence when the average spacing between vortices is below their characteristic size ξ. However, such suppression is nearly absent when the magnetic field is parallel to the plane of an atomically thin two-dimensional superconductor. For example, the in-plane field that is required to thread one flux-quantum laterally through the MATTG unit cell is well in excess of 100 T (see Methods for a detailed estimate). Alternatively, a magnetic field can suppress superconductivity via the Zeeman effect, or through in-plane orbital effects²⁷. The Zeeman effect, in particular, imposes an upper bound on the critical magnetic field of spin-singlet superconductors, known as the Pauli (or Clogston–Chandrasekhar) limit^6,7. For weakly coupled BCS superconductors (that is, with Δ = 1.76k_BT_c, where Δ is the superconducting pairing gap and k_B is the Boltzmann constant), and for a g-factor of g = 2, this is given by B_P = 1.86 T/K×T_c. Above this field, the formation of Cooper pairs becomes energetically unfavourable. However, superconductivity above the Pauli limit can still exist in the presence of finite-momentum pairing or strong spin–orbit coupling. The former gives rise to the Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state^28,29, which can boost the critical magnetic field beyond the Pauli limit by a small amount³⁰. The latter can lead, for example, to an Ising-like type of pairing, which can boost the critical field well beyond the Pauli limit^31,32,33. For MATTG, the nominal Pauli limit at the optimal doping and displacement field is of the order of 4–5 T (assuming weak coupling and g = 2; see Methods for further discussion), depending on the selected resistance threshold.

Notably, we find that the superconductivity in MATTG at ν = −2 − δ persists even in the presence of a large parallel magnetic field B_‖ = 10 T (Fig. 1d), which is much higher than the nominal Pauli limit. Figure 1e shows the evolution of the superconducting phase in the ν–D space as a function of B_‖. At B_‖ = 10 T, a narrow region near optimal doping, ν = −2.4, remains superconducting in the range |D|/ε₀ ≤ 0.6 V nm⁻¹. In Fig. 1c, the robustness of superconductivity (that is, not a normal state with low resistance) is shown by measuring the evolution of the V_xx–I (voltage–current) curves as a function of B_‖. Although the critical current steadily decreases as B_‖ increases, it is clear that at B_‖ = 10 T, the V_xx–I plots still exhibit an extremely flat region at finite d.c. current bias—indicating zero resistance—and a sharp peak in the differential resistance dV_xx/dI at the critical current.

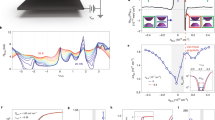
To obtain the extent of Pauli-limit violation, we investigate the multi-dimensional datasets in ν, B_‖ and T (at D/ε₀ = −0.41 V nm⁻¹). As shown in Fig. 2a, the size of the ν–T superconducting dome at −2 − δ shrinks as B_‖ is applied, where ${T}_{{\rm{c}}}^{50 \% }$ (see Methods for precise definition) at ν = −2.4 (the optimal doping) is reduced from 2.7 K to 1.35 K at B_‖ = 10 T. The resistance versus B_‖ and T at ν = −2.28 and the corresponding R_xx−T traces are shown in Fig. 2b and 2c, respectively. The constant-resistance contours in Fig. 2b correspond to roughly 10%, 20% and 30% of the normal-state R_xx at B_‖ = 0 T (see Methods), as shown in Fig. 2c. We find that the contours roughly follow the Ginzburg–Landau expression $T\propto \,1-\alpha {B}_{\parallel }^{2}$ (where α is a fitting parameter; see Methods) from T_c down to the lowest temperature, T ≈ 0.3 K (Fig. 2b). Using this formula, we can obtain the zero-temperature critical field B_c‖(0) by extrapolation, using different percentages of the normal-state R_xx to calculate T_c. At ν = −2.28, we find B_c‖(0) = 9.4 T (10% normal resistance), whereas T_c using the same threshold is 1.56 K, giving a nominal Pauli limit of B_P = 2.9 T. The Pauli violation ratio (PVR), defined as B_c‖(0)/B_P, therefore reaches 3.2 at this density.

Fig. 2: Large Pauli-limit violation in MATTG.

a, Evolution of the superconducting dome as a function of B_‖. Each colour plane shows the resistance versus ν and T at a fixed B_‖. At ν = −2.4 (optimal doping), T_c decreases to 1.35 K when B_‖ = 10 T. b, B_‖–T phase diagram at ν = −2.28. The data points denote constant-resistance contours at 10%, 20% and 30% of the zero-field normal-state resistance, and the coloured tick marks on the B_‖-axis represent the corresponding Pauli limit. The contours roughly follow the Ginzburg–Landau expression $T\propto 1-\alpha {B}_{\parallel }^{2}$ (solid curves), where α is a fitting parameter. By extrapolating the contours to zero temperature, we find the critical magnetic fields 9.41 T, 10.18 T and 10.73 T, which give consistent PVRs of 3.23, 3.27 and 3.23 for the 10%, 20% and 30% contours, respectively. c, Line cuts corresponding to b at a spacing of 1 T. d, Same as b for ν = −3. Extraction of the PVR at this density yields values of 2.37, 2.42 and 2.69, respectively, using resistance thresholds of 10%, 20% and 30%. e, PVR extracted as a function of ν for resistance thresholds of 10%, 20% and 30%. All measurements above are taken at displacement field D/ε₀ = −0.41 V nm⁻¹. The orange halo conceptually shows that the coupling strength is greatest near ν = −2.4, whereas the PVR does not have a strong dependence on ν. Extended Data Fig. 4 shows the PVR plotted against D at the optimal doping of ν = −2.4.

Figure 2e shows the PVR plotted against ν in the −2 − δ dome. Notably, the PVR is always greater than 2 over the entire range of ν in the −2 − δ superconducting dome, and extractions with different normal-state R_xx percentage thresholds give largely consistent values of the PVR (see Extended Data Fig. 1 for the electron-doped side and Extended Data Fig. 2 for other devices, the PVR values of which are also greater than 2). In particular, we find the PVR to be approximately 2.5 even when ν is close to −3, near the edge of the superconducting dome (see Fig. 2a, B_‖ = 0 slice and Fig. 2d) where ${T}_{{\rm{c}}}^{10 \% }$ < 1 K. Around this density and displacement field, the coupling strength determined by the coherence length and T_c/T_F (where T_F is the Fermi temperature) is substantially smaller⁴ than at ν = −2.28. These observations indicate that the large PVR is not directly correlated with the coupling strength, but rather is an inherent property of the superconductivity, such as its spin configuration.

Re-entrant superconductivity

We also observe additional superconducting phases at large B_‖, for a range of D values that are smaller than the optimal value. Figure 3a shows the B_‖ > 5 T region of the B_‖–T phase diagram at ν = −2.4 and D/ε₀ = −0.31 V nm⁻¹. In the low-temperature region close to the Berezinskii–Kosterlitz–Thouless (BKT) transition of the system⁴, the zero-resistance state (light blue) disappears around B_‖ = 8 T. Above 8 T, however, a zero-resistance region reappears and persists to above 10 T, signalling a re-entrant superconducting phase. On the other hand, ${T}_{{\rm{c}}}^{50 \% }$, which represents the centre of the superconducting transition, decreases monotonically with the in-plane magnetic field. Figure 3b, c shows the corresponding R_xx–T curves for different values of B_‖, in which the re-entrant superconductivity manifests as a crossing of the R_xx–T curves at T ≈ 0.6 K. We observe a similar re-entrant behaviour when examining differential resistance versus d.c. current bias at high B_‖, as shown in Fig. 3d–f. For each curve in Fig. 3e, f, the differential resistance has a large peak corresponding to the major step in the V_xx–I curve at the critical current (Fig. 1d), and multiple ‘shoulders’ at smaller I. We find re-entrant behaviour with respect to B_‖ at the first shoulder, which corresponds to a transition between a nondissipative state (dV_xx/dI = 0; light blue region in Fig. 3d) and a slightly dissipative state (dV_xx/dI > 0), whereas the position of the large dV_xx/dI  peak evolves monotonically with B_‖, analogous to the behaviour of ${T}_{{\rm{c}}}^{50 \% }$.

Fig. 3: Re-entrant superconductivity.

All data were obtained at ν = −2.4 and D/ε₀ = −0.31 V nm⁻¹. a, R_xx plotted as a function of B_‖ and T, in the B_‖ range 5–10 T. The superconducting phase present at B_‖ = 0 is suppressed around B_‖ = 8 T, and a re-entrant superconducting phase begins to appear. The re-entrant behaviour exists only in the region near zero resistance. b, c, Line cuts of R_xx plotted against T (b) and magnified view (c) at different values of B_‖, showing the non-monotonic behaviour of the R_xx–T curves near the BKT transition temperature, around the transition field of B_‖ ≈ 8 T. d, Differential resistance dV_xx/dI plotted as a function of B_‖ and I shows a similar trend to the temperature dependence, in which the re-entrant phase boundary near the critical current defines the zero resistance. e, f, Line cuts of dV_xx/dI plotted against I (e) and magnified view (f) at different values of B_‖ show similar non-monotonic behaviour as in b, c, demonstrating the re-entrant superconducting phase. Colour legends of c, f are the same as those in b, e.

Investigation of the re-entrant superconducting behaviour in the full space of ν, D and B_‖ reveals an intricate phase diagram that has multiple superconducting phases. Figure 4a shows the resistance versus B_‖–D. We denote the prominent low-field and high-field zero-resistance regions as SC-I and SC-II. At large D (|D|/ε₀ > 0.5 V nm⁻¹), SC-I directly transitions to a dissipative state as B_‖ is increased. Conversely, at intermediate D (0.3 V nm⁻¹ < |D|/ε₀ < 0.5 V nm⁻¹), we find that the boundary between SC-I and SC-II is marked by a continuous resistive ‘filament-like’ region. As D decreases, smaller islands of superconducting regions appear between 7 T and 8 T (see Methods for discussion). Figure 4b shows the density dependence of the phases at D/ε₀ = −0.24 V nm⁻¹. All of the high-field superconducting phases are visible only in the range −2.52 < ν < −2.28, close to the optimal doping ν ≈ −2.4. Figure 4c shows the temperature dependence of the transition between SC-I and SC-II. From 0.3 K to 0.6 K, a double-peak transition can be clearly observed. When the temperature is further decreased, the resistive features of the transition become weaker (see also Extended Data Fig. 3a). We performed bidirectional sweeps in B_‖ at these values of ν and D, which reveal a hysteretic behaviour and may point towards a first-order transition (see Extended Data Fig. 3b, c). Figure 4d shows the evolution of the phases as a function of T and B_‖ for different D at fixed ν = −2.4, which captures the evolution of the transition between SC-I and SC-II. We note that at D/ε₀ = −0.47 V nm⁻¹ (close to the optimal D at zero magnetic field), we cannot clearly see the onset of SC-II—perhaps because it requires magnetic fields higher than the maximum that we were able to apply. The schematic phase diagram is summarized in Fig. 4e, in which the phase boundaries of SC-I, SC-II and the transition defined by ${T}_{{\rm{c}}}^{50 \% }$ are illustrated.

Fig. 4: Field-induced transition between superconducting phases in MATTG.

a, Resistance as a function of D and B_‖ at optimal doping ν = −2.4. The measurements were performed at T = 0.4 K. SC-I and SC-II denote the zero-field superconducting phase (Fig. 2) and the high-field re-entrant phase (Fig. 3), respectively. They are clearly separated by a resistive ‘filament’. At fine-tuned displacement fields of around −0.23 V nm⁻¹ and −0.12 V nm⁻¹, we find additional regions that have lower resistance, which might signal the onset of additional phases. The dashed white line marks D/ε₀ = −0.24 V nm⁻¹; see b. b, Resistance as a function of ν and B_‖ at D/ε₀ = −0.24 V nm⁻¹ (dashed white line in a). The white dashed line here denotes the optimal doping ν = −2.4. c, Temperature dependence of the plot of R_xx against B_‖, at the values of D and ν marked by the white dashed lines in a and b. Between SC-I and SC-II, there are clearly two resistive peaks. The curves are measured when ramping down the field. A bidirectional sweep in B_‖ reveals some hysteretic behaviours, which might be suggestive of a first-order transition (see Extended Data Fig. 3). d, Evolution of the B_‖–T phase diagrams upon variation of D. The critical B_‖, at which the transition between SC-I and SC-II occurs, varies with D. e, Three-dimensional schematic of the phase diagram of the superconducting phases in the |D|–B–T space. The red and blue surfaces denote the boundaries of the SC-I and SC-II phases, respectively, and the purple surface denotes the mean-field T_c determined by 50% of the normal-state resistance.

Discussion

Our results indicate that the spin configuration of the superconducting state in MATTG is unlikely to consist of spin singlets. Although large violations of the Pauli limit have been observed for spin-singlet superconductors, these are typically due to one of the following mechanisms: First, strong spin-orbit coupling (SOC), such as in two-dimensional transition metal dichalcogenides^31,32,33. However, graphene and graphene multilayers are known for their very weak SOC, including both the intrinsic term (of the order of tens of μeV, see refs. ^34,35) as well as the Rashba term (for electric fields up to 0.8 V nm⁻¹, as we use here)³⁶. The SOC would have to be more than a factor of 30 larger (well in excess of 1.2 meV, the Zeeman splitting at 10 T) to account for the PVR values that we observe. Moreover, a violation of the Pauli limit due to SOC—as observed in TMDs—requires the breaking of inversion symmetry³⁷. However, MATTG is inversion-symmetric (at zero D) and yet we still observe a PVR of approximately ≥3 (see Extended Data Fig. 4 for the plot of PVR against D). Although we argue that all of these SOC mechanisms (see Methods for additional discussion on other possible SOC-related effects) are unlikely to account for the PVR we observe, further work is necessary to fully determine whether there is any appreciable contribution to the PVR from SOC in MATTG. Second, strongly coupled superconductors (with a large T_c/T_F ratio) can exhibit a large Δ/k_BT_c ratio, which can give rise to a large apparent ratio of B_c/T_c that exceeds the Pauli limit. In MATTG, however, the PVR does not exhibit substantial variation across the entire superconducting dome (Fig. 2e), whereas the coupling strength varies by more than an order of magnitude⁴. It is therefore unlikely that the strong-coupling mechanism accounts for the Pauli-limit violation across the entire dome. We also note that neither of the above mechanisms can account for the stabilization of the re-entrant phase at high magnetic field. Third, in a singlet superconductor, the FFLO state could be stabilized at high magnetic fields beyond the Pauli limit (at zero temperature). However, in a two-dimensional BCS superconductor, the B_c enhancement is at most around 40% above the Pauli limit³⁰—much less than the threefold violation that was observed in our experiments. Furthermore, the fact that the critical contours in the B–T phase diagrams follow quadratic behaviour from low temperature up to T_c (Fig. 2b, d) implies that even close to T_c—where an FFLO state is unlikely to form—the critical B is already much higher than the expected value for a spin-singlet BCS superconductor. Therefore, although FFLO-type physics could still be relevant for the high-field phases, it is unlikely to account for the large Pauli-limit violation in MATTG.

Given that none of the usual mechanisms that lead to Pauli-limit violation in spin-singlet superconductors are likely to have a dominant role in MATTG, it is logical to consider the possibility of a spin-triplet order parameter in MATTG. In a spin-triplet superconductor, the Cooper pairs have spin angular momentum S = 1, and the spin configuration of the order parameter can be represented by a complex vector¹⁸ d. The response of a spin-triplet state to an external field, B, crucially depends on the alignment between d and B. Neglecting orbital effects and SOC, an equal-spin pairing (ESP) state that has spins along the direction of B (d·B = 0) does not respond to the field at all, whereas a non-ESP state with d∥B is maximally suppressed by B, similar to a spin-singlet state. In magic-angle graphene systems, the additional valley degree of freedom can lead to an extra pair-breaking effect due to orbital effects, when Cooper pairs formed from electrons with opposite momenta (and thus opposite valleys) are subject to an in-plane B field²⁷. Regardless of the spin configuration, this orbital pair-breaking effect can eventually lead to the suppression of superconductivity. Therefore, the ESP triplet state might be a viable candidate as a pairing state, which can account for the large Pauli-limit violation in the low-field state (SC-I) and be eventually suppressed owing to the orbital pair-breaking effect. An alternative scenario is a spin–valley locked pairing state at zero field²⁰, which consists of a superposition of spin-singlet and spin-triplet states, and which rotates into a spin-polarized state at high magnetic field.

In addition to the large PVR, the observation of re-entrant superconducting phases provides further support for a non-spin-singlet pairing. Until now, superconductivity at high magnetic fields has most notably been identified in organic^38,39 and ferromagnetic^16,17,40 superconductors. Different mechanisms have been suggested to explain these exotic phases, including dimensional crossover³⁸, exchange stabilization³⁹ and ferromagnetic fluctuations^17,41. Compared to these systems, we note that the low-field phase and the re-entrant phase in MATTG are possibly separated by a first-order transition (see Methods and Extended Data Fig. 3), which is reminiscent of the transition between the A and B phases¹⁸ in helium-3. We also note that the re-entrant behaviour is observed only near the BKT transitions—not in the higher-temperature region in which the initial decrease in resistance occurs—which suggests that all the identified superconducting phases could correspond to the same instability that stems from the normal phase¹⁸. The change in BKT transition temperature T_BKT near the transition might then be attributed to the difference in phase stiffness. As in the case¹⁸ of superfluid helium-3, such behaviour could imply that both SC-I and SC-II are spin-triplet phases with different order parameters. As one possibility, although SC-I is the ground state at zero field, SC-II could be a spin-polarized phase (non-unitary) that is stabilized only at high magnetic fields. The presence of the additional valley degree of freedom in MATTG enables a richer set of combinations of spin, valley and spatial symmetries with a multitude of possible order parameters. The electronic states that underlie the superconductivity could be spin–valley flavour polarized as shown by recent experiments^42,43, or have a more complicated structure⁴⁴—for example, an inter-valley coherent state⁴⁵. Further investigations are required in order to determine the full pairing symmetry in the different superconducting phases of MATTG^20,21,22.

Methods

Sample fabrication

In brief, the MATTG stack is sandwiched between two hexagonal boron nitride (hBN) flakes 30–80 nm thick. The hBN and graphene flakes were first exfoliated on SiO₂/Si substrates and then screened with optical microscopy. Then we use a dry pick-up technique to fabricate the multilayer stack. A layer of poly(bisphenol A carbonate)(PC)/polydimethylsiloxane (PDMS) on a glass slide is used to sequentially pick up the flakes. The three pieces of graphene that make up MATTG are in situ laser-cut from a single graphene flake⁴⁴. The resulting stack is released on hBN on a Pd/Au stack. The Hall-bar is defined with electron beam lithography and reactive ion etching. The top gate and electrical contacts are made of Cr/Au. Further details can be found in ref. ⁴. Optical and atomic force microscopy pictures of the main MATTG device we studied are shown in Extended Data Fig. 5.

Measurement and data analysis

The electronic transport in MATTG is measured in a cryostat with base temperature of 0.25 K. We bias the sample with an a.c. current with frequency of 10 Hz, and measure the four-probe voltage with SR-830 lock-in amplifiers, synchronized at the same frequency. The current and voltage signals are first amplified by 10⁷ V/A and 1,000, respectively. Data of resistance hysteresis between SC-I and SC-II are measured using a current bias of 5 nA, whereas all other measurements are performed with a 1 nA bias. For d.c. measurements (Figs. 1c, 3d–f), we use a digital–analogue converter to provide the d.c. bias current. The d.c. voltage is measured using a digital multimeter, whereas the differential resistance dV_xx/dI is simultaneously recorded from the lock-in amplifier.

The in-plane field measurement is performed in a triple-axis vector magnet. We mounted the sample vertically so that an in-plane field up to 10 T could be applied using the Z axis of the magnet. The X axis magnet is used to compensate for the tilt of the sample (about 3°). To ensure an accurate calibration, we utilize the superconductivity in the device itself as a highly sensitive magnetometer. Essentially, for a particular in-plane field (which is applied through the Z axis of the vector magnet, B_z), we scan the perpendicular field (applied through the X axis of the vector magnet, B_x) and we record the longitudinal voltage V_xx on the sample, which is gated to the edge of the superconducting dome, where the voltage drop is just above zero. Because a perpendicular field quickly suppresses the superconductivity, the minimum in V_xx thus corresponds to a zero net perpendicular component experienced by the sample. Examples of the calibration curve are shown in Extended Data Fig. 6. We note that there is an approximately 15° angle between the B_x axis and the direction normal to the sample plane, so the net change in the perpendicular component is ΔB_⊥ ≈ ΔB_xcos15°, while the change in the in-plane component $\Delta {B}_{x}\,\sin \,15^\circ$ (maximum about 100 mT) is negligible compared to the full field applied via B_z (up to 10 T). The accuracy of this calibration is determined by how well we can determine the centre of the calibration curve, which is typically better than 5 mT. For the measurements done at a fixed in-plane field, we perform this calibration procedure before the scan. For the measurements in which the in-plane field is varied, we first perform this calibration at the lowest and the highest in-plane fields of the scan. We find out the B_x values that are necessary to compensate for those two in-plane fields, and subsequently, during the scan, we set the B_x to a value interpolated between those two values whenever the in-plane field is changed.

To further show that a small residual perpendicular component is not the cause of the SC-II phase, we measured the response of both SC-I and SC-II when an extra perpendicular field is applied via B_x, as shown in Extended Data Fig. 7a. Both SC-I and SC-II are gradually suppressed by B_⊥ as expected, indicating that the appearance of the re-entrant SC-II is not due to sample misalignment with the field axis. In particular, the non-superconducting separation between SC-I and SC-II persists at all B_⊥, indicating that SC-I and SC-II are separate superconducting phases. Extended Data Fig. 7b–e further shows Fraunhofer-like patterns at several in-plane magnetic fields. Although we did not see oscillations at zero field and optimal density and displacement field (see figure 1k in ref. ⁴), we indeed find evidence of Fraunhofer-like patterns at B_‖ = 9 T and 7 T at ν = −2.4, D/ε₀ = −0.31 V nm⁻¹, indicating that both SC-I and SC-II phases are true superconducting phases with phase-coherent properties.

For the graphics in Figs. 2b, d, 3a and Extended Data Figs. 1, 2, because the raw data were taken at non-regular temperature intervals, we first interpolated the data into a regular grid in B_‖ and T before plotting. We have checked that no artefacts are introduced by this interpolation. Raw data can be found in ref. ⁴⁶.

PVR extraction

For the PVR determination, we first extract the zero-field normal-state resistance by fitting the high-temperature part of the data with a straight line R_N(T) = aT + b, where a and b are parameters. For a given threshold p (p = 10%, 20%, 30%), we find the intersection of the zero-field resistance curve with pR_N(T). The resistance at this intersection is denoted ${R}_{{\rm{N}}}^{p}$. The intersection also defines the zero-field critical temperature ${T}_{{\rm{c}}}^{p}(0)$. The data points in Fig. 2b, d are constant-resistance contours corresponding to ${R}_{{\rm{N}}}^{10 \% }$, ${R}_{{\rm{N}}}^{20 \% }$ and ${R}_{{\rm{N}}}^{30 \% }$, respectively.

Because each contour roughly follows $T=\,{T}_{{\rm{c}}}^{p}(0)(1-{\alpha }_{p}{B}_{\parallel }^{2})$ from ${T}_{{\rm{c}}}^{p}(0)$  down to the lowest temperature we can measure, we fit the points in each contour to this formula (${\alpha }_{p}$ is a fitting parameter) and obtain the zero-temperature critical field through extrapolation, towards the point at which the contour would intercept the T = 0 axis. This is given by ${B}_{{\rm{c}}}^{p}(0)={\alpha }_{p}^{-1/2\,}$. The corresponding PVR is then calculated as PVR = ${B}_{{\rm{c}}}^{p}(0)$/(1.86 T/K × ${T}_{{\rm{c}}}^{p}(0)$). We performed this procedure independently for each ν and p = 10%, 20%, 30% and plotted the result in Fig. 2e. We find that the choice of the threshold percentage makes no qualitative difference in the extracted PVR.

Additional Pauli-limit violation data

We observed large Pauli-limit violation in other superconducting regions of the main device under study, as well as in two other devices. Extended Data Fig. 1 shows the Pauli-limit violation at representative densities and displacement fields in the ν = +2 − δ and ν = +2 + δ superconducting domes, on the electron-doping side of charge neutrality. From the 10%, 20% and 30% normal-state resistance contours, we extract critical magnetic fields ${B}_{{\rm{c}}}^{10 \% }(0)$ = 3.99 T, ${B}_{{\rm{c}}}^{20 \% }(0)$ = 4.39 T and ${B}_{{\rm{c}}}^{30 \% }(0)$ = 4.93 T for  ν = +2 − δ (Extended Data Fig. 1a), and ${B}_{{\rm{c}}}^{10 \% }(0)$ = 7.24 T, ${B}_{{\rm{c}}}^{20 \% }(0)$ = 8.31 T and ${B}_{c}^{30 \% }(0)$ = 10.45 T for ν = +2 + δ (Extended Data Fig. 1b). These values correspond to PVRs of 3.44, 2.98 and 2.83 for +2 − δ and 2.49, 2.37 and 2.65 for +2 + δ, extracted using 10%, 20% and 30%, respectively.

Extended Data Figure 2 shows the Pauli-limit violation in two other MATTG devices we measured, device B and device C (the main device shown in the main text is denoted device A). Following the same extraction procedure as above, we obtain zero-temperature critical magnetic fields ${B}_{{\rm{c}}}^{10 \% }(0)$ = 2.87 T, ${B}_{{\rm{c}}}^{20 \% }(0)$ = 3.04 T and ${B}_{c}^{30 \% }(0)$ = 3.25 T for device B (Extended Data Fig. 2a), and ${B}_{{\rm{c}}}^{10 \% }(0)$ = 3.35 T, ${B}_{{\rm{c}}}^{20 \% }(0)$ = 3.46 T and ${B}_{c}^{30 \% }(0)$ = 3.56 T for device C (Extended Data Fig. 2b). This gives PVRs of 2.13, 2.00 and 2.00 for device B, and 2.29, 2.23 and 2.19 for device C, extracted using 10%, 20% and 30%, respectively.

Combining these data, we conclude that the large Pauli-limit violation (twofold to threefold) is a universal feature in MATTG superconductivity. This suggests that the Pauli-limit violation is likely to be an intrinsic property of the superconductivity, and may point towards an unconventional spin configuration, as discussed in the main text.

Field-induced transition between SC-I and SC-II

To further investigate the nature of the transition between SC-I and SC-II phases, we performed bidirectional sweeps in B_‖ while keeping ν, D and T fixed. We find that the resistance measured while scanning up B_‖ is considerably different from the resistance measured while scanning down, showing a hysteresis. However, the behaviour seems to be very sensitive to the measurement environment and varies from scan to scan. Extended Data Fig. 3b, c shows two such scans at ν = −2.4, D/ε₀ = −0.24 V nm⁻¹ and T = 0.3 K. The only difference between the two scans is that the coaxial cables that connect from the cryostat to the lock-in amplifiers are rearranged. In the first scan, the scan-up and scan-down curves are clearly offset in B_‖. In the second scan, the peak amplitude shows a considerable difference, while no offset in B_‖ is seen. We point out that the instability shown in Extended Data Fig. 3b, c occurs only when sweeping the magnetic field up and down, while fixing temperature, density, and displacement field. The data shown in Fig. 4a, b, d, on the other hand, are taken while scanning displacement field/density as the fast axis and the magnetic field as the slow axis, from high to low fields. These measurements are fully reproducible and do not show any hysteresis.

We believe that the observation of hysteretic behaviour—as well as the extreme sensitivity to environmental disturbances—is evidence that the transition is of a first-order nature, as first-order transitions typically have accompanying hysteresis and/or instability. Common examples include the liquid–gas and liquid–solid transitions. When a system is in the instability region, it is usually very sensitive to environmental disturbances (for example, supercooled water). In our case, changing the sample cables could be slightly altering the electromagnetic noise that is coupled to the unstable superconducting state, and thus could change the hysteretic behaviour. One possible scenario is that SC-I and SC-II are of different spin-triplet order parameters, and SC-II is stabilized by a high magnetic field and separated from SC-I by a first-order transition, similar to the A and B phases in helium-3. Further studies are necessary to determine the precise nature of these phases.

We also noted that there are smaller islands in Fig. 4a between SC-I and SC-II phases. Extended Data Fig. 3d shows the same measurement performed on the positive D side, showing that although SC-I and SC-II phases are still present, the shape of the ‘filaments’ and the positions of the islands have considerably shifted in D and B_‖. These islands may indicate the onset of additional re-entrant states, which could perhaps be attributed to an admixture state of the SC-I and SC-II phases, or could also be a signature of new superconducting phases that exist only in a narrow range at finite B_‖.

PVR versus D

Extended Data Figure 4 shows the displacement field dependence of the PVR. Here the PVR represents only the extrapolated ${B}_{{\rm{c}}}^{p(0)}$ over the corresponding Pauli limit in the SC-I phase. In this extraction we have used the resistance at T = 4 K and B_‖ = 0 as the normal resistance instead of the linear fit as described above. As can be seen, the plot of PVR versus D consistently shows values greater than 2 regardless of the threshold chosen. Therefore, we can conclude that the large PVR in MATTG is ubiquitous within the superconducting dome.

In general, we find that the behaviour of the PVR is largely symmetric with respect to the sign of D. The reason we chose D = −0.41 V nm⁻¹ (near optimal displacement field) for Fig. 2 is that the re-entrant phase is not prominent below 10 T, so a well-defined PVR (for SC-I) can be extracted. For the re-entrant phase (SC-II), Fig. 3 shows D = −0.31 V nm⁻¹ as a representative displacement field, but it is clearly visible across a wide range of displacement fields, as can be seen in the cuts in Fig. 4d.

Comparison between MATBG and MATTG

We note that no detailed measurements of the Pauli limit have been performed in MATBG near optimal doping and, because the in-plane critical field is anisotropic, a finite Pauli-limit violation—between 20% and 50%—might be likely based on the preliminary data shown in ref. ²⁷. Although there are certainly many similarities between these two systems, there are still several important differences, including the presence of a pristine Dirac band in MATTG that hybridizes with the flat band upon the application of electric displacement field, and the presence of the mirror symmetry in MATTG, which is absent in MATBG. This mirror symmetry in MATTG makes the orbital in-plane effects different from those in MATBG: because the magnetic field is an axial vector, it behaves differently under mirror symmetry for the bottom-middle layers and for the middle-top layers. This might contribute to the apparently smaller violation of the Pauli limit in the bilayer case, although this mechanism needs more experimental work to be fully verified. The mirror symmetry would be broken when a displacement field is applied, or when the top and bottom twist angles are slightly different. However, if the displacement field or twist angle difference is not too large, the mirror-symmetric physical arrangement in MATTG can still offer a limited degree of protection against the in-plane magnetic field (that is, intuitively, the magnetic flux through the top two layers and the bottom two layers partially cancel), whereas in MATBG this effect is completely absent because there is no mirror symmetry.

Another possibility is that MATBG and MATTG have different superconducting order parameters due to differences in details of materials parameters (for example, bandwidth or shape of Fermi surface). Theoretically, it is known that for superconductors in which interactions have a prominent role—which is likely to be the case for both MATBG and MATTG—the spin-singlet and spin-triplet ground states are nearly degenerate (see for example, refs. ^20,47,48,49). The preferred state is then determined by the sign of a small Hund’s coupling term, and therefore it is entirely plausible in such a scenario in which MATTG adopts the triplet pairing while MATBG adopts the singlet pairing. Future experiments and theoretical work that can determine the exact order parameters for either system will be of great interest.

Estimation of in-plane critical field due to formation of vortices

In order for the in-plane field to suppress the superconductivity in MATTG by forming vortices, these vortices have to form parallel to the layers and in between the graphene layers, and the vortex spacing needs to be equal to or less than the coherence length. Because the coherence length was determined to be almost the same as interparticle distance⁴, we can set this condition as B_‖da ≈ φ₀, where d ≈ 1 nm is the thickness of MATTG, a ≈ 10 nm is the moiré wavelength in MATTG and φ₀ = h/(2e) is the superconducting flux quantum, where h is Planck’s constant and e is the elementary charge. This gives an estimate of B_‖ ≈ 200 T, which we described as ‘well above 100 T’ in the main text. Although the specific numbers may vary slightly if we included precise values, this should give the order of magnitude of the orbital effect because of the formation of in-plane vortices in MATTG.

Further discussion on the possible effect of spin-obit coupling

Whereas graphene and derived systems are known to have weak intrinsic spin–orbit coupling (up to tens of μV), as yet there is no detailed study of SOC in MATTG or MATBG specifically, and hence a more detailed discussion of its possible effects is warranted. Although SOC has been shown to enhance the Pauli limit in certain systems containing transition metals or lanthanides, it is unlikely that SOC can account for the observed Pauli-limit violation or re-entrant superconductivity in MATTG. We discuss some of the possible scenarios below.

First, the SOC in graphene systems is inherently small. The intrinsic SOC in monolayer graphene was recently measured³⁴ to be around 40 μV, and in Bernal stacked bilayer graphene it is also 40 μV at zero D, which increases to 80 μV at finite D³⁵. We note that the authors do not attribute the D dependence to an intrinsic enhancement, but rather to a proximity-induced enhancement by the substrate. In the case of MATTG, superconductivity persists at optimal doping and displacement field up to fields well in excess of 10 T. This means that the relevant spin–orbit coupling energy that would be necessary to explain the observations in MATTG would have to be greater than 1.2 meV (the Zeeman spin splitting at 10 T), which is more than a factor of 30 larger than the SOC energy scale in graphene. In that sense, if the SOC in MATTG were to be of the same order as in the above references (40–80 μV), it would indeed be negligible. It is difficult to naturally assume that SOC will be substantial in MATTG, compared to monolayer or bilayer graphene. One possible question could be whether the flat bands might enhance SOC in the system. If this was the case, the same argument should be applicable to MATBG as well, as the flat bands in MATBG are in fact flatter than those in MATTG. However, experiments so far do not show Pauli-limit violation in MATBG comparable to that in MATTG.

The enhancement of the critical magnetic field much beyond the Pauli limit through the mechanism of SOC requires an antisymmetric SOC term (analogous to the Rashba term)^37,50,51, which is present only when inversion symmetry is broken. Because MATTG is centrosymmetric (at zero displacement field), we would expect no Pauli violation at zero D. However, the PVR at zero D is around 3. Moreover, we do not observe a strong dependence of PVR with D, as shown in Extended Data Fig. 4. Conversely, by a similar argument, because MATBG does not have inversion symmetry, its critical in-plane magnetic field would have been enhanced by the antisymmetric SOC term more than in MATTG; however, this is not experimentally observed.

One remote possibility is that the top and bottom layers experience an asymmetric local chemical environment, and therefore the system could be non-centrosymmetric in a layer-specific sense. This effect is what leads to Pauli-limit violation in heavy-fermion superlattices consisting of CeCoIn₅/YbCoIn₅ layers⁵², due to the Rashba-type SOC at each interface. However, a key requirement in such a scenario is the weak interlayer coupling, because the coupling between opposite interfaces restores the inversion symmetry and the SOC term will cancel each other. In MATTG, it is known that the flat bands are a result of mirror-symmetric combination of all three layers^23,24,25,26, and the electronic states in the flat bands are highly layer-hybridized. Therefore, it is unlikely that this local interfacial symmetry breaking is responsible for an enhanced Rashba SOC and the Pauli-limit violation.

In principle, disorder and impurities can also act as centres for inversion symmetry breaking, resulting in a spin–orbit scattering mechanism (see for example, ref. ⁵³). However, we have observed the largest Pauli violation ratios in the highest quality (less disordered) device (out of three devices we measured). The other two devices, which were more disordered, had PVRs closer to 2. We also point out that disorder and impurities are also present in regular monolayer and bilayer graphene devices, but no enhanced SOC has been measured in such devices.

One more possibility that we are aware of is the effect of Van Vleck-type magnetic susceptibility, which dominates over the Pauli susceptibility in spin–orbit split Fermi surfaces and does not have a Pauli-limiting effect³⁷. Here, it is required that the SOC energy is much larger than the superconducting gap. Although the exact gap size of MATTG is unknown, a BCS estimate using T_c would be around 0.45 meV (in fact, it could be much higher than this owing to its strong coupling nature), and for the SOC energy to be much larger than this—again, there should be more than an order of magnitude enhancement compared with bare graphene values. The same reasoning as above makes this an unlikely case.

Finally, to the best of our knowledge, SOC cannot account for the re-entrant behaviour. The observation of a re-entrant phase suggests that a new phase is stabilized only at high magnetic fields. A spin-singlet state might have its critical magnetic field enhanced by SOC, but will not be further stabilized by the magnetic field. The re-entrant phase is also unlikely to be similar to the topological superconductivity created by an s-wave superconductor in contact with a semiconductor with strong SOC, where the magnetic field would first close the trivial bulk gap and reopen a topological gap. In two-dimensional systems, the combination of Rashba SOC, s-wave superconductivity and in-plane field cannot generate a gapped topological phase⁵⁴. More exotic mechanisms that involve both Rashba and Dresselhaus SOC combined with an in-plane field⁵⁵ can possibly give rise to a topological phase, but it is unlikely to occur in the present system of inversion-symmetric MATTG, because the Dresselhaus SOC term requires broken inversion symmetry as well.

In summary, the most common pathways for the SOC enhancement of the Pauli limit do not account for the Pauli-limit violation and re-entrant superconductivity observed in MATTG, whereas the spin-triplet scenario can account for these findings more naturally.

Assumptions for the Pauli limit

The Pauli limit is estimated by assuming the electron g-factor of 2 and a weak coupling strength between the electrons. Although recent electron spin resonance experiments⁵⁶ have measured the electron g-factor in monolayer graphene to be extremely close to 2, a sizable SOC could modify the g-factor. SOC typically enhances the g-factor, which would rather decrease the critical magnetic field below the Pauli limit. Moreover, due to the same argument above, if the g-factor modification due to SOC is the cause for the Pauli-limit violation, it should occur in MATBG as well, which is not experimentally observed. The g-factor can also be enhanced in strongly interacting systems^57,58,59, but again, such enhancement would show as an apparent decrease of the critical magnetic field—that is, the opposite of what we observe. Therefore, we believe that a modification of the g-factor is an unlikely cause for the observed Pauli-limit violation.

In the strongly coupled regime, the superconducting gap Δ is no longer proportional to the T_c and can greatly exceed the BCS value of 1.76k_BT_c. Because the Pauli limit is calculated on the basis of the BCS value, the critical magnetic field can therefore greatly exceed it in this case. If our observed Pauli-limit violation is due to strong coupling, the violation should be largest at the doping and displacement field with the strongest coupling. In our case, however, although the strongest coupling region is found at about ν ≈ −2.4 (ref. ⁴), the PVR is not at a maximum there but rather at ν ≈ −2.26. Furthermore, we find the Pauli limit to be also violated by more than a factor of two even in the density and displacement field regions in the weak-coupling regime (for example, near the edge of the superconducting domes, where T_BKT/T_F is an order of magnitude smaller than at optimal doping/field). Therefore, strong-coupling alone cannot explain our experimental findings.

In a different study⁶⁰, we estimated the superconducting gap Δ in MATBG by performing edge-type tunnelling spectroscopy. However, at this point the data cannot determine quantitatively to what extent the weak-coupling assumption holds in MATBG or MATTG. In ref. ⁶⁰, k_BT_c/Δ is not found to greatly exceed the BCS value, but the measurement is not meant to be interpreted at a quantitative level to give a conclusion on this, owing to limitations of the edge-type tunnelling spectroscopy that we performed. Dedicated experiments in the future using scanning tunnelling spectroscopy or planar tunnelling could help to make more quantitative estimates for the superconducting order parameter.

Possible effects of valley pair-breaking

As we noted in ref. ²⁷, an in-plane field causes pair-breaking for an inter-valley pairing state, analogous to the Zeeman effect. However, the valley pair-breaking energy is highly anisotropic and changes sign along the Fermi surface²⁷. When the spin effect is also considered (that is, for a spin-singlet inter-valley pairing state), the Zeeman effect (which is more isotropic along the Fermi surface) is boosted by the valley effect on some parts of the Fermi surface, and counteracted on other parts of it. These two effects do not directly add up or cancel one another, because their effects on the Fermi surface have different symmetries. When we consider the momentum-averaged paramagnetic limit (which is determined by the average magnetic susceptibility in the superconducting state), the total depairing effect will be typically larger than either of them (Zeeman-only or valley-only), and thus further reduce the critical magnetic field.

To see this, we consider the following toy model. We assume the Zeeman depairing energy per unit magnetic field ε_Z = 2μ₀μ_B to be independent of momentum, and the valley depairing energy, ε_V, to be dependent on the azimuthal angle of momentum θ_k. We used for this a simplified form that captures the essence of the argument (that is, captures the correct sign changes, see ref. ²⁷), ${\varepsilon }_{{\rm{V}}}(k)=\frac{[{E}^{{\rm{K}}}(k,B)\,-\,{E}^{{\rm{K}}{}^{{\prime} }}(-k,B)]}{B}={\varepsilon }_{{\rm{V}}}\,\cos \,2{\theta }_{k}$, where E^K and E^K′ are the single-particle energies of K and K′ electrons at momentum k/−k and magnetic field B. We assume that the magnetic field is pointing towards the x direction. The momentum k here is defined with respect to the mini-Brillouin zone centre. The total depairing energy per unit magnetic field for a spin-singlet inter-valley pairing state is  ${\varepsilon }_{{\rm{d}}{\rm{e}}{\rm{p}}{\rm{a}}{\rm{i}}{\rm{r}}}(k)=[{E}^{K\uparrow }(k,B)-{E}^{{K}^{{\prime} }\downarrow }(-k,B)]/B={\varepsilon }_{{\rm{Z}}}+{\varepsilon }_{{\rm{V}}}\,\cos \,2{\theta }_{k}$. The paramagnetic susceptibility in this case can be calculated as $\chi =\frac{N(0){\mu }_{B}}{2}\,{\bar{\varepsilon }}_{{\rm{depair}}}$ in analogy to the Pauli paramagnetism, where N(0) is the density of states on the Fermi surface (assumed to be constant) and ${\bar{\varepsilon }}_{{\rm{depair}}}$ is the momentum-averaged depairing energy defined as ${\bar{\varepsilon }}_{{\rm{depair}}}=\frac{1}{2{\rm{\pi }}}\int {\rm{d}}{\theta }_{k}|{\varepsilon }_{{\rm{depair}}}(k)|\,$. Note the absolute value here, because for spin paramagnetism the susceptibility at any given momentum is always positive (spins always adopt the orientation with lower energy). To find the critical magnetic field, we set the total paramagnetic energy $\frac{1}{2{\mu }_{0}^{2}}\chi {B}^{2}$  to be equal with the superconducting condensation energy F_C, which yields the critical field ${B}_{c}\,=\,2{\mu }_{0}\sqrt{\frac{{F}_{{\rm{C}}}}{{\mu }_{B}N(0){\bar{\varepsilon }}_{{\rm{depair}}}}}$.

If we set ε_V = 0, then ${\bar{\varepsilon }}_{{\rm{depair}}}={\varepsilon }_{{\rm{Z}}}$ and the above formula recovers the Pauli limit B_P. Extended Data Fig. 8 shows ${\bar{\varepsilon }}_{{\rm{depair}}}/{\varepsilon }_{{\rm{Z}}}$ as a function of ε_V/ε_Z. In this model the total pair-breaking effect is always stronger than if only the Zeeman or only the valley effect is present. Therefore, the resulting in-plane critical field B_c for such a state will be reduced from B_P (corresponding to Zeeman-only). For these reasons, we do not think that a spin-singlet inter-valley state can possibly account for the large Pauli-limit violation in our data. The Zeeman effect needs to be suppressed (which implies a spin-triplet state if there is no substantial SOC), and the valley depairing effect has to be sufficiently small, in order to account for a critical magnetic field that exceeds the Pauli limit.

Possible origin of the multiple steps in the dV _xx/dI–I curves

The dV_xx/dI–I characteristics shown in Fig. 3e exhibit several small steps before the tall dV_xx/dI peak, indicating a small increase in dissipation before the full actual switching. We do not currently have a detailed understanding of these steps, but these are often also seen in other 2D superconductors, as demonstrated in our previous work on MATBG and monolayer WTe₂ (see for example, ref. ⁶¹). Recent work on gated 2D superconductors⁶² has attributed this small dissipation to vortex flow dynamics at finite current density, indicating that it is related to 2D BKT physics, and this might also be the case also for our devices.