Abstract
Tests of quantum mechanics on a macroscopic scale require extreme control over mechanical motion and its decoherence1,2,3. Quantum control of mechanical motion has been achieved by engineering the radiation–pressure coupling between a micromechanical oscillator and the electromagnetic field in a resonator4,5,6,7. Furthermore, measurement-based feedback control relying on cavity-enhanced detection schemes has been used to cool micromechanical oscillators to their quantum ground states8. In contrast to mechanically tethered systems, optically levitated nanoparticles are particularly promising candidates for matter-wave experiments with massive objects9,10, since their trapping potential is fully controllable. Here we optically levitate a femtogram (10−15 grams) dielectric particle in cryogenic free space, which suppresses thermal effects sufficiently to make the measurement backaction the dominant decoherence mechanism. With an efficient quantum measurement, we exert quantum control over the dynamics of the particle. We cool its centre-of-mass motion by measurement-based feedback to an average occupancy of 0.65 motional quanta, corresponding to a state purity of 0.43. The absence of an optical resonator and its bandwidth limitations holds promise to transfer the full quantum control available for electromagnetic fields to a mechanical system. Together with the fact that the optical trapping potential is highly controllable, our experimental platform offers a route to investigating quantum mechanics at macroscopic scales11.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Zurek, W. H. Decoherence and the transition from quantum to classical — revisited. In Quantum Decoherence: Poincaré Seminar 2005 (eds Duplantier, B. et al.) 1–31 (Birkhäuser, 2007).
Chen, Y. Macroscopic quantum mechanics: theory and experimental concepts of optomechanics. J. Phys. B 46, 104001 (2013).
Hornberger, K., Gerlich, S., Haslinger, P., Nimmrichter, S. & Arndt, M. Colloquium: Quantum interference of clusters and molecules. Rev. Mod. Phys. 84, 157–173 (2012).
Teufel, J. D. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011).
Chan, J. et al. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 478, 89–92 (2011).
Qiu, L., Shomroni, I., Seidler, P. & Kippenberg, T. J. Laser cooling of a nanomechanical oscillator to its zero-point energy. Phys. Rev. Lett. 124, 173601 (2020).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Rossi, M., Mason, D., Chen, J., Tsaturyan, Y. & Schliesser, A. Measurement-based quantum control of mechanical motion. Nature 563, 53–58 (2018).
Chang, D. E. et al. Cavity opto-mechanics using an optically levitated nanosphere. Proc. Natl Acad. Sci. USA 107, 1005–1010 (2010).
Romero-Isart, O., Juan, M. L., Quidant, R. & Cirac, J. I. Toward quantum superposition of living organisms. New J. Phys. 12, 033015 (2010).
Leggett, A. J. Testing the limits of quantum mechanics: motivation, state of play, prospects. J. Phys. Condens. Matter 14, R415 (2002).
Braginskii, V. B. & Manukin, A. B. Measurement of Weak Forces in Physics Experiments (Univ. of Chicago Press, 1977).
Andrews, R. W. et al. Bidirectional and efficient conversion between microwave and optical light. Nat. Phys. 10, 321–326 (2014).
Bagci, T. et al. Optical detection of radio waves through a nanomechanical transducer. Nature 507, 81–85 (2014).
Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Superconducting qubit to optical photon transduction. Nature 588, 599–603 (2020).
Cirac, J. I., Lewenstein, M., Mølmer, K. & Zoller, P. Quantum superposition states of Bose-Einstein condensates. Phys. Rev. A 57, 1208–1218 (1998).
Bose, S., Jacobs, K. & Knight, P. L. Scheme to probe the decoherence of a macroscopic object. Phys. Rev. A 59, 3204–3210 (1999).
Marshall, W., Simon, C., Penrose, R. & Bouwmeester, D. Towards quantum superpositions of a mirror. Phys. Rev. Lett. 91, 130401 (2003).
Romero-Isart, O. Quantum superposition of massive objects and collapse models. Phys. Rev. A 84, 052121 (2011).
Ashkin, A. & Dziedzic, J. M. Feedback stabilization of optically levitated particles. Appl. Phys. Lett. 30, 202 (1977).
Hebestreit, E., Frimmer, M., Reimann, R. & Novotny, L. Sensing Static forces with free-falling nanoparticles. Phys. Rev. Lett. 121, 063602 (2018).
Purdy, T. P., Peterson, R. W. & Regal, C. A. Observation of radiation pressure shot noise on a macroscopic object. Science 339, 801–804 (2013).
Jain, V. et al. Direct measurement of photon recoil from a levitated nanoparticle. Phys. Rev. Lett. 116, 243601 (2016).
Kaltenbaek, R. et al. Macroscopic quantum resonators (MAQRO). Exp. Astron. 34, 123–164 (2012).
Kiesel, N. et al. Cavity cooling of an optically levitated submicron particle. Proc. Natl Acad. Sci. USA 110, 14180–14185 (2013).
Windey, D. et al. Cavity-based 3D cooling of a levitated nanoparticle via coherent scattering. Phys. Rev. Lett. 122, 123601 (2019).
Delić, U. et al. Cavity cooling of a levitated nanosphere by coherent scattering. Phys. Rev. Lett. 122, 123602 (2019).
Delić, U. et al. Cooling of a levitated nanoparticle to the motional quantum ground state. Science 367, 892–895 (2020).
Li, T., Kheifets, S. & Raizen, M. G. Millikelvin cooling of an optically trapped microsphere in vacuum. Nat. Phys. 7, 527–530 (2011).
Gieseler, J., Deutsch, B., Quidant, R. & Novotny, L. Subkelvin parametric feedback cooling of a laser-trapped nanoparticle. Phys. Rev. Lett. 109, 103603 (2012).
Tebbenjohanns, F., Frimmer, M., Militaru, A., Jain, V. & Novotny, L. Cold damping of an optically levitated nanoparticle to microkelvin temperatures. Phys. Rev. Lett. 122, 223601 (2019).
Mancini, S., Vitali, D. & Tombesi, P. Optomechanical cooling of a macroscopic oscillator by homodyne feedback. Phys. Rev. Lett. 80, 688 (1998).
Wilson, D. et al. Measurement-based control of a mechanical oscillator at its thermal decoherence rate. Nature 524, 325–329 (2015).
Cohadon, P. F., Heidmann, A. & Pinard, M. Cooling of a mirror by radiation pressure. Phys. Rev. Lett. 83, 3174–3177 (1999).
Poggio, M., Degen, C. L., Mamin, H. J. & Rugar, D. Feedback cooling of a cantilever’s fundamental mode below 5 mK. Phys. Rev. Lett. 99, 017201 (2007).
Tebbenjohanns, F., Frimmer, M., Jain, V., Windey, D. & Novotny, L. Motional sideband asymmetry of a nanoparticle optically levitated in free space. Phys. Rev. Lett. 124, 013603 (2020).
Tebbenjohanns, F., Frimmer, M. & Novotny, L. Optimal position detection of a dipolar scatterer in a focused field. Phys. Rev. A 100, 043821 (2019).
Millen, J., Fonseca, P. Z. G., Mavrogordatos, T., Monteiro, T. S. & Barker, P. F. Cavity cooling a single charged levitated nanosphere. Phys. Rev. Lett. 114, 123602 (2015).
Clerk, A. A., Devoret, M. H., Girvin, S. M., Marquardt, F. & Schoelkopf, R. J. Introduction to quantum noise, measurement, and amplification. Rev. Mod. Phys. 82, 1155–1208 (2010).
Safavi-Naeini, A. H. et al. Observation of quantum motion of a nanomechanical resonator. Phys. Rev. Lett. 108, 033602 (2012).
Purdy, T. P., Grutter, K. E., Srinivasan, K. & Taylor, J. M. Quantum correlations from a room-temperature optomechanical cavity. Science 356, 1265–1268 (2017).
Shkarin, A. B. et al. Quantum optomechanics in a liquid. Phys. Rev. Lett. 122, 153601 (2019).
Wiseman, H. M. & Milburn, G. J. Quantum Measurement and Control (Cambridge Univ. Press, 2010).
Sudhir, V. et al. Appearance and disappearance of quantum correlations in measurement-based feedback control of a mechanical oscillator. Phys. Rev. X 7, 011001 (2017).
Sayrin, C. et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 477, 73–77 (2011).
Vijay, R. et al. Stabilizing Rabi oscillations in a superconducting qubit using quantum feedback. Nature 490, 77–80 (2012).
Magrini, L. et al. Real-time optimal quantum control of mechanical motion at room temperature. Nature https://doi.org/10.1038/s41586-021-03602-3 (2021).
Meng, C., Brawley, G. A., Bennett, J. S., Vanner, M. R. & Bowen, W. P. Mechanical squeezing via fast continuous measurement. Phys. Rev. Lett. 125, 043604 (2020).
Vanner, M. R. et al. Pulsed quantum optomechanics. Proc. Natl Acad. Sci. USA 108, 16182 (2011).
Gabrielse, G. et al. Thousandfold improvement in the measured antiproton mass. Phys. Rev. Lett. 65, 1317–1320 (1990).
Bateman, J., Nimmrichter, S., Hornberger, K. & Ulbricht, H. Near-field interferometry of a free-falling nanoparticle from a point-like source. Nat. Commun. 5, 4788 (2014).
Doherty, A. C., Tan, S. M., Parkins, A. S. & Walls, D. F. State determination in continuous measurement. Phys. Rev. A 60, 2380–2392 (1999).
Micke, P. et al. Closed-cycle, low-vibration 4 K cryostat for ion traps and other applications. Rev. Sci. Instrum. 90, 065104 (2019).
Frimmer, M. et al. Controlling the net charge on a nanoparticle optically levitated in vacuum. Phys. Rev. A 95, 061801 (2017).
Ahn, J. et al. Optically levitated nanodumbbell torsion balance and GHz nanomechanical rotor. Phys. Rev. Lett. 121, 033603 (2018).
Hebestreit, E. et al. Calibration and energy measurement of optically levitated nanoparticle sensors. Rev. Sci. Instrum. 89, 033111 (2018).
van der Laan, F. et al. Optically levitated rotor at its thermal limit of frequency stability. Phys. Rev. A 102, 013505 (2020).
Underwood, M. et al. Measurement of the motional sidebands of a nanogram-scale oscillator in the quantum regime. Phys. Rev. A 92, 061801(R) (2015).
Doherty, A. C. & Jacobs, K. Feedback control of quantum systems using continuous state estimation. Phys. Rev. A 60, 2700–2711 (1999).
Genes, C., Vitali, D., Tombesi, P., Gigan, S. & Aspelmeyer, M. Ground-state cooling of a micromechanical oscillator: Comparing cold damping and cavity-assisted cooling schemes. Phys. Rev. A 77, 033804 (2008).
Pluchar, C. M., Agrawal, A. R., Schenk, E. & Wilson, D. J. Towards cavity-free ground-state cooling of an acoustic-frequency silicon nitride membrane. Appl. Opt. 59, G107–G111 (2020).
Iwasaki, M. et al. Electric feedback cooling of single charged nanoparticles in an optical trap. Phys. Rev. A 99, 051401 (2019).
Conangla, G. P. et al. Optimal feedback cooling of a charged levitated nanoparticle with adaptive control. Phys. Rev. Lett. 122, 223602 (2019).
Kamba, M., Kiuchi, H., Yotsuya, T. & Aikawa, K. Recoil-limited feedback cooling of single nanoparticles near the ground state in an optical lattice. Phys. Rev. A 103, L051701 (2021).
Rodenburg, B., Neukirch, L. P., Vamivakas, A. N. & Bhattacharya, M. Quantum model of cooling and force sensing with an optically trapped nanoparticle. Optica 3, 318–323 (2016).
Wieczorek, W. et al. Optimal state estimation for cavity optomechanical systems. Phys. Rev. Lett. 114, 223601 (2015).
Garbini, J. L., Bruland, K. J., Dougherty, W. M. & Sidles, J. A. Optimal control of force microscope cantilevers. I. Controller design. J. Appl. Phys. 80, 1951–1958 (1996).
Acknowledgements
This research was supported by the Swiss National Science Foundation (SNF) through the NCCR-QSIT programme (grant no. 51NF40-160591) and the R’Equip programme (grant no. 206021-189605), and by the European Union’s Horizon 2020 research and innovation programme under grant no. 863132 (iQLev). We are grateful to F. van der Laan for his contributions to the particle characterization procedure. We thank O. Wipfli and C. Fischer for their suggestions in designing the cryogenic vacuum chamber, J. Piotrowski and D. Windey for their advice with the trap assembly, and Y. Li for her work on the control software. We thank our colleagues P. Back, E. Bonvin, J. Gao, A. Militaru, R. Reimann, J. Vijayan and J. Zielinska for input and discussions.
Author information
Authors and Affiliations
Contributions
F.T., M.L.M. and M.R. conducted the experiments and co-wrote the manuscript with M.F., who directed the project with L.N.
Corresponding author
Additional information
Competing interests The authors declare no competing interests.
Peer review information Nature thanks Dalziel Wilson and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
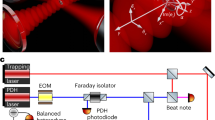
Extended Data Fig. 1 Experimental setup.
We optically trap a nanoparticle inside a cryogenic vacuum chamber using a telecom laser. In the forwards direction, we employ a libration and position detection system. In the backwards direction, we place both a homodyne and a heterodyne photodetector. AOM, acousto-optic modulator; DAQ, data acquisition card; EOM, electro-optic modulator; λ/2, half-wave plate; LO, local oscillator; PBS, polarizing beam-splitter; R, reflection; T, transmission.
Extended Data Fig. 2 Postselecting the data.
The compression cycles of the cryocooler are visible in our interferometric signal at baseband (idc[t] in grey). We identify the cycles (red dotted lines) and postselect 300-ms-long intervals (indicator function in orange) of the time traces containing the particle motion (exemplary for ihom[t] in blue).
Extended Data Fig. 3 Transfer function of the electronic feedback chain.
a, b, Measured magnitude (a) and phase (b) response of the experimentally used delay filter. The dotted, dashed, and dot-dashed vertical lines mark the location of the resonance frequency of motion along the z, x, and y axes, respectively.
Extended Data Fig. 4 Detection noise characterization.
Variance of the laser noise as a function of local oscillator power in homodyne detection. The variance, expressed in dB, is normalized to the variance of the electronic noise floor of the detector (grey). The dotted blue line provides a guide for the eye for the linear dependence between variance and power of the beam.
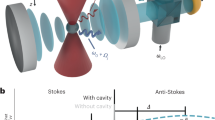
Extended Data Fig. 5 Sideband asymmetry in out-of-loop heterodyne measurements.
a, b, Stokes (a) and anti-Stokes (b) sidebands, at different electronic feedback gains, normalized to the estimated background level (grey line). Each sideband pair is simultaneously fitted to a theoretical model. c, Mechanical occupations (green squares) at different feedback gains. The black solid line is a theoretical model based on an ideal delay filter with parameters estimated from the in-loop spectra. The error bars are obtained by propagating the fit uncertainties (1 s.d.) of the areas.
Extended Data Fig. 6 Sideband cross-correlations in out-of-loop heterodyne measurements.
a, b, Real (a) and imaginary (b) parts of cross-spectra, at different electronic feedback gains. Each pair is simultaneously fitted to a theoretical model and the results are shown as black lines. The grey line marks the zero as a reference. c, d, Fitted mechanical resonance frequency (c) and effective linewidth (d) at different electronic gains. e, Extracted mechanical occupations as a function of fitted effective linewidths. The black line is a theoretical model based on an ideal delay filter and on parameters estimated from the in-loop spectra. The error bars are obtained by the fit uncertainties (1 s.d.).
Extended Data Fig. 7 Fit results.
a, Reference displacement spectrum measured by the homodyne detector at the smallest feedback gain, with a fit to a model (black line). In light red we show the spectral features excluded from the fits. b, Fitted feedback gain, γeff, as a function of the experimentally tunable electronic gain gel. Coloured dots come from fitting the corresponding spectra shown in Fig. 3a. The black squares are the full-width at half-maximum extracted from the computed actual displacement spectra. The grey line is a guide for the eye, and represents the expected linear relation.
Supplementary information
Rights and permissions
About this article
Cite this article
Tebbenjohanns, F., Mattana, M.L., Rossi, M. et al. Quantum control of a nanoparticle optically levitated in cryogenic free space. Nature 595, 378–382 (2021). https://doi.org/10.1038/s41586-021-03617-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03617-w
This article is cited by
-
Real-time two-axis control of a spin qubit
Nature Communications (2024)
-
Cavity-mediated long-range interactions in levitated optomechanics
Nature Physics (2024)
-
Acoustic frequency atomic spin oscillator in the quantum regime
Nature Communications (2023)
-
Nonlinear multi-frequency phonon lasers with active levitated optomechanics
Nature Physics (2023)
-
Time-of-flight quantum tomography of an atom in an optical tweezer
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.