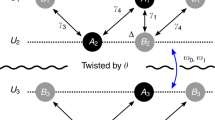
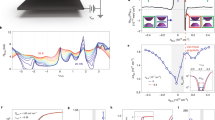
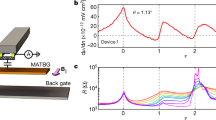
Abstract
In condensed-matter systems, higher temperatures typically disfavour ordered phases, leading to an upper critical temperature for magnetism, superconductivity and other phenomena. An exception is the Pomeranchuk effect in 3He, in which the liquid ground state freezes upon increasing the temperature1, owing to the large entropy of the paramagnetic solid phase. Here we show that a similar mechanism describes the finite-temperature dynamics of spin and valley isospins in magic-angle twisted bilayer graphene2. Notably, a resistivity peak appears at high temperatures near a superlattice filling factor of −1, despite no signs of a commensurate correlated phase appearing in the low-temperature limit. Tilted-field magnetotransport and thermodynamic measurements of the in-plane magnetic moment show that the resistivity peak is connected to a finite-field magnetic phase transition3 at which the system develops finite isospin polarization. These data are suggestive of a Pomeranchuk-type mechanism, in which the entropy of disordered isospin moments in the ferromagnetic phase stabilizes the phase relative to an isospin-unpolarized Fermi liquid phase at higher temperatures. We find the entropy, in units of Boltzmann’s constant, to be of the order of unity per unit cell area, with a measurable fraction that is suppressed by an in-plane magnetic field consistent with a contribution from disordered spins. In contrast to 3He, however, no discontinuities are observed in the thermodynamic quantities across this transition. Our findings imply a small isospin stiffness4,5, with implications for the nature of finite-temperature electron transport6,7,8, as well as for the mechanisms underlying isospin ordering and superconductivity9,10 in twisted bilayer graphene and related systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Pomeranchuk, I. On the theory of liquid 3-He. Zh. Eksp. Teor. Fiz 20, 919–926 (1950).
Andrei, E. Y. & MacDonald, A. H. Graphene bilayers with a twist. Nat. Mater. 19, 1265–1275 (2020); correction https://doi.org/10.1038/s41563-020-00917-w (2021).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Wu, F. & Sarma, S. D. Collective excitations of quantum anomalous Hall ferromagnets in twisted bilayer graphene. Phys. Rev. Lett. 124, 046403 (2020).
Khalaf, E., Chatterjee, S., Bultinck, N., Zaletel, M. P. & Vishwanath, A. Charged skyrmions and topological origin of superconductivity in magic-angle graphene. Preprint at https://arxiv.org/abs/2004.00638 (2020).
Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).
He, M. et al. Tunable correlation-driven symmetry breaking in twisted double bilayer graphene. Nat. Phys. 17, 26–30 (2021).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Saito, Y., Ge, J., Watanabe, K., Taniguchi, T. & Young, A. F. Independent superconductors and correlated insulators in twisted bilayer graphene. Nat. Phys. 16, 926–930 (2020).
Stepanov, P. et al. Untying the insulating and superconducting orders in magic-angle graphene. Nature 583, 375–378 (2020).
Arora, H. S. et al. Superconductivity in metallic twisted bilayer graphene stabilized by WSe2. Nature 583, 379–384 (2020).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Tschirhart, C. L. et al. Imaging orbital ferromagnetism in a moiré Chern insulator. Preprint at https://arxiv.org/abs/2006.08053 (2020).
Dodaro, J. F., Kivelson, S. A., Schattner, Y., Sun, X. Q. & Wang, C. Phases of a phenomenological model of twisted bilayer graphene. Phys. Rev. B 98, 075154 (2018).
Wu, F., MacDonald, A. H. & Martin, I. Theory of phonon-mediated superconductivity in twisted bilayer graphene. Phys. Rev. Lett. 121, 257001 (2018).
Lian, B., Wang, Z. & Bernevig, B. A. Twisted bilayer graphene: a phonon-driven superconductor. Phys. Rev. Lett. 122, 257002 (2019).
Martin, I. Moiré superconductivity. Ann. Phys. 417, 168118 (2020).
Wu, F., Hwang, E. & Das Sarma, S. Phonon-induced giant linear-in-T resistivity in magic-angle twisted bilayer graphene: ordinary strangeness and exotic superconductivity. Phys. Rev. B 99, 165112 (2019).
Saito, Y. et al. Hofstadter subband ferromagnetism and symmetry-broken Chern insulators in twisted bilayer graphene. Nat. Phys. https://doi.org/s41567-020-01129-4 (2021).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Xie, M. & MacDonald, A. H. Weak-field Hall resistivity and spin/valley flavor-symmetry breaking in MAtBG. Preprint at https://arxiv.org/abs/2010.07928 (2020).
Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators and topological flat-bands in magic-angle twisted bilayer graphene. Preprint at https://arxiv.org/abs/2007.03735 (2020).
Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Liu, X. et al. Tuning electron correlation in magic-angle twisted bilayer graphene using Coulomb screening. Preprint at https://arxiv.org/abs/2003.11072 (2020).
Lee, K. et al. Chemical potential and quantum Hall ferromagnetism in bilayer graphene. Science 345, 58–61 (2014).
Yang, F. et al. Experimental determination of the energy per particle in partially filled Landau levels. Preprint at https://arxiv.org/abs/2008.05466 (2020).
Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Flavour Hund’s coupling, Chern gaps and charge diffusivity in moiré graphene. Nature https://www.nature.com/articles/10.1038/s41586-021-03366-w (2021).
Bultinck, N. et al. Ground state and hidden symmetry of magic-angle graphene at even integer filling. Phys. Rev. X 10, 031034 (2020).
Khalaf, E., Bultinck, N., Vishwanath, A. & Zaletel, M. P. Soft modes in magic-angle twisted bilayer graphene. Preprint at https://arxiv.org/abs/2009.14827 (2020).
Kumar, A., Xie, M. & MacDonald, A. H. Lattice collective modes from a continuum model of magic-angle twisted bilayer graphene. Preprint at https://arxiv.org/abs/2010.05946 (2020).
Bernevig, B. et al. TBG V. Exact analytic many-body excitations in twisted bilayer graphene Coulomb Hamiltonians: charge gap, Goldstone modes and absence of Cooper pairing. Preprint at https://arxiv.org/abs/2009.14200 (2020).
Vafek, O. & Kang, J. Renormalization group study of hidden symmetry in twisted bilayer graphene with Coulomb interactions. Phys. Rev. Lett. 125, 257602 (2020).
Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Acknowledgements
We acknowledge discussions with S. Kivelson, A. Macdonald, B. Spivak and M. Zaletel, as well as experimental assistance from H. Polshyn and C. Tschirhart. Y.S. acknowledges the support of the Elings Prize Fellowship from the California NanoSystems Institute at University of California, Santa Barbara. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and the CREST (JPMJCR15F3), JST. Transport and fabrication experiments at UCSB were supported by the ARO under MURI W911NF-16-1-0361. Thermodynamic measurements were supported by the National Science Foundation under DMR-1654186. A.F.Y. acknowledges the support of the David and Lucille Packard Foundation under award 2016-65145. E.B. was supported by the European Research Council (ERC) under grant HQMAT (grant number 817799), and by the US–Israel Binational Science Foundation (BSF) under the NSF–BSF DMR programme (grant number DMR-1608055). X.L. and J.I.A.L. are supported by Brown University.
Author information
Authors and Affiliations
Contributions
Y.S., J.G. and X.L. fabricated tBLG devices. Y.S. and F.Y. performed the measurements. Y.S., F.Y. and A.F.Y. analysed the data. A.F.Y. and E.B. constructed the thermodynamic model. Y.S., F.Y., E.B. and A.F.Y. wrote the paper with input from J.I.A.L. T.T. and K.W. grew the hBN crystals.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Xuan Gao, Emanuel Tutuc and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 tBLG devices.
a, b, Top, optical images of device 1 (a) and device 2 (b). Scale bars correspond to 5 μm. Bottom, schematic of the tBLG heterostructures for device 1 (a) and device 2 (b).
Extended Data Fig. 2 Temperature dependence of the resistivity ρxx.
a, b, d, e, ρxx as a function of the nominal filling factor ν0 at various temperatures up to 30 K in device 1 (a, linear scale; b, logarithmic scale) and device 2 (d, linear scale; e, logarithmic scale). The traces in a, b are measured at T = 1.5, 5, 8, 12, 17, 22 and 30 K and the traces in d, e are measured at T = 1.7, 5, 10, 15, 20, 25 and 30 K. c, f, Two-dimensional map of ρxx as a function of ν0 and T in device 1 (c) and device 2 (f).
Extended Data Fig. 3 Temperature dependence of the Hall density behaviour.
a, c, The Hall density νH expressed in electrons per superlattice unit cell as a function of ν0 up to 20 K at a fixed B⊥ = 0.5 T. The data of device 1 are measured with T = 0.5, 2.5, 4.5, 8 and 20 K (a) and the data of device 2 are measured with T = 1.7, 4.3, 6, 10 and 20 K (c). b, d, Subtracted Hall density νH − ν0 as a function of ν0 at each temperature in device 1 (b) and device 2 (d). Insets, d(νH − ν0)/dν0 as a function of ν0 at each temperature around ν0 = −1. d(νH − ν0)/dν0 is calculated from νH − ν0 using a 20-point moving average (b) and a 40-point moving average (d) in ν0.
Extended Data Fig. 4 In-plane magnetic field dependence of the Hall density in device 1.
a, b, Hall density νH (a) and subtracted Hall density νH − ν0 (b) expressed in electrons per superlattice unit cell, and measured with Btot = 0.5, 3, 6, 9 and 12 T and fixed B⊥ = 0.5 T. c, νH − ν0 as a function of Btot and ν0 with the magnetic field applied at an angle θB = 20.5°, measured at a nominal T = 20 mK. Blue and pink circles correspond to the positions of peaks of ρxx and the points of maximum descent in νH − ν0, respectively, and denote phase boundaries between symmetry-breaking isospin ferromagnets (IF1, IF2 and IF3) and an isospin unpolarized state (IU).
Extended Data Fig. 5 Landau fan diagram at the hole side in a tilted magnetic field in device 1.
a, ρxx as a function of ν0 and total magnetic field Btot oriented at an angle with respect to the plane θB of 4.1°(a), 9.6°(b) and 20.5°(c). d–f, Schematics of the Landau fan diagram based on a–c, respectively. The numbered labels denote the Bloch band filling index, which encodes the number of electrons bound to each lattice unit cell.
Extended Data Fig. 6 Thermodynamic measurements in device 2.
a, Chemical potential μ as a function of ν0 at T = 4.2 K and B∥ = 0, 3, 6 and 9 T. b, μ as a function of ν0 at B = 0 T and T = 4.2, 12 and 20 K. c, Inverse compressibility dμ/dν as a function of ν0 at T = 4.2 K and B∥ = 0, 3, 6 and 9 T. d, dμ/dν as a function of ν0 at B = 0 T and T = 4.2, 12 and 20 K. e, dμ/dB∥ as a function of ν0 at T = 4.2 K, calculated from (μ(9 T) − μ(6 T))/3 T, (μ(6 T) − μ(3 T))/3 T and (μ(3 T) − μ(0 T))/3 T. f, dμ/dT as a function of ν0, calculated from (μ(12 K) − μ(4.2 K))/7.8 K at B∥ = 0, 3 and 6 T.
Extended Data Fig. 7 High-temperature transport in a tilted magnetic field in device 1.
a–d, ρxx (top) and d(νH − ν0)/dν0 (bottom) as a function of ν0 at T = 5 K (a), 10 K (b), 15 K (c) and 20 K (d) at Btot = 3, 6, 9, 12 and 15 T, oriented at an angle of 9.1° relative to the plane. d(νH − ν0)/dν0 is calculated from νH − ν0 using a 20-point moving average in ν0.
Extended Data Fig. 8 Temperature and in-plane magnetic field dependence of resistive peak around ν0 = +1 in device 2.
a, ρxx as a function of nominal filling factor ν0 around ν0 = +1 between 1.7 and 30 K in device 2. b, The ρxx peak position as a function of ν0 and T. c, ρxx as a function of nominal filling factor ν0 around ν0 = +1 at B∥ = 0, 3, 6, 9 and 12 T. d, The ρxx peak position as a function of ν0 and B∥.
Extended Data Fig. 9 Temperature-dependent chemical potential and resistance in device 2.
a, Chemical potential μ as a function of ν0 at 4.2, 8.0, 12, 16, 20, 26, 32, 40, 59, 76 and 96 K. dμ/dν0 in Fig. 4 is calculated by the derivative of these data. b, Inverse electronic compressibility dμ/dν as a function of ν0 at 4.2, 8, 12, 16, 20, 26, 32, 40, 59, 76 and 96 K. c, ρxx as a function of ν0 at 4.3, 8.0, 12, 16, 20, 26, 31, 40, 59, 76 and 96 K.
Extended Data Fig. 10 Entropy change per superlattice unit cell ΔS/kB from the transport data.
White triangles and black circles are phase boundaries for the Zeeman-tuned transition (\({E}_{{\rm{Z}}}^{* }/{k}_{{\rm{B}}}\)) and temperature-tuned transition (T*), respectively, determined by the ρxx peak near ν = −1. The pink curve is Δs/kB as a function of ν0, determined by equation (7).
Supplementary information
Supplementary Information
This file contains Supplementary Information on error bar eestimation and Supplementary Figures 1-7.
Rights and permissions
About this article
Cite this article
Saito, Y., Yang, F., Ge, J. et al. Isospin Pomeranchuk effect in twisted bilayer graphene. Nature 592, 220–224 (2021). https://doi.org/10.1038/s41586-021-03409-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03409-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.