Abstract
Quasi-periodic eruptions (QPEs) are very-high-amplitude bursts of X-ray radiation recurring every few hours and originating near the central supermassive black holes of galactic nuclei1,2. It is currently unknown what triggers these events, how long they last and how they are connected to the physical properties of the inner accretion flows. Previously, only two such sources were known, found either serendipitously or in archival data1,2, with emission lines in their optical spectra classifying their nuclei as hosting an actively accreting supermassive black hole3,4. Here we report observations of QPEs in two further galaxies, obtained with a blind and systematic search of half of the X-ray sky. The optical spectra of these galaxies show no signature of black hole activity, indicating that a pre-existing accretion flow that is typical of active galactic nuclei is not required to trigger these events. Indeed, the periods, amplitudes and profiles of the QPEs reported here are inconsistent with current models that invoke radiation-pressure-driven instabilities in the accretion disk5,6,7,8,9. Instead, QPEs might be driven by an orbiting compact object. Furthermore, their observed properties require the mass of the secondary object to be much smaller than that of the main body10, and future X-ray observations may constrain possible changes in their period owing to orbital evolution. This model could make QPEs a viable candidate for the electromagnetic counterparts of so-called extreme-mass-ratio inspirals11,12,13, with considerable implications for multi-messenger astrophysics and cosmology14,15.
Similar content being viewed by others
Main
Given its large collecting area and blind survey strategy, the eROSITA instrument on the Spectrum-Roentgen-Gamma (SRG) space observatory16 is capable of systematic searches for X-ray sources that are variable on timescales of hours to months (see Methods for more details). This applies to QPEs, which thus far have only been detected in X-rays1,2. The first QPE observed by eROSITA, hereafter eRO-QPE1, showed high-amplitude X-ray variability within just a few hours. It showed a strong X-ray signal in two eROSITA survey scans that were preceded, separated and followed by scans in which the signal was much fainter (Fig. 1a). Similar to the two previously known QPE sources—GSN 0691 and RX J1301.9+27472—the X-ray spectrum is very soft with most of the counts originating from below approximately 1.5–2 keV and consistent with a thermal black-body emission. As with the light curve, the spectrum shows oscillations from a faint to a bright phase (Fig. 1b). We identify eRO-QPE1 as originating within the nucleus of the galaxy 2MASS 02314715-1020112, for which we measured a spectroscopic redshift of z = 0.0505 (see Methods section ‘The host galaxies of the QPEs’). The related eROSITA quiescence (1σ upper limit) and peak intrinsic 0.5–2-keV luminosities are <2.1 × 1041 erg s−1 and approximately 9.4 × 1042 erg s−1, respectively, if the X-ray spectra are modelled with a standard accretion disk model (see Methods section ‘X-ray spectral analysis’).
a, eROSITA light curve in the 0.2–0.6-keV and 0.6–2.3-keV energy bands (circles and squares, respectively), with red and orange highlighting faint and bright observations, respectively. The start of the light curve teRO,0 is approximately MJD 58864.843 (MJD, modified Julian date), observed during the first eROSITA all-sky survey (eRASS1). b, eROSITA X-ray spectra of the bright and faint states in orange and red, as in a. c, Background-subtracted XMM-Newton X-ray light curves with 500-s bins for the European Photon Imaging Camera (EPIC) instruments: EPIC-pn (dark grey), MOS1 (green) and MOS2 (red) in the energy band shown in the legend. The beginning of both observations was contaminated by flares in the background and excluded; the dark grey solid line and contours show the underlying ≤1-keV EPIC-pn light curve to give a zeroth-order extrapolation of the rate, excluding the presence of obvious soft X-ray eruptions. tXMM,0 corresponds to the start of the cleaned MOS2 exposure in the first observation, approximately MJD 59057.805. XMM-Newton optical and UV fluxes are shown in the lower panels (units of erg cm−2 s−1, where Fλ is the spectral flux density and λ is the wavelength in angstroms), with non-detections shown as upper limits. d, Background-subtracted NICER-XTI light curve. The mean (and dispersion-on) rise-to-decay duration is approximately 7.6 h (~1.0 h) and the peak-to-peak separation is approximately 18.5 h (~2.7 h). All uncertainties are 1σ, shown as error bars or shaded regions.
Two follow-up observations triggered with the XMM-Newton X-ray telescope confirmed the remarkable bursting nature of the source (Fig. 1c, d). The first observation (hereafter eRO-QPE1-XMM1) found the source in a faint state for approximately 30 ks, followed by a sequence of three consecutive asymmetric bursts, possibly partially overlapping (Fig. 1c), which is behaviour that has not been previously observed in QPEs1,2. In terms of intrinsic 0.5–2-keV luminosity, after an initial quiescent phase at about 2.3 × 1040 erg s−1 the first burst was characterized by a fast rise and slower decay lasting around 30 ks and peaking at approximately 3.3 × 1042 erg s−1; it was then followed by a second fainter burst (peak at approximately 7.9 × 1041 erg s−1) and by a third, which was the brightest (peak at approximately 2.0 × 1043 erg s−1) but was only caught during its rise. The second XMM-Newton observation (hereafter eRO-QPE1-XMM2) showed an eruption very similar to the first seen in eRO-QPE1-XMM1 in terms of amplitude and luminosity, although lasting for >40 ks, that is, for almost as much as the three in eRO-QPE1-XMM1 combined (Fig. 1c). To better characterize the physics and to determine the duty cycle of these eruptions, we started an intense monitoring campaign with the NICER X-ray instrument aboard the International Space Station (ISS), which revealed 15 eruptions in about 11 days (Fig. 1d).
The second eROSITA QPE we have detected, hereafter eRO-QPE2, showed similar variability patterns and X-ray spectra as eRO-QPE1 during the X-ray sky survey (Fig. 2a, b). We associated it with the galaxy 2MASX J02344872-4419325 and determined a spectroscopic redshift of z = 0.0175 (see Methods section ‘The host galaxies of the QPEs’). The related intrinsic 0.5–2-keV luminosities of the quiescent (1σ upper limit) and peak phases are <4.0 × 1040 erg s−1 and approximately 1.0 × 1042 erg s−1, respectively. A follow-up observation with XMM-Newton revealed nine eruptions in a single day, oscillating between approximately 1.2 × 1041 erg s−1 and 1.2 × 1042 erg s−1 in the 0.5–2-keV band (Fig. 2c). In neither eRO-QPE1 nor eRO-QPE2 is there evidence of simultaneous optical/UV variability (see Figs. 1c, 2c), in agreement with the behaviour of GSN 0691.
a, b, As in Fig. 1a, b, for eRO-QPE2. The start of the eROSITA light curve is approximately MJD 59023.191. c, As in Fig. 1c, for the XMM-Newton observation of eRO-QPE2. tXMM,1 corresponds to the start of the cleaned MOS1 exposure, approximately MJD 59067.846. The mean (and related dispersion) of the rise-to-decay duration is about 27 min (~3 min), with a peak-to-peak separation of approximately 2.4 h (~5 min). All uncertainties are 1σ, shown as error bars or shaded regions.
eRO-QPE1 shows a distribution of QPE rise-to-decay durations with a mean (dispersion) of approximately 7.6 h (~1.0 h) and a distribution of peak-to-peak separations of about 18.5 h (~2.7 h), as derived from the NICER light curve (Fig. 1d). The duty cycle (mean duration over mean separation) is approximately 41%. Conversely, eRO-QPE2 shows much narrower and more frequent eruptions (see Fig. 2c): the mean (dispersion) of the rise-to-decay duration is approximately 27 min (~3 min), with a peak-to-peak separation of approximately 2.4 h (~5 min) and a duty cycle of around 19%. Interestingly, compared to the two previously known QPEs1,2, eRO-QPE1 and eRO-QPE2 extend the parameter space of QPE widths and recurrence times towards longer and shorter timescales, respectively. We also note that eRO-QPE1 is the most luminous and the most distant QPE discovered so far, and the most extreme in terms of timescales. The duration and recurrence times of the bursts in eRO-QPE1 are approximately an order of magnitude longer than in eRO-QPE2. This could simply be an effect of the timescales scaling with black hole mass17. We estimated the total stellar mass of the two host galaxies and that of eRO-QPE1 is 4–8 times higher than that of eRO-QPE2. Assuming a standard scaling of the black hole mass with stellar mass (see Methods section ‘The host galaxies of the QPEs’), this is broadly in agreement with their different X-ray timing properties. Furthermore, peak soft X-ray luminosities of approximately 2 × 1043 erg s−1 and 1042 erg s−1 for eRO-QPE1 and eRO-QPE2, respectively, exclude a stellar-mass black hole origin, and their X-ray positions, within uncertainties, suggest a nuclear origin (Extended Data Figs. 1a, 2a).
The optical counterparts of eRO-QPE1 and eRO-QPE2 are local low-mass galaxies with no canonical active galactic nuclei (AGN)-like broad emission lines in the optical nor any infrared photometric excess indicating the presence of hot dust (the so-called torus)18. In this sense they are similar to GSN 0693 and RX J1301.9+27474, although their optical spectra show narrow emission lines with clear AGN-driven ionization3,4. Instead, the optical counterpart of eRO-QPE1 is easily classified as a passive galaxy from the absence of emission lines (Extended Data Fig. 1b), and in eRO-QPE2 the strong narrow emission lines that are observed classify it as a star-forming galaxy (Extended Data Fig. 2b and Methods section ‘The host galaxies of the QPEs’). This in turn suggests that the two galaxies reported here have not been active for approximately at least the last 103–104 years, assuming narrow-line region light-travel timescales19. Although the number of known QPEs is too low to reach firm statistical conclusions, our blind search is inherently designed to sample the population of the QPEs’ host galaxies without bias, as opposed to serendipitous or archival discoveries, which rely on the source being previously active and known1,2. These results hint that perhaps the parent population of QPE hosts consists of more passive galaxies than active galaxies. The X-ray spectra of the QPEs in quiescence are consistent with an almost featureless accretion disk model1,2 (see Methods section ‘X-ray spectral analysis’), although the inactive nature of the host galaxies of our sources argues against a pre-existing AGN-like accretion system.
A few scenarios to explain the QPEs have been suggested1,10, some based on the presumed active nature of the host black holes of the QPEs. These include so-called limit-cycle radiation-pressure accretion instabilities (see Methods section ‘On accretion flow instabilities’), proposed for GSN 0691 based on the similarities between its observed properties and two extremely variable stellar-mass black holes, namely GRS 1915+10520,21 and IGR J17091-362422. However, the observed properties of the two QPEs reported here, as well as those of RX J1301.9+27472, are inconsistent with the theoretical predictions of this scenario5,6,7,8,9. In particular, the faster rise and slower decay of eRO-QPE1 would imply a thicker flow in the cold and stable phase than in the hot and unstable phase, contrary to theory6. Moreover, the theory predicts that once the period, the duty cycle and the luminosity amplitude are known, only specific values of black hole mass MBH and viscosity parameter α are allowed8: for eRO-QPE1 (eRO-QPE2) one solution is found for MBH ≈ 4 × 106M☉ (M☉, solar mass) and α ≈ 5 (MBH ≈ 3 × 106M☉ and α ≈ 3), therefore for the expected masses1,2 an unphysically high viscosity parameter would be required. Alternatively, more reasonable values of α ≈ 0.1 and 0.01 would yield very small MBH ≈ 2.4 × 103M☉ and MBH ≈ 60M☉ (MBH ≈ 4.3 × 103M☉ and MBH ≈ 30M☉) for eRO-QPE1 (eRO-QPE2). Even in this latter scenario and pushing α as high as approximately 0.2, the resulting thermal timescales for eRO-QPE1 (eRO-QPE2) are τth ≈ 20 s (35 s) at 20rg (rg = GMBH/c2, where G is the gravitational constant and c the speed of light in vacuum), which is orders of magnitude smaller than the observed QPE timescales (more details in Methods section ‘On accretion flow instabilities’).
Extreme or sinusoidal quasi-periodic variability as seen in QPEs is also typically associated with compact object binaries, a scenario which would not require the galactic nuclei to be previously active, as our present evidence suggests. Drawing a simplistic scenario, we assumed the mass of the main body to be in the range of approximately 104M☉–107M☉ for both eRO-QPE1 and eRO-QPE2 and computed the expected period decrease of a compact binary due to emission of gravitational waves. We inferred that a supermassive black hole binary with a mass ratio of the order of unity23 is unlikely given the properties of the observed optical, ultraviolet (UV), infrared and X-ray emission in QPEs and the lack of evident periodicity and/or strong period decrease therein. If QPEs are triggered by the presence of a secondary orbiting body, our data suggest its mass (M2) to be much smaller than the main body. This is in agreement with at least one proposed scenario for the origin of GSN 069, for which the average luminosity in a QPE cycle can be reproduced by a periodic mass-inflow rate from a white dwarf orbiting the black hole with a highly eccentric orbit10. Our current data for eRO-QPE1 only exclude M2 larger than approximately 106M☉ (~104M☉) for zero (high, ~0.9) eccentricity (as a function of the mass of the main body, Extended Data Fig. 7a); instead, for eRO-QPE2 we can already argue that only an orbiting M2 lower than approximately 104M☉ (~10M☉) is allowed for zero (~0.9) eccentricity (Extended Data Fig. 7b). More details are reported in Methods section ‘On the presence of an orbiting body’.
Future X-ray observations on longer temporal baselines (months or years) will help to constrain or rule out this scenario and to monitor the possible orbital evolution of the system. This picture is also reminiscent of a suggested formation channel of extreme-mass-ratio inspirals24,25 and it could make QPEs their electromagnetic messenger13,26. Regardless of their origin, the QPEs seen so far seem to be found in relatively low-mass supermassive black holes (~105M☉–107M☉) and finding more will help us to understand how black holes are activated in low-mass galaxies, which—although so far a poorly explored mass range in their co-evolution history27,28—is crucial for synergies with future Laser Interferometer Space Antenna (LISA) gravitational wave signals29.
a, b, Median light curve profile (with related 16th and 84th percentile contours) for eRO-QPE1 (a) and eRO-QPE2 (b), folded at the eruption peaks (see Methods).
Methods
Blind search for QPEs with eROSITA
eROSITA16 is the main instrument aboard the Spectrum-Roentgen-Gamma (SRG) mission (R. Sunyaev et al., manuscript in preparation), which was launched on 13 July 2019. On 13 December 2019 it started the first of eight all-sky surveys (eRASS1–eRASS8), each completed in six months, observing in the 0.2–8-keV band. In each survey, as the field of view moves every point of the sky is observed for ~40 s every ~4 h with the number of times (typically six) varying with the location in the sky, increasing towards high ecliptic latitudes. Our search for QPE candidates starts with a systematic screening of all eROSITA light curves, produced for each detected source on a weekly basis by the eROSITA Science Analysis Software (eSASS; H. Brunner et al., manuscript in preparation). Light curves are binned to yield one data point for each 4-h revolution (called an ‘eROday’). A light curve generated by the eSASS pipeline will trigger a ‘QPE alert’ if it shows two or more high-count states with (at least) one low-count state in between (see Figs. 1a, 2a as examples) in any of its standard energy bands (0.2–0.6 keV, 0.6–2.3 keV, 2.3–5.0 keV). As thresholds, we fixed a relative count-rate ratio (including uncertainties) of 5 if both high and low states are detected, or 3 if the low-count state is consistent with the background. Since neither the survey scans nor QPEs are strictly periodic, every eRASS can be treated as an independent sky to find new candidates. This produces a census of X-ray sources varying on hour-long timescales for each eRASS, albeit only for the specific intermittent pattern described above. Unsurprisingly, the vast majority of the automatically generated alerts are produced by Galactic sources (mainly flaring coronally active stars), but we can filter them out by finding the multi-wavelength counterpart associated with every X-ray source (M. Salvato et al., manuscript in preparation). Good QPE candidates are then selected by screening the handful of alerts with a secure or possible extra-galactic counterpart. Thanks to this process, we identified the two best eROSITA QPE candidates that were worth immediate follow-up, promptly obtained with both XMM-Newton and, in one case, NICER. Given the success of our initial search over the first nine months of the survey, we are confident that we can detect up to around 3–4 good eROSITA QPE candidates every year. Therefore, by the end of the last eROSITA all-sky survey in December 2023 this search may provide a sample of up to approximately 10–15 QPEs.
The two eROSITA QPEs
The first QPE, here named eRO-QPE1, is eRASSU J023147.2-102010, located at the astrometrically corrected X-ray position of RAJ2000, dec.J2000 = (02:31:47.26, −10:20:10.31), with a total 1σ positional uncertainty of ~2.1″. It was observed ten times between 16 and 18 January 2020 during eRASS1 with 339 s of total exposure. Using the Bayesian cross-matching algorithm NWAY30, we associated eRO-QPE1 with the galaxy 2MASS 02314715-1020112 at RAJ2000, dec.J2000 = (02:31:47.15, −10:20:11.22). The second QPE, here named eRO-QPE2, is eRASSU J023448.9-441931, located at the astrometrically corrected X-ray position of RAJ2000, dec.J2000 = (02:34:48.97, −44:19:31.65), with a total positional uncertainty of ~3.2″. It was observed 11 times between 23 and 24 June 2020 during eRASS2. It was associated via the same method30 with 2MASX J02344872-4419325, a galaxy at RAJ2000, dec.J2000 = (02:34:48.69, −44:19:32.72). Both galaxies are in the DESI Legacy Imaging Surveys31 DR8 footprint (Extended Data Figs. 1a, 2a). X-ray XMM-Newton positions were corrected with the ‘eposcorr’ task cross-correlating the sources in the X-ray image with external optical and infrared catalogues. The counterpart of the QPE itself was excluded from the cross-correlation to obtain a more unbiased estimate of the possible offset from the nucleus. The XMM-Newton X-ray positions are consistent with the nuclei of these galaxies. We took optical spectra of both galaxies with the Southern African Large Telescope (SALT)32 and measured spectroscopic redshifts of 0.0505 and 0.0175 for eRO-QPE1 and eRO-QPE2, respectively (Extended Data Figs. 1b, 2b). More details are shown in Methods sections ‘Data reduction’ and ‘The host galaxies of the QPEs’.
Previous X-ray activity
eRO-QPE1 has not previously been detected in X-rays, although upper limits can be obtained from the XMM-Newton upper limits server for ROSAT33, both from the survey and a pointed observation (taken in 1991 and 1992, with ~270 s and ~5,300 s, respectively), and the XMM-Newton Slew Survey34 (taken in 2004, 2007, 2008 and 2017, all between ~3 s and ~8 s of exposure). The ROSAT pointed observation puts a stringent upper limit at ≤3.8 × 10−14 cgs (cgs, erg s−1 cm−2) in the 0.2–2.0-keV band. However, given the very short exposures compared with the timescales of eRO-QPE1, we cannot rule out that QPEs were already ongoing and that all previous missions caught eRO-QPE1in a faint state. As with eRO-QPE1, eRO-QPE2 has not been previously detected in X-rays. Upper limits were again computed for ROSAT (taken in 1990, ~480 s of exposure) and the XMM-Newton Slew survey (taken in 2004, 2008, 2012 and 2013, all between ~4 s and ~8 s). The most stringent upper limit, at ≤8.8 × 10−14 cgs in the 0.2–2.0-keV band, comes from ROSAT. It is slightly below the flux observed by XMM-Newton in quiescence in the same band (Extended Data Fig. 4), perhaps indicating that the QPE behaviour only started more recently. For both QPE sources however, the ROSAT and Slew exposures are much shorter than the evolving timescales (the QPE quasi-period and its dispersion), hence they do not provide meaningful constraints on the start of the QPE behaviour.
Data reduction
In this section we report details of the processing of the complete dataset. We show a summary of the observations in Extended Data Table 1.
eROSITA
Members of the German eROSITA consortium (eROSITA-DE) have full and immediate access to survey data at Galactic longitudes 180° < l <360°. These data were processed using eSASS v946 (H. Brunner et al., manuscript in preparation). For eRO-QPE1 (eRO-QPE2), photons were extracted choosing a circular aperture of radius 80″ (67″), and background counts were extracted from an annulus (off-centre circle) of inner and outer radii 178″ (382″) and 996″, respectively, excluding all the other sources detected within the area. eRO-QPE1 was detected with a detection likelihood of 440 and a total number of 119 counts in the 0.2–5.0-keV band. eRO-QPE2 was detected with a detection likelihood of 125 and a total number of 48 counts in the 0.2–5.0-keV band.
XMM-Newton
XMM-Newton data from EPIC MOS1, MOS235 and EPIC-pn36 cameras and the Optical Monitor (OM)37 were processed using standard tools (SAS v. 18.0.0 and HEAsoft v. 6.25) and procedures. Event files from EPIC cameras were filtered for flaring particle background. Source (background) regions were extracted within a circle of 38″ and 34″ in eRO-QPE1 and eRO-QPE2, respectively, centred on the source (in a source-free region). eRO-QPE1 was consecutively observed three times with the U filter, then seven times with UVW1 and nine (eight) times with the UVM2 in the first (second) XMM-Newton observation, each exposure ~4,400-s long. The source was detected only in the U and UVW1 with mean magnitudes ~19.9 and ~20.3 in both XMM-Newton observations (OM light curves in Fig. 1c). eRO-QPE2 was consecutively observed twice with the U filter, then ten times with UVW1, six with UVM2 and three with UVW2; all exposures were 4,400 s. It was almost always detected in all filters with mean magnitudes of ~17.4, ~17.5, ~18.0 and ~18.1, for U, UVW1, UVM2 and UVW2 filters, respectively (OM light curves in Fig. 2c). eRO-QPE2 was flagged as extended in the U, UVW1 and UVM2 filters, and therefore the reported absolute magnitudes include at least some contamination from the host galaxy.
NICER
NICER’s X-ray Timing Instrument (XTI)38,39 onboard the ISS observed eRO-QPE1 between 17 August 2020 and 31 August 2020. Beginning late on 19 August, high-cadence observations were performed during almost every ISS orbit, which is roughly 93 min. All the data were processed using the standard NICER Data Analysis Software (NICERDAS) task ‘nicerl2’. Good time intervals (GTIs) were chosen with standard defaults, yielding ~186 ks of exposure time. We further divided the GTIs into intervals of 128 s, and on this basis we extracted the spectra and applied the ‘3C50’ model (R.R. et al., submitted) to determine the background spectra. The light curve for eRO-QPE1 in soft X-rays (Fig. 1d) was determined by integrating the background-subtracted spectrum for each 128-s GTI over the range 0.3–1.0 keV. More detailed spectral analyses of these data will be discussed in a follow-up paper.
SALT
Optical spectra of eRO-QPE1 and eRO-QPE2 were obtained using the Robert Stobie Spectrograph (RSS)40 on the Southern African Large Telescope (SALT)32 in September 2020 on the nights of the 24th and the 8th, respectively. The PG900 VPH grating was used to obtain pairs of exposures (900 s and 500 s, respectively) at different grating angles, allowing for a total wavelength coverage of 3,500–7,400 Å. The spectra were reduced using the PySALT package, a PyRAF-based software package for SALT data reductions41, which includes gain and amplifier cross-talk corrections, bias subtraction, amplifier mosaicing, and cosmetic corrections. The individual spectra were then extracted using standard Image Reduction and Analysis Facility (IRAF) procedures, wavelength calibration (with a calibration lamp exposure taken immediately after the science spectra), background subtraction and extraction of one-dimensional spectra. We could only obtain relative flux calibrations, from observing spectrophotometric standards in twilight, owing to the SALT design, which has a time-varying, asymmetric and underfilled entrance pupil42.
X-ray spectral analysis
In this work, X-ray spectral analysis was performed using v3.4.2 of the Bayesian X-ray Analysis software (BXA)43, which connects a nested sampling algorithm (UltraNest44; J.B., manuscript in preparation) with a fitting environment. For the latter, we used XSPEC v12.10.145 with its Python-oriented interface pyXSPEC. eROSITA source-plus-background spectra were fitted including a model component for the background, which was determined via a principal component analysis from a large sample of eROSITA background spectra46 (J.B. et al., manuscript in preparation). XMM-Newton EPIC-pn spectra were instead fitted using wstat, namely the XSPEC implementation of the Cash statistic47, given the good count statistics in both source and background spectra. We quote, unless otherwise stated, median values with the related 16th and 84th percentiles and upper limits at 1σ. Results are also reported in Extended Data Tables 2, 3.
eRO-QPE1
For eRO-QPE1, both eROSITA and XMM-Newton EPIC-pn spectra were fitted with a simple absorbed black body (using the models tbabs48 and zbbody) or accretion disk (tbabs and diskbb49), with absorption frozen at the Galactic equivalent hydrogen column density (NH) of NH ≈ 2.23 × 1020 cm−2, as reported by the HI4PI Collaboration50. For eROSITA, we jointly extracted and analysed spectra of the faint states (red points in Fig. 1a) and, separately, of the two bright states observed in eRASS1 (orange points in Fig. 1a). In the eROSITA bright states the temperature, in terms of kBT (kB, Boltzmann’s constant; T, temperature) in eV, is \({138}_{131}^{146}\,{\rm{eV}}\) and \({180}_{168}^{195}\,{\rm{eV}}\), using zbbody and diskbb as source models, respectively. The related unabsorbed rest-frame 0.5–2.0-keV fluxes are \({1.6}_{1.4}^{1.8}\times {10}^{-12}\,{\rm{cgs}}\) and \({1.5}_{1.4}^{1.7}\times {10}^{-12}\,{\rm{cgs}}\), respectively. The eROSITA spectrum of the faint states combined is consistent with background, with the temperature and unabsorbed rest-frame 0.5–2.0-keV flux constrained to be ≤124 eV (≤160 eV) and ≤3.5 × 10−14 cgs (≤3.4 × 10−14 cgs) for zbbody (diskbb). We also analysed the observations of eRO-QPE1 obtained six months later during eRASS2, which triggered our QPE search again: two bright states were observed separated by several faint ones, with fluxes consistent with eRASS1.
We performed time-resolved X-ray spectral analysis on XMM-Newton data, extracting a spectrum in each 500-s time bin of the EPIC-pn light curve, with the exception of the quiescence spectrum, which was extracted and analysed combining all the related time bins of both observations (that is, before t ≈ 26,500 s in eRO-QPE1-XMM1 and before t ≈ 35,788 s in eRO-QPE1-XMM2, with times as defined in Fig. 1c). Fit results obtained using XMM-Newton EPIC-pn spectra with diskbb as the source model component are shown in Extended Data Fig. 3. Furthermore, we show for visualization three EPIC-pn spectra and related best-fit models (Extended Data Fig. 5a) corresponding to the quiescence phase and the peak of both XMM-Newton observations. A more thorough X-ray spectral analysis with other models and additional components for the bright phase will be presented in future work.
eRO-QPE2
For eRO-QPE2, eROSITA’s faint and bright phases were also separately combined and analysed (Fig. 2a, b). The faint state as observed by eROSITA is consistent with background. The temperature and normalization of the source cannot be constrained, thus we only quote an upper limit for the unabsorbed rest-frame 0.5–2.0-keV flux of ≤1.9 × 10−14 cgs (≤5.7 × 10−14 cgs) using zbbody (diskbb). The spectrum of the eROSITA bright states constrains the temperature to \({164}_{149}^{182}\,{\rm{eV}}\) and at \({209}_{185}^{241}\,{\rm{eV}}\), using zbbody and diskbb as source models, respectively. The related unabsorbed rest-frame 0.5–2.0-keV fluxes are \({1.4}_{1.2}^{1.8}\times {10}^{-12}\,{\rm{cgs}}\) and \({1.5}_{1.2}^{1.8}\times {10}^{-12}\,{\rm{cgs}}\), respectively. The triggering eROSITA observation was obtained during eRASS2, although a single bright state (thus not satisfying our trigger criterion) was also detected in eRASS1 with the same flux level. For eRO-QPE2, in addition to the Galactic column density (NH ≈ 1.66 × 1020 cm−2)50 we included an absorption component at the redshift of the host galaxy (that is, with the models tbabs, ztbabs, and zbbody or diskbb). This excess absorption was inferred to be present on the basis of the XMM-Newton spectrum (see below).
For XMM-Newton, we performed time-resolved X-ray spectral analysis for each 150-s time bin of the EPIC-pn light curve. The absorption, in addition to the Galactic value, was first fitted in the XMM-Newton quiescence spectrum, which was extracted combining all the low states in the XMM-Newton light curve (Fig. 2c, Extended Data Fig. 4). The fit yielded \({N}_{{\rm{H}}}={0.35}_{0.30}^{0.40}\times {10}^{22}\,{{\rm{cm}}}^{-2}\). In all other observations, including all eROSITA spectra and the rises, peaks and decays in the XMM-Newton light curve, the additional NH was left free to vary between the 10th and 90th percentile of the fitted posterior distribution of the quiescent spectrum. Under the assumption that absorption did not vary throughout the observation, this ensures that no spurious effects are imprinted on the fit temperature and normalizations owing to degeneracies with NH; at the same time, in this way parameters are marginalized over a reasonable range in NH. Freezing the value instead would artificially narrow the uncertainties on the temperature and normalizations. Fit results obtained with diskbb as the source model are shown in Extended Data Fig. 4. Furthermore, we show for visualization the EPIC-pn spectra and best-fit models of the quiescence and peak phases (Extended Data Fig. 5b). Similar results are obtained using zbbody as the source model.
Timing analysis
In Fig. 3 we show the median (with related 16th and 84th percentile contours) light-curve profiles obtained by folding the light curve at the eruption peaks. First, a random representative burst is selected and cross-correlated with the whole light curve. The peaks of this cross-correlation identify the times when the phase is zero. Data are then folded at these phase-zero times to obtain a template median profile, which is then used to repeat the same operation and yield Fig. 3. A phase bin of ~0.1 corresponds to ~6,600 s and ~820 s for eRO-QPE1 and eRO-QPE2, respectively. Moreover, XMM-Newton and NICER light curve profiles were fitted with UltraNest44. Motivated by the strong asymmetry in eRO-QPE1 (Figs. 1c, d, 3a), we adopted a model with Gaussian rise and an exponential decay, a generic model often adopted for transients51. eRO-QPE2, on the other hand, can be fitted with a simple Gaussian profile (Fig. 3b), possibly owing to the much shorter timescales. Here we simply highlight the most evident results of timing analysis; a more in depth study of the variability properties of QPEs is deferred to future work. Here the modelling allows us to determine mean values for the duration and recurrence time of the QPEs, which were used for comparison with models of accretion instabilities (see Methods section ‘On accretion flow instabilities’) and compact object binaries (see Methods section ‘On the presence of an orbiting body’). The mean rise-to-decay duration for eRO-QPE1, as observed from the NICER light curve (Fig. 1d), is ~7.6 h (dispersion of ~1.0 h), and the mean peak-to-peak separation is ~18.5 h (dispersion of ~2.7 h). The related duty cycle (here computed simply as mean duration over mean separation) is ~41%. Conversely, eRO-QPE2 shows much narrower and more frequent eruptions (see Fig. 2c): the mean rise-to-decay duration is ~27 min (dispersion of ~3 min), with a mean peak-to-peak separation of ~2.4 h (dispersion of ~5 min) and a duty-cycle of ~19%.
The host galaxies of the QPEs
Very little was known on both galaxies from published multi-wavelength catalogues, except for WISE infrared monitoring, indicating W1 − W2 emission consistent with zero, which is typical of inactive galactic nuclei, for the last few years. Most of our knowledge is based on optical spectra taken with SALT after the X-ray observation. The optical counterpart of eRO-QPE1 is classified as a passive galaxy from the absence of emission lines (Extended Data Fig. 1b), whereas eRO-QPE2 shows very strong and narrow [O ii], Hβ, [O iii], Hα, [N ii] and [S ii] in emission (Extended Data Fig. 2b). The high [O ii]/[O iii] value and that Hβ is as strong as [O iii] are already strongly indicative that star-forming processes are the dominant ionization mechanism52. We computed the flux ratios log([O iii]/Hβ) = −0.05, log([O ii]/Hβ) = 0.44 and log([N ii]/Hα) = −0.68, as well as the [O ii] equivalent width (EW) log EW[OII] = 2.56 and D4,000 = 1.26, where D4,000 is the ratio of the continuum level after and before the 4,000 Å break53. Using standard line diagnostic plots54 we can confirm that indeed eRO-QPE2 can be classified as star-forming. Spectroscopic classification of future QPEs will be crucial to confirm whether their host galaxies are indeed preferentially inactive, as our pilot study suggests, or not. A first census in a statistically significant sample may bring new insights, as has been the case for other transients such as tidal disruption events (TDEs)55,56,57,58.
A preliminary analysis of the properties of the host galaxies of the QPEs was performed by fitting the optical spectra (Extended Data Figs. 1b, 2b) with Firefly59,60. We first re-normalized the flux of the optical spectra using the most recent g-band and r-band archival magnitudes, because SALT spectra are not calibrated to absolute values42. For eRO-QPE1, gri-band photometry (g = 18.7 ± 0.06 mag, r = 18.0 ± 0.05 mag, i = 17.8 ± 0.05 mag) was taken on 30 July 2020 with the Rapid Response Robotic Telescope at Fan Mountain Observatory, indicating that the source did not change substantially with respect to archival photometry61. The total stellar masses inferred with Firefly from the optical spectra are \({M}_{\ast }\approx {3.8}_{-1.9}^{+0.4}\times {10}^{9}{M}_{\odot }\) and \({1.01}_{-0.50}^{+0.01}\times {10}^{9}{M}_{\odot }\) for eRO-QPE1 and eRO-QPE2, respectively. Systematic errors and degeneracy due to the use of different stellar population models62 would push M⁎ to higher values for eRO-QPE1 (~4.8 × 109M☉) and lower values for eRO-QPE2 (~0.6 × 109M☉), enhancing their relative difference. Firefly also yields an estimate of the age of the stellar population and the star-formation rate (SFR), although for medium and low signal-to-noise ratios these estimates are more prone to biases59. For eRO-QPE2, the mean signal-to-noise ratio (~23) is high enough to yield a fairly reliable \({\rm{SFR}}\approx {0.078}_{-0.066}^{+0.001}{M}_{\odot }\,{{\rm{yr}}}^{-1}\), which is also consistent within uncertainties with the SFR that can be estimated from the [O ii] and Hα luminosities63,64. For eRO-QPE1, the mean signal-to-noise ratio (~8) is lower and no reliable estimate of the SFR was obtained. We therefore inferred an upper limit of ~0.01M☉ yr−1 from the absence of narrow emission lines63,64. We report in Extended Data Fig. 6 the M⁎–SFR plane with the two QPEs reported here, together with normal galaxies, and hosts of known TDEs57 and changing-look AGN (CLAGN)65, all taken below z < 0.1 and within the Sloan Digital Sky Survey MPA-JHU DR7 catalogue66. Evidence is mounting that both TDEs57,67 and CLAGN65 might be over-represented in galaxies in the so-called ‘green valley’, perhaps indicating that they are activated in specific periods of galaxy co-evolution with their central black holes. For QPEs, a statistically meaningful sample still needs to be built before reaching any conclusion.
We have estimated that the host galaxy of eRO-QPE1 is more massive than that of eRO-QPE2. We here refrain from quoting absolute values for black hole masses using their scaling relations with the host galaxy properties, because our stellar masses are lower than those used to calibrate them68. However, it is worth mentioning that the relative ratio of ~4–8 in stellar masses between the galaxies of eRO-QPE1 and eRO-QPE2 would propagate to a black hole mass ratio of the order of approximately 10 (ref. 68). This is in line with the X-ray timing properties in eRO-QPE1 and eRO-QPE2, because their peak-to-peak separation and rise-to-decay duration scale roughly by the same amount. Finally, X-ray emission from eRO-QPE1 and eRO-QPE2 was observed to be positionally consistent with the galaxy nucleus for both objects (Extended Data Figs. 1a, 2a; Methods section ‘The two eROSITA QPEs’). If a future QPE is found in a more nearby galaxy we can aim to constrain more precisely the X-ray position with respect to the galactic nucleus. This will allow us to determine conclusively whether or not these phenomena are nuclear.
On accretion flow instabilities
Accretion disks69 with an accretion rate such that radiation pressure dominates in the inner flow are thought to be subject to thermal–viscous instabilities70. The net result of these instabilities is that the luminosity is predicted to oscillate5,6,7,8 with timescales and amplitude proportional to the black hole mass and bolometric luminosity71,72. The predicted light curves profiles show first a stable and slow rise in luminosity, as both temperature and surface density increase while matter is slowly accumulated. Thereafter a sharp luminosity burst is produced by a runaway increase (decrease) in temperature (surface density) propagating outwards within the unstable region. Finally, the inner flow, devoid of the matter supply, cools down rapidly and cycles back to the initial stable state with low temperature and density. Both heating and cooling fronts propagate following thermal timescales6, where τth ≈ α−1(GMBH/R3)−1/2 (where R is the distance from the black hole). These so-called limit-cycle or ‘heartbeat’ instabilities have been successfully applied to a few accreting sources across all mass scales, for instance to the stellar-mass black holes GRS 1915+10520,21,73, IGR J17091-362422 and 4XMM J111816.0-32491074 and to supermassive black holes in a statistical fashion71,72. The similarity of their timing properties with those of QPEs in GSN 069 is remarkable and naturally led to the proposed connection with limit-cycle instabilities for that object. In particular, the symmetry of the eruptions in GSN 069 was compared to the fast heating and cooling phases of the instability1, both following similar τth under the assumption of invariant α across the two phases75. The lack of a slow rise before the eruptions in QPEs, predicted by the instability models, could be due to our limited coverage of the full disk temperature profile in the soft X-ray band.
With the observation of the two QPEs we report here we can now argue against at least this type of accretion disk instability as the origin of QPEs. Specifically, the strong asymmetric nature of the eruptions in eRO-QPE1, which show a faster rise and a much slower decay (Fig. 3a), argues against this interpretation. Qualitatively, our data would suggest that QPEs are not related to τth, because α is not expected to change between the hot and cold phases in AGN75. Moreover, if instead it is the front propagation timescales, following τfront ≈ (H/R)−1τth (where H is the vertical scale height of the disk), or viscous timescales, following τvisc ≈ (H/R)−2τth, that regulates the rise (decay) in the cold (hot) phase, it would imply a thicker flow in the cold and stable phase than in the hot and unstable phase. This runs contrary to the theoretical expectation that unstable flows should be thicker6. The limit-cycle oscillation theory further predicts that once the period, duty cycle and luminosity amplitude are known and a viscosity prescription for the accretion flow is adopted, there are only specific values of MBH and α that unstable sources are allowed to follow8. Here we adopt for eRO-QPE1 (eRO-QPE2) a peak-to-peak period Tpp = 18.5 h (2.4 h), an amplitude A ≈ 294 (11) and a duty cycle D = 41% (19%). The amplitude A is the ratio of the disk luminosity (computed within the 0.001–100-keV range) for peak and quiescence, taken as proxy of the maximum and minimum bolometric luminosity, and D is here defined as the ratio of the flare duration (rise-to-decay Trd) and the period Tpp. We begin by adopting a standard viscosity prescription, with the average stress between the annuli proportional to the gas plus radiation pressure69 Ptot. The allowed MBH and α values for eRO-QPE1 (eRO-QPE2) are MBH ≈ 4 × 106M☉ and α ≈ 5 (MBH ≈ 3 × 106M☉ and α ≈ 3), therefore an unphysically high viscosity parameter would be required. Considering alternative viscosity prescriptions5,8, for eRO-QPE1 (eRO-QPE2) a more reasonable α ≈ 0.1 or 0.01 would correspond to allowed MBH ≈ 2.4 × 103M☉ or MBH ≈ 60M☉ (MBH ≈ 4.3 × 103M☉ or MBH ≈ 30M☉), respectively. The above combinations are either unphysical or very unlikely. Adopting α ≈ 0.2 and alternative viscosity prescriptions, eRO-QPE1 (eRO-QPE2) would yield an intermediate-mass black hole (IMBH) at MBH ≈ 0.9 × 104M☉ (MBH ≈ 1.6 × 104M☉) accreting at ~0.1 (~0.3) of the Eddington limit in quiescence and at ~30 (~3) times the Eddington limit at the peak. However, this IMBH scenario would not account for the opposite asymmetry shown by eRO-QPE1 compared to the theoretical predictions, nor would the resulting thermal timescales be self-consistent for either of the two: for eRO-QPE1 (eRO-QPE2) τth ≈ 20 s (35 s) at 20rg adopting MBH ≈ 0.9 × 104M☉ (MBH ≈ 1.6 × 104M☉), which is orders of magnitude smaller than the observed QPE durations, and the rise-to-peak times would be only reconciled with τth at ~780rg (~250rg). Analogous results can be obtained using the observed properties of RX J1301.9+27472, adopting Tpp ≈ 20 ks (or the second period Tpp ≈ 13 ks), D = 6% (9%) and A ≈ 9.4, the latter obtained taking the ratio of the quoted quiescence and peak 0.3–2.0-keV flux as proxy for a bolometric luminosity ratio: adopting2 α ≈ 0.15 the allowed black hole mass is ~2.2 × 104M☉ (~1.5 × 104M☉), much lower than the quoted2,76 ~(0.8–2.8) × 106M☉.
When a given source is in a ‘sweet-spot’ regime in mass accretion rate, some more recent modified viscosity prescriptions of accretion disks predict the presence of a narrow unstable zone placed within an inner inefficient advection-dominated flow and an outer standard geometrically thin and stable flow9. This model would reduce the propagation timescales by a factor of approximately dR/R, where dR is the radial extent of the unstable zone at a distance R from the black hole, which may help reconcile the model with the dramatic and fast variability observed in CLAGN77. This would not, however, change the inconsistency with the asymmetric shape of the QPEs we report here, nor was it successful in modelling all the observables in GSN 0699. In summary, our data for both of the QPEs reported here are inconsistent with published models for radiation pressure instability5,6,7,8,9. The role of more complex or exotic phenomenology9 should be further explored.
We also note that a fast-rise exponential decay profile—such as the one in eRO-QPE1—can be naturally produced by ionization instability models, which are used for some bursting stellar-mass accreting compact objects78. To our knowledge there is no evidence so far of such instabilities taking place in AGN79. In addition, the predicted timescales are many orders of magnitude longer than QPEs for both AGN79,80,81 and IMBH masses82.
Finally, we discuss disk warping and tearing induced by Lense–Thirring precession83,84, which has been recently qualitatively compared also to QPE sources85. In this work we presented evidence of QPEs being observed in previously inactive galaxies, therefore the accretion flow in these systems should be young. Moreover, a key element of disk warping and tearing due to Lense–Thirring precession is that mass needs to flow in from large inclination with respect to the black hole spin. Both conditions are satisfied if the accretion flow is formed, for instance, by a fully stripped TDE. However, in this case the warped inner flow would be damped very fast86, which would be in contrast with QPEs lasting at least months1 (Figs. 1, 2) or even years2. A more quantitative comparison is beyond the reach of this work and of current disk warping and tearing simulations, but this is a promising scenario worth exploring in the future.
On the presence of an orbiting body
Periodic variability is also often associated with binary systems of compact objects23 and the connection with the quasi-periodic nuclear emission observed in QPEs of interest for future work. We here assume the main body to be a supermassive black hole ranging between approximately 104M☉ and 107M☉ and we first consider the presence of a second orbiting supermassive black hole with a similar mass. There are several reasons which, when combined, disfavour such a scenario. First, simulations show that the accretion flow of such objects is composed by a circum-binary disk with two inner small mini-disks87,88,89, which are thought to produce a quasi-sinusoidal modulated emission90,91. This signature can be detected in transient surveys92,93 or in single sources94, with a well known extreme case being OJ 28795,96. However, so far there is no evidence of such variability in optical and UV data1 of QPEs (Fig. 1c, 2c), in particular in eRO-QPE1, which was covered in the g and r bands by the Zwicky Transient Facility DR397 until the end of 2019. Nor can this prediction be reconciled with the dramatic non-sinusoidal eruptions observed in X-rays, even in the case of binary self-lensing98 which can produce sharper bursts, albeit achromatic, and therefore in contrast with the energy dependence of QPEs1,2. Moreover, we do not observe peculiar single- or double-peaked emission lines99,100,101 and this cannot be reconciled by enhanced obscuration102, because infrared photometry in QPEs is not AGN-like (WISE has observed stable W1 − W2 ≈ 0 emission for the past 6–7 yr) and X-rays do not indicate the presence of strong absorption. Second, supermassive black hole binaries are expected to form mostly via galactic mergers103,104, but the host galaxies of the two QPEs we report here look unperturbed (Extended Data Figs. 1a, 2a). Perhaps most importantly, a binary of supermassive black holes observed with a periodicity of the order of hours, such as the four observed QPEs, would show a large period derivative due to gravitational wave emission, and would be relatively close to merger. To have (at least) four such objects very close to merger within z ≈ 0.02–0.05 is very unlikely105 and would imply that they are much more common in the local Universe than observations suggest92,93.
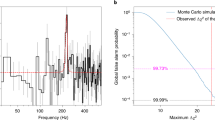
Under the simplified assumption that the orbital evolution is dominated by gravitational waves emission, Extended Data Fig. 7 shows the allowed parameter space in terms of the derivative of the period, \(\dot{P}\), and M2 for a range of MBH,1 ≈ 104M☉–107M☉ and zero- or high-eccentricity orbit (eO ≈ 0.9), given the rest-frame period of both eRO-QPE1 and eRO-QPE2. We have additionally imposed M2 ≤ MBH,1. For both sources we can draw a tentative line at the minimum period derivative that, if present, we would have measured already within the available observations: somewhat conservatively, we adopt a period decrease of one cycle over the 15 observed by NICER for eRO-QPE1 and the nine observed by XMM-Newton for eRO-QPE2 (Figs. 1d, 2c). Our constraint on \(\dot{P}\) is not very stringent for eRO-QPE1 and only high M2 and eccentricities are disfavoured; instead, for eRO-QPE2 only an orbiting IMBH, or smaller, is allowed for zero eccentricity, whereas only a stellar-mass compact object is allowed for high eccentricity (eO ≈ 0.9). Future observations of eRO-QPE1 and eRO-QPE2 in the next months may lead to tighter constraints on the mass and eccentricity of the putative orbiting body.
The preliminary conclusion of our analysis is that, if QPEs are driven by the presence of an orbiting body around a central black hole, it is more likely that this is a compact object with a mass considerably smaller than the ~104M☉–107M☉ assumed for the main body. This scenario could make QPEs a viable candidate for the electromagnetic counterparts of the so-called extreme-mass-ratio inspirals (EMRIs)11,12,13, with considerable implications for multi-messenger astrophysics and cosmology14,15. Interestingly, it has been recently suggested for GSN 069 that a stellar-mass compact object orbiting around a supermassive black hole could be the origin of QPEs: a white dwarf of ~0.2M☉ on a highly eccentric orbit (eO ≈ 0.94) could reproduce the mass inflow rate needed to produce the observed X-ray luminosity averaged over a QPE cycle10. This is reminiscent of a suggested, albeit still observationally elusive, EMRI-formation channel13,24,25,26. For GSN 069, a possible explanation of the QPE-free X-ray bright and decaying phase could be given by an accretion flow expanding and intercepting the body at a later time1; or if the orbiting body was originally a massive star and the stripped envelope produced the TDE-like behaviour of the past decade1 while the remaining core started interacting with the newly born or expanded accretion flow only at a later stage, which would also explain the relatively small mass required by the white dwarf calculations10. For the other QPEs that did not show evidence of a past X-ray bright and decaying phase, this scenario is not necessary and the interaction with a second stellar-mass (or more massive) compact object could qualitatively reproduce the periodic behaviour (Extended Data Fig. 7b). Future X-ray observations of the known QPEs would help in further constraining the possible orbital evolution. It should be pointed out that these calculations so far only match the average observed QPE luminosity with the mass inflow rate required to produce it10, but details on the exact physical mechanism that would produce these X-ray bursts are still unknown (see Methods section ‘On accretion flow instabilities’).
Finally, we address the lack of UV and optical variability in the scenario of an orbiting body. The X-ray plateau at minimum shows an almost featureless accretion disk thermal spectrum1,2 (Extended Data Fig. 5), which could have been built up during the first orbiting cycles. This accretion flow should be unusually small due to the lack of a broad line region3,4 (Extended Data Figs. 1b, 2b), which would respond in light-days and that, if present, should have been observed in the SALT spectra taken months after the X-ray QPEs. The lack of strong UV and optical variability might be then due to the fact that the accretion disk is not large enough to even emit strong enough UV–optical radiation to emerge above the galaxy emission, which we can assume to be most of the observed L ≈ 4.0 × 1041 erg s−1 (L ≈ 4.3 × 1041 erg s−1) in the OM-UVW1 filter at 2,910 Å for eRO-QPE1 (eRO-QPE2). Using a simplified but physically motivated accretion disk model106 for a spin-zero black hole accreting at ~0.1 of the Eddington limit, we computed the distance at which the bulk of 2,910-Å radiation would be emitted, namely ~1,100rg and ~500rg for masses of 105M☉ and 106M☉, respectively. This would shift to even larger radii for increasing accretion rate (for example, ~1,850rg and ~860rg at ~0.5 of the Eddington limit), whereas even for high spinning sources (dimensionless spin parameter ~0.9) the peak of OM-UVW1 flux would still come from ~775rg and ~360rg. Furthermore, the predicted OM-UVW1 disk luminosity would be at least one or two orders of magnitude lower than the observed L ≈ 4.0 × 1041 erg s−1 in the most luminous scenario. Therefore, even a UV–optical eruption 100 times brighter than the plateau would be barely detectable above the galaxy component.
Predicted numbers
Detailed self-consistency calculations on the predicted rate of such EMRI events, as compared to QPE rates, are required but are beyond the scope of this paper. Instead, we can provide here a rough model-independent estimate of the expected number of observed QPEs, regardless of their origin. Convolving the black hole mass function107 between approximately 104.5M☉ and 106.5M☉ up to z ≈ 0.03 with the eROSITA sensitivity yields approximately 100 sources, a number that is then reduced with some educated guesses on some unknowns: during what fraction of their X-ray bright phase such sources undergo QPE behaviour (the biggest unknown; for example, >20% for GSN 069); how many such sources are obscured and missed (~2/3); how many times we detect ongoing QPEs given the eROSITA sampling (depends on the period and the burst duration; for example, ~20% for GSN 069). This results in a (extremely uncertain) number of the order of unity per eRASS scan in the eROSITA-DE hemisphere; however, this is in agreement with our pilot study of the first few months of eROSITA operations. Thus, the low observed numbers do not necessarily imply that these events are a rare phenomenon intrinsically and they can in fact be a fairly common product of the co-evolution of black holes with their host galaxies28. With a statistically meaningful sample of QPEs, inverting this calculation may allow us to constrain the black hole mass function in a poorly known mass regime27.
Data availability
With the exception of eROSITA proprietary data, the data used in this work are public and available from the corresponding data archives (XMM-Newton, http://nxsa.esac.esa.int/nxsa-web/#search; NICER, https://heasarc.gsfc.nasa.gov/docs/nicer/nicer_archive.html) or they will be soon, after the remaining proprietary period expires. Most of data may be available from the corresponding author on reasonable request.
References
Miniutti, G. et al. Nine-hour X-ray quasi-periodic eruptions from a low-mass black hole galactic nucleus. Nature 573, 381–384 (2019).
Giustini, M., Miniutti, G. & Saxton, R. X-ray quasi-periodic eruptions from the galactic nucleus of RX J1301.9+2747. Astron. Astrophys. 636, L2 (2020).
Miniutti, G. et al. A high Eddington-ratio, true Seyfert 2 galaxy candidate: implications for broad-line region models. Mon. Not. R. Astron. Soc. 433, 1764–1777 (2013).
Sun, L., Shu, X. W. & Wang, T. R. X. J1301.9+2747: a highly variable Seyfert galaxy with extremely soft X-ray emission. Astrophys. J. 768, 167 (2013).
Merloni, A. & Nayakshin, S. On the limit-cycle instability in magnetized accretion discs. Mon. Not. R. Astron. Soc. 372, 728–734 (2006).
Janiuk, A., Czerny, B. & Siemiginowska, A. Radiation pressure instability driven variability in the accreting black holes. Astrophys. J. 576, 908–922 (2002).
Janiuk, A. & Czerny, B. On different types of instabilities in black hole accretion discs: implications for X-ray binaries and active galactic nuclei. Mon. Not. R. Astron. Soc. 414, 2186–2194 (2011).
Grzędzielski, M., Janiuk, A., Czerny, B. & Wu, Q. Modified viscosity in accretion disks: application to Galactic black hole binaries, intermediate mass black holes, and active galactic nuclei. Astron. Astrophys. 603, A110 (2017).
Sniegowska, M., Czerny, B., Bon, E. & Bon, N. Possible mechanism for multiple changing-look phenomena in active galactic nuclei. Astron. Astrophys. 641, A167 (2020).
King, A. GSN 069 – a tidal disruption near miss. Mon. Not. R. Astron. Soc. 493, L120–L123 (2020).
Amaro-Seoane, P. et al. Intermediate and extreme-mass-ratio inspirals—astrophysics, science applications and detection using LISA. Class. Quantum Gravity 24, R113–R169 (2007).
Babak, S. et al. Science with the space-based interferometer LISA. V. Extreme mass-ratio inspirals. Phys. Rev. D 95, 103012 (2017).
Wang, Y. Y., Wang, F. Y., Zou, Y. C. & Dai, Z. G. A bright electromagnetic counterpart to extreme mass ratio inspirals. Astrophys. J. Lett. 886, 22 (2019).
Bloom, J. S. et al. Astro2010 decadal survey whitepaper: coordinated science in the gravitational and electromagnetic skies. Preprint at https://arxiv.org/abs/0902.1527 (2009).
Tamanini, N. Late time cosmology with LISA: probing the cosmic expansion with massive black hole binary mergers as standard sirens. J. Phys. Conf. Ser. 840, 012029 (2017).
Predehl, P. et al. The eROSITA X-ray telescope on SRG. Astron. Astrophys. 647, A1 (2021).
McHardy, I. M., Koerding, E., Knigge, C., Uttley, P. & Fender, R. P. Active galactic nuclei as scaled-up Galactic black holes. Nature 444, 730–732 (2006).
Netzer, H. Revisiting the unified model of active galactic nuclei. Annu. Rev. Astron. Astrophys. 53, 365–408 (2015).
Chen, J. et al. The spatial extension of extended narrow line regions in MaNGA AGN. Mon. Not. R. Astron. Soc. 489, 855–867 (2019).
Taam, R. E., Chen, X. & Swank, J. H. Rapid bursts from GRS 1915+105 with RXTE. Astrophys. J. 485, L83–L86 (1997).
Belloni, T., Klein-Wolt, M., Méndez, M., van der Klis, M. & van Paradijs, J. A model-independent analysis of the variability of GRS 1915+105. Astron. Astrophys. 355, 271–290 (2000).
Altamirano, D. et al. The faint ‘heartbeats’ of IGR J17091–3624: an exceptional black hole candidate. Astrophys. J. Lett. 742, 17 (2011).
De Rosa, A. et al. The quest for dual and binary supermassive black holes: a multi-messenger view. New Astron. Rev. 86, 101525 (2019).
Sesana, A., Vecchio, A., Eracleous, M. & Sigurdsson, S. Observing white dwarfs orbiting massive black holes in the gravitational wave and electro-magnetic window. Mon. Not. R. Astron. Soc. 391, 718–726 (2008).
Zalamea, I., Menou, K. & Beloborodov, A. M. White dwarfs stripped by massive black holes: sources of coincident gravitational and electromagnetic radiation. Mon. Not. R. Astron. Soc. Lett. 409, L25–L29 (2010).
Eracleous, M. et al. An arena for multi-messenger astrophysics: inspiral and tidal disruption of white dwarfs by massive black holes. Bull. Am. Astron. Soc. 51, 10 (2019).
Kelly, B. V. & Merloni, A. Mass functions of supermassive black holes across cosmic time. Adv. Astron. 2012, 970858 (2012).
Heckman, T. M. & Best, P. N. The coevolution of galaxies and supermassive black holes: insights from surveys of the contemporary Universe. Annu. Rev. Astron. Astrophys. 52, 589–660 (2014).
Amaro-Seoane, P. et al. Laser Interferometer Space Antenna. Preprint at https://arxiv.org/abs/1702.00786 (2017).
Salvato, M. et al. Finding counterparts for all-sky X-ray surveys with NWAY: a Bayesian algorithm for cross-matching multiple catalogues. Mon. Not. R. Astron. Soc. 473, 4937–4955 (2018).
Dey, A. et al. Overview of the DESI Legacy Imaging Surveys. Astron. J. 157, 168 (2019).
Buckley, D. A. H., Swart, G. P. & Meiring, J. G. Completion and commissioning of the Southern African Large Telescope. In Proc. SPIE 6267: Ground-based and Airborne Telescopes (ed. Stepp L. M.) 62670Z (SPIE, 2006).
Trümper, J. The ROSAT mission. Adv. Space Res. 2, 241–249 (1982).
Saxton, R. D. et al. The first XMM-Newton slew survey catalogue: XMMSL1. Astron. Astrophys. 480, 611–622 (2008).
Turner, M. J. L. et al. The European Photon Imaging Camera on XMM-Newton: the MOS cameras. Astron. Astrophys. 365, L27–L35 (2001).
Strüder, L. et al. The European Photon Imaging Camera on XMM-Newton: the pn-CCD camera. Astron. Astrophys. 365, L18–L26 (2001).
Mason, K. O. et al. The XMM-Newton optical/UV monitor telescope. Astron. Astrophys. 365, L36–L44 (2001).
Gendreau, K. C., Arzoumanian, Z. & Okajima, T. The Neutron star Interior Composition ExploreR (NICER): an Explorer mission of opportunity for soft X-ray timing spectroscopy. In Proc. SPIE 8443: Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray (eds Takahashi, T. et al.) 844313 (SPIE, 2012).
Arzoumanian, Z. et al. The neutron star interior composition explorer (NICER): mission definition. In Proc. SPIE 9144: Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray (eds Takahashi, T. et al.) 914420 (SPIE, 2014).
Burgh, E. B. et al. Prime Focus Imaging Spectrograph for the Southern African Large Telescope: optical design. In Proc. SPIE 4841: Instrument Design and Performance for Optical/Infrared Ground-based Telescopes (eds Iye, M. & Moorwood, A. F. M.) 1463–1471 (SPIE, 2003).
Crawford, S. M. et al. PySALT: the SALT science pipeline. In Proc. SPIE 7737: Observatory Operations: Strategies, Processes, and Systems III (eds Silva, D. R. et al.) 773725 (SPIE, 2010).
Buckley, D. A. H. et al. A comparison between SALT/SAAO observations and kilonova models for AT 2017gfo: the first electromagnetic counterpart of a gravitational wave transient – GW170817. Mon. Not. R. Astron. Soc. Lett. 474, L71–L75 (2018).
Buchner, J. et al. X-ray spectral modelling of the AGN obscuring region in the CDFS: Bayesian model selection and catalogue. Astron. Astrophys. 564, A125 (2014).
Buchner, J. Collaborative nested sampling: Big Data versus complex physical models. Publ. Astron. Soc. Pacif. 131, 108005 (2019).
Arnaud, K. A. XSPEC: the first ten years. In Astronomical Data Analysis Software and Systems V (eds Jacoby, G. H. & Barnes, J.) http://iraf.noao.edu/ADASS/adass_proc/adass_95/arnaudk/arnaudk.html (1996).
Simmonds, C., Buchner, J., Salvato, M., Hsu, L.-T. & Bauer, F. E. X. Z. Deriving redshifts from X-ray spectra of obscured AGN. Astron. Astrophys. 618, A66 (2018).
Cash, W. Parameter estimation in astronomy through application of the likelihood ratio. Astrophys. J. 228, 939–947 (1979).
Wilms, J., Allen, A. & McCray, R. On the absorption of X-rays in the interstellar medium. Astrophys. J. 542, 914–924 (2000).
Mitsuda, K. et al. Energy spectra of low-mass binary X-ray sources observed from TENMA. Publ. Astron. Soc. Jpn. 36, 741–759 (1984).
HI4PI Collaboration. HI4PI: a full-sky H I survey based on EBHIS and GASS. Astron. Astrophys. 594, A116 (2016).
Van Velzen, S. The first tidal disruption flare in ZTF: from photometric selection to multi-wavelength characterization. Astrophys. J. 872, 198 (2019).
Silverman, J. D. et al. Ongoing and co-evolving star formation in zCOSMOS galaxies hosting active galactic nuclei. Astrophys. J. 696, 396–410 (2009).
Zabludoff, A. I. et al. The environment of ‘E+A’ galaxies. Astrophys. J. 466, 104–113 (1996).
Comparat, J. Investigating emission-line galaxy surveys with the Sloan Digital Sky Survey infrastructure. Mon. Not. R. Astron. Soc. 428, 1498–1517 (2013).
Arcavi, I. et al. A continuum of H- to He-rich tidal disruption candidates with a preference for E+A galaxies. Astrophys. J. 793, 38 (2014).
French, K. D., Arcavi, I. & Zabludoff, A. Tidal disruption events prefer unusual host galaxies. Astrophys. J. Lett. 818, 21 (2016).
Law-Smith, J., Ramirez-Ruiz, E., Ellison, S. L. & Foley, R. J. Tidal disruption event host galaxies in the context of the local galaxy population. Astrophys. J. 850, 22 (2017).
Van Velzen, S. et al. Seventeen tidal disruption events from the first half of ZTF survey observations: entering a new era of population studies. Astrophys. J. 908, 4 (2021).
Wilkinson, D. M., Maraston, C., Goddard, D., Thomas, D. & Parikh, T. FIREFLY (Fitting IteRativEly For Likelihood analYsis): a full spectral fitting code. Mon. Not. R. Astron. Soc. 472, 4297–4326 (2017).
Maraston, C. et al. Stellar population models based on the SDSS-IV MaStar library of stellar spectra—I. Intermediate-age/old models. Mon. Not. R. Astron. Soc. 496, 2962–2997 (2020).
Abbott, T. M. C. et al. The Dark Energy Survey: data release 1. Astrophys. J. Suppl. Ser. 239, 18 (2018).
Maraston, C. & Stroemback, G. Stellar population models at high spectral resolution. Mon. Not. R. Astron. Soc. 418, 2785–2811 (2011).
Kennicutt, R. C., Jr. Star formation in galaxies along the Hubble sequence. Annu. Rev. Astron. Astrophys. 36, 189–231 (1998).
Kewley, L. J., Geller, M. J. & Jansen, R. A. [O ii] as a star formation rate indicator. Astron. J. 127, 2002–2030 (2004).
Dodd, S. A., Law-Smith, J. A. P., Auchettl, K., Ramirez-Ruiz, E. & Foley, R. J. The landscape of galaxies harboring changing-look active galactic nuclei in the local Universe. Astrophys. J. Lett. 907, 21 (2021).
Brinchmann, J. et al. The physical properties of star-forming galaxies in the low-redshift Universe. Mon. Not. R. Astron. Soc. 351, 1151–1179 (2004).
Hammerstein, E. et al. Tidal disruption event hosts are green and centrally concentrated: signatures of a post-merger system. Astrophys. J. Lett. 908, 20 (2021).
Reines, A. E. & Volonteri, M. Relations between central black hole mass and total galaxy stellar mass in the local Universe. Astrophys. J. 813, 82 (2015); correction 879, 133 (2019).
Shakura, N. I. & Sunyaev, R. A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 24, 337–355 (1973).
Lightman, A. P. & Eardley, D. M. Black holes in binary systems: instability of disk accretion. Astrophys. J. 187, L1–L3 (1974).
Czerny, B., Siemiginowska, A., Janiuk, A., Nikiel-Wroczyński, B. & Stawarz, Ł. Accretion disk model of short-timescale intermittent activity in young radio sources. Astrophys. J. 698, 840–851 (2009).
Wu, Q. et al. The Universal ‘heartbeat’ oscillations in black hole systems across the mass-scale. Astrophys. J. 833, 79 (2016).
Neilsen, J., Remillard, R. A. & Lee, J. C. The physics of the ‘heartbeat’ state of GRS 1915+105. Astrophys. J. 737, 69 (2011).
Motta, S. et al. The slow heartbeats of an ultraluminous X-ray source in NGC 3621. Astrophys. J. 898, 174 (2020).
Janiuk, A., Czerny, B., Siemiginowska, A. & Szczerba, R. On the turbulent α-disks and the intermittent activity in active galactic nuclei. Astrophys. J. 602, 595–602 (2004).
Shu, X. W. et al. Central engine and host galaxy of RXJ 1301.9+2747: a multiwavelength view of a low-mass black hole active galactic nuclei with ultra-soft X-ray emission. Astrophys. J. 837, 3 (2017).
MacLeod, C. L. et al. A systematic search for changing-look quasars in SDSS. Mon. Not. R. Astron. Soc. 457, 389–404 (2016).
Hameury, J. M. A review of the disc instability model for dwarf novae, soft X-ray transients and related objects. Adv. Space Res. 66, 1004–1024 (2020).
Hameury, J. M., Viallet, M. & Lasota, J.-P. The thermal–viscous disk instability model in the AGN context. Astron. Astrophys. 496, 413–421 (2009).
Lin, D. N. C. & Shields, G. A. Accretion disks and periodic outbursts of active galactic nuclei. Astrophys. J. 305, 28 (1986).
Yan, Z. & Xie, F.-G. A decades-long fast-rise-exponential-decay flare in low-luminosity AGN NGC 7213. Mon. Not. R. Astron. Soc. 475, 1190–1197 (2018).
Lasota, J.-P. et al. The origin of variability of the intermediate-mass black-hole ULX system HLX-1 in ESO 243-49. Astrophys. J. 735, 89 (2011).
Nixon, C., King, A., Price, D. & Frank, J. Tearing up the disk: how black holes accrete. Astrophys. J. Lett. 757, 24 (2012).
Raj, A., Nixon, C. & Dogan, S. Disk tearing: numerical investigation of warped disk instability. Astrophys. J. 909, 81 (2021).
Raj, A. & Nixon, C. Disk tearing: implications for black hole accretion and AGN variability. Astrophys. J. 909, 82 (2021).
Franchini, A., Lodato, G. & Facchini, S. Lense–Thirring precession around supermassive black holes during tidal disruption events. Mon. Not. R. Astron. Soc. 455, 1946–1956 (2016).
Farris, B. D., Duffell, P., MacFadyen, A. I. & Haiman, Z. Binary black hole accretion from a circumbinary disk: gas dynamics inside the central cavity. Astrophys. J. 783, 134 (2014).
Bowen, D. B. et al. Quasi-periodic behavior of mini-disks in binary black holes approaching merger. Astrophys. J. Lett. 853, 17 (2018).
Tang, Y., Haiman, Z. & MacFadyen, A. The late inspiral of supermassive black hole binaries with circumbinary gas discs in the LISA band. Mon. Not. R. Astron. Soc. 476, 2249–2257 (2018).
Farris, B. D., Duffell, P., MacFadyen, A. I. & Haiman, Z. Characteristic signatures in the thermal emission from accreting binary black holes. Mon. Not. R. Astron. Soc. 446, L36–L40 (2015).
D’Orazio, D. J., Haiman, Z. & Schiminovich, D. Relativistic boost as the cause of periodicity in a massive black-hole binary candidate. Nature 525, 351–353 (2015).
Graham, M. J. A systematic search for close supermassive black hole binaries in the Catalina Real-time Transient Survey. Mon. Not. R. Astron. Soc. 453, 1562–1576 (2015).
Charisi, M. et al. A population of short-period variable quasars from PTF as supermassive black hole binary candidates. Mon. Not. R. Astron. Soc. 463, 2145–2171 (2016).
Graham, M. J. et al. A possible close supermassive black-hole binary in a quasar with optical periodicity. Nature 518, 74–76 (2015).
Sillanpää, A., Haarala, S., Valtonen, M. J., Sundelius, B. & Byrd, G. G. OJ 287: binary pair of supermassive black holes. Astrophys. J. 325, 628–634 (1988).
Valtonen, M. et al. A massive binary black-hole system in OJ 287 and a test of general relativity. Nature 452, 851–853 (2008).
Graham, M. J. et al. The Zwicky Transient Facility: science objectives. Publ. Astron. Soc. Pacif. 131, 078001 (2019).
D’Orazio, D. J. & Di Stefano, R. Periodic self-lensing from accreting massive black hole binaries. Mon. Not. R. Astron. Soc. 474, 2975–2986 (2018).
Wang, J.-M. et al. Active galactic nuclei with double-peaked narrow lines: are they dual active galactic nuclei? Astrophys. J. 705, L76–L80 (2009).
Smith, K. L. et al. A search for binary active galactic nuclei: double-peaked [O iii] AGNs in the Sloan Digital Sky Survey. Astrophys. J. 716, 866–877 (2010).
Eracleous, M., Boroson, T. A., Halpern, J. P. & Liu, J. A large systematic search for close supermassive binary and rapidly recoiling black holes. Astrophys. J. Suppl. Ser. 201, 23 (2012).
Pfeifle, R. W. et al. Buried black hole growth in IR-selected mergers: new results from Chandra. Astrophys. J. 875, 117 (2019).
Khan, F. M., Fiacconi, D., Mayer, L., Berczik, P. & Just, A. Swift coalescence of supermassive black holes in cosmological mergers of massive galaxies. Astrophys. J. 828, 73 (2016).
Kelley, L. Z., Blecha, L. & Hernquist, L. Massive black hole binary mergers in dynamical galactic environments. Mon. Not. R. Astron. Soc. 464, 3131–3157 (2017).
Payne, A. et al. ASASSN-14ko is a periodic nuclear transient in ESO 253-G003. Preprint at https://arxiv.org/abs/2009.03321 (2020).
Arcodia, R., Merloni, A., Nandra, K. & Ponti, G. Testing the disk–corona interplay in radiatively-efficient broad-line AGN. Astron. Astrophys. 628, A135 (2019).
Merloni, A. & Heintz, S. A synthesis model for AGN evolution: supermassive black holes growth and feedback modes. Mon. Not. R. Astron. Soc. 388, 1011–1030 (2008).
Acknowledgements
We are grateful to the XMM-Newton Project Scientist N. Schartel for the DDT observation of eRO-QPE2; we also thank the XMM-Newton Science Operations team for performing it along with the two approved ToOs on eRO-QPE1 with a relatively short notice before the end of the visibility window. R.A. thanks M. Gilfanov, K. Dennerl and S. Carpano for discussions. G.P. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 865637). This work is based on data from eROSITA, the primary instrument aboard SRG, a joint Russian–German science mission supported by the Russian Space Agency (Roskosmos), in the interests of the Russian Academy of Sciences represented by its Space Research Institute (IKI), and the Deutsches Zentrum für Luft- und Raumfahrt (DLR). The SRG spacecraft was built by Lavochkin Association (NPOL) and its subcontractors, and is operated by NPOL with support from the Max Planck Institute for Extraterrestrial Physics (MPE). The development and construction of the eROSITA X-ray instrument was led by MPE, with contributions from the Dr. Karl Remeis Observatory Bamberg & ECAP (FAU Erlangen-Nuernberg), the University of Hamburg Observatory, the Leibniz Institute for Astrophysics Potsdam, and the Institute for Astronomy and Astrophysics of the University of Tübingen, with the support of DLR and the Max Planck Society. The Argelander Institute for Astronomy of the University of Bonn and the Ludwig Maximilians Universität München also participated in the science preparation for eROSITA. The eROSITA data shown here were processed using the eSASS/NRTA software system developed by the German eROSITA consortium. Some of the observations were obtained using the Southern African Large Telescope (SALT) as part of the Large Science Programme on transient (2018-2-LSP-001; PI: D.A.H.B.). Polish participation in SALT is funded by grant no. MNiSW DIR/WK/2016/07. D.A.H.B. is supported by the National Research Foundation (NRF) of South Africa. M.G. is supported by the Polish NCN MAESTRO grant 2014/14/A/ST9/00121. M.K. is supported by DFG grant KR 3338/4-1. This work is partly supported by the Optical and Near-infrared Astronomy Inter-University Cooperation Program and the Grants-in-Aid of the Ministry of Education of Japan.
Funding
Open access funding provided by Max Planck Society.
Author information
Authors and Affiliations
Contributions
R.A. wrote the article, developed the method to search for QPE candidates, was PI of XMM-Newton and NICER follow-up observations, and performed most of the data analysis. A. Merloni is PS/PI of eROSITA and followed and improved the project, the strategy of XMM-Newton and NICER follow-up observing campaigns and the writing of the article. K.N. followed and improved the project, the strategy of XMM-Newton and NICER follow-up proposals and the writing of the article. J.B. developed part of the code used for spectral and timing analysis and helped R.A. with XMM-Newton data analysis and with the development of the method to search for QPE candidates. M. Salvato led the counterpart association and significantly contributed to the interpretation and analysis of the photometry and optical spectroscopy. D.P. and R.R. performed most of the NICER data analysis. J.C. performed some of the analysis of optical spectroscopy and improved its interpretation. G.L. performed the astrometry of eROSITA and XMM-Newton data. G.P. significantly improved the writing of the article and encouraged the pursuit of this project. A. Malyali and J.W. directly contributed to the analysis of XMM-Newton light curves, optical images and counterpart association. Z.A., K.G. and C.M. scheduled, monitored and processed NICER observations. D.A.H.B. instigated the SALT observations and M.G. processed related data. E.K. and M.K. improved the scientific interpretation and presentation of the manuscript. M.E.R.-C. contributed to development of the method to search for QPE candidates. A.R. contributed to XMM-Newton observing proposals and with A.S. led the triggering of SALT observations from the eROSITA-DE Consortium. M. Schramm performed and processed photometry data from the Rapid Response Robotic Telescope. All authors contributed to improve the projects from different sides throughout the process.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 eRO-QPE1 position and identification.
a, Legacy DR8 image cut-out around the optical counterpart of eRO-QPE1. Red and green circles represent the astrometry-corrected eROSITA and XMM-Newton EPIC-pn positions, respectively, with 1σ positional uncertainties. The EPIC-pn position was corrected excluding the target (blue cross) to ensure an unbiased estimate of the possible positional offset. Image reproduced from Legacy Surveys / D. Lang (Perimeter Institute) under a CC-BY-4.0 licence. b, SALT spectra of eRO-QPE1 shown in black and blue with related 1σ errors as shaded regions. The cyan spectrum represents a re-normalized sky spectrum to guide the eye for the residual sky feature around 5,577 Å.
Extended Data Fig. 2 eRO-QPE2 position and identification.
As in Extended Data Fig. 1, for eRO-QPE2. Green pixels in a are artefacts or missing data in the optical image. Image in a reproduced from Legacy Surveys / D. Lang (Perimeter Institute) under a CC-BY-4.0 licence.
Extended Data Fig. 3 eRO-QPE1 spectral fit results.
XMM-Newton EPIC-pn light-curve (top panel) and time-resolved spectroscopy fit results for spectra extracted in the 500-s time bins (bottom panels) of the two XMM-Newton observations of eRO-QPE1 (left, XMM1; right, XMM2) using an accretion disk model (diskbb): in particular, the evolution of the peak accretion disk temperature (Tin, k = kB) and the normalization (norm), which is proportional to the inner radius once distance and inclination are known. The time evolution of the 0.5–2.0-keV flux (F0.5–2.0keV) and luminosity (L0.5–2.0keV) is also shown in the bottom panel. The quiescence level is fitted by combining the first part of both XMM-Newton observations. It is shown with a dashed line because, due to low counts, the fit is more uncertain (see Extended Data Fig. 5a). Median fit values and fluxes of the high and low eROSITA states are reported with orange and red arrows pointing left (upper limits (UL) are denoted with diagonal arrows). 1σ uncertainties on the fit results are shown with shaded regions around the median.
Extended Data Fig. 4 eRO-QPE2 spectral fit results.
As in Extended Data Fig. 3, for eRO-QPE2. Here the eROSITA upper limit (UL) of the low state is reported at 3σ.
Extended Data Fig. 5 eRO-QPE1 and eRO-QPE2 spectra.
a, XMM-Newton EPIC-pn source plus background (bkg) spectra for eRO-QPE1. Red, orange and green data correspond to quiescence and to the peak of the second and first XMM-Newton observations, respectively, with error bars showing 1σ uncertainties. The related solid lines show the unabsorbed source model obtained with diskbb, just for visualization. The grey line represents the background spectrum alone. The plateau is shown with a dotted line because, due to low counts, the fit is more uncertain. b, As in a, for eRO-QPE2. Here green data represent one of the peaks and the additional dashed lines indicate the absorbed source model.
Extended Data Fig. 6 The properties of the host galaxies of the QPEs.
Stellar mass M⁎ and star-formation rate (SFR) for eRO-QPE1 (blue) and eRO-QPE2 (red), with related 1σ uncertainties; for eRO-QPE1, SFR is largely unconstrained (see Methods section ‘The host galaxies of the QPEs’). For a comparison, normal galaxies66, TDEs57 and CLAGN65, all below z < 0.1, are also shown.
Extended Data Fig. 7 Constraints on a secondary orbiting body.
a, Allowed parameter space in terms of the derivative of the period \(\dot{P}\) and secondary mass M2 for a range of primary mass MBH,1 ≈ 104M☉–107M☉ and zero (solid lines) or high orbital eccentricity (eO ≈ 0.9, dotted lines), in which we can reproduce the rest-frame period of eRO-QPE1. We have additionally imposed M2 ≤ MBH,1. We have drawn an approximate threshold at the minimum value of \(\dot{P}\) which we would have measured within the available observations, corresponding to a period decrease of one QPE cycle over the 15 observed by NICER (Fig. 1d). The excluded region is shaded in red. b, As in a, for eRO-QPE2, and adopting as tentative minimum \(\dot{P}\) a period decrease of one cycle over the nine observed with XMM-Newton (Fig. 2c).
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arcodia, R., Merloni, A., Nandra, K. et al. X-ray quasi-periodic eruptions from two previously quiescent galaxies. Nature 592, 704–707 (2021). https://doi.org/10.1038/s41586-021-03394-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03394-6
This article is cited by
-
X-ray eruptions every 22 days from the nucleus of a nearby galaxy
Nature Astronomy (2024)
-
Science with a Small Two-Band UV-Photometry Mission III: Active Galactic Nuclei and Nuclear Transients
Space Science Reviews (2024)
-
Monthly quasi-periodic eruptions from repeated stellar disruption by a massive black hole
Nature Astronomy (2023)
-
Massive black holes flaring up time and again
Nature Astronomy (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.