Abstract
The trapped-ion quantum charge-coupled device (QCCD) proposal1,2 lays out a blueprint for a universal quantum computer that uses mobile ions as qubits. Analogous to a charge-coupled device (CCD) camera, which stores and processes imaging information as movable electrical charges in coupled pixels, a QCCD computer stores quantum information in the internal state of electrically charged ions that are transported between different processing zones using dynamic electric fields. The promise of the QCCD architecture is to maintain the low error rates demonstrated in small trapped-ion experiments3,4,5 by limiting the quantum interactions to multiple small ion crystals, then physically splitting and rearranging the constituent ions of these crystals into new crystals, where further interactions occur. This approach leverages transport timescales that are fast relative to the coherence times of the qubits, the insensitivity of the qubit states of the ion to the electric fields used for transport, and the low crosstalk afforded by spatially separated crystals. However, engineering a machine capable of executing these operations across multiple interaction zones with low error introduces many difficulties, which have slowed progress in scaling this architecture to larger qubit numbers. Here we use a cryogenic surface trap to integrate all necessary elements of the QCCD architecture—a scalable trap design, parallel interaction zones and fast ion transport—into a programmable trapped-ion quantum computer that has a system performance consistent with the low error rates achieved in the individual ion crystals. We apply this approach to realize a teleported CNOT gate using mid-circuit measurement6, negligible crosstalk error and a quantum volume7 of 26 = 64. These results demonstrate that the QCCD architecture provides a viable path towards high-performance quantum computers.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data presented in this manuscript are available from the corresponding author upon reasonable request.
References
Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Natl. Inst. Stand. Technol. 103, 259–328 (1998).
Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002).
Gaebler, J. P. et al. High-fidelity universal gate set for 9Be+ ion qubits. Phys. Rev. Lett. 117, 060505 (2016).
Ballance, C. J., Harty, T. P., Linke, N. M., Sepiol, M. A. & Lucas, D. M. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 117, 060504 (2016).
Christensen, J. E., Hucul, D., Campbell, W. C. & Hudson, E. R. High-fidelity manipulation of a qubit enabled by a manufactured nucleus. npj Quant. Inf. 6, 35 (2020).
Wan, Y. et al. Quantum gate teleportation between separated qubits in a trapped-ion processor. Science 364, 875–878 (2019).
Cross, A. W., Bishop, L. S., Sheldon, S., Nation, P. D. & Gambetta, J. M. Validating quantum computers using randomized model circuits. Phys. Rev. A 100, 032328 (2019).
Cirac, J. I. & Zoller, P. Quantum computations with cold trapped ions. Phys. Rev. Lett. 74, 4091–4094 (1995).
Monroe, C., Meekhof, D. M., King, B. E., Itano, W. M. & Wineland, D. J. Demonstration of a fundamental quantum logic gate. Phys. Rev. Lett. 75, 4714–4717 (1995).
Wang, Y. et al. Single-qubit quantum memory exceeding ten-minute coherence time. Nat. Photon. 11, 646–650 (2017).
Murali, P., Debroy, D. M., Brown, K. R. & Martonosi, M. Architecting noisy intermediate-scale trapped ion quantum computers. In 2020 ACM/IEEE 47th Annual International Symposium on Computer Architecture (ISCA) 529–542 (IEEE, 2020).
Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).
Hucul, D. et al. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 11, 37–42 (2015).
Home, J. P. et al. Complete methods set for scalable ion trap quantum information processing. Science 325, 1227–1230 (2009).
Kaufmann, H. et al. Scalable creation of long-lived multipartite entanglement. Phys. Rev. Lett. 119, 150503 (2017).
Lekitsch, B. et al. Blueprint for a microwave trapped ion quantum computer. Sci. Adv. 3, e1601540 (2017).
Labaziewicz, J. High Fidelity Quantum Gates with Ions in Cryogenic Microfabricated Ion Traps. PhD thesis, MIT (2008); http://web.mit.edu/cua/www/quanta/LabaziewiczThesis.pdf
Maunz, P. L. W. High Optical Access Trap 2.0. Report SAND2016–0796R https://prod-ng.sandia.gov/techlib-noauth/access-control.cgi/2016/160796r.pdf (Sandia National Laboratories, 2016).
Bowler, R. et al. Coherent diabatic ion transport and separation in a multizone trap array. Phys. Rev. Lett. 109, 080502 (2012).
Kaushal, V. et al. Shuttling-based trapped-ion quantum information processing. AVS Quantum Sci. 2, 014101 (2020).
Barrett, M. D. et al. Sympathetic cooling of 9Be+ and 24Mg+ for quantum logic. Phys. Rev. A 68, 042302 (2003).
Home, J. P. et al. Memory coherence of a sympathetically cooled trapped-ion qubit. Phys. Rev. A 79, 050305 (2009).
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
Palmero, M., Bowler, R., Gaebler, J. P., Leibfried, D. & Muga, J. G. Fast transport of mixed-species ion chains within a paul trap. Phys. Rev. A 90, 053408 (2014).
Home, J. P. & Steane, A. M. Electrode configurations for fast separation of trapped ions. Quantum Inf. Comput. 6, 289–325 (2006).
Splatt, F. et al. Deterministic reordering of 40Ca+ ions in a linear segmented Paul trap. New J. Phys. 11, 103008 (2009).
Haberman, N. Parallel Neighbor Sort (or the Glory of the Induction Principle). CMU Computer Science Report https://kilthub.cmu.edu/articles/journal_contribution/Parallel_neighbor-sort_or_the_glory_of_the_induction_principle_/6608258 (Carnegie Mellon University, 1979).
Sørensen, A. & Mølmer, K. Entanglement and quantum computation with ions in thermal motion. Phys. Rev. A 62, 022311 (2000).
Lee, P. J. et al. Phase control of trapped ion quantum gates. J. Opt. B 7, S371–S383 (2005).
Baldwin, C. H., Bjork, B. J., Gaebler, J. P., Hayes, D. & Stack, D. Subspace benchmarking high-fidelity entangling operations with trapped ions. Phys. Rev. Res. 2, 013317 (2020).
Viola, L., Knill, E. & Lloyd, S. Dynamical decoupling of open quantum systems. Phys. Rev. Lett. 82, 2417–2421 (1999).
Olmschenk, S. et al. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).
Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett. 106, 180504 (2011).
Monroe, C. et al. Resolved-sideband raman cooling of a bound atom to the 3D zero-point energy. Phys. Rev. Lett. 75, 4011–4014 (1995).
Jordan, E. et al. Near ground-state cooling of two-dimensional trapped-ion crystals with more than 100 ions. Phys. Rev. Lett. 122, 053603 (2019).
Gambetta, J. M. et al. Characterization of addressability by simultaneous randomized benchmarking. Phys. Rev. Lett. 109, 240504 (2012).
Barrett, M. et al. Deterministic quantum teleportation of atomic qubits. Nature 429, 737–739 (2004).
Negnevitsky, V. et al. Repeated multi-qubit readout and feedback with a mixed species trapped-ion register. Nature 563, 527–531 (2018).
Eisert, J., Jacobs, K., Papadopoulos, P. & Plenio, M. B. Optimal local implementation of nonlocal quantum gates. Phys. Rev. A 62, 052317 (2000).
McClean, J. R., Romero, J., Babbush, R. & Aspuru-Guzik, A. The theory of variational hybrid quantum-classical algorithms. New J. Phys. 18, 023023 (2016).
Farhi, E. & Goldstone, J. A quantum approximate optimization algorithm. Preprint at https://arxiv.org/abs/1411.4028 (2014).
Aaronson, S. & Chen, L. Complexity-theoretic foundations of quantum supremacy experiments. Preprint at https://arxiv.org/abs/1612.05903 (2016).
Jucevic, P. et al. Demonstration of quantum volume 64 on a superconducting quantum computing system. Preprint at https://arxiv.org/abs/2008.08571 (2020).
van Mourik, M. W. et al. Coherent rotations of qubits within a a surface ion-trap quantum computer. Phys. Rev. A 102, 022611 (2020).
Mount, E. et al. Single qubit manipulation in a microfabricated surface electrode ion trap. New J. Phys. 15, 093018 (2013).
Mehta, K. K. et al. Integrated optical multi-ion quantum logic. Nature 586, 533–537 (2020).
Kovalev, A. A. & Pryadko, L. P. Quantum kronecker sum-product low-density parity-check codes with finite rate. Phys. Rev. A 88, 012311 (2013).
Blakestad, R. B. Transport of Trapped-ion Qubits within a Scalable Quantum Processor. PhD thesis, Univ. of Colorado (2010); https://www.nist.gov/system/files/documents/2017/05/09/blakestad2010thesis.pdf.
Biercuk, M. J., Doherty, A. C. & Uys, H. Dynamical decoupling sequence construction as a filter-design problem. J. Phys. B 44, 154002 (2011).
Harper, R., Flammia, S. T. & Wallman, J. J. Efficient learning of quantum noise. Nat. Phys. 16, 1184–1188 (2020).
Meier, A. M. Randomized Benchmarking of Clifford Operators. PhD thesis, Univ. of Colorado (2006); https://arxiv.org/abs/1811.10040
Hofmann, H. F. Complementary classical fidelities as an efficient criterion for the evaluation of experimentally realized quantum operations. Phys. Rev. Lett. 94, 160504 (2005).
Nielsen, M. A. A simple formula for the average gate fidelity of a quantum dynamical operation. Phys. Lett. A 303, 249–252 (2002).
Abraham, H. et al. Qiskit: an Open-Source Framework for Quantum Computing https://zenodo.org/record/2562111#.YC6b8n7LdaR (2019).
Acknowledgements
This work was made possible by a large group of people, and we thank the entire Honeywell Quantum Solutions team for their many contributions.
Author information
Authors and Affiliations
Contributions
J.M.P., J.M.D., C.F., J.P.G., S.A.M., M.S.A. and B.N. all contributed to the experimental design, construction and data collection. C.H.B. and K.M. contributed to the theory, quantum circuit design and data analysis. All authors contributed to this manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Extended data
is available for this paper at https://doi.org/10.1038/s41586-021-03318-4.
Peer review information Nature thanks Winfried Hensinger and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
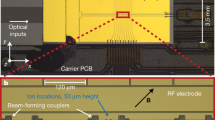
Extended Data Fig. 1 System details.
a, Close-up schematic of the trap region used in this work. Dimensions are in micrometres. We refer to the orange gating region on the left as zone 1 and the blue gating region as zone 2. b, Transport primitive library and associated heating estimates. For the estimates, we fit four ion-crystal spin-flip data to a model that assumes that all modes are at the same temperature. The fitted temperature increases are converted to units of quanta/mode (we note that the inequality holds for all modes). The times shown do not include interpolation between different operations or small delays in the electronics, which increase the time for every operation by ~10%. The interzone shift is a linear shift between the two gate zones, whereas an intrazone shift moves ions within a single gate zone by 110 μm for single-qubit addressing. c, Times for qubit operations, transport and cooling. Circuits can be run using two different measurement protocols. For circuits in which all measurements are made at the end, we use the high-fidelity measurement setting. Circuits containing mid-circuit measurements use shorter-duration measurements to minimize the crosstalk error on idle qubits. The shorter detection time measurement error is ~7 × 10−3, about twice as large as those reported in Table 1. Mid-circuit measurements induce an error of ~1% on neighbouring idle qubits, as measured by a Ramsey experiment. There are three different cooling stages used during transport (stages 1 and 2) and before gates (stage 3) and are either implemented through Doppler or sideband (SB) cooling. d, Construction of a phase-insensitive TQ gate. The Mølmer–Sørensen interaction generates the unitary \({U}_{{\rm{MS}}}=\exp [-{\rm{i}}\frac{{\rm{\pi }}}{4}{(X\sin \varphi +Y\cos \varphi )}^{\otimes 2}]\) (orange), whose basis is determined by the optical phase ϕ. SQ operations driven by the same laser beams generate the unitary \({U}_{{\rm{SQ}}}=\exp [-{\rm{i}}\frac{{\rm{\pi }}}{4}(X\cos \,\varphi +Y\sin \,\varphi )]\) (blue) and are applied globally to both qubits. The resulting composite gate is, up to a global phase, given by \({U}_{zz}=\exp (-{\rm{i}}\frac{{\rm{\pi }}}{4}Z\otimes Z)\) (green).
Extended Data Fig. 2 Estimated gate errors and randomized benchmarking results.
a, SQ RB for all four qubits. b, TQ RB results for zone 1. c, TQ RB results for zone 2. d, An estimated error budget for a single TQ gate operation. e, Correlation parameters for simultaneous TQ RB. Each square represents a value of δi,j with the numbers being scaled by 10−4. All are within one standard deviation of zero. f, Addressability error estimates for simultaneous RB. The quantities \({\alpha }_{z}^{{\rm{both}}}\) and γz refer to simultaneous RB decay rates and their deviation from individual RB decay rates, as described in the text.
Extended Data Fig. 3 Teleported CNOT gate experiment results.
a, Circuit implementing a teleported CNOT gate, with q0 and q3 the control and target qubit, respectively. b, Bar plots showing the distribution of measurement outcomes when qubits q0 and q3 are prepared and measured in the {|0⟩, |1⟩} and {|+⟩, |−⟩} bases. c, The teleported CNOT gate time budget.
Extended Data Fig. 4 QV N = 4 results.
a, Example of the transport operations needed for part of an N = 4 QV circuit. Trap regions are labelled as load zone (L); auxiliary zone 1 (A1); gate zone 1, left (G1L); gate zone 1, centre (G1C); gate zone 1, right (G1R); auxiliary zone 2 (A2); gate zone 2, left (G2L); gate zone 2, centre (G2C); and gate zone 2, right (G2R). b, An N = 4 QV circuit time budget.
Rights and permissions
About this article
Cite this article
Pino, J.M., Dreiling, J.M., Figgatt, C. et al. Demonstration of the trapped-ion quantum CCD computer architecture. Nature 592, 209–213 (2021). https://doi.org/10.1038/s41586-021-03318-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03318-4
This article is cited by
-
Protecting expressive circuits with a quantum error detection code
Nature Physics (2024)
-
Rapid exchange cooling with trapped ions
Nature Communications (2024)
-
Theoretical guarantees for permutation-equivariant quantum neural networks
npj Quantum Information (2024)
-
Multi-site integrated optical addressing of trapped ions
Nature Communications (2024)
-
Penning micro-trap for quantum computing
Nature (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.