Abstract
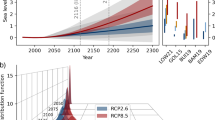
The land ice contribution to global mean sea level rise has not yet been predicted1 using ice sheet and glacier models for the latest set of socio-economic scenarios, nor using coordinated exploration of uncertainties arising from the various computer models involved. Two recent international projects generated a large suite of projections using multiple models2,3,4,5,6,7,8, but primarily used previous-generation scenarios9 and climate models10, and could not fully explore known uncertainties. Here we estimate probability distributions for these projections under the new scenarios11,12 using statistical emulation of the ice sheet and glacier models. We find that limiting global warming to 1.5 degrees Celsius would halve the land ice contribution to twenty-first-century sea level rise, relative to current emissions pledges. The median decreases from 25 to 13 centimetres sea level equivalent (SLE) by 2100, with glaciers responsible for half the sea level contribution. The projected Antarctic contribution does not show a clear response to the emissions scenario, owing to uncertainties in the competing processes of increasing ice loss and snowfall accumulation in a warming climate. However, under risk-averse (pessimistic) assumptions, Antarctic ice loss could be five times higher, increasing the median land ice contribution to 42 centimetres SLE under current policies and pledges, with the 95th percentile projection exceeding half a metre even under 1.5 degrees Celsius warming. This would severely limit the possibility of mitigating future coastal flooding. Given this large range (between 13 centimetres SLE using the main projections under 1.5 degrees Celsius warming and 42 centimetres SLE using risk-averse projections under current pledges), adaptation planning for twenty-first-century sea level rise must account for a factor-of-three uncertainty in the land ice contribution until climate policies and the Antarctic response are further constrained.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All global climate, simple climate, ice sheet and glacier model data used as inputs to this study are provided with the code as described above. Main and risk-averse projections at 2100 from the analysis are provided in Supplementary Information for each of the 23 regions, and the Antarctic, glacier and land ice sums.
Code availability
R code and input data are available at https://github.com/tamsinedwards/emulandice. Each simulation in the sea level projections file has a label in the ‘publication’ column for the reference (Goelzer20206, Seroussi20207, Payne20218 or Marzeion20205), or ‘New’ if previously unpublished.
References
Oppenheimer, M. et al. Sea Level Rise and Implications for Low-Lying Islands, Coasts and Communities. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds Pörtner, H.-O. et al.) (IPCC, 2019).
Nowicki, S. M. J. et al. Ice Sheet Model Intercomparison Project (ISMIP6) contribution to CMIP6. Geosci. Model Dev. 9, 4521–4545 (2016).
Nowicki, S. et al. Experimental protocol for sea level projections from ISMIP6 stand-alone ice sheet models. Cryosphere 14, 2331–2368 (2020).
Hock, R. et al. GlacierMIP – a model intercomparison of global-scale glacier mass-balance models and projections. J. Glaciol. 65, 453–467 (2019).
Marzeion, B. et al. Partitioning the uncertainty of ensemble projections of global glacier mass change. Earth’s Future 8, e2019EF001470 (2020).
Goelzer, H. et al. The future sea-level contribution of the Greenland ice sheet: a multi-model ensemble study of ISMIP6. Cryosphere 14, 3071–3096 (2020).
Seroussi, H. et al. ISMIP6 Antarctica: a multi-model ensemble of the Antarctic ice sheet evolution over the 21st century. Cryosphere 14, 3033–3070 (2020).
Payne, A. et al. Future sea level change under CMIP5 and CMIP6 scenarios from the Greenland and Antarctic ice sheets. Geophys. Res. Lett. (in the press).
van Vuuren, D. P. et al. The representative concentration pathways: an overview. Clim. Change 109, 5–31 (2011).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012).
Riahi, K. et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: an overview. Glob. Environ. Change 42, 153–168 (2017).
McKenna, C. M. et al. Stringent mitigation substantially reduces risk of unprecedented near-term warming rates. Nat. Clim. Change 11, 126–131 (2021).
Eyring, V. et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Goelzer, H. et al. Design and results of the ice sheet model initialisation experiments initMIP-Greenland: an ISMIP6 intercomparison. Cryosphere 12, 1433–1460 (2018).
Seroussi, H. et al. initMIP-Antarctica: an ice sheet model initialization experiment of ISMIP6. Cryosphere 13, 1441–1471 (2019).
Slater, D. A. et al. Estimating Greenland tidewater glacier retreat driven by submarine melting. Cryosphere 13, 2489–2509 (2019).
Slater, D. A. et al. Twenty-first-century ocean forcing of the Greenland ice sheet for modelling of sea level contribution. Cryosphere 14, 985–1008 (2020).
Favier, L. et al. Assessment of sub-shelf melting parameterisations using the ocean–ice-sheet coupled model NEMO(v3.6)–Elmer/Ice(v8.3). Geosci. Model Dev. 12, 2255–2283 (2019).
Jourdain, N. C. et al. A protocol for calculating basal melt rates in the ISMIP6 Antarctic ice sheet projections. Cryosphere 14, 3111–3134 (2020).
Goelzer, H. et al. Remapping of Greenland ice sheet surface mass balance anomalies for large ensemble sea-level change projections. Cryosphere 14, 1747–1762 (2020).
Barthel, A. et al. CMIP5 model selection for ISMIP6 ice sheet model forcing: Greenland and Antarctica. Cryosphere 14, 855–879 (2020).
O’Neill, B. C. et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 9, 3461–3482 (2016).
Andrianakis, I. & Challenor, P. G. The effect of the nugget on Gaussian process emulators of computer models. Comput. Stat. Data Anal. 56, 4215–4228 (2012).
Gramacy, R. B. & Lee, H. K. H. Cases for the nugget in modeling computer experiments. Stat. Comput. 22, 713–722 (2012).
Edwards, T. L. et al. Revisiting Antarctic ice loss due to marine ice cliff instability. Nature 566, 58–64 (2019).
Church, J. A. et al. Sea level change. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (eds Stocker, T. F. et al.) Ch. 13 (Cambridge Univ. Press, 2013).
Levermann, A. et al. Projecting Antarctica’s contribution to future sea level rise from basal ice shelf melt using linear response functions of 16 ice sheet models (LARMIP-2). Earth Syst. Dynam 11, 35–76 (2020).
Bulthuis, K. et al. Uncertainty quantification of the multi-centennial response of the Antarctic ice sheet to climate change. Cryosphere 13, 1349–1380 (2019).
Nauels, A. et al. Synthesizing long-term sea level rise projections – the MAGICC sea level model v2.0. Geosci. Model Dev. 10, 2495–2524 (2017).
Palmer, M. D. et al. Exploring the drivers of global and local sea‐level change over the 21st century and beyond. Earth’s Future 8, e2019EF001413 (2020).
Biemans, H. et al. Importance of snow and glacier meltwater for agriculture on the Indo-Gangetic Plain. Nature Sustain. 2, 594–601 (2019).
Forster, P. M., Maycock, A. C., McKenna, C. M. & Smith, C. J. Latest climate models confirm need for urgent mitigation. Nat. Clim. Change 10, 7–10 (2019).
Meehl, G. et al. Context for interpreting equilibrium climate sensitivity and transient climate response from the CMIP6 Earth system models. Sci. Adv. 6, eaba1981 (2020).
Meredith, M. et al. Polar Regions. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate (eds Pörtner, H.-O. et al.) Ch. 3 (2019).
Naughten, K. A. et al. Future projections of Antarctic ice shelf melting based on CMIP5 scenarios. J. Clim. 31, 5243–5261 (2018).
Mottram, R. et al. What is the surface mass balance of Antarctica? An intercomparison of regional climate model estimates. Preprint at https://doi.org/10.5194/tc-2019-333 (2020).
Roussel, M.-L., Lemonnier, F., Genthon, C. & Krinner, G. Evaluating Antarctic precipitation in ERA5 and CMIP6 against CloudSat observations. Cryosphere 14, 2715–2727 (2020).
Reese, R. et al. The role of history and strength of the oceanic forcing in sea level projections from Antarctica with the Parallel Ice Sheet Model. Cryosphere 14, 3097–3110 (2020).
Golledge, N. R. et al. The multi-millennial Antarctic commitment to future sea-level rise. Nature 526, 421–425 (2015).
Golledge, N. R. et al. Global environmental consequences of twenty-first-century ice-sheet melt. Nature 566, 65–72 (2019).
DeConto, R. M. & Pollard, D. Contribution of Antarctica to past and future sea-level rise. Nature 531, 591–597 (2016).
Clerc, F., Minchew, B. M. & Behn, M. D. Marine ice cliff instability mitigated by slow removal of ice shelves. Geophys. Res. Lett. 46, 12108–12116 (2019).
Williamson, D. B. & Sansom, P. G. How are emergent constraints quantifying uncertainty and what do they leave behind? Bull. Am. Meterol. Soc. 100, 2571–2588 (2019).
Farinotti, D. et al. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 12, 168–173 (2019).
Trusel, L. D. et al. Divergent trajectories of Antarctic surface melt under two twenty-first-century climate scenarios. Nat. Geosci. 8, 927–932 (2015).
Bell, R. E. et al. Antarctic ice shelf potentially stabilized by export of meltwater in surface river. Nature 544, 344–348 (2017).
O’Hagan, A. Bayesian analysis of computer code outputs: a tutorial. Reliab. Eng. Syst. Saf. 91, 1290–1300 (2006).
Gu, M. et al. RobustGaSP: robust Gaussian stochastic process emulation in R. R J. 11, 112–136 (2019).
Gu, M., Wang, X. & Berger, J. O. Robust Gaussian stochastic process emulation. Ann. Stat. 46, 3038–3066 (2018).
van Beers, W. C. M. & Kleijnen, J. P. C. Kriging for interpolation in random simulation. J. Oper. Res. Soc. 54, 255–262 (2003).
Salter, J. M. & Williamson, D. A comparison of statistical emulation methodologies for multi-wave calibration of environmental models. Environmetrics 27, 507–523 (2016).
Williamson, D. & Blaker, A. T. Evolving Bayesian emulators for structured chaotic time series, with application to large climate models. SIAM/ASA J. Uncertain. Quant. 2, 1–28 (2014).
Williamson, D., Blaker, A., Hampton, C. & Salter, J. Identifying and removing structural biases in climate models with history matching. Clim. Dyn. 45, 1299–1324 (2015).
Araya-Melo, P. A., Crucifix, M. & Bounceur, N. Global sensitivity analysis of the Indian monsoon during the Pleistocene. Clim. Past 11, 45–61 (2015).
Bounceur, N., Crucifix, M. & Wilkinson, R. D. Global sensitivity analysis of the climate–vegetation system to astronomical forcing: an emulator-based approach. Earth Syst. Dynam. 6, 205–224 (2015).
Lord, N. S. et al. Emulation of long-term changes in global climate: application to the late Pliocene and future. Clim. Past 13, 1539–1571 (2017).
Bowman, K. W. et al. A hierarchical statistical framework for emergent constraints: application to snow–albedo feedback. Geophys. Res. Lett. 45, 13050–13059 (2018).
Nowicki, S. et al. Insights into spatial sensitivities of ice mass response to environmental change from the SeaRISE ice sheet modeling project. I: Antarctica. J. Geophys. Res. Earth 118, 1002–1024 (2013).
Nowicki, S. et al. Insights into spatial sensitivities of ice mass response to environmental change from the SeaRISE ice sheet modeling project. II: Greenland. J. Geophys. Res. Earth 118, 1025–1044 (2013).
Saito, F., Abe-Ouchi, A., Takahashi, K. & Blatter, H. SeaRISE experiments revisited: potential sources of spread in multi-model projections of the Greenland ice sheet. Cryosphere 10, 43–63 (2016).
Rougier, J., Sexton, D. M. H., Murphy, J. M. & Stainforth, D. A. Analyzing the climate sensitivity of the HadSM3 climate model using ensembles from different but related experiments. J. Clim. 22, 3540–3557 (2009).
Bastos, L. S. & O’Hagan, A. Diagnostics for Gaussian process emulators. Technometrics 51, 425–438 (2009).
Silverman, B. W. Density Estimation (Chapman and Hall, 1986).
The IMBIE Team. Mass balance of the Greenland Ice Sheet from 1992 to 2018. Nature 579, 233–239 (2020).
The IMBIE Team. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 558, 219–222 (2018).
Price, S. F., Payne, A. J., Howat, I. M. & Smith, B. E. Committed sea-level rise for the next century from Greenland ice sheet dynamics during the past decade. Proc. Natl Acad. Sci. USA 108, 8978–8983 (2011).
Alevropoulos-Borrill, A. V., Nias, I. J., Payne, A. J., Golledge, N. R. & Bingham, R. J. Ocean-forced evolution of the Amundsen Sea catchment, West Antarctica, by 2100. Cryosphere 14, 1245–1258 (2020).
Acknowledgements
We thank J. Rougier for providing advice and support throughout, and writing the original random effects model. We also thank B. Fox-Kemper, H. Hewitt, R. Kopp, S. Drijfhout and J. Rohmer for discussions, suggestions and support. We thank N. Barrand, W. Chang, V. Volodina and D. Williamson for their thorough and constructive comments, which greatly improved the manuscript. We thank the Climate and Cryosphere (CliC) Project, which provided support for ISMIP6 and GlacierMIP through sponsoring of workshops, hosting the websites and ISMIP6 wiki, and promotion. We acknowledge the World Climate Research Programme, which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP5 and CMIP6. We thank the climate modelling groups for producing and making available their model output, the Earth System Grid Federation (ESGF) for archiving the CMIP data and providing access, the University at Buffalo for ISMIP6 data distribution and upload, and the multiple funding agencies who support CMIP5 and CMIP6 and ESGF. We thank the ISMIP6 steering committee, the ISMIP6 model selection group and the ISMIP6 dataset preparation group for their continuous engagement in defining ISMIP6. This is ISMIP6 contribution no. 13. This publication was supported by PROTECT, which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 869304. This is PROTECT contribution number 12. T.L.E. was supported by PROTECT and the UK Natural Environment Research Council grant NE/T007443/1. F.T. was supported by PROTECT. J.F.O’N. was supported by the UK Natural Environment Research Council London Doctoral Training Partnership. R. Gladstone’s contribution was supported by Academy of Finland grants 286587 and 322430, and T. Zwinger’s by grant 322430. W.H.L. and G.R.L. were supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Science Foundation under Cooperative Agreement no. 1852977. Computing and data storage resources for CISM simulations, including the Cheyenne supercomputer (https://doi.org/10.5065/D6RX99HX), were provided by the Computational and Information Systems Laboratory (CISL) at NCAR. Support for X.A.-D., M.J.H., S.F.P. and T. Zhang was provided through the Scientific Discovery through Advanced Computing (SciDAC) programme funded by the US Department of Energy (DOE), Office of Science, Advanced Scientific Computing Research and Biological and Environmental Research programmes. N.R.G., D.P.L. and B.A. were supported by New Zealand Ministry for Business, Innovation and Employment contracts RTUV1705 (‘NZSeaRise’) and ANTA1801 (‘Antarctic Science Platform’). J.M.G. and R.S.S. were supported by the National Centre for Atmospheric Science, funded by the UK National Environment Research Council. R. Calov was funded by the PalMod project of the Bundesministerium für Bildung und Forschung (BMBF) with the grants FKZ 01LP1502C and 01LP1504D. D.F.M. and C.S. were supported by the Director, Office of Science, Offices of Advanced Scientific Computing Research (ASCR) and Biological and Environmental Research (BER), of the US Department of Energy under contract no. DE-AC02-05CH11231, as a part of the ProSPect SciDAC Partnership. BISICLES simulations used resources of the National Energy Research Scientific Computing Center (NERSC), a US Department of Energy Office of Science User Facility operated under contract no. DE-AC02-05CH11231. C.Z. and B.K.G.-F. were supported under the Australian Research Council’s Special Research Initiative for Antarctic Gateway Partnership (project ID SR140300001) and received grant funding from the Australian Government for the Australian Antarctic Program Partnership (project ID ASCI000002). Work was performed by E.L., N.-J.S. and H.S. at the California Institute of Technology’s Jet Propulsion Laboratory under a contract with the National Aeronautics and Space Administration; support was provided by grants from NASA’s Cryospheric Science, Sea Level Change Team, and Modeling, Analysis and Prediction (MAP) programmes. They acknowledge computational resources and support from the NASA Advanced Supercomputing Division. The CMIP5 and CMIP6 projection data were processed by C.M.M. with funding from the European Union’s CONSTRAIN project as part of the Horizon 2020 Research and Innovation Programme under grant agreement number 820829. A. Barthel was supported by the DOE Office of Science HiLAT-RASM project and Early Career Research programme. T.A. and R.W. are supported by the Deutsche Forschungsgemeinschaft (DFG) in the framework of the priority programme ‘Antarctic research with comparative investigations in Arctic ice areas’ by grants WI4556/2-1 and WI4556/4-1, and within the framework of the PalMod project (FKZ: 01LP1925D) supported by the German Federal Ministry of Education and Research (BMBF) as a Research for Sustainability initiative (FONA). R.R. is supported by the Deutsche Forschungsgemeinschaft (DFG) by grant WI4556/3-1 and through the TiPACCs project that receives funding from the European Union’s Horizon 2020 Research and Innovation programme under grant agreement no. 820575. Development of PISM is supported by NASA grant NNX17AG65G and NSF grants PLR-1603799 and PLR-1644277. The authors gratefully acknowledge the European Regional Development Fund (ERDF), the German Federal Ministry of Education and Research and the Land Brandenburg for supporting this project by providing resources for the high-performance computer system at the Potsdam Institute for Climate Impact Research. Computer resources for this project have also been provided by the Gauss Centre for Supercomputing, Leibniz Supercomputing Centre (http://www.lrz.de, last access: 16 July 2020) under project IDs pr94ga and pn69ru. R. Greve and C.C. were supported by Japan Society for the Promotion of Science (JSPS) KAKENHI grant nos JP16H02224 and JP17H06323. R. Greve was supported by JSPS KAKENHI grant no. JP17H06104, by a Leadership Research Grant of Hokkaido University’s Institute of Low Temperature Science (ILTS), and by the Arctic Challenge for Sustainability (ArCS, ArCS II) project of the Japanese Ministry of Education, Culture, Sports, Science and Technology (MEXT) (programme grant nos JPMXD1300000000, JPMXD1420318865). F.P. and S. Sun were supported by the MIMO project within the STEREO III programme of the Belgian Science Policy Office, contract SR/00/336 and the Fonds de la Recherche Scientifique (FNRS) and the Fonds Wetenschappelijk Onderzoek-Vlaanderen (FWO) under the EOS project no. O0100718F. A. Shepherd was supported by the UK Natural Environment Research Council in partnership with the Centre for Polar Observation and Modelling and the British Antarctic Survey and by the European Space Agency Climate Change Initiative. D.F. was supported by an appointment to the NASA Postdoctoral Program at the NASA Goddard Space Flight Center, administered by Universities Space Research Association under contract with NASA. R.v.d.W. acknowledges the support of the Future Deltas programme of Utrecht University. C.J.S. was supported by a NERC/IIASA Collaborative Research Fellowship (NE/T009381/1). H.G. has received funding from the programme of the Netherlands Earth System Science Centre (NESSC), financially supported by the Dutch Ministry of Education, Culture and Science (OCW) under grant no. 024.002.001 and from the Research Council of Norway under projects INES (270061) and KeyClim (295046). F.S. acknowledges support from DOE Office of Science grant no. DE-SC0020073. High-performance computing and storage resources were provided by the Norwegian Infrastructure for Computational Science through projects NN9560K, NN9252K, NS9560K, NS9252K and NS5011K.
Author information
Authors and Affiliations
Contributions
T.L.E. conceived the idea, carried out all statistical analysis except the random effects model, produced the figures, and wrote the manuscript. S.N. led ISMIP6, including experimental design, organization and analysis, and provided scientific interpretation. B.M. and R.H. co-led GlacierMIP and contributed simulations (below), and provided data and interpretation. H.G. and H.S. led the processing and analysis in ISMIP6 for the Greenland and Antarctic ice sheets, respectively, contributed simulations (below), and provided scientific interpretation and advice. N.C.J. and. D.A.S. co-derived with T.L.E. the ice sheet continuous parameter distributions for the emulator, and also derived the corresponding ocean forcing parameterization studies with X.A.-D., F.S. and T.H. for Antarctica and with F.S., D.F. and M.M. for Greenland. F.T. performed the random effects model cross-check for Antarctica. C.J.S. provided the FaIR projections and C.M.M. provided the CMIP5 and CMIP6 projection data for the emulator. E.S. led the ISMIP6 data processing. A.A.-O., J.M.G., E.L., W.H.L., A.J.P., A. Shepherd contributed to the ISMIP6 experimental design, organization and analysis as members of its steering committee, and R.S.S. and W.H.L. led the ISMIP6 atmosphere focus group. C.M.L., A. Barthel and C.A. selected the CMIP5 models for ISMIP6, X.F. and P.A. ran the surface mass balance model for the Greenland and R. Cullather prepared the Antarctic surface mass balance, and L.D.T. and M.v.d.B. provided the ice shelf collapse forcing. For Antarctica: T.K. and A.H. contributed the AWI/PISM simulations; M.J.H., T. Zhang and S.F.P. contributed the DOE/MALI simulations; R. Greve and R. Calov contributed the ILTS_PIK/SICOPOLIS simulations; H.G. and R.v.d.W. contributed the IMAU/IMAUICE simulations; N.-J.S. and H.S. contributed the JPL/ISSM simulations; C.D. and A.Q. contributed the LSCE/GRISLI simulations; G.R.L. and W.H.L. contributed the NCAR/CISM simulations; R.R., T.A. and R.W. contributed the PIK/PISM simulations; T.P., M.M. and H.S. contributed the UCIJPL/ISSM simulations; F.P. and S. Sun contributed the ULB/fETISh simulations; C.Z., R. Gladstone, B.K.G.-F. and T. Zwinger contributed the UTAS/Elmer/Ice simulations; J.V.B. and P.H. contributed the VUB/AISMPALEO simulations; N.R.G. and D.P.L. contributed the VUW/PISM simulations; and D.F.M., C. Shafer and J.F.O’N. contributed the CPOM/BISICLES simulations. For Greenland: M.R. and A.H. contributed the AWI/ISSM simulations; V.L. and A.J.P. contributed the BGC/BISICLES simulations; I.N., D.F. and S.N. contributed the GSFC/ISSM simulations; R. Greve, R. Calov and C.C. contributed the ILTS_PIK/SICOPOLIS simulations; H.G., R.v.d.W. and M.v.d.B. contributed the IMAU/IMAUICE simulations; N.-J.S. and H.S. contributed the JPL/ISSM simulations; J.C. and N.-J.S. contributed the JPL/ISSMPALEO simulations; A.Q. and C.D. contributed the LSCE/GRISLI simulations; L.T. contributed the MUN/GSM simulations; W.H.L. and G.R.L. contributed the NCAR/CISM simulations; A.A. contributed the UAF/PISM simulations; Y.C., H.S. and M.M. contributed the UCIJPL/ISSM simulations; S.L.c. and P.H. contributed the VUB/GISM simulations; and D.P.L. and N.R.G. contributed the VUW/PISM simulations. For global glaciers: B.A. contributed the AND2012 simulations; K.F. and A. Sakai contributed the GLIMB simulations; M. Huss contributed the GloGEM simulations; H.Z. contributed the GloGEMflow simulations; S. Shannon contributed the JULES simulations; P.K. and W.I. contributed the KRA2017 simulations; B.M. and J.-H.M. contributed the MAR2012 simulations; F.M. and N.C. contributed the OGGM simulations; D.R.R. and R.H. contributed the PyGEM simulations; A. Bliss and V.R. contributed the RAD2014 simulations; R.v.d.W. contributed the WAL2001 simulations; and A. Bliss and J.-H.M. assisted with data handling. All authors contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Nicholas Barrand, Won Chang, Victoria Volodina, Daniel Williamson and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Emulator leave-one-out validation for ice sheets and eight glacier regions.
a–l, Left: emulator predictions versus simulations for each regional sea level contribution in the year 2100, with percentage of predictions falling outside ±2 emulator standard deviations and mean absolute error in cm SLE. Right: standardized residuals (emulated minus simulated, divided by emulator standard deviation). Predictions falling outside ±2 emulator standard deviations are shown in orange.
Extended Data Fig. 2 Emulator leave-one-out validation for 11 glacier regions.
As for Extended Data Fig. 1, but for the remaining glacier emulators.
Extended Data Fig. 3 Temperature projections for 2015–2100 from FaIR and CMIP6 ensembles.
a, b, Global surface air temperature projections under different greenhouse gas scenarios (see text) from the FaIR simple climate model ensemble (a; N = 5,000; same as Fig. 3a), and CMIP6 global climate model ensemble (b; N ≈ 30 models per scenario; see Methods) sampled with a kernel density estimate (N = 1,000).
Extended Data Fig. 4 Sensitivity of ice sheet projections at 2100 under SSP5-85 to uncertain inputs.
a, Greenland. b, West Antarctica. c, East Antarctica. d, Antarctic Peninsula. Box and whiskers show [5, 25, 50, 75, 95]th percentiles. Indices refer to test (see Extended Data Table 3). Sensitivity test 1, default; 2, CMIP6 global climate model ensemble projections of global mean surface air temperature, instead of FaIR simple climate model; 3, fixed global mean surface air temperature; 4, fixed glacier retreat (Greenland) or basal melt (Antarctica) parameter. Antarctic regions only: basal melt parameter has sensitivity test 5: ‘mean Antarctic’ distribution; 6, ‘Pine Island Glacier’ distribution; 7, uniform, high distribution; 8, uniform, very high distribution. Ice shelf collapse scenario: sensitivity test 9, off; 10, on. 11, Risk-averse projections using the high ‘Pine Island Glacier’ distribution for basal melt (test 6), ice shelf collapse on (test 10), and the ice sheet and climate models that give the highest sea level contributions (Extended Data Fig. 5; test 6, 7).
Extended Data Fig. 5 Robustness of ice sheet projections under NDCs to ice sheet/climate model simulation selection and treatment.
a, Greenland. b, West Antarctica. c, East Antarctica. d, Antarctic Peninsula. Box and whiskers show [5, 25, 50, 75, 95]th percentiles. Indices refer to test (see Extended Data Table 4). Robustness test 1, default; 2, higher-resolution ice sheet models; 3, ice sheet models with the most complete sampling of uncertainties (10 models for Greenland, four for Antarctica); 4, single ice sheet model with the most complete sampling of uncertainties and (coincidentally) high sensitivity to retreat or basal melting parameter. Antarctic regions only: robustness test 5, alternative single ice sheet model with nearly as complete sampling but low sensitivity to basal melt parameter; 6, ice sheet models with the highest sensitivity to basal melt parameter; 7, climate models that lead to highest sea level contributions. 8, ice sheet models with 2015–2020 mass change in the range 0–0.6 cm SLE; 9, only ice sheet models that use the standard ISMIP melt parameterizations; 10, higher basal melt value assigned to ice sheet models that do not use the standard ISMIP6 melt parameterizations.
Extended Data Fig. 6 Sensitivity to basal melting by Antarctic ice sheet and climate model.
Vertical lines show ice sheet models that do not use the ISMIP6 basal melt parameterization, and the basal melt value they are assigned. Ice sheet models include the high and low sensitivity models in Extended Data Fig. 5: test 4 (ILTS_PIK/SICOPOLIS) and test 5 (LSCE/GRISLI).
Extended Data Fig. 7 Effect of Antarctic ice shelf collapse by climate model.
Additional sea level contribution at 2100 when using ice shelf collapse for six climate models, ordered by maximum impact on the Peninsula contribution. a, West Antarctica, b, East Antarctica and c, Antarctic Peninsula.
Supplementary information
Supplementary Information
Timeseries of projections provided as Comma Separated Value (CSV) files, and screen-readable versions of Extended Data Tables 3 and 4.
Rights and permissions
About this article
Cite this article
Edwards, T.L., Nowicki, S., Marzeion, B. et al. Projected land ice contributions to twenty-first-century sea level rise. Nature 593, 74–82 (2021). https://doi.org/10.1038/s41586-021-03302-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03302-y
This article is cited by
-
Warming-induced hydrothermal anomaly over the Earth’s three Poles amplifies concurrent extremes in 2022
npj Climate and Atmospheric Science (2024)
-
Ross Gyre variability modulates oceanic heat supply toward the West Antarctic continental shelf
Communications Earth & Environment (2024)
-
Sustained ocean cooling insufficient to reverse sea level rise from Antarctica
Communications Earth & Environment (2024)
-
A framework for estimating the anthropogenic part of Antarctica’s sea level contribution in a synthetic setting
Communications Earth & Environment (2024)
-
Sea-level rise induced change in exposure of low-lying coastal land: implications for coastal conservation strategies
Anthropocene Coasts (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.