Abstract
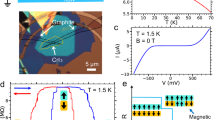
Moiré superlattices1,2 have recently emerged as a platform upon which correlated physics and superconductivity can be studied with unprecedented tunability3,4,5,6. Although correlated effects have been observed in several other moiré systems7,8,9,10,11,12,13,14,15,16,17, magic-angle twisted bilayer graphene remains the only one in which robust superconductivity has been reproducibly measured4,5,6. Here we realize a moiré superconductor in magic-angle twisted trilayer graphene (MATTG)18, which has better tunability of its electronic structure and superconducting properties than magic-angle twisted bilayer graphene. Measurements of the Hall effect and quantum oscillations as a function of density and electric field enable us to determine the tunable phase boundaries of the system in the normal metallic state. Zero-magnetic-field resistivity measurements reveal that the existence of superconductivity is intimately connected to the broken-symmetry phase that emerges from two carriers per moiré unit cell. We find that the superconducting phase is suppressed and bounded at the Van Hove singularities that partially surround the broken-symmetry phase, which is difficult to reconcile with weak-coupling Bardeen–Cooper–Schrieffer theory. Moreover, the extensive in situ tunability of our system allows us to reach the ultrastrong-coupling regime, characterized by a Ginzburg–Landau coherence length that reaches the average inter-particle distance, and very large TBKT/TF values, in excess of 0.1 (where TBKT and TF are the Berezinskii–Kosterlitz–Thouless transition and Fermi temperatures, respectively). These observations suggest that MATTG can be electrically tuned close to the crossover to a two-dimensional Bose–Einstein condensate. Our results establish a family of tunable moiré superconductors that have the potential to revolutionize our fundamental understanding of and the applications for strongly coupled superconductivity.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the current study are available from the corresponding authors upon reasonable and well motivated request.
References
Suárez Morell, E., Correa, J. D., Vargas, P., Pacheco, M. & Barticevic, Z. Flat bands in slightly twisted bilayer graphene: tight-binding calculations. Phys. Rev. B 82, 121407 (2010).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).
Burg, G. W. et al. Correlated insulating states in twisted double bilayer graphene. Phys. Rev. Lett. 123, 197702 (2019).
Shen, C. et al. Correlated states in twisted double bilayer graphene. Nat. Phys. 16, 520–525 (2020).
Cao, Y. et al. Tunable correlated states and spin-polarized phases in twisted bilayer–bilayer graphene. Nature 583, 215–220 (2020).
Liu, X. et al. Tunable spin-polarized correlated states in twisted double bilayer graphene. Nature 583, 221–225 (2020).
Polshyn, H. et al. Electrical switching of magnetic order in an orbital Chern insulator. Nature 588, 66–70 (2020).
Shi, Y. et al. Tunable Van Hove singularities and correlated states in twisted trilayer graphene. Preprint at https://arxiv.org/abs/2004.12414 (2020).
Chen, S. et al. Electrically tunable correlated and topological states in twisted monolayer–bilayer graphene. Nat. Phys. https://doi.org/10.1038/s41567-020-01062-6 (2020).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Tang, Y. et al. Simulation of Hubbard model physics in WSe2/WS2 moiré superlattices. Nature 579, 353–358 (2020).
Wang, L. et al. Correlated electronic phases in twisted bilayer transition metal dichalcogenides. Nat. Mater. 19, 861–866 (2020).
Khalaf, E., Kruchkov, A. J., Tarnopolsky, G. & Vishwanath, A. Magic angle hierarchy in twisted graphene multilayers. Phys. Rev. B 100, 085109 (2019).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Chen, G. et al. Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice. Nature 579, 56–61 (2020); correction 581, E3 (2020).
Chen, G. et al. Signatures of tunable superconductivity in a trilayer graphene moiré superlattice. Nature 572, 215–219 (2019).
Tsai, K.-T. et al. Correlated insulating states and transport signature of superconductivity in twisted trilayer graphene moiré of moiré superlattices. Preprint at https://arxiv.org/abs/1912.03375 (2019).
Mora, C., Regnault, N. & Bernevig, B. A. Flatbands and perfect metal in trilayer moiré graphene. Phys. Rev. Lett. 123, 026402 (2019).
Carr, S. et al. Ultraheavy and ultrarelativistic Dirac quasiparticles in sandwiched graphenes. Nano Lett. 20, 3030–3038 (2020).
Lei, C., Linhart, L., Qin, W., Libisch, F. & MacDonald, A. H. Mirror-symmetry breaking and stacking-shift dependence in twisted trilayer graphene. Preprint at https://arxiv.org/abs/2010.05787 (2020).
Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Flavour Hund’s coupling, correlated Chern gaps, and diffusivity in moiré flat bands. Preprint at https://arxiv.org/abs/2008.12296 (2020).
Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Halperin, B. I. & Nelson, D. R. Resistive transition in superconducting films. J. Low Temp. Phys. 36, 599–616 (1979).
He, M. et al. Symmetry breaking in twisted double bilayer graphene. Nat. Phys. 17, 26–30, (2021).
Nandkishore, R., Levitov, L. S. & Chubukov, A. V. Chiral superconductivity from repulsive interactions in doped graphene. Nat. Phys. 8, 158–163 (2012).
Dessau, D. S. et al. Key features in the measured band structure of Bi2Sr2CaCu2O8+δ: flat bands at EF and Fermi surface nesting. Phys. Rev. Lett. 71, 2781–2784 (1993).
Yokoya, T. et al. Extended Van Hove singularity in a noncuprate layered superconductor Sr2RuO4. Phys. Rev. Lett. 76, 3009–3012 (1996).
Nelson, D. R. & Kosterlitz, J. M. Universal jump in the superfluid density of two-dimensional superfluids. Phys. Rev. Lett. 39, 1201–1205 (1977).
Hazra, T., Verma, N. & Randeria, M. Bounds on the superconducting transition temperature: applications to twisted bilayer graphene and cold atoms. Phys. Rev. X 9, 031049 (2019).
Nakagawa, Y. et al. Gate-controlled low carrier density superconductors: toward the two-dimensional BCS–BEC crossover. Phys. Rev. B 98, 064512 (2018).
Wang, Z., Liu, C., Liu, Y. & Wang, J. High-temperature superconductivity in one-unit-cell FeSe films. J. Phys. Condens. Matter 29, 153001 (2017).
Xie, M. & MacDonald, A. H. Weak-field Hall resistivity and spin/valley flavor symmetry breaking in MAtBG. Preprint at https://arxiv.org/abs/2010.07928 (2020).
Khalaf, E., Chatterjee, S., Bultinck, N., Zaletel, M. P. & Vishwanath, A. Charged skyrmions and topological origin of superconductivity in magic-angle graphene. Preprint at https://arxiv.org/abs/2004.00638 (2020).
Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Continuum model of the twisted graphene bilayer. Phys. Rev. B 86, 155449 (2012).
Lopez-Bezanilla, A. & Lado, J. L. Electrical band flattening, valley flux, and superconductivity in twisted trilayer graphene. Phys. Rev. Res. 2, 033357 (2020).
Carr, S., Fang, S., Zhu, Z. & Kaxiras, E. An exact continuum model for low-energy electronic states of twisted bilayer graphene. Phys. Rev. Res. 1, 013001 (2019).
Bistritzer, R. & MacDonald, A. H. Moiré butterflies in twisted bilayer graphene. Phys. Rev. B 84, 035440 (2011).
Zhang, Y.-H., Po, H. C. & Senthil, T. Landau level degeneracy in twisted bilayer graphene: role of symmetry breaking. Phys. Rev. B 100, 125104 (2019).
Tomarken, S. L. et al. Electronic compressibility of magic-angle graphene superlattices. Phys. Rev. Lett. 123, 046601 (2019).
Shoenberg, D. Magnetic Oscillations in Metals (Cambridge Univ. Press, 1984).
Giamarchi, T. & Bhattacharya, S. in High Magnetic Fields: Applications in Condensed Matter Physics and Spectroscopy (eds Berthier, C. et al.) 314–360 (2001).
Acknowledgements
We thank S. Todadri, A. Vishwanath, S. Kivelson, M. Randeria, S. Ilani, L. Fu and A. Georges for discussions. This work has been primarily supported by the US Department of Energy (DOE), Office of Basic Energy Sciences (BES), Division of Materials Sciences and Engineering under award DE-SC0001819 (J.M.P.). Help with transport measurements and data analysis were supported by the National Science Foundation (DMR-1809802), and the STC Center for Integrated Quantum Materials (NSF grant number DMR-1231319; Y.C.). P.J.-H. acknowledges support from the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF9643. P.J.-H. acknowledges partial support by the Fundación Ramon Areces. The development of new nanofabrication and characterization techniques enabling this work has been supported by the US DOE Office of Science, BES, under award DE‐SC0019300. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, grant number JPMXP0112101001, JSPS KAKENHI grant numbers JP20H00354 and the CREST (JPMJCR15F3), JST. This work made use of the Materials Research Science and Engineering Center Shared Experimental Facilities supported by the National Science Foundation (DMR-0819762) and of Harvard’s Center for Nanoscale Systems, supported by the NSF (ECS-0335765).
Author information
Authors and Affiliations
Contributions
J.M.P. and Y.C. fabricated the samples, and performed transport measurements and numerical simulations. K.W. and T.T. provided hBN samples. J.M.P., Y.C., and P.J-H. performed data analysis, discussed the results, and wrote the manuscript with input from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Mathias Scheurer, Ke Wang and Guangyu Zhang for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Stacking order in MATTG.
a, b, Illustrations of A-tw-A stacking (a) and A-tw-B stacking (b), where ‘tw’ denotes the middle twisted layer (L2, orange) and A/B represents the relative stacking order between the topmost (L3, green) and bottommost (L1, blue) layers. c–f, Continuum-model bandstructures of A-tw-A stacked (c, d) and A-tw-B stacked (e, f) MATTG at zero (c, e) and finite (d, f) displacement fields. The twist angle is θ = 1.57° for all plots. g–j, Calculated Landau level sequence corresponding to the bands in c–f. The size of the dots represents the size of the Landau level gaps in the Hofstadter spectrum. For A-tw-A stacking, the major sequence of filling factors near the charge neutrality is ±2, ±6, ±10, …, regardless of the displacement field, whereas for A-tw-B stacking the Landau levels evolve into a symmetry-broken sequence that has 0, ±8 as the dominant filling factors with largest gaps in a finite displacement field. An anisotropy term of β = −0.01 is included in all of the above calculations (see Methods). k, l, Experimentally measured Landau levels in MATTG near the charge neutrality. We find the strongest sequence of ±2, ±6, ±10, … at both D = 0 and D/ε0 = 0.77 V nm−1, consistent with the A-tw-A stacking scenario.
Extended Data Fig. 2 Device schematics and device optical picture.
a, Our device consists of hBN-encapsulated MATTG etched into a Hall bar, Cr/Au contacts on the edge, and top/bottom metallic gates. For transport measurements, we measure current I, longitudinal voltage Vxx, and transverse voltage Vxy, while tuning the density ν and displacement field D by applying top gate voltage Vtg and bottom gate voltage Vbg. b, Optical picture of devices A and B. Device C is lithographically similar.
Extended Data Fig. 3 Robust superconductivity in other MATTG devices (devices B and C).
a, Rxx–T curve. b, Vxx–I and dVxx/dI–I curves. c, I–B map in device B with a smaller-than-magic-angle θ ≈ 1.44°. In this device, maximum TBKT ≈ 0.73 K. The choice of ν is to display the Fraunhofer-like Josephson interference, which demonstrates the superconducting phase coherence. d–f, As in a–c, for device C, with a twist angle θ ≈ 1.4°. Device C has a maximum TBKT of ~0.68 K. f shows a regular B-suppression of Ic with B. Both devices show sharp peaks in dVxx/dI at their critical currents.
Extended Data Fig. 4 Vxx–I curves and critical current Ic in MATTG.
a, Forward (red) and backward (blue) sweeps of Vxx–I curves for the optimal point ν = −2.4 and D/ε0 = −0.44 V nm−1. Inset, A clear hysteresis loop exists in the curve at I ≈ 550–600 nA. b, Map of Ic versus ν and D in the major superconducting regions. c, Evolution of Ic over D at ν = −2.4, showing that Ic initially increases as finite D is applied, and quickly decreases beyond local maxima near |D|/ε0 ≈ 0.48 V nm−1. d, Ic versus D at ν = +2.26 shows that the maximum Ic occurs near |D|/ε0 ≈ 0.71 V nm−1, after which Ic quickly decreases. The modulation of superconducting strength in D may be due to change in the band flatness, as well as the interactions with the electrons in the Dirac bands. e–g, Vxx–I and dVxx/dI–I curves for certain points in superconducting domes near ν = −2 + δ (e), ν = +2 – δ (f), and ν = +2 + δ (g), all showing sharp peaks in dVxx/dI at the critical current.
Extended Data Fig. 5 Rxx versus ν at T = 70 mK, 5 K and 10 K.
a–d, Measured at D/ε0 = 0.77 V nm−1 (a), D/ε0 = 0.52 V nm−1 (b), D/ε0 = 0.26 V nm−1 (c) and D/ε0 = 0 V nm−1 (d).
Extended Data Fig. 6 Hall density analysis.
a–c, Linecuts of Rxx, Rxy and νH (right axis) versus ν at representative D from high to zero, showing the bounding of major superconducting phases within the Hall density features. Vertical red, yellow, and dark blue bars denote ‘gap/Dirac’, ‘reset’ and ‘VHS’ features, respectively, and the light-blue regions denote superconductivity. Purple dashed lines show the expected Hall density. We note that there are some small regions right before ν = +1 and ν = +2 where for certain D values there are signatures of a more complex behaviour in νH, with VHSs possibly very close to the ‘resets’, as shown in Fig. 2b. d, The Hall density νH extracted from smaller magnetic fields of B ≈ 0.1–0.3 T reveals a VHS boundary close to the weak superconducting phase boundary near ν = −2 + δ, which is absent in the Hall density shown in a–c and Fig. 2b extracted from a higher magnetic field of B ≈ −1.5 T to 1.5 T. e, Rxx in the same region as shown in d, where the superconducting boundary is close to the VHSs. All measurements are performed at the base temperature T ≈ 70 mK. SC, superconducting.
Extended Data Fig. 7 Quantum oscillations and effective-mass analysis.
All data shown here are measured at D/ε0 = −0.44 V nm−1. a, b, Quantum oscillations at ν = −2.86 (a) and ν = −2.5 (b) at different T. Grey dashed lines show the peaks used for analysis. Inset, Fit to the Lifshitz–Kosevich formula for the extraction of the effective mass, yielding m*/me = 1.25 ± 0.13 (a) and m*/me = 0.95 ± 0.03 (b). c, d, Quantum oscillations sampled at coarser points in T for the same ν as in a, b. Extracted effective-mass values with these coarser data are m*/me = 1.2 ± 0.2 (c) and m*/me = 0.96 ± 0.09 (d), matching the values from a, b within the uncertainty. e, Quantum oscillations at ν = −2.4 (optimal doping). f, Lifshitz–Kosevich fits for the data shown in c–e, showing δR normalized with its value at the lowest temperature. The peaks chosen for extraction are marked with triangles in c–e. Amp., amplitude; a.u., arbitrary units.
Extended Data Fig. 8 Analysis of the Ginzburg-Landau coherence length.
a, b, Superconducting transitions at perpendicular magnetic fields from B = 0 T to B = 0.2 T (40 mT between curves) for ν = −2 − δ (ν = −2.4; a) and ν = −2 + δ (ν = −1.84; b), from which the Ginzburg–Landau coherence length ξGL is extracted. D/ε0 = −0.44 V nm−1 for both plots. Inset shows \({T}_{{\rm{c}}}^{50 \% }\), \({T}_{{\rm{c}}}^{40 \% }\) and \({T}_{{\rm{c}}}^{30 \% }\) as a function of B, from which we extracted the coherence length ξGL as 9.4 nm, 12.4 nm and 16.1 nm, respectively, for ν = −2 − δ. For ν = −2 + δ, we obtained 38.0 nm, 39.1 nm and 37.1 nm, respectively. We note that for ν = −2 − δ, the Rxx–T curves develop an extra transition (‘knee’) below Tc at finite B, which is possibly related to the melting transition between a vortex solid and a vortex liquid48.
Extended Data Fig. 9 Landau fans for intermediate D.
a, b, Landau fans on the hole-doped (a) and electron-doped sides (b). They show the evolution between small D and large D, which exhibits a hybridization of the features. In a, the Landau fan diagram at D/ε0 = −0.34 V nm−1 for the hole-doped side shows the fans emanating from all integer fillings. An inward-facing fan from ν = −4 starts developing, which meets the outward-facing fan from ν = −3. Note also the appearance of an inward-facing fan from ν = −2, which meets the outward-facing fan from ν = −1. These observations agree with the formation of VHSs around these two regions in the intermediate |D|, where the electron-like carriers become hole-like, as illustrated in Fig. 4d, and identified in Fig. 2b. A small region of superconductivity starts appearing at ν = −2 + δ while the carriers from ν = −2 are present, as shown in Fig. 2a. In b, the Landau fan diagram at D/ε0 = −0.52 V nm−1 on the electron-doped side shows similar VHSs between ν ≈ +1–2 and ν ≈ +3–4. Similar to the hole-doped side, an inward-facing fan from ν = +2 develops and meets with the outward-facing fan from ν = +1. The density range of the inward-facing fan encompasses the appearance of a superconducting region at ν = −2 + δ at this D.
Rights and permissions
About this article
Cite this article
Park, J.M., Cao, Y., Watanabe, K. et al. Tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene. Nature 590, 249–255 (2021). https://doi.org/10.1038/s41586-021-03192-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03192-0
This article is cited by
-
Electric field tunable bandgap in twisted double trilayer graphene
npj 2D Materials and Applications (2024)
-
Twisted-layer boron nitride ceramic with high deformability and strength
Nature (2024)
-
Local gate control of Mott metal-insulator transition in a 2D metal-organic framework
Nature Communications (2024)
-
The discovery of three-dimensional Van Hove singularity
Nature Communications (2024)
-
Local atomic stacking and symmetry in twisted graphene trilayers
Nature Materials (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.