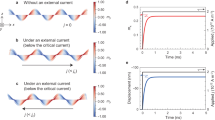
Abstract
An inductor, one of the most fundamental circuit elements in modern electronic devices, generates a voltage proportional to the time derivative of the input current1. Conventional inductors typically consist of a helical coil and induce a voltage as a counteraction to time-varying magnetic flux penetrating the coil, following Faraday’s law of electromagnetic induction. The magnitude of this conventional inductance is proportional to the volume of the inductor’s coil, which hinders the miniaturization of inductors2. Here, we demonstrate an inductance of quantum-mechanical origin3, generated by the emergent electric field induced by current-driven dynamics of spin helices in a magnet. In microscale rectangular magnetic devices with nanoscale spin helices, we observe a typical inductance as large as −400 nanohenry, comparable in magnitude to that of a commercial inductor, but in a volume about a million times smaller. The observed inductance is enhanced by nonlinearity in current and shows non-monotonous frequency dependence, both of which result from the current-driven dynamics of the spin-helix structures. The magnitude of the inductance rapidly increases with decreasing device cross-section, in contrast to conventional inductors. Our findings may pave the way to microscale, simple-shaped inductors based on emergent electromagnetism related to the quantum-mechanical Berry phase.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Change history
02 November 2020
This Article was amended to correct the Peer review information, which was originally incorrect.
References
Landau, L. D. & Lifshitz, E. M. Electrodynamics of Continuous Media Ch. 32 (Pergamon, 1960).
Kang, J. et al. On-chip intercalated-graphene inductors for next-generation radio frequency electronics. Nat. Electron. 1, 46–51 (2018).
Nagaosa, N. Emergent inductor by spiral magnets. Jpn J. Appl. Phys. 58, 120909 (2019).
Meservey, R. & Tedrow, P. M. Measurements of the kinetic inductance of superconducting linear structures. J. Appl. Phys. 40, 2028 (1969).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Yu, X. Z. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Neubauer, A. et al. Topological Hall effect in the A phase of MnSi. Phys. Rev. Lett. 102, 186602 (2009).
Volovik, G. E. Linear momentum in ferromagnets. J. Phys. C 20, L83 (1987).
Froelich, J. & Studer, U. M. Gauge invariance and current algebra in nonrelativistic many-body theory. Rev. Mod. Phys. 65, 733–802 (1993).
Barnes, S. E. & Maekawa, S. Generalization of Faraday’s law to include nonconservative spin forces. Phys. Rev. Lett. 98, 246601 (2007).
Yang, S. A. et al. Universal electromotive force induced by domain wall motion. Phys. Rev. Lett. 102, 067201 (2009).
Hayashi, M. et al. Time-domain observation of the spinmotive force in permalloy nanowires. Phys. Rev. Lett. 108, 147202 (2012).
Yamane, Y. et al. Continuous generation of spinmotive force in a patterned ferromagnetic film. Phys. Rev. Lett. 107, 236602 (2011).
Yamane, Y., Ieda, J. & Sinova, J. Electric voltage generation by antiferromagnetic dynamics. Phys. Rev. B 93, 180408 (2016).
Tatara, G. & Kohno, H. Theory of current-driven domain wall motion: spin transfer versus momentum transfer. Phys. Rev. Lett. 92, 086601 (2004).
Gladyshevskii, R. E., Strusievicz, O. R., Cenzual, K. & Parthé, E. Structure of Gd3Ru4Al12, a new member of the EuMg5.2 structure family with minority atom clusters. Acta Crystallogr. B 49, 474–478 (1993).
Niermann, J. & Jeitschko, W. Ternary rare earth (R) transition metal aluminides R 3T 4Al12 (T = Ru and Os) with Gd3Ru4Al12 type structure. Z. Inorg. Gen. Chem. 628, 2549 (2002).
Nakamura, S. et al. Spin trimer formation in the metallic compound Gd3Ru4Al12 with a distorted kagome lattice structure. Phys. Rev. B 98, 054410 (2018).
Chandragiri, V., Iyer, K. K. & Sampathkumaran, E. V. Magnetic behavior of Gd3Ru4Al12, a layered compound with distorted kagomé net. J. Phys. Condens. Matter 28, 286002 (2016).
Hirschberger, M. et al. Skyrmion phase and competing magnetic orders on a breathing kagomé lattice. Nat. Commun. 10, 5831 (2019).
Iwasaki, J., Mochizuki, M. & Nagaosa, N. Universal current–velocity relation of skyrmion motion in chiral magnets. Nat. Commun. 4, 1463 (2013).
Kleemann, W. Universal domain wall dynamics in disordered ferroic materials. Annu. Rev. Mater. Res. 37, 415 (2007).
Schulz, T. et al. Emergent electrodynamics of skyrmions in a chiral magnet. Nat. Phys. 8, 301–304 (2012).
Yokouchi, T. et al. Current-induced dynamics of skyrmion strings. Sci. Adv. 4, eaat1115 (2018).
Funato, H., Kawamura, A. & Kamiyama, K. Realization of negative inductance using variable active–passive reactance (VAPAR). IEEE Trans. Power Electron. 12, 589 (1997).
Zhang, S. L. et al. Room-temperature helimagnetism in FeGe thin films. Sci. Rep. 7, 123 (2017).
Emori, S., Bauer, U., Ahn, S.-M., Martinez, E. & Beach, G. S. D. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 12, 611–616 (2013).
Yokouchi, T. et al. Formation of in-plane skyrmions in epitaxial MnSi thin films as revealed by planar Hall effect. J. Phys. Soc. Jpn 84, 104708 (2015).
World’s highest inductance values! Expanded lineup of ultra-compact 0201-inch (0603mm)-size high-frequency chip inductors for smartphones — the LQP03TN_02 series-. muRata https://article.murata.com/en-eu/article/expanded-lineup-of-ultra-compact-0201-inch-0603mm-size?intcid5 (2014).
Acknowledgements
We thank M. Kawasaki for discussions. This work was supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (grant no. 19K14667) and Core Research for Evolutional Science and Technology (CREST), Japan Science and Technology Agency (grant no. JPMJCR1874). M.H. was supported as a Humboldt/JSPS International Research Fellow (18F18804).
Author information
Authors and Affiliations
Contributions
Y.T., N.N. and Y.O. conceived the project. T.Y. fabricated the thin-plate devices and conducted transport measurements with assistance from F.K. M.H. grew and characterized the single crystals. T.Y. and N.N. carried out the theoretical analysis. T.Y., Y.T. and N.N. wrote the draft. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Seonghoon Woo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Temperature dependence of longitudinal resistivity.
a, Temperature dependence of resistivity ρxx for the thin-plate sample of Gd3Ru4Al12. b, Magnified image of ρxx–T curve around the transition temperature. The transition temperatures (TN1 and TN2) are denoted by inverse triangles.
Extended Data Fig. 2 Magneto-transport properties with H // c-axis.
a–d, Magnetoresistivity for a thin-plate sample of Gd3Ru4Al12 at various temperatures. We determined the TC phase from the dip structure represented by the blue shading. e–h, Magnetic-field derivative of the magnetoresistivity at various temperatures. We ascribe the kinks to the fan-to-ferromagnetic transition (green triangles) and the phase boundaries of the V phase (light blue triangles). The kinks are also observed at the phase boundaries of the skyrmion phase (red squares). i–l, Magnetic-field dependence of Hall conductivity (σxy) at various temperatures. The red-shaded regions represent the contribution of the topological Hall effect due to the formation of skyrmions.
Extended Data Fig. 3 Frequency dependence of the complex impedance.
Frequency dependence of the imaginary part of the background-subtracted complex impedance (Im ΔZ1f), measured with the lock-in amplifier.
Extended Data Fig. 4 Emergent inductance for various devices with different size and electrode materials.
a–f, Scanning electron microscope images for devices with different sizes and electrode materials. The electrode material is tungsten, except for device 4 in which it is gold. g–k, Magnetic-field dependence of the imaginary part of the background-subtracted impedance (Im ΔZ1f) in thin-plate devices with W electrodes. The green, pink, blue and light blue shading represents H, Sk, TC and fan phases, respectively. l, Magnetic-field dependence of the imaginary part of the complex impedance Im ΔZ1f in a thin-plate device with gold electrodes. m, The magnitude of Im ΔZ1f as a function of the distance of the voltage electrodes (delectrode). The definition of delectrode is shown in the inset. Here, the cross-sectional area is the same for all devices shown in m.
Extended Data Fig. 5 Magneto-transport properties with H parallel to the a-axis.
a, Magnetoresistivity measured with magnetic field (H) and current (I) parallel to the a-axis at 5.5 K. b, c, Magnetic-field dependence of planar Hall resistivity (\({\rho }_{yx}^{{\rm{PHE}}}\)) at 0.4 T (b) and 1.5 T (c). The experimental set-up is shown in the inset in b. The red line in c is a fit to sin 2θH.
Extended Data Fig. 6 Emergent inductance measured with LCR meter.
a, Frequency dependence of complex impedance Z from which we calculated the complex inductance \(\mathop{L}\limits^{ \sim }(\omega )={L}^{{\prime} }(\omega )+i{L}^{{\prime\prime} }(\omega )\) (Fig. 4b). The inset is the magnified view of Im Z in the low-frequency range on a linear scale. Grey shading corresponds to the grey-shaded region in Fig. 4b. b, Frequency dependence of \(\tilde{L}(\omega )\) for a thin-plate device with gold electrodes. c–e, Magnetic field dependence of the imaginary part of the complex impedance (Im Z) measured with an LCR meter at various temperatures, for magnetic field applied in the hexagonal plane. See Methods for the procedure for extracting the bulk contribution of Z.
Supplementary information
Supplementary Information
This Supplementary Information file contains the following sections: Current-induced dynamics of helix; Derivation of emergent inductance; The sign of emergent inductance; and Frequency dependence of the current-induced dynamics of a helix.
Rights and permissions
About this article
Cite this article
Yokouchi, T., Kagawa, F., Hirschberger, M. et al. Emergent electromagnetic induction in a helical-spin magnet. Nature 586, 232–236 (2020). https://doi.org/10.1038/s41586-020-2775-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2775-x
This article is cited by
-
Energetic perspective on emergent inductance exhibited by magnetic textures in the pinned regime
npj Spintronics (2023)
-
Symmetry of the emergent inductance tensor exhibited by magnetic textures
npj Spintronics (2023)
-
Evidence of non-collinear spin texture in magnetic moiré superlattices
Nature Physics (2023)
-
Electromagnetic response in spiral magnets and emergent inductance
Communications Physics (2021)
-
Inductors enter the world of quantum mechanics
Nature (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.