Abstract
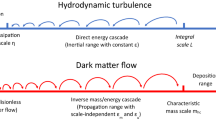
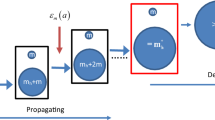
Cosmological models in which dark matter consists of cold elementary particles predict that the dark halo population should extend to masses many orders of magnitude below those at which galaxies can form1,2,3. Here we report a cosmological simulation of the formation of present-day haloes over the full range of observed halo masses (20 orders of magnitude) when dark matter is assumed to be in the form of weakly interacting massive particles of mass approximately 100 gigaelectronvolts. The simulation has a full dynamic range of 30 orders of magnitude in mass and resolves the internal structure of hundreds of Earth-mass haloes in as much detail as it does for hundreds of rich galaxy clusters. We find that halo density profiles are universal over the entire mass range and are well described by simple two-parameter fitting formulae4,5. Halo mass and concentration are tightly related in a way that depends on cosmology and on the nature of the dark matter. For a fixed mass, the concentration is independent of the local environment for haloes less massive than those of typical galaxies. Haloes over the mass range of 10−3 to 1011 solar masses contribute about equally (per logarithmic interval) to the luminosity produced by dark matter annihilation, which we find to be smaller than all previous estimates by factors ranging up to one thousand3.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data generated, analysed and presented in this study are available from the corresponding authors on request, although the requester will be responsible for providing the very considerable resources needed for transferring and storing these data.
Code availability
The parent code GADGET-2 has been publicly available for some time. It is expected that most of the extensions and modifications made to meet the extreme requirements of this project will be made available in the future release of GADGET-4; those interested can contact V.S. (vspringel@MPA-Garching.mpg.de) for further information. The very large white-noise field, Panphasia, used to code our initial conditions, is also publicly available; those interested can contact A.J. (A.R.Jenkins@durham.ac.uk).
References
Blumenthal, G. R., Faber, S. M., Primack, J. R. & Rees, M. J. Formation of galaxies and large-scale structure with cold dark matter. Nature 311, 517–525 (1984).
White, S. D. M. & Frenk, C. S. Galaxy formation through hierarchical clustering. Astrophys. J. 379, 52–79 (1991).
Bertone, G., Hooper, D. & Silk, J. Particle dark matter: evidence, candidates and constraints. Phys. Rep. 405, 279–390 (2005).
Navarro, J. F., Frenk, C. S. & White, S. D. M. A universal density profile from hierarchical clustering. Astrophys. J. 490, 493–508 (1997).
Navarro, J. F. et al. The inner structure of Λ CDM haloes—III. Universality and asymptotic slopes. Mon. Not. R. Astron. Soc. 349, 1039–1051 (2004).
Springel, V. et al. Simulations of the formation, evolution and clustering of galaxies and quasars. Nature 435, 629–636 (2005).
Navarro, J. F., Frenk, C. S. & White, S. D. M. The structure of cold dark matter halos. Astrophys. J. 462, 563 (1996).
Einasto, J. On the construction of a composite model for the galaxy and on the determination of the system of galactic parameters. Trudy Astrofizicheskogo Instituta Alma-Ata 5, 87–100 (1965).
Ludlow, A. D. et al. The mass–concentration–redshift relation of cold dark matter haloes. Mon. Not. R. Astron. Soc. 441, 378–388 (2014).
Ludlow, A. D. et al. The mass–concentration–redshift relation of cold and warm dark matter haloes. Mon. Not. R. Astron. Soc. 460, 1214–1232 (2016).
Springel, V. et al. The Aquarius project: the subhaloes of galactic haloes. Mon. Not. R. Astron. Soc. 391, 1685–1711 (2008).
Stücker, J., Busch, P. & White, S. D. M. The median density of the Universe. Mon. Not. R. Astron. Soc. 477, 3230–3246 (2018).
Diemand, J., Moore, B. & Stadel, J. Earth-mass dark-matter haloes as the first structures in the early Universe. Nature 433, 389–391 (2005).
Ishiyama, T., Makino, J. & Ebisuzaki, T. Gamma-ray signal from earth-mass dark matter microhalos. Astrophys. J. Lett. 723, L195–L200 (2010).
Anderhalden, D. & Diemand, J. Density profiles of CDM microhalos and their implications for annihilation boost factors. J. Cosmol. Astropart. Phys. 04, 009 (2013).
Angulo, R. E., Hahn, O., Ludlow, A. D. & Bonoli, S. Earth-mass haloes and the emergence of NFW density profiles. Mon. Not. R. Astron. Soc. 471, 4687–4701 (2017).
Tseliakhovich, D. & Hirata, C. Relative velocity of dark matter and baryonic fluids and the formation of the first structures. Phys. Rev. D 82, 083520 (2010).
Neto, A. F. et al. The statistics of Λ CDM halo concentrations. Mon. Not. R. Astron. Soc. 381, 1450–1462 (2007).
Sánchez-Conde, M. A. & Prada, F. The flattening of the concentration–mass relation towards low halo masses and its implications for the annihilation signal boost. Mon. Not. R. Astron. Soc. 442, 2271–2277 (2014).
Dutton, A. A. & Macciò, A. V. Cold dark matter haloes in the Planck era: evolution of structural parameters for Einasto and NFW profiles. Mon. Not. R. Astron. Soc. 441, 3359–3374 (2014).
Diemer, B. & Joyce, M. An accurate physical model for halo concentrations. Astrophys. J. 871, 168 (2019).
Ade, P. A. R. et al. (Planck Collaboration) Planck 2013 results. I. Overview of products and scientific results. Astron. Astrophys. 571, A1 (2014).
Schaye, J. et al. The EAGLE project: simulating the evolution and assembly of galaxies and their environments. Mon. Not. R. Astron. Soc. 446, 521–554 (2015).
Lewis, A., Challinor, A. & Lasenby, A. Efficient computation of cosmic microwave background anisotropies in closed Friedmann–Robertson–Walker Models. Astrophys. J. 538, 473–476 (2000).
Bardeen, J. M., Bond, J. R., Kaiser, N. & Szalay, A. S. The statistics of peaks of Gaussian random fields. Astrophys. J. 304, 15 (1986).
Springel, V. et al. Prospects for detecting supersymmetric dark matter in the Galactic halo. Nature 456, 73–76 (2008).
Green, A. M., Hofmann, S. & Schwarz, D. J. The power spectrum of SUSY-CDM on subgalactic scales. Mon. Not. R. Astron. Soc. 353, L23–L27 (2004).
Martinez, G. D. et al. Indirect dark matter detection from dwarf satellites: joint expectations from astrophysics and supersymmetry. J. Cosmol. Astropart. Phys. 06, 014 (2009).
Bertone, G. & Tait, T. M. P. A new era in the search for dark matter. Nature 562, 51–56 (2018).
Jenkins, A. Second-order Lagrangian perturbation theory initial conditions for resimulations. Mon. Not. R. Astron. Soc. 403, 1859–1872 (2010).
Jenkins, A. A new way of setting the phases for cosmological multiscale Gaussian initial conditions. Mon. Not. R. Astron. Soc. 434, 2094–2120 (2013).
Jenkins, A. & Booth, S. Panphasia: a user guide. Preprint at https://arXiv.org/abs/1306.5771 (2013).
Springel, V. The cosmological simulation code GADGET-2. Mon. Not. R. Astron. Soc. 364, 1105–1134 (2005).
Barnes, J. & Hut, P. A hierarchical O(N log N) force-calculation algorithm. Nature 324, 446–449 (1986).
Dehnen, W. A very fast and momentum-conserving tree code. Astrophys. J. Lett. 536, L39–L42 (2000).
Pelupessy, F. I., Jänes, J. & Portegies Zwart, S. N-body integrators with individual time steps from hierarchical splitting. New Astron. 17, 711–719 (2012).
Wang, J. & White, S. D. M. Discreteness effects in simulations of hot/warm dark matter. Mon. Not. R. Astron. Soc. 380, 93–103 (2007).
Power, C. et al. The inner structure of ΛCDM haloes—I. A numerical convergence study. Mon. Not. R. Astron. Soc. 338, 14–34 (2003).
Gao, L. et al. The redshift dependence of the structure of massive Λ cold dark matter haloes. Mon. Not. R. Astron. Soc. 387, 536–544 (2008).
Lavalle, J., Yuan, Q., Maurin, D. & Bi, X. J. Full calculation of clumpiness boost factors for antimatter cosmic rays in the light of Λ CDM N-body simulation results. Abandoning hope in clumpiness enhancement? Astron. Astrophys. 479, 427–452 (2008).
Sheth, R. K. & Tormen, G. An excursion set model of hierarchical clustering: ellipsoidal collapse and the moving barrier. Mon. Not. R. Astron. Soc. 329, 61–75 (2002).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (NSFC) under grant 11988101, the National Key Program for Science and Technology Research Development (2017YFB0203300), and the UK Science and Technology Facilities Council (STFC) consolidated grant ST/P000541/1 to Durham University. J.W. and L.G. acknowledge support by NSFC grants 11373029, 11873051 and 11851301. S.B. acknowledges support from Harvard University through the ITC Fellowship. C.S.F. acknowledges support by the European Research Council (ERC) through Advanced Investigator grant DMIDAS (GA 786910). The visualizations in Fig. 1 were produced with the py-sphviewer code (http://github.com/alejandrobll/py-sphviewer). This work used the DiRAC@Durham facility managed by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (http://www.dirac.ac.uk). The equipment was funded by BEIS capital funding via STFC capital grants ST/K00042X/1, ST/P002293/1 and ST/R002371/1, Durham University and STFC operations grant ST/R000832/1. DiRAC is part of the National e-Infrastructure.
Author information
Authors and Affiliations
Contributions
J.W. contributed to the design of the project, carried out simulations, performed analysis and wrote the first draft of the paper. S.B. contributed to design of project, carried out simulations and performed analysis. C.S.F. contributed to the concept of project and its design, analysis of results and writing of final draft. A.J. contributed to the design of the project, upgraded initial conditions code and generated initial conditions, and contributed to analysis of results. L.G. contributed to the design of the project and analysis of results. V.S. wrote and upgraded simulation code, carried out simulations and contributed to analysis of results. S.D.M.W. initially conceived the project, and contributed to its design, analysis of results and writing of final draft.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Mike Boylan-Kolchin and James Bullock for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Projected density maps for different zoom levels.
a–f, Levels L1, L3 and L8c (a, c, e) are compared with maps of the same regions in their parent levels L0, L2 and L7c respectively (b, d, f). The regions shown are the largest spheres that fit almost entirely within the high-resolution region of the higher level. Only high-resolution particles are used to make the images.
Extended Data Fig. 2 The cumulative halo number as a function of mass, M200, in the high-resolution region of each zoom level compared with that in the same region of the parent level.
Different colours denote different levels as indicated in the legend. Results from the parent levels are shown as dotted curves. The two vertical black dotted lines indicate the upper mass limit for spurious haloes in L7c and L8c, calculated as described in ref. 37. Note the excellent agreement between the solid and dotted curves above the resolution limit of the latter (and above the L7c mass limit for spurious haloes in the case of L7c versus L8c).
Extended Data Fig. 3 Comparison of the density profile of a massive halo at each level with that of its counterpart in the parent level.
a, The density profile of one of the most massive haloes in the high-resolution region of each zoom level is compared with that of the same halo at the parent level. Results from different levels are shown with different colours, as indicated by the legend, which also gives the masses of the haloes concerned. Higher-resolution profiles are shown as dashed curves, while those from the parent levels are shown as solid curves. The range between the convergence radius and r200 is plotted as a thick line in the lower-resolution case. b, The ratio of the density profiles of each pair in the upper panel. Again, results in the range between the convergence radius in the lower-resolution case and r200 are shown as thick lines. Note the excellent convergence between simulation pairs over this radial range, which typically differ in mass resolution by a factor of several hundred.
Extended Data Fig. 4 Dependence of halo concentration on local environment in the high-resolution region at each zoom level.
Results are shown for haloes in the mass range [0.5, 2]Mchar; the key gives the characteristic mass, Mchar, for each level and also defines the colour key. Each white curve gives the median concentration for the best-fit Einasto profile, while the surrounding coloured region gives the r.m.s. scatter. Local environment density is defined here as the mean in a thick spherical shell, 5 < r/r200 < 10, surrounding each halo, and is given in units of the critical density. All haloes are used for this plot. A vertical dotted line shows the cosmic mean density. Note that although concentration depends strongly on mass, any dependence on local environment density is weak.
Extended Data Fig. 5 Stacked density profiles of matched haloes in two L7 simulations.
The result for the L7 and the L7c are presented as solid and dashed curves individually. The densities are multiplied by r2 to increase the dynamical range of the figure. Different colours correspond to different mass bins with central values quoted in the legend. The profiles are shown as thick lines over the range where they are most reliable, between the convergence radius, rconv, and r200. The vertical dotted line indicates the softening length in the high-resolution region at this level. The effect of the free-streaming cut-off is to reduce the density in the inner parts, and therefore the concentration, by an increasing amount as the halo mass approaches the free-streaming mass.
Extended Data Fig. 6 The mean luminosity density produced by dark matter annihilation in today’s Universe as a function of halo mass.
Solid coloured lines indicate estimates obtained by multiplying the mean \(\langle L/M\rangle \) obtained from well resolved, simulated haloes by the halo number density predicted for each bin by the Sheth–Tormen halo mass function41. Shaded regions indicate the estimated 1σ uncertainty. Dashed curves indicate results found if we instead use \(\langle L/M\rangle \) values predicted by previously published mass–concentration relations (light blue21, yellow10, red19, green20, dark blue18). Corresponding predictions for the total integrated luminosity density are given in the key by values preceding each model’s name. Note that the units of annihilation luminosity are arbitrary, so only ratios of values are meaningful.
Rights and permissions
About this article
Cite this article
Wang, J., Bose, S., Frenk, C.S. et al. Universal structure of dark matter haloes over a mass range of 20 orders of magnitude. Nature 585, 39–42 (2020). https://doi.org/10.1038/s41586-020-2642-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2642-9
This article is cited by
-
Dynamics of stochastic-constrained particles
Scientific Reports (2023)
-
Large-scale dark matter simulations
Living Reviews in Computational Astrophysics (2022)
-
Kinetic field theory for cosmic structure formation
La Rivista del Nuovo Cimento (2022)
-
Probing small-scale power spectra with pulsar timing arrays
Journal of High Energy Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.