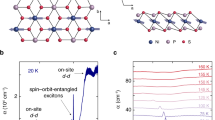
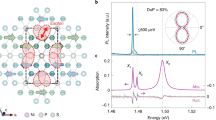
Abstract
An exciton is the bosonic quasiparticle of electron–hole pairs bound by the Coulomb interaction1. Bose–Einstein condensation of this exciton state has long been the subject of speculation in various model systems2,3, and examples have been found more recently in optical lattices and two-dimensional materials4,5,6,7,8,9. Unlike these conventional excitons formed from extended Bloch states4,5,6,7,8,9, excitonic bound states from intrinsically many-body localized states are rare. Here we show that a spin–orbit-entangled exciton state appears below the Néel temperature of 150 kelvin in NiPS3, an antiferromagnetic van der Waals material. It arises intrinsically from the archetypal many-body states of the Zhang–Rice singlet10,11, and reaches a coherent state assisted by the antiferromagnetic order. Using configuration-interaction theory, we determine the origin of the coherent excitonic excitation to be a transition from a Zhang–Rice triplet to a Zhang–Rice singlet. We combine three spectroscopic tools—resonant inelastic X-ray scattering, photoluminescence and optical absorption—to characterize the exciton and to demonstrate an extremely narrow excitonic linewidth below 50 kelvin. The discovery of the spin–orbit-entangled exciton in antiferromagnetic NiPS3 introduces van der Waals magnets as a platform to study coherent many-body excitons.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper, and other findings of this study, are available from the corresponding authors upon reasonable request. Source data are provided with this paper.
References
Frenkel, J. On the transformation of light into heat in solids. I. Phys. Rev. 37, 17–44 (1931).
Lozovik, Yu. E. & Yudson, V. I. Feasibility of superfluidity of paired spatially separated electrons and holes; a new superconductivity mechanism. JETP Lett. 22, 274–276 (1975).
Nandi, D., Finck, A. D. K., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Exciton condensation and perfect Coulomb drag. Nature 488, 481–484 (2012).
Butov, L. V., Gossard, A. C. & Chemla, D. S. Macroscopically ordered state in an exciton system. Nature 418, 751–754 (2002).
Snoke, D., Denev, S., Liu, Y., Pfeiffer, L. & West, K. Long-range transport in excitonic dark states in coupled quantum wells. Nature 418, 754–757 (2002).
Wang, K. et al. Electrical control of charged carriers and excitons in atomically thin materials. Nat. Nanotechnol. 13, 128–132 (2018).
Eisenstein, J. P. Exciton condensation in bilayer quantum Hall systems. Annu. Rev. Condens. Matter Phys. 5, 159–181 (2014).
Eisenstein, J. P. & Macdonald, A. H. Bose–Einstein condensation of excitons in bilayer electron systems. Nature 432, 691–694 (2004).
Unuchek, D. et al. Room-temperature electrical control of exciton flux in a van der Waals heterostructure. Nature 560, 340–344 (2018).
Zhang, F. C. & Rice, T. M. Effective Hamiltonian for the superconducting Cu oxides. Phys. Rev. B 37, 3759(R) (1988).
Khomskii, D. I. Transition Metal Compounds (Cambridge Univ. Press, 2014).
Friemel, G. et al. Resonant magnetic exciton mode in the heavy-fermion antiferromagnet CeB6. Nat. Commun. 3, 830 (2012).
Park, J.-G. Opportunities and challenges of 2D magnetic van der Waals materials: magnetic graphene? J. Phys. Condens. Matter 28, 301001 (2016).
Burch, K. S., Mandrus, D. & Park, J.-G. Magnetism in two-dimensional van der Waals materials. Nature 563, 47–52 (2018).
Brec, R. Review on structural and chemical properties of transition metal phosphorous trisulfides MPS3. Solid State Ion. 22, 3–30 (1986).
Joy, P. A. & Vasudevan, S. Magnetism in the layered transition-metal thiophosphates MPS3 (M = Mn, Fe, and Ni). Phys. Rev. B 46, 5425–5433 (1992).
Wildes, A. R. et al. Magnetic structure of the quasi-two-dimensional antiferromagnet NiPS3. Phys. Rev. B 92, 224408 (2015).
Kuo, C.-T. et al. Exfoliation and Raman spectroscopic fingerprint of few-layer NiPS3 van der Waals crystals. Sci. Rep. 6, 20904 (2016).
Lee, J.-U. et al. Ising-type magnetic ordering in atomically thin FePS3. Nano Lett. 16, 7433–7438 (2016).
Gong, C. et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 546, 265–269 (2017).
Huang, B. et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 546, 270–273 (2017).
Fei, Z. et al. Ferroelectric switching of a two-dimensional metal. Nat. Mater. 560, 336–339 (2018).
Kim, S. Y. et al. Charge-spin correlation in van der Waals antiferromagnet NiPS3. Phys. Rev. Lett. 120, 136402 (2018).
Kim, K. et al. Suppression of magnetic ordering in XXZ-type antiferromagnetic monolayer NiPS3. Nat. Commun. 10, 345 (2019).
Susner, M. A., Chyasnavichyus, M., McGuire, M. A., Ganesh, P. & Maksymovych, P. Metal thio- and selenophosphates as multifunctional van der Waals layered materials. Adv. Mater. 29, 1602852 (2017).
Bernasconi, M. et al. Lattice dynamics of layered MPX. Phys. Rev. B 38, 12089–12099 (1988).
Monney, C. et al. Determining the short-range spin correlations in the spin-chain Li2CuO2 and CuGeO3 compounds using resonant inelastic x-ray scattering. Phys. Rev. Lett. 110, 087403 (2013).
Collart, E. et al. Localized and delocalized excitons: resonant inelastic X-ray scattering in La2– xSrxNiO4 and La2− xSrxCuO4. Phys. Rev. Lett. 96, 157004 (2006).
Vehse, W. E., Lee, K. H., Yun, S. I. & Sibley, W. A. Ni2+ emission in MgO, KMgF3, KZnF3, and MgF2. J. Lumin. 10, 149–162 (1975).
Joy, P. A. & Vasudevan, S. Optical-absorption spectra of the layered transition-metal thiophosphates MPS3 (M = Mn, Fe, and Ni). Phys. Rev. B 46, 5134–5141 (1992).
Kozielski, M., Pollini, I. & Spinolo, G. Electric absorption spectra of Ni2+ in NiCl2 and NiBr2 (phonon and magnon sidebands). J. Phys. C 5, 1253–1264 (1972).
Lane, C. & Zhu, J.-X. Thickness dependence of electronic structure and optical properties of a correlated van der Waals antiferromagnet NiPS3 thin film. Preprint at https://arXiv.org/abs/2003.01614 (2020).
de Groot, F. Multiplet effects in X-ray spectroscopy. Coord. Chem. Rev. 249, 31–63 (2005).
Acknowledgements
We thank F. de Groot, C. Belvin, E. Baldini and N. Gedik for discussions. The CCES was supported by the Institute for Basic Science (IBS) in Korea (grant number IBS-R009-G1). The work at Sogang University and Yonsei University was supported by National Research Foundation (NRF) grants funded by the Korean government (MSIT; grants 2019R1A2C3006189 and 2019R1I1A2A01062306), the SRC programme (vdWMRC; grant number 2017R1A5A1014862) and by a grant (2013M3A6A5073173) from the Center for Advanced Soft Electronics under the Global Frontier Research Program of the Ministry of Science and ICT of Korea. Work at the Korea Institute for Advanced Study (KIAS) was supported by KIAS individual grants (CG031509 and CG068701). We thank the KIAS for providing computing resources (the KIAS Center for Advanced Computation Linux Cluster System) for this work. We acknowledge Diamond Light Source for time on beamline I21 under proposals SP18503 and SP18906. J.-G.P. was partially supported by the Leading Researcher Program of the National Research Foundation of Korea (grant number 2020R1A3B2079375).
Author information
Authors and Affiliations
Contributions
J.-G.P. initiated the project; J.-G.P., J.H.K., H.C. and Y.-W.S. supervised the project. The samples were synthesized and characterized by S.K. and S.L. PL experiments were carried out by K.K., J.-U.L. and H.C. Optical absorption measurements were done by J.K., K.I.S. and J.H.K. The theoretical calculations were made by B.H.K. and Y.-W.S. J.-G.P. and L.C. discussed the RIXS experiments, which were carried out by S.K., S.Y., T.K., A.N., A.W., M.G.-F., J.L., J.-G.P. and K.J.Z. S.K. analysed the RIXS data together with B.H.K. and K.P. J.-G.P., S.K., B.H.K., Y.-W.S., J.H.K. and H.C. wrote the manuscript with comments from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Full crystal structure and single-crystal XRD data from one of the NiPS3 samples.
Left, crystal structure. Thin lines indicate the unit cell, and the Ni lattice (with space group C2/m) is highlighted by the blue bonds. Right, single-crystal XRD data.
Extended Data Fig. 2 PL data taken with different laser energies.
a, Excitation-energy-dependent PL spectra of bulk NiPS3 at T = 10 K. Several peaks below the excitation energy are Raman (phonon and two-magnon) signals. The peaks highlighted by asterisks shift with the excitation energy. b, Excitation-energy dependence of the spectrum near peak I. c, Spectra plotted in terms of energy shift ∆E (∆E = Eexc − Eph, where Eexc is excitation energy and Eph is photon emission energy) for different excitation energies. The peaks highlighted by an asterisk show the same energy shift for all excitation energies. The vertical dashed red line shows that the peak at 0.98 eV is well aligned for all five different energies after correcting for the energy-dependent shift.
Extended Data Fig. 3 Thickness, temperature and polarization dependence of PL in NiPS3.
a, PL spectra as a function of sample thickness (1L indicates monolayer, and so on). b, c, The dependence of peak energy (b) and intensity (c) on sample thickness. d, Temperature-dependent PL spectra of bulk NiPS3. e, Thickness dependence of PL spectra for 1- to 8-layer NiPS3 at 10 K. f, Polarized Raman spectra as a function of sample thickness, measured in the parallel and cross-polarization configurations. The incident polarization was aligned along the a axis of the sample. Scattered photons with polarization along the a (b) axis were measured in the parallel (cross-) polarization configuration. In the bilayer, where antiferromagnetism (AFM) is observed with a lower TN than in the bulk, we interpret the disappearance of peak I as being caused by an unstable AFM ground state, as evidenced by the lower TN. In this connection, in our previous work24, the splitting of the Raman peak at about 180 cm–1 was used as the indicator of AFM ordering. Although the splitting is still visible in the case of the bilayer, the two peaks (red and black) are not as clearly resolved as in the case of thicker crystals, indicating that the AFM ordering is not so robust in the case of thinner samples.
Extended Data Fig. 4 Polarization dependence of peak I in PL spectra, and the effect of magnetic field on optical absorption spectra.
a, Polarization dependence of PL spectra of bulk crystal at T = 10 K, showing peak I and the two high-energy side peaks, Sα and Sβ (respectively left to right). b–d, Intensities of peak I (b), Sα (c) and Sβ (d). 0° is the a axis of NiPS3. e, f, Effect on optical absorption spectra of a magnetic field applied perpendicular to (e) and parallel to (f) the basal plane (measured at 4 K; e shows the field being varied from 0 T to 7 T, and f shows a field of 0 T and a field of 7 T). In the insets, short arrows represent the zig-zag spins of Ni2+, and the circle (e) and the long arrows (f) represent the direction of the field. The intensity variation in f is due to remounting the sample, which leads to some variation of orientation with respect to the fixed direction of the magnetic field. For the perpendicular field configuration (e), remounting of the sample was not necessary.
Extended Data Fig. 5 Theoretical energy diagrams.
a, Splitting of the NiS6 cluster mutiplet with parameters shown in Extended Data Table 1 as a function of hopping strength. Here r is the scale parameter of hopping strengths like Vpdσ = −0.74r eV and Vpdπ = 0.4r eV. Magenta, green, light blue and red lines represent the energy levels of singlet, doublet, triplet and nonuplet states, respectively. Dashed orange and solid grey lines refer to the energy levels of charge-transfer states which are not coupled with d8 multiplets. Because the multiplets shown by grey lines are weakly coupled with d10L2 multiplets, their energy is slightly lower than that of multiplets shown by dashed orange lines. The irreducible representations for r = 0 and r = 1 are given on the top and bottom axes. b, Schematic diagram of the nature of the bonding between d8 and d9L1 multiplets. Dotted red and dashed blue lines represent respectively the pdσ- and pdπ-type bonding between d8 and d9L1 multiplets.
Extended Data Fig. 6 Theoretical and experimental RIXS spectra for various parameters.
Thick dark-violet lines, theoretical results; thin sea-green lines, experimental results. Shown are RIXS spectra at 585.1 eV incident X-ray energy for various parameters as follows: a, charge-transfer energies Δ (left to right, 0.55, 0.95 and 1.35 eV); b, Slater–Condon parameter \({F}_{dd}^{0}\) (4, 6 and 8 eV); c, Slater–Condon parameters \({F}_{dd}^{2}\) and \({F}_{dd}^{4}\) (80%, 100% and 120% of atomic values); d, hopping parameter \({V}_{pd{\rm{\sigma }}}\) (−0.70, −0.74 and −0.78 eV); and e, hopping parameter \({V}_{pd{\rm{\pi }}}\) (0.36, 0.40 and 0.44 eV). Atomic values of \({F}_{dd}^{2}\) and \({F}_{dd}^{4}\) are 12.2341 and 7.5981 eV, respectively. Remaining parameters are set to the values shown in Extended Data Table 1.
Extended Data Fig. 7 Peak-fitting of the RIXS data, the magnon dispersion and the two-magnon continuum in the XXZ-type antiferromagnet NiPS3.
a–e, Two excitonic modes (peaks I and II) are fitted using a Voigt function at several representative temperatures in addition to two charge-transfer peaks (dashed lines). f, Low-energy excitations in the RIXS spectra, showing the Q|| dependence along the b* axis at 14 K. Black squares and red circles correspond to the fitted magnon and two-magnon energies, respectively. The error bars are the standard deviations of the fitting results. g, Calculated magnon spin waves and two-magnon density of states using parameters described in the text: data points and error bars are as in f.
Extended Data Fig. 9 Schematic diagrams of spin configuration and hole density of an S2 ligand in a Ni2S10 cluster.
a, Zhang–Rice triplet (ZRT) lattice; b, two Zhang–Rice singlet (ZRS) excited lattices with the zig-zag AFM order. Large (small) red and blue arrows refer to the spin direction of Ni 3d (S 3p) holes. Green ellipsoids indicate edge-shared S sites, in which spins of two ligand holes are antiparallel with one another. Magenta circles highlight sites of ZRS excitations. Open arrows inside magenta circles represent the direction of anticipated electric dipoles for the ZRS excitation. Owing to polarization reversal with the Ni spin flip, polarized PL along the b direction (the ‘armchair’ direction of the hexagonal Ni network) has destructive contributions from the opposite spin orientations, while the polarized PL along the a direction (the zig-zag direction) has not. This can explain the observed PL anisotropy shown in Extended Data Fig. 4. c–f, Hole density of an S2 ligand as a function of the strength of the long-range magnetic field, h: c, e, for the ground state (GS) with Jp = 0 (c) and Jp = 0.4 eV (e); and d, f, for the excited state near 1.44 eV characterized by the ZRS state with Jp = 0 (d) and Jp = 0.4 eV (f). Other parameters are presented in Extended Data Table 1. In c–f, FM (AFM) indicates that applied long-range magnetic fields at two Ni sites are parallel (antiparallel). We assume the field direction is along the a axis because the result is almost same regardless of the field direction.
Rights and permissions
About this article
Cite this article
Kang, S., Kim, K., Kim, B.H. et al. Coherent many-body exciton in van der Waals antiferromagnet NiPS3. Nature 583, 785–789 (2020). https://doi.org/10.1038/s41586-020-2520-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2520-5
This article is cited by
-
Magnetically propagating Hund’s exciton in van der Waals antiferromagnet NiPS3
Nature Communications (2024)
-
Spin-mediated shear oscillators in a van der Waals antiferromagnet
Nature (2023)
-
A Hubbard exciton fluid in a photo-doped antiferromagnetic Mott insulator
Nature Physics (2023)
-
Composition and phase engineering of metal chalcogenides and phosphorous chalcogenides
Nature Materials (2023)
-
Magnetic proximity boosts chiral quantum emission
Nature Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.