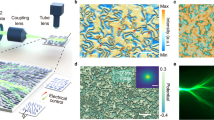
Abstract
When waves propagate through a weak disordered potential with correlation length larger than the wavelength, they form channels (branches) of enhanced intensity that keep dividing as the waves propagate1. This fundamental wave phenomenon is known as branched flow. It was first observed for electrons1,2,3,4,5,6 and for microwave cavities7,8, and it is generally expected for waves with vastly different wavelengths, for example, branched flow has been suggested as a focusing mechanism for ocean waves9,10,11, and was suggested to occur also in sound waves12 and ultrarelativistic electrons in graphene13. Branched flow may act as a trigger for the formation of extreme nonlinear events14,15,16,17 and as a channel through which energy is transmitted in a scattering medium18. Here we present the experimental observation of the branched flow of light. We show that, as light propagates inside a thin soap membrane, smooth thickness variations in the film act as a correlated disordered potential, focusing the light into filaments that display the features of branched flow: scaling of the distance to the first branching point and the probability distribution of the intensity. We find that, counterintuitively, despite the random variations in the medium and the linear nature of the effect, the filaments remain collimated throughout their paths. Bringing branched flow to the field of optics, with its full arsenal of tools, opens the door to the investigation of a plethora of new ideas such as branched flow in nonlinear media, in curved space or in active systems with gain. Furthermore, the labile nature of soap films leads to a regime in which the branched flow of light interacts and affects the underlying disorder through radiation pressure and gradient force.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data are available upon request.
References
Topinka, M. A. et al. Coherent branched flow in a two-dimensional electron gas. Nature 410, 183–186 (2001).
Shaw, S. E. J. Propagation in smooth random potentials. PhD thesis, Harvard (2002); https://search.proquest.com/docview/305536276.
Aidala, K. E. et al. Imaging magnetic focusing of coherent electron waves. Nat. Phys. 3, 464–468 (2007).
Jura, M. P. et al. Unexpected features of branched flow through high-mobility two-dimensional electron gases. Nat. Phys. 3, 841–845 (2007).
Maryenko, D. et al. How branching can change the conductance of ballistic semiconductor devices. Phys. Rev. B 85, 195329 (2012).
Liu, B. & Heller, E. J. Stability of branched flow from a quantum point contact. Phys. Rev. Lett. 111, 236804 (2013).
Höhmann, R., Kuhl, U., Stöckmann, H.-J., Kaplan, L. & Heller, E. J. Freak waves in the linear regime: a microwave study. Phys. Rev. Lett. 104, 093901 (2010).
Barkhofen, S., Metzger, J. J., Fleischmann, R., Kuhl, U. & Stöckmann, H.-J. Experimental observation of a fundamental length scale of waves in random media. Phys. Rev. Lett. 111, 183902 (2013).
Heller, E. J., Kaplan, L. & Dahlen, A. Refraction of a Gaussian seaway. J. Geophys. Res. Oceans 113, https://doi.org/10.1029/2008JC004748 (2008).
Ying, L. H., Zhuang, Z., Heller, E. J. & Kaplan, L. Linear and nonlinear rogue wave statistics in the presence of random currents. Nonlinearity 24, R67 (2011).
Degueldre, H., Metzger, J. J., Geisel, T. & Fleischmann, R. Random focusing of tsunami waves. Nat. Phys. 12, 259–262 (2016).
Wolfson, M. A. & Tomsovic, S. On the stability of long-range sound propagation through a structured ocean. J. Acoust. Soc. Am. 109, 2693–2703 (2001).
Mattheakis, M., Tsironis, G. P. & Kaxiras, E. Emergence and dynamical properties of stochastic branching in the electronic flows of disordered Dirac solids. EPL 122, 27003 (2018).
Mattheakis, M. & Tsironis, G. P. Quodons in mica. In Extreme Waves and Branched Flows in Optical Media 425–454 (Springer International Publishing, 2015).
Mattheakis, M., Pitsios, I. J., Tsironis, G. P. & Tzortzakis, S. Extreme events in complex linear and nonlinear photonic media. Chaos Solitons Fractals 84, 73–80 (2016).
Dudley, J. M., Dias, F., Erkintalo, M. & Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photon. 8, 755–764 (2014).
Akhmediev, N., Soto-Crespo, J. M. & Ankiewicz, A. Extreme waves that appear from nowhere: on the nature of rogue waves. Phys. Lett. A 373, 2137–2145 (2009).
Brandstötter, A., Girschik, A., Ambichl, P. & Rotter, S. Shaping the branched flow of light through disordered media. Proc. Natl Acad. Sci. USA 116, 13260–13265 (2019).
Berry, M. V. & Upstill, C. in Progress in Optics. IV. Catastrophe Optics: Morphologies of Caustics and Their Diffraction Patterns (ed. Wolf, E.) Vol. 18, 257–346 (Elsevier, 1980).
Kaplan, L. Statistics of branched flow in a weak correlated random potential. Phys. Rev. Lett. 89, 184103 (2002).
Kravtsov, Y. A. & Orlov, Y. I. Caustics, Catastrophes and Wave Fields (Springer, 1993).
Patsyk, A., Bandres, M. A. & Segev, M. Interaction of light with thin liquid membranes. In Conference on Lasers and Electro-Optics FF3E2 (Optical Society of America, 2018); https://www.osapublishing.org/abstract.cfm?uri=CLEO_QELS-2019-FTu3D.1.
Metzger, J. J., Fleischmann, R. & Geisel, T. Universal statistics of branched flows. Phys. Rev. Lett. 105, 020601 (2010).
Degueldre, H., Metzger, J. J., Schultheis, E. & Fleischmann, R. Channeling of branched flow in weakly scattering anisotropic media. Phys. Rev. Lett. 118, 024301 (2017).
Metzger, J. J., Fleischmann, R. & Geisel, T. Statistics of extreme waves in random media. Phys. Rev. Lett. 112, 203903 (2014).
Metzger, J. J., Fleischmann, R. & Geisel, T. Intensity fluctuations of waves in random media: what is the semiclassical limit? Phys. Rev. Lett. 111, 013901 (2013).
Schwartz, T., Bartal, G., Fishman, S. & Segev, M. Transport and Anderson localization in disordered two-dimensional photonic lattices. Nature 446, 52–55 (2007).
Ashkin, A., Dziedzic, J. M. & Smith, P. W. Continuous-wave self-focusing and self-trapping of light in artificial Kerr media. Opt. Lett. 7, 276–278 (1982).
Lamhot, Y. et al. Optical control of thermocapillary effects in complex nanofluids. Phys. Rev. Lett. 103, 264503 (2009).
Schley, R. et al. Loss-proof self-accelerating beams and their use in non-paraxial manipulation of particles’ trajectories. Nat. Commun. 5, 5189 (2014).
Heller, E. J., Fleischmann, R. & Kramer, T. Branched flow. Preprint at https://arxiv.org/abs/1910.07086 (2019).
Bekenstein, R., Nemirovsky, J., Kaminer, I. & Segev, M. Shape-preserving accelerating electromagnetic wave packets in curved space. Phys. Rev. X 4, 011038 (2014).
Patsyk, A., Bandres, M. A., Bekenstein, R. & Segev, M. Observation of accelerating wave packets in curved space. Phys. Rev. X 8, 011001 (2018).
Bekenstein, R., Schley, R., Mutzafi, M., Rotschild, C. & Segev, M. Optical simulations of gravitational effects in the Newton–Schrödinger system. Nat. Phys. 11, 872–878 (2015).
El-Ganainy, R., Makris, K. G., Christodoulides, D. N. & Musslimani, Z. H. Theory of coupled optical PT-symmetric structures. Opt. Lett. 32, 2632–2634 (2007).
Acknowledgements
We are indebted to M. V. Berry, for suggesting to us that what we saw in the experiments is related to branched flow. This research was supported by the German-Israeli DIP project, and by the Israel Science Foundation.
Author information
Authors and Affiliations
Contributions
All authors contributed substantially to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, including Supplementary Figures 1-13.
Video 1
Branched flow Typical patterns of branched flow. The light is launched into the soap film through an optical fiber. The optical beam propagates within the thin film, which acts as a slab waveguide with a locally varying thickness. The light scatters from the thickness variations and forms the pattern of branched flow.
Video 2
Branched flow and background potential visualization The video shows branched flow patterns superimposed on top of the landscape of the scattering potential. The system is similar to video #1, but with additional RGB illumination incident upon the film from the top. The RGB light is used to map the thickness fluctuations as a function of position in the plane of the film. The film acts as a Fabry-Perot interferometer for the RGB light, giving rise to the colourful pattern shown in the video. The colours provide the information about the thickness of film as a function of lateral position. From these colours, we calculate the potential landscape, as explained in the SI. The thickness variations in the film act as a weak slowly-varying potential for the laser beam guided within the membrane.
Video 3
Branched flow in curved space In this video, the soap film forms a (semi) spherical bubble, and the branched flow forms within a positively curved 2D shell. In this case, in addition to thickness variations of the film, there is a global curvature of the film that affects the propagation. The curvature acts as an additional focusing potential and makes the branches propagate in a parallel fashion.
Rights and permissions
About this article
Cite this article
Patsyk, A., Sivan, U., Segev, M. et al. Observation of branched flow of light. Nature 583, 60–65 (2020). https://doi.org/10.1038/s41586-020-2376-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2376-8
This article is cited by
-
Isotropic gap formation, localization, and waveguiding in mesoscale Yukawa-potential amorphous structures
Communications Physics (2024)
-
Electrical tuning of branched flow of light
Nature Communications (2024)
-
Optofluidic memory and self-induced nonlinear optical phase change for reservoir computing in silicon photonics
Nature Communications (2023)
-
Multimaterial fiber as a physical simulator of a capillary instability
Nature Communications (2023)
-
Self-organization of photoionized plasmas via kinetic instabilities
Reviews of Modern Plasma Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.