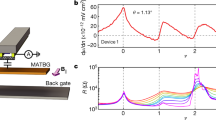
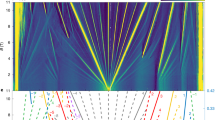
Abstract
Twisted bilayer graphene near the magic angle1,2,3,4 exhibits rich electron-correlation physics, displaying insulating3,4,5,6, magnetic7,8 and superconducting phases4,5,6. The electronic bands of this system were predicted1,2,3,,2 to narrow markedly9,10 near the magic angle, leading to a variety of possible symmetry-breaking ground states11,12,13,14,15,16,17. Here, using measurements of the local electronic compressibility, we show that these correlated phases originate from a high-energy state with an unusual sequence of band population. As carriers are added to the system, the four electronic ‘flavours’, which correspond to the spin and valley degrees of freedom, are not filled equally. Rather, they are populated through a sequence of sharp phase transitions, which appear as strong asymmetric jumps of the electronic compressibility near integer fillings of the moiré lattice. At each transition, a single spin/valley flavour takes all the carriers from its partially filled peers, ‘resetting’ them to the vicinity of the charge neutrality point. As a result, the Dirac-like character observed near charge neutrality reappears after each integer filling. Measurement of the in-plane magnetic field dependence of the chemical potential near filling factor one reveals a large spontaneous magnetization, further substantiating this picture of a cascade of symmetry breaking. The sequence of phase transitions and Dirac revivals is observed at temperatures well above the onset of the superconducting and correlated insulating states. This indicates that the state that we report here, with its strongly broken electronic flavour symmetry and revived Dirac-like electronic character, is important in the physics of magic-angle graphene, forming the parent state out of which the more fragile superconducting and correlated insulating ground states emerge.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots and other analysis in this work are available from the corresponding author upon request.
Code availability
The code used in this work is available at https://github.com/erezberg/Dirac_revivals_theory/ .
Change history
08 July 2020
The online publication date in the printed version of this article was listed incorrectly as 10 June 2020; the date was correct online.
References
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Graphene bilayer with a twist: electronic structure. Phys. Rev. Lett. 99, 256802 (2007).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Suárez Morell, E., Correa, J. D., Vargas, P., Pacheco, M. & Barticevic, Z. Flat bands in slightly twisted bilayer graphene: tight-binding calculations. Phys. Rev. B 82, 121407 (2010).
San-Jose, P., González, J. & Guinea, F. Non-Abelian gauge potentials in graphene bilayers. Phys. Rev. Lett. 108, 216802 (2012).
Po, H. C., Zou, L., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).
Zhang, Y.-H., Po, H. C. & Senthil, T. Landau level degeneracy in twisted bilayer graphene: role of symmetry breaking. Phys. Rev. B 100, 125104 (2019).
Liu, S., Khalaf, E., Lee, J. Y. & Vishwanath, A. Nematic topological semimetal and insulator in magic angle bilayer graphene at charge neutrality. Preprint at http://arXiv.org/abs/1905.07409 (2019).
Po, H. C., Zou, L., Senthil, T. & Vishwanath, A. Faithful tight-binding models and fragile topology of magic-angle bilayer graphene. Phys. Rev. B 99, 195455 (2019).
Xie, M. & MacDonald, A. H. Nature of the correlated insulator states in twisted bilayer graphene. Phys. Rev. Lett. 124, 097601 (2020).
Isobe, H., Yuan, N. F. Q. & Fu, L. Unconventional superconductivity and density waves in twisted bilayer graphene. Phys. Rev. X 8, 041041 (2018).
Ochi, M., Koshino, M. & Kuroki, K. Possible correlated insulating states in magic-angle twisted bilayer graphene under strongly competing interactions. Phys. Rev. B 98, 081102 (2018).
Li, G. et al. Observation of Van Hove singularities in twisted graphene layers. Nat. Phys. 6, 109–113 (2010).
Brihuega, I. et al. Unraveling the intrinsic and robust nature of van Hove singularities in twisted bilayer graphene by scanning tunneling microscopy and theoretical analysis. Phys. Rev. Lett. 109, 196802 (2012).
Wong, D. et al. Local spectroscopy of moiré-induced electronic structure in gate-tunable twisted bilayer graphene. Phys. Rev. B 92, 155409 (2015).
Tomarken, S. L. et al. Electronic compressibility of magic-angle graphene superlattices. Phys. Rev. Lett. 123, 046601 (2019).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019); erratum 15, 1205 (2019).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Cao, Y. et al. Superlattice-induced insulating states and valley-protected orbits in twisted bilayer graphene. Phys. Rev. Lett. 117, 116804 (2016).
Kim, K. et al. van der Waals heterostructures with high accuracy rotational alignment. Nano Lett. 16, 1989–1995 (2016).
Waissman, J. et al. Realization of pristine and locally tunable one-dimensional electron systems in carbon nanotubes. Nat. Nanotechnol. 8, 569–574 (2013).
Honig, M. et al. Local electrostatic imaging of striped domain order in LaAlO3/SrTiO3. Nat. Mater. 12, 1112–1118 (2013).
Yoo, H. et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene. Nat. Mater. 18, 448–453 (2019).
Uri, A. et al. Mapping the twist-angle disorder and Landau levels in magic-angle graphene. Nature 581, 47–52 (2020).
Eisenstein, J., Pfeiffer, L. & West, K. Negative compressibility of interacting two-dimensional electron and quasiparticle gases. Phys. Rev. Lett. 68, 674–677 (1992).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Phys. Rev. Lett. 124, 076801 (2020).
Polshyn, H. et al. Large linear-in-temperature resistivity in twisted bilayer graphene. Nat. Phys. 15, 1011–1016 (2019).
Acknowledgements
We thank U. Aviram, A. H. Macdonald, J. Ruhman, H. Steinberg, S. Todadri, A. Yacoby and E. Zeldov for their suggestions. Work at Weizmann was supported by a Leona M. and Harry B. Helmsley Charitable Trust grant, ISF grants (712539 and 13335/16), a Deloro award, the Sagol Weizmann-MIT Bridge programme, the ERC-Cog (See-1D-Qmatter, no. 647413), ISF Research Grants in the Quantum Technologies and Science Program (994/19 and 2074/19), the DFG (CRC/Transregio 183), the ERC-Cog (HQMAT, no. 817799), EU Horizon 2020 (LEGOTOP 788715) and the Binational Science Foundation (NSF/BMR-BSF grant 2018643). Work at MIT was supported by the National Science Foundation (DMR-1809802), the Center for Integrated Quantum Materials under NSF grant DMR-1231319, and the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF4541 to P.J.-H. for device fabrication, transport measurements and data analysis. This work was performed in part at the Harvard University Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Coordinated Infrastructure Network (NNCI), which is supported by the National Science Foundation under NSF ECCS award no. 1541959. D.R.-L. acknowledges partial support from Fundaciòn Bancaria ‘la Caixa’ (LCF/BQ/AN15/10380011) and from the US Army Research Office (grant no. W911NF-17-S-0001). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, A3 Foresight by JSPS and the CREST (JPMJCR15F3), JST.
Author information
Authors and Affiliations
Contributions
U.Z., A.R., D.R.-L., P.J.-H. and S.I. designed the experiment. U.Z. and A.R. performed the experiments. D.R.-L. and Y.C. fabricated the twisted bilayer graphene devices. U.Z., A.R. and S.I. analysed the data. R.Q., A.R., F.v.O., Y.O., A.S. and E.B. formulated the theory and performed the Hartree-Fock calculations. K.W. and T.T. supplied the hBN crystals. U.Z., A.R., D.R.-L., A.S., E.B., P.J.-H. and S.I. wrote the manuscript, with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Ivan Brihuega, Fan Zhang and Klaus Ensslin for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Sections 1-17, including Supplementary Figures 1-18 and Supplementary References.
Rights and permissions
About this article
Cite this article
Zondiner, U., Rozen, A., Rodan-Legrain, D. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020). https://doi.org/10.1038/s41586-020-2373-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2373-y
This article is cited by
-
Mapping charge excitations in generalized Wigner crystals
Nature Nanotechnology (2024)
-
Layer-polarized ferromagnetism in rhombohedral multilayer graphene
Nature Communications (2024)
-
Spontaneous broken-symmetry insulator and metals in tetralayer rhombohedral graphene
Nature Nanotechnology (2024)
-
Vestigial singlet pairing in a fluctuating magnetic triplet superconductor and its implications for graphene superlattices
Nature Communications (2024)
-
Angle-resolved transport non-reciprocity and spontaneous symmetry breaking in twisted trilayer graphene
Nature Materials (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.