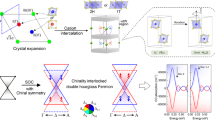
Abstract
Chirality is ubiquitous in nature, and populations of opposite chiralities are surprisingly asymmetric at fundamental levels1,2. Examples range from parity violation in the subatomic weak force to homochirality in biomolecules. The ability to achieve chirality-selective synthesis (chiral induction) is of great importance in stereochemistry, molecular biology and pharmacology2. In condensed matter physics, a crystalline electronic system is geometrically chiral when it lacks mirror planes, space-inversion centres or rotoinversion axes1. Typically, geometrical chirality is predefined by the chiral lattice structure of a material, which is fixed on formation of the crystal. By contrast, in materials with gyrotropic order3,4,5,6, electrons spontaneously organize themselves to exhibit macroscopic chirality in an originally achiral lattice. Although such order—which has been proposed as the quantum analogue of cholesteric liquid crystals—has attracted considerable interest3,4,5,6,7,8,9,10,11,12,13,14,15, no clear observation or manipulation of gyrotropic order has been achieved so far. Here we report the realization of optical chiral induction and the observation of a gyrotropically ordered phase in the transition-metal dichalcogenide semimetal 1T-TiSe2. We show that shining mid-infrared circularly polarized light on 1T-TiSe2 while cooling it below the critical temperature leads to the preferential formation of one chiral domain. The chirality of this state is confirmed by the measurement of an out-of-plane circular photogalvanic current, the direction of which depends on the optical induction. Although the role of domain walls requires further investigation with local probes, the methodology demonstrated here can be applied to realize and control chiral electronic phases in other quantum materials4,16.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Some datasets are available at the Materials Data Facility at https://doi.org/10.18126/r4sn-m7sa.
References
Wagnière, G. H. On Chirality and the Universal Asymmetry: Reflections on Image and Mirror Image (John Wiley & Sons, 2008).
Feringa, B. L. & Van Delden, R. A. Absolute asymmetric synthesis: the origin, control, and amplification of chirality. Angew. Chem. Int. Ed. 38, 3418–3438 (1999).
van Wezel, J. Chirality and orbital order in charge density waves. Europhys. Lett. 96, 67011 (2011).
Hosur, P., Kapitulnik, A., Kivelson, S., Orenstein, J. & Raghu, S. Kerr effect as evidence of gyrotropic order in the cuprates. Phys. Rev. B 87, 115116 (2013).
Orenstein, J. & Moore, J. E. Berry phase mechanism for optical gyrotropy in stripe-ordered cuprates. Phys. Rev. B 87, 165110 (2013).
Fu, L. Parity-breaking phases of spin–orbit-coupled metals with gyrotropic, ferroelectric, and multipolar orders. Phys. Rev. Lett. 115, 026401 (2015).
Ishioka, J. et al. Chiral charge-density waves. Phys. Rev. Lett. 105, 176401 (2010).
Iavarone, M. et al. Evolution of the charge density wave state in CuxTiSe2. Phys. Rev. B 85, 155103 (2012).
Castellan, J.-P. et al. Chiral phase transition in charge ordered 1T-TiSe2. Phys. Rev. Lett. 110, 196404 (2013).
Xia, J. et al. Polar Kerr-effect measurements of the high-temperature YBa2Cu3O6+x superconductor: evidence for broken symmetry near the pseudogap temperature. Phys. Rev. Lett. 100, 127002 (2008).
Hildebrand, B. et al. Local real-space view of the achiral 1T-TiSe2 2 × 2 × 2 charge density wave. Phys. Rev. Lett. 120, 136404 (2018).
Varma, C. Gyrotropic birefringence in the underdoped cuprates. Europhys. Lett. 106, 27001 (2014).
Zenker, B., Fehske, H., Beck, H., Monney, C. & Bishop, A. Chiral charge order in 1T-TiSe2: importance of lattice degrees of freedom. Phys. Rev. B Condens. Matter Mater. Phys. 88, 075138 (2013).
Ganesh, R., Baskaran, G., van den Brink, J. & Efremov, D. V. Theoretical prediction of a time-reversal broken chiral superconducting phase driven by electronic correlations in a single TiSe2 layer. Phys. Rev. Lett. 113, 177001 (2014).
Gradhand, M. & van Wezel, J. Optical gyrotropy and the nonlocal Hall effect in chiral charge-ordered TiSe2. Phys. Rev. B 92, 041111 (2015).
Sugawara, Y. et al. Incommensurate chiral CDW in 1T-VSe2. Preprint at https://arxiv.org/abs/1812.01368 (2018).
Fradkin, E., Kivelson, S. A., Lawler, M. J., Eisenstein, J. P. & Mackenzie, A. P. Nematic fermi fluids in condensed matter physics. Annu. Rev. Condens. Matter Phys. 1, 153–178 (2010).
Armitage, N. Constraints on Jones transmission matrices from time-reversal invariance and discrete spatial symmetries. Phys. Rev. B 90, 035135 (2014).
Hosur, P., Kapitulnik, A., Kivelson, S., Orenstein, J. & Raghu, S. Kerr effect as evidence of gyrotropic order in the cuprates. Phys. Rev. B 91, 039908 (2015).
Kozii, V. & Fu, L. Odd-parity superconductivity in the vicinity of inversion symmetry breaking in spin–orbit-coupled systems. Phys. Rev. Lett. 115, 207002 (2015).
Chang, G. et al. Universal topological electronic properties of nonmagnetic chiral crystals. Nat. Mater. 17, 978–985 (2018).
de Juan, F., Grushin, A. G., Morimoto, T. & Moore, J. E. Quantized circular photogalvanic effect in Weyl semimetals. Nat. Commun. 8, 15995 (2017).
McIver, J., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization. Nat. Nanotechnol. 7, 96–100 (2012).
Kidd, T., Miller, T., Chou, M. & Chiang, T.-C. Electron–hole coupling and the charge density wave transition in TiSe2. Phys. Rev. Lett. 88, 226402 (2002).
Morosan, E. et al. Superconductivity in CuxTiSe2. Nat. Phys. 2, 544–550 (2006).
Li, G. et al. Semimetal-to-semimetal charge density wave transition in 1T-TiSe2. Phys. Rev. Lett. 99, 027404 (2007).
Porer, M. et al. Non-thermal separation of electronic and structural orders in a persisting charge density wave. Nat. Mater. 13, 857–861 (2014).
Chen, P. et al. Charge density wave transition in single-layer titanium diselenide. Nat. Commun. 6, 8943 (2015).
Li, L. et al. Controlling many-body states by the electric-field effect in a two-dimensional material. Nature 529, 185–189 (2016).
Kogar, A. et al. Signatures of exciton condensation in a transition metal dichalcogenide. Science 358, 1314–1317 (2017).
Holt, M., Zschack, P., Hong, H., Chou, M. & Chiang, T.-C. X-ray studies of phonon softening in TiSe2. Phys. Rev. Lett. 86, 3799 (2001).
Kirilyuk, A., Kimel, A. V. & Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 82, 2731–2784 (2010).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Sipe, J. & Shkrebtii, A. Second-order optical response in semiconductors. Phys. Rev. B 61, 5337–5352 (2000).
Hosur, P. Circular photogalvanic effect on topological insulator surfaces: Berry-curvature-dependent response. Phys. Rev. B 83, 035309 (2011).
Morimoto, T. & Nagaosa, N. Topological nature of nonlinear optical effects in solids. Sci. Adv. 2, e1501524 (2016).
Olbrich, P. et al. Observation of the orbital circular photogalvanic effect. Phys. Rev. B 79, 121302 (2009).
Ivchenko, E. & Ganichev, S. in Spin Physics in Semiconductors 245–277 (Springer, 2008).
Plank, H. & Ganechev, S. A review on terahertz photogalvanic spectroscopy of Bi2Te3- and Sb2Te3-based three dimensional topological insulators. Solid-State Electron. 147, 44–50 (2018).
Yuan, H. et al. Generation and electric control of spin–valley-coupled circular photogalvanic current in WSe2. Nat. Nanotechnol. 9, 851–857 (2014).
Dhara, S., Mele, E. J. & Agarwal, R. Voltage-tunable circular photogalvanic effect in silicon nanowires. Science 349, 726–729 (2015).
Ma, Q. et al. Direct optical detection of Weyl fermion chirality in a topological semimetal. Nat. Phys. 13, 842–847 (2017).
Lim, S., Rajamathi, C. R., Süß, V., Felser, C. & Kapitulnik, A. Temperature-induced inversion of the spin-photogalvanic effect in WTe2 and MoTe2. Phys. Rev. B 98, 121301 (2018).
Ji, Z. et al. Spatially dispersive circular photogalvanic effect in a Weyl semimetal. Nat. Mater. 18, 955–962 (2019).
Xu, S.-Y. et al. Electrically switchable Berry curvature dipole in the monolayer topological insulator WTe2. Nat. Phys. 14, 900–906 (2018).
Lakhani, A. A., Jandl, S., Ayache, C. & Jay-Gerin, J.-P. Thermoelectric power of TiSe2-xSx mixed crystals at low temperatures. Phys. Rev. B Condens. Matter 28, 1978–1982 (1983).
Acknowledgements
We thank X. Xu, V. Fatemi, E. J. Sie and S. Fang for discussions. N.G., S.-Y.X., A.K. and A.Z. acknowledge support from the US Department of Energy, Office of Science, Office of Basic Energy Sciences, DMSE (data taking and analysis) and the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF4540 (manuscript writing). Work in P.J.-H. group was supported through AFOSR grant FA9550-16-1-0382 (fabrication and measurement), as well as through the Center for the Advancement of Topological Semimetals, an Energy Frontier Research Center funded by the US Department of Energy Office of Science, Office of Basic Energy Sciences, through the Ames Laboratory under contract DE-AC02-07CH11358 (data analysis), and the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF 4541 to P.J.-H. This work made use of the Materials Research Science and Engineering Center Shared Experimental Facilities supported by the National Science Foundation (NSF) (grant number DMR-0819762). The work at Drexel University was supported by NSF through grant number ECCS-1711015. Research conducted at CHESS is supported by the NSF via awards DMR-1332208 and DMR-1829070. Work at CMU was supported by the Department of Energy, Basic Energy Sciences, Materials Sciences and Engineering Division, through grant number DE-SC0012509. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by MEXT, Japan, JSPS KAKENHI grant numbers JP18K19136 and CREST (JPMJCR15F3), JST. T.-R.C. was supported by the Young Scholar Fellowship Program of the Ministry of Science and Technology (MOST) in Taiwan, under a MOST grant for the Columbus Program MOST108-2636-M-006-002, National Cheng Kung University, Taiwan, and National Center for Theoretical Sciences, Taiwan. This work was supported partially by MOST, Taiwan, via grant MOST107-2627-E-006-001. This research was supported in part by a Higher Education Sprout Project, Ministry of Education from the Headquarters of University Advancement at National Cheng Kung University (NCKU). S.-M.H. acknowledges support by the Ministry of Science and Technology (MoST) in Taiwan under grant number 105-2112-M-110-014-MY3. H.L. acknowledges Academia Sinica, Taiwan for support under Innovative Materials and Analysis Technology Exploration (AS-iMATE-107-11).
Author information
Authors and Affiliations
Contributions
N.G. and P.J.-H. supervised the project. S.-Y.X. and Q.M. conceived the experiment. S.-Y.X. and Q.M. performed photocurrent measurements and analysed the data. A.K., J.P.C.R., S.-Y.X. and Q.M. performed X-ray diffraction measurements. A.M.M.V., T.H.D., Q.M. and S.-Y.X. fabricated the devices. Y.G. and S.-Y.X. performed theoretical analysis under the supervision of D.X. C.-H.H., S.-M.H., B.S. and T.-R.C. performed density functional theory calculations under the supervision of H.L. G.K. grew TiSe2 crystals. K.W. and T.T. grew the bulk h-BN single crystals. A.Z. made significant contributions to the symmetry analysis and the overall presentation. S.-Y.X., Q.M., P.J.-H. and N.G. wrote the manuscript with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Sajal Dhara, Jasper van Wezel and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Polarization-independent photocurrent.
Measured photothermoelectric (PTE) current \({{I}}_{{z}}^{{\rm{PTE}}}\) at different temperatures during heating of the sample from 50 K tow room temperature. The data shown here are from the same photocurrent measurements as those in Fig. 2d, h; they represent the polarization-independent component, whereas those in Fig. 2d, h are the polarization-dependent component of the photocurrent. PTE currents of about 10 nA, 40 nA and 150 nA at 250 K, 170 K and 50 K correspond to a temperature increase of about 2 K, 0.5 K and 0.1 K at 50 K, 170 K and 250 K, respectively, according to the thermopower values measured in ref. 46.
Extended Data Fig. 2 Contrasting behaviours of in-plane and out-of-plane photocurrents as a result of the gyrotropic order in 1T-TiSe2.
a, b, Optical image (a) and schematic illustration (b) of a TiSe2 photoactive device that can detect both the in-plane and out-of-plane photocurrents independently. The electrodes are labelled by capital letters. c, Spatial map of the out-of-plane photocurrent Iz between electrodes G–A at T = 100 K. d, Polarization-dependent Iz data at T = 100 K. The measured photocurrent Iz is consistent with the results of previous devices (Figs. 2, 3). A single peak is observed in c that roughly covers the device. This peak consists of two independent signals: the polarization-independent background, which arises from the photothermoelectric effect and exists at all temperatures, and the polarization-dependent CPGE signal (d), which depends on chiral induction and appears only at low temperatures. e–h, Same as c, d, but for the in-plane photocurrent Ix,y between electrodes C–H (e, f) and C–D (g, h). Ix,y shows distinctly different properties from Iz. No in-plane CPGE is observed (f, h). The polarization-independent signal shows a bipolar spatial configuration (e, g): Ix,y changes sign as the beam spot is scanned from one contact to the other. This bipolar spatial configuration, which has been widely observed in other in-plane photocurrent studies23, further confirms that the polarization-independent signals are photothermoelectric currents at the contact–sample junctions. Scale bars, 25 μm. All data in this figure were collected after RCP chiral induction with an induction power of 30 mW.
Supplementary information
Supplementary Information
This file includes Supplementary Figures S1-S25 and Supplementary Tables S1-S3.
Rights and permissions
About this article
Cite this article
Xu, SY., Ma, Q., Gao, Y. et al. Spontaneous gyrotropic electronic order in a transition-metal dichalcogenide. Nature 578, 545–549 (2020). https://doi.org/10.1038/s41586-020-2011-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2011-8
This article is cited by
-
Chirality manipulation of ultrafast phase switches in a correlated CDW-Weyl semimetal
Nature Communications (2024)
-
Electrical switching of ferro-rotational order in nanometre-thick 1T-TaS2 crystals
Nature Nanotechnology (2023)
-
Berry curvature dipole generation and helicity-to-spin conversion at symmetry-mismatched heterointerfaces
Nature Nanotechnology (2023)
-
Revealing inverted chirality of hidden domain wall states in multiband systems without topological transition
Communications Physics (2023)
-
Chiral phonons in quartz probed by X-rays
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.