Abstract
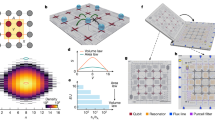
Dualities are mathematical mappings that reveal links between apparently unrelated systems in virtually every branch of physics1,2,3,4,5,6,7,8. Systems mapped onto themselves by a duality transformation are called self-dual and exhibit remarkable properties, as exemplified by the scale invariance of an Ising magnet at the critical point. Here we show how dualities can enhance the symmetries of a dynamical matrix (or Hamiltonian), enabling the design of metamaterials with emergent properties that escape a standard group theory analysis. As an illustration, we consider twisted kagome lattices9,10,11,12,13,14,15, reconfigurable mechanical structures that change shape by means of a collapse mechanism9. We observe that pairs of distinct configurations along the mechanism exhibit the same vibrational spectrum and related elastic moduli. We show that these puzzling properties arise from a duality between pairs of configurations on either side of a mechanical critical point. The critical point corresponds to a self-dual structure with isotropic elasticity even in the absence of spatial symmetries and a twofold-degenerate spectrum over the entire Brillouin zone. The spectral degeneracy originates from a version of Kramers’ theorem16,17 in which fermionic time-reversal invariance is replaced by a hidden symmetry emerging at the self-dual point. The normal modes of the self-dual systems exhibit non-Abelian geometric phases18,19 that affect the semiclassical propagation of wavepackets20, leading to non-commuting mechanical responses. Our results hold promise for holonomic computation21 and mechanical spintronics by allowing on-the-fly manipulation of synthetic spins carried by phonons.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
No external data set was used during the current study.
Code availability
The code used to compute the band structures and the holonomies, to perform the group-theoretical analysis, to integrate the semiclassical equations of motion and to verify the duality relations is available on Zenodo at https://doi.org/10.5281/zenodo.3417426 under the 2-clause BSD licence.
References
Kramers, H. A. & Wannier, G. H. Statistics of the two-dimensional ferromagnet. Part I. Phys. Rev. 60, 252–262 (1941).
Savit, R. Duality in field theory and statistical systems. Rev. Mod. Phys. 52, 453–487 (1980).
Urade, Y., Nakata, Y., Nakanishi, T. & Kitano, M. Frequency-independent response of self-complementary checkerboard screens. Phys. Rev. Lett. 114, 237401 (2015).
Senthil, T., Vishwanath, A., Balents, L., Sachdev, S. & Fisher, M. P. A. Deconfined quantum critical points. Science 303, 1490–1494 (2004).
Louvet, T., Delplace, P., Fedorenko, A. A. & Carpentier, D. On the origin of minimal conductivity at a band crossing. Phys. Rev. B 92, 155116 (2015).
Devetak, I. Triangle of dualities between quantum communication protocols. Phys. Rev. Lett. 97, 140503 (2006).
Hull C. M. & Townsend, P. K. Unity of superstring dualities. Nucl. Phys. B 438, 109–137 (1995).
Maldacena, J. The large-N limit of superconformal field theories and supergravity. Int. J. Theor. Phys. 38, 1113–1133 (1999)
Guest, S. & Hutchinson, J. W. On the determinacy of repetitive structures. J. Mech. Phys. Solids 51, 383–391 (2003).
Souslov, A., Liu, A. J. & Lubensky, T. C. Elasticity and response in nearly isostatic periodic lattices. Phys. Rev. Lett. 103, 205503 (2009).
Sun, K., Souslov, A., Mao, X. & Lubensky, T. C. Surface phonons, elastic response, and conformal invariance in twisted kagome lattices. Proc. Natl Acad. Sci. USA 109, 12369–12374 (2012).
Kane, C. L. & Lubensky, T. C. Topological boundary modes in isostatic lattices. Nat. Phys. 10, 39–45 (2013).
Paulose, J., Gin-ge Chen, B. & Vitelli, V. Topological modes bound to dislocations in mechanical metamaterials. Nat. Phys. 11, 153–156 (2015).
Rocklin, D. Z., Zhou, S., Sun, K. & Mao, X. Transformable topological mechanical metamaterials. Nat. Commun. 8, 14201 (2017).
Ma, J., Zhou, D., Sun, K., Mao, X. & Gonella, S. Edge modes and asymmetric wave transport in topological lattices: experimental characterization at finite frequencies. Phys. Rev. Lett. 121, 094301 (2018).
Kramers, H. A. Théorie générale de la rotation paramagnétique dans les cristaux. Proc. K. Akad. Wet. C 33, 959–972 (1930).
Klein, M. J. On a degeneracy theorem of Kramers. Am. J. Phys. 20, 65–71 (1952).
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. A 392, 45–57 (1984).
Wilczek, F. & Zee, A. Appearance of gauge structure in simple dynamical systems. Phys. Rev. Lett. 52, 2111–2114 (1984).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Zanardi, P. & Rasetti, M. Holonomic quantum computation. Phys. Lett. A 264, 94–99 (1999).
Coleman, S. Aspects of Symmetry (Cambridge Univ. Press, 1985).
Khanikaev, A. B., Fleury, R., Hossein Mousavi, S. & Alù, A. Topologically robust sound propagation in an angular-momentum-biased graphene-like resonator lattice. Nat. Commun. 6, 8260 (2015).
Süsstrunk, R. & Huber, S. D. Classification of topological phonons in linear mechanical metamaterials. Proc. Natl Acad. Sci. USA 113, E4767–E4775 (2016).
Huber, S. D. Topological mechanics. Nat. Phys. 12, 621–623 (2016).
Matlack, K. H., Serra-Garcia, M., Palermo, A., Huber, S. D. & Daraio, C. Designing perturbative metamaterials from discrete models. Nat. Mater. 17, 323–328 (2018).
Fruchart, M. et al. Soft self-assembly of Weyl materials for light and sound. Proc. Natl Acad. Sci. USA 115, E3655–E3664 (2018).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Ningyuan, J., Owens, C., Sommer, A., Schuster, D. & Simon, J. Time- and site-resolved dynamics in a topological circuit. Phys. Rev. X 50, 021031 (2015).
Albert, V. V., Glazman, L. I. & Jiang, L. Topological properties of linear circuit lattices. Phys. Rev. Lett. 114, 173902 (2015).
Lee, C. H. et al. Topolectrical circuits. Commun. Phys. 1, 39 (2018).
Culcer, D., Yao, Y. & Niu, Q. Coherent wave-packet evolution in coupled bands. Phys. Rev. B 72, 085110 (2005).
Shindou, R. & Imura, K.-I. Noncommutative geometry and non-Abelian Berry phase in the wave-packet dynamics of Bloch electrons. Nucl. Phys. B 720, 399–435 (2005).
Onoda, M., Murakami, S. & Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 93, 083901 (2004).
Stern, A. & Lindner, N. H. Topological quantum computation—from basic concepts to first experiments. Science 339, 1179–1184 (2013).
Iadecola, T., Schuster, T. & Chamon, C. Non-Abelian braiding of light. Phys. Rev. Lett. 117, 073901 (2016).
Barlas, Y. & Prodan, E. Topological braiding of Majorana-like modes in classical metamaterials. Preprint at https://arxiv.org/abs/1903.00463 (2019).
Liu, Y., Liu, Y. & Prodan, E. Braiding flux-tubes in topological quantum and classical lattice models from class-D. Preprint at https://arxiv.org/abs/1905.02457 (2019).
Li, N.et al. Phononics: manipulating heat flow with electronic analogs and beyond. Rev. Mod. Phys. 84, 1045–1066 (2012).
Wilczek, F. & Shapere, A. Geometric Phases in Physics (World Scientific, 1989).
Chruściński, D. & Jamiołkowski, A. Geometric Phases in Classical and Quantum Mechanics (Birkhäuser Boston, 2004).
Cohen, E. et al. Geometric phase from Aharonov–Bohm to Pancharatnam–Berry and beyond. Nat. Rev. Phys. 1, 437–449 (2019).
Wu, T. T. & Yang, C. N. Concept of nonintegrable phase factors and global formulation of gauge fields. Phys. Rev. D 12, 3845–3857 (1975).
Wilson, K. G. Confinement of quarks. Phys. Rev. D 10, 2445–2459 (1974).
Bliokh, K. Y. & Bliokh, Y. P. Modified geometrical optics of a smoothly inhomogeneous isotropic medium: the anisotropy, Berry phase, and the optical Magnus effect. Phys. Rev. E 70, 026605 (2004).
Onoda, M., Murakami, S. & Nagaosa, N. Geometrical aspects in optical wave-packet dynamics. Phys. Rev. E 74, 066610 (2006).
Bliokh, K. Y., Frolov D. Y. & Kravtsov Y. A. Non-Abelian evolution of electromagnetic waves in a weakly anisotropic inhomogeneous medium. Phys. Rev. A 75, 053821 (2007).
Bliokh, K. Y. & Freilikher, V. D. Polarization transport of transverse acoustic waves: Berry phase and spin Hall effect of phonons. Phys. Rev. B 74, 174302 (2006).
Mehrafarin, M. &Torabi, R. Geometric aspects of phonon polarization transport. Phys. Lett. A 373, 2114–2116 (2009).
Torabi, R. & Mehrafarin M. Berry effect in acoustical polarization transport in phononic crystals. JETP Lett. 88, 590–594 (2009).
Alden Mead, C. Molecular Kramers degeneracy and non-Abelian adiabatic phase factors. Phys. Rev. Lett. 59, 161–164 (1987).
Zee, A. Non-Abelian gauge structure in nuclear quadrupole resonance. Phys. Rev. A 38, 1–6 (1988).
Alden Mead, C. The geometric phase in molecular systems. Rev. Mod. Phys. 64, 51–85 (1992).
Sugawa, S., Salces-Carcoba, F., Perry, A. R., Yue, Y. & Spielman, I. B. Second Chern number of a quantum-simulated non-Abelian Yang monopole. Science 360, 1429–1434 (2018).
Bliokh, K. Y. Rodriguez-Fortuño, F. J. Nori, F. & Zayats, A. V. Spin–orbit interactions of light. Nat. Photonics 9, 796–808 (2015).
Ma, L. B. et al. Spin–orbit coupling of light in asymmetric microcavities. Nat. Commun. 7, 10983 (2016).
Dalibard, J., Gerbier, F., Juzeliūnas, G. & Öhberg, P. Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 83, 1523–1543 (2011).
Goldman, N., Juzeliūnas, G., Öhberg, P. & Spielman, I. B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 77, 126401 (2014).
Wu, Z. et al. Realization of two-dimensional spin–orbit coupling for Bose–Einstein condensates. Science 354, 83–88 (2016).
Huang, L. et al. Experimental realization of two-dimensional synthetic spin–orbit coupling in ultracold Fermi gases. Nat. Phys. 12, 540–544 (2016).
Aidelsburger, M., Nascimbene, S. & Goldman, N. Artificial gauge fields in materials and engineered systems. C. R. Phys. 19, 394–432 (2018).
Chen, Y. et al. Non-Abelian gauge field optics. Nat. Commun. 10, 3125 (2019).
Yang, Y. et al. Synthesis and observation of non-Abelian gauge fields in real space. Science 365, 1021–1025 (2019).
Leinaas, J. M. & Myrheim, J. On the theory of identical particles. Nuovo Cimento B 37, 1–23 (1977).
Wilczek, F. Quantum mechanics of fractional-spin particles. Phys. Rev. Lett. 49, 957–959 (1982).
Fröhlich, J. in Nonperturbative Quantum Field Theory (eds ’t Hooft, G. et al.) 71–100 (Springer, 1988).
Wen, X. G. Non-Abelian statistics in the fractional quantum Hall states. Phys. Rev. Lett. 66, 802–805 (1991).
Moore, G. & Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 360, 362–396 (1991).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Arovas, D., Schrieffer, J. R. & Wilczek, F. Fractional statistics and the quantum Hall effect. Phys. Rev. Lett. 53, 722–723 (1984).
Lahtinen, V. & Pachos, J. K. Non-Abelian statistics as a Berry phase in exactly solvable models. New J. Phys. 11, 093027 (2009).
Noh, J. et al. Braiding photonic topological zero modes. Preprint at https://arxiv.org/abs/1907.03208 (2019).
Maldovan, M. Sound and heat revolutions in phononics. Nature 503, 209–217 (2013).
Born, M. et al. Principles of Optics (Cambridge Univ. Press, 1999).
Karplus, R. & Luttinger, J. M. Hall effect in ferromagnetics. Phys. Rev. 95, 1154–1160 (1954).
Chang, M.-C. & Niu, Q. Berry phase, hyperorbits, and the Hofstadter spectrum: semiclassical dynamics in magnetic Bloch bands. Phys. Rev. B 53, 7010–7023 (1996).
Sundaram, G. & Niu, Q. Wave-packet dynamics in slowly perturbed crystals: gradient corrections and Berry-phase effects. Phys. Rev. B 59, 14915–14925 (1999).
Panati, G., Spohn, H. & Teufel, S. Effective dynamics for Bloch electrons: Peierls substitution and beyond. Commun. Math. Phys. 242, 547–578 (2003).
Chang, M.-C. & Niu, Q. Berry curvature, orbital moment, and effective quantum theory of electrons in electromagnetic fields. J. Phys. Condens. Matter 20, 193202 (2008).
Zener, C. A theory of the electrical breakdown of solid dielectrics. Proc. R. Soc. A 145, 523–529 (1934).
Mendez, E. E. & Bastard, G. Wannier–Stark ladders and Bloch oscillations in superlattices. Phys. Today 46, 34–42 (1993).
Raizen, M., Salomon, C. & Niu, Q. New light on quantum transport. Phys. Today 50, 30–34 (1997).
Price, H. M. & Cooper, N. R. Mapping the Berry curvature from semiclassical dynamics in optical lattices. Phys. Rev. A 85, 033620 (2012).
Atala, M. et al. Direct measurement of the Zak phase in topological Bloch bands. Nat. Phys. 9, 795–800 (2013).
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237–240 (2014).
Aidelsburger, M. et al. Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms. Nat. Phys. 11, 162–166 (2014).
Flaschner, N. et al. Experimental reconstruction of the Berry curvature in a Floquet Bloch band. Science 352, 1091–1094 (2016).
Li, T. et al. Bloch state tomography using Wilson lines. Science 352, 1094–1097 (2016).
Acknowledgements
We thank B. Bradlyn, V. Cheianov, S. Huber, W. Irvine, P. Lidon, N. Mitchell, S. Ryu, C. Scheibner, D. Son, A. Souslov, P. Wiegmann and B. van Zuiden for discussions. V.V. was supported by the Complex Dynamics and Systems Program of the Army Research Office under grant no. W911NF-19-1-0268. M.F. was primarily supported by the Chicago MRSEC (US NSF grant DMR 1420709) through a Kadanoff–Rice postdoctoral fellowship and acknowledges partial support by the University of Chicago through a Big Ideas Generator (BIG) grant and the Netherlands Organization for Scientific Research (NWO/OCW) as part of the Frontiers of Nanoscience program. LEGO is a trademark of the LEGO Group of companies which does not sponsor, license or endorse its use in this work.
Author information
Authors and Affiliations
Contributions
M.F. and V.V. designed the research, performed the research, and wrote the paper. Y.Z. and M.F. fabricated the mechanical kagome lattices. All authors contributed to discussions and manuscript revision.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Muamer Kadic, Ronny Thomale and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Notes: contains supplementary information about the system, the derivation, and the numerical simulations.
Video 1
Video demonstrating the zero-energy mechanism and its relation with the duality.
Rights and permissions
About this article
Cite this article
Fruchart, M., Zhou, Y. & Vitelli, V. Dualities and non-Abelian mechanics. Nature 577, 636–640 (2020). https://doi.org/10.1038/s41586-020-1932-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-1932-6
This article is cited by
-
Strain topological metamaterials and revealing hidden topology in higher-order coordinates
Nature Communications (2023)
-
Non-orientable order and non-commutative response in frustrated metamaterials
Nature (2023)
-
General duality and magnet-free passive phononic Chern insulators
Nature Communications (2023)
-
A second wave of topological phenomena in photonics and acoustics
Nature (2023)
-
Orbital topological edge states and phase transitions in one-dimensional acoustic resonator chains
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.