Abstract
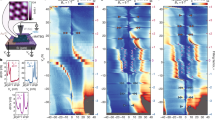
Magic-angle twisted bilayer graphene (MATBG) exhibits a range of correlated phenomena that originate from strong electron–electron interactions. These interactions make the Fermi surface highly susceptible to reconstruction when ±1, ±2 and ±3 electrons occupy each moiré unit cell, and lead to the formation of various correlated phases1,2,3,4. Although some phases have been shown to have a non-zero Chern number5,6, the local microscopic properties and topological character of many other phases have not yet been determined. Here we introduce a set of techniques that use scanning tunnelling microscopy to map the topological phases that emerge in MATBG in a finite magnetic field. By following the evolution of the local density of states at the Fermi level with electrostatic doping and magnetic field, we create a local Landau fan diagram that enables us to assign Chern numbers directly to all observed phases. We uncover the existence of six topological phases that arise from integer fillings in finite fields and that originate from a cascade of symmetry-breaking transitions driven by correlations7,8. These topological phases can form only for a small range of twist angles around the magic angle, which further differentiates them from the Landau levels observed near charge neutrality. Moreover, we observe that even the charge-neutrality Landau spectrum taken at low fields is considerably modified by interactions, exhibits prominent electron–hole asymmetry, and features an unexpectedly large splitting between zero Landau levels (about 3 to 5 millielectronvolts). Our results show how strong electronic interactions affect the MATBG band structure and lead to correlation-enabled topological phases.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2019).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Wong, D. et al. Cascade of transitions between the correlated electronic states of magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).
Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Graphene bilayer with a twist: electronic structure. Phys. Rev. Lett. 99, 256802 (2007).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013).
Ponomarenko, L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).
Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).
Wang, L. et al. Evidence for a fractional fractal quantum Hall effect in graphene superlattices. Science 350, 1231–1234 (2015).
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).
Bistritzer, R. & MacDonald, A. H. Moiré butterflies in twisted bilayer graphene. Phys. Rev. B 84, 035440 (2011).
Arora, H. S. et al. Superconductivity in metallic twisted bilayer graphene stabilized by WSe2. Nature 583, 379–384 (2020).
Brihuega, I. et al. Unraveling the intrinsic and robust nature of van Hove singularities in twisted bilayer graphene by scanning tunneling microscopy and theoretical analysis. Phys. Rev. Lett. 109, 196802 (2012).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019); author correction 15, 1205 (2019).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Jung, S. et al. Evolution of microscopic localization in graphene in a magnetic field from scattering resonances to quantum dots. Nat. Phys. 7, 245–251 (2011).
Po, H. C., Zou, L., Senthil, T. & Vishwanath, A. Faithful tight-binding models and fragile topology of magic-angle bilayer graphene. Phys. Rev. B 99, 195455 (2019).
Uri, A. et al. Mapping the twist-angle disorder and Landau levels in magic-angle graphene. Nature 581, 47–52 (2020).
Saito, Y. et al. Hofstadter subband ferromagnetism and symmetry broken Chern insulators in twisted bilayer graphene. Preprint at https://arxiv.org/abs/2007.06115 (2020).
Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators and topological flat-bands in magic-angle twisted bilayer graphene. Preprint at https://arxiv.org/abs/2007.03735 (2020).
Das, I. et al. Symmetry broken Chern insulators and magic series of Rashba-like Landau level crossings in magic angle bilayer graphene. Preprint at https://arxiv.org/abs/2007.13390 (2020).
Wannier, G. H. A result not dependent on rationality for Bloch electrons in a magnetic field. Phys. Stat. Sol. B 88, 757–765 (1978).
Guinea, F. & Walet, N. R. Electrostatic effects, band distortions, and superconductivity in twisted graphene bilayers. Proc. Natl Acad. Sci. USA 115, 13174–13179 (2018).
Goodwin, Z. A. H., Vitale, V., Liang, X., Mostofi, A. A. & Lischner, J. Hartree theory calculations of quasiparticle properties in twisted bilayer graphene. Electron. Struct. 2, 034001 (2020).
Xie, M. & MacDonald, A. H. Nature of the correlated insulator states in twisted bilayer graphene. Phys. Rev. Lett. 124, 097601 (2020).
Bi, Z., Yuan, N. F. Q. & Fu, L. Designing flat bands by strain. Phys. Rev. B 100, 035448 (2019).
Nam, N. N. T. & Koshino, M. Lattice relaxation and energy band modulation in twisted bilayer graphene. Phys. Rev. B 96, 075311 (2017).
Hejazi, K., Liu, C. & Balents, L. Landau levels in twisted bilayer graphene and semiclassical orbits. Phys. Rev. B 100, 035115 (2019).
Zhang, Y.-H., Po, H. C. & Senthil, T. Landau level degeneracy in twisted bilayer graphene: role of symmetry breaking. Phys. Rev. B 100, 125104 (2019).
Carr, S., Fang, S., Po, H. C., Vishwanath, A. & Kaxiras, E. Derivation of Wannier orbitals and minimal-basis tight-binding Hamiltonians for twisted bilayer graphene: first-principles approach. Phys. Rev. Res. 1, 033072 (2019).
Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Walkup, D. et al. Tuning single-electron charging and interactions between compressible Landau level islands in graphene. Phys. Rev. B 101, 035428 (2020).
Wang, T., Bultinck, N. & Zaletel, M. P. Flat band topology of magic angle graphene on a transition metal dichalcogenide. Phys. Rev. B 102, 235146 (2020).
Yin, J.-X. et al. Quantum-limit Chern topological magnetism in TbMn6Sn6. Nature 583, 533–536 (2020).
Gusynin, V. P. & Sharapov, S. G. Unconventional integer quantum Hall effect in graphene. Phys. Rev. Lett. 95, 146801 (2005).
Hatsugai, Y., Fukui, T. & Aoki, H. Topological aspects of graphene. Eur. Phys. J. Spec. Top. 148, 133–141 (2007).
Acknowledgements
We acknowledge discussions with A. Young, G. Refael and S. Mashhadi. The device nanofabrication was performed at the Kavli Nanoscience Institute (KNI) at Caltech. This work was supported by NSF through grants DMR-2005129 and DMR-1723367 and by the Army Research Office under grant award W911NF-17-1-0323. Part of the initial STM characterization was supported by CAREER DMR-1753306. Nanofabrication performed by Y.Z. was supported by the DOE-QIS programme (DE-SC0019166). J.A. and S.N.-P. also acknowledge the support of IQIM (an NSF Physics Frontiers Center with support of the Gordon and Betty Moore Foundation through grant GBMF1250). Y.P. acknowledges support from a startup fund from California State University, Northridge. A.T., C.L. and J.A. are grateful for support from the Walter Burke Institute for Theoretical Physics at Caltech and the Gordon and Betty Moore Foundation’s EPiQS Initiative, grant GBMF8682. Y.C. and H.K. acknowledge support from the Kwanjeong fellowship.
Author information
Authors and Affiliations
Contributions
Y.C. and H.K. fabricated samples with the help of R.P., Y.Z. and H.A., and performed STM measurements. Y.C., H.K. and S.N.-P. analysed the data. Y.P. and A.T. implemented the models. Y.P., A.T. and C.L. provided theoretical analysis, supervised by J.A.; K.W. and T.T. provided materials (hBN). S.N-P. supervised the project. Y.C., H.K, Y.P., A.T., C.L., J.A. and S.N-P. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Vincent Renard, Yayu Wang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
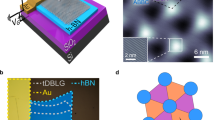
Extended Data Fig. 1 Optical image of the device and STM topography of WSe2/hBN boundary.
a, Optical image of the device. The blue dashed line indicates the region with twisted bilayer graphene (TBG). b, STM topography of a WSe2 boundary underneath twisted bilayer graphene (Vbias = −400 mV, I = 20 pA). c, Linecut along the yellow dashed line in b. The height difference is around 0.8 nm, which matches the monolayer WSe2 thickness. Small ripples originate from the moiré pattern.
Extended Data Fig. 2 AA site point spectra versus gate voltage with magnetic field.
a, B = 0 T. b, B = 4 T. c, B = 8 T. The area (with θ = 1.03°) is the same as that shown in Fig. 1c–e. The VHSs are more pronounced compared to the AB site, making LL features harder to resolve.
Extended Data Fig. 3 Evolution of cascade with magnetic field.
a–e, Point spectra versus gate voltage on an AB site (θ = 1.03°) at B = 4 T (a), B = 5 T (b), B = 6 T (c), B = 7 T (d) and B = 8 T (e). Coloured dashed lines indicate positions calculated with the corresponding Chern numbers. f, Tracking of cascades on the conduction band at different magnetic fields. As the field is increased, the shifting of cascade onsets follows the evolution of Chern insulators. a and e show the same data as Fig. 1d, e; b–d are at intermediate fields on the same area.
Extended Data Fig. 4 Quantum Hall ferromagnetic states at the zLL.
a, Point spectra on an AB site at θ = 1.01° as a function of Vgate for magnetic field B = 7 T. b, Zoom-in around the CNP, where zLLs (0+ and 0−) cross the Fermi energy. The fourfold degeneracy of each zLL is broken by exchange interactions at the Fermi energy, creating gaps at νLL = −4, −3,…, +4. c, Linecuts obtained when the 0− and 0+ LLs cross the Fermi energy, with vertical offset for clarity. Shifting of the spectral weight of the fourfold-degenerate 0− and 0+ LLs cross the Fermi level is clearly visible. Numbers in blue (red) correspond to the number of spin–valley flavours of 0− (0+) LLs below and above the Fermi level (Vbias = 0) as they cross EF near νLL = 4, 3, 2, 1, 0, −1, −2, −3, −4.
Extended Data Fig. 5 Chern insulating phases in the valence band.
a, Full gate voltage range of Fig. 2d at B = 7 T, from ν = −4 to ν = 4. b–g, Zoom-in of Extended Data Fig. 5a around C = −3 (b), C = −2 (d) and C = −1 (f), and the corresponding linecuts (c, e, g) at various Vgate values with vertical offset. Shifting of the spectral weight across the Fermi level is clearly visible in c and e. The C = −1 state is not visible at this angle (θ = 1.02°) and this magnetic field (B = 7 T).
Extended Data Fig. 6 C = −1 phase in a high-resolution angle-dependent LDOS map at B = 7 T.
Measurements were taken over a 20 nm × 200 nm area in which the twist angle varies continuously from θ = 1.01° to 1.18° by using Vbias = 0 mV and changing the spatial position and carrier density (Vgate). The signature of the C = −1 phase and νLL = ±1, ±3, which are not visible in Fig. 3b, are now observed owing to the enhanced Vgate resolution, and the electron–hole asymmetry between Chern phases is even more pronaunced. We note that the visibility of νLL = ±1, ±3 shows strong spatial dependence, whereas the visibility of νLL = ±2, ±4 is high throughout the range.
Extended Data Fig. 7 Spectrum of a continuum model taking into account the effects of a displacement field.
a–c, The spectra correspond to twist angles of θ = 1.03° (a), θ = 1.06° (b) and θ = 1.09° (c). The displacement field, expressed as an energy difference between the two graphene monolayers, is 10 meV, and the ratio between AA and AB tunnelling amplitudes, w0/w1 = 0.4, is the same for all results. A similar spectrum is obtained for larger w0/w1 ratios. The simple continuum model, known to predict correct trends, can capture energetically offset Dirac cones by including a displacement field. However, it underestimates the bandwidth of the flat bands (or equivalently the separation between VHSs) and exhibits an unrealistically strong dependence on the twist angle; even at angles slightly far from the magic angle (θ = 1.06−1.09°), the model predicts a 2−4 times smaller bandwidth than that observed in the data. All spectra feature a well separated LL starting from each band edge that moves inwards with the field. This LL originates from the pocket near the centre of the moiré Brillouin zone and was not observed in the experiment. The bandwidth We (Wh) corresponding to the conductance (valence) flat VHS sub-band is used for estimating the U/W values in Extended Data Fig. 8.
Extended Data Fig. 8 Estimated ratio between correlation and kinetic-energy scales, U/W, as a function of twist angle and magnetic field.
a, b, Estimates from the continuum model for the conduction (a) and valence (b) bands for w0/w1 = 0.4. c, d, The same calculation for w0/w1 = 0.7. e, Analytical estimate from equation (2). The bandwidth in a, b,c,d is evaluated as the total width of all levels that comprise the sub-band that includes the VHS (and carry C = −1 Chern number). Points very close to the magic angle are not shown owing to a lack of clear energy separation from adjacent levels. The plotted constant-U/W curves outline regions where U/W exceeds a threshold value, and qualitatively reproduce the structure of the experimental phase diagram in which Chern insulating phases are observed (Fig. 3f). In e, the large η values are necessary to compensate for the crude approximation of the bandwidth from equation (3), which underestimates the bandwidth compared to the numerical simulation in a, b,c,d.
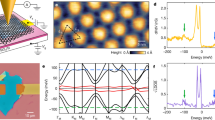
Extended Data Fig. 9 Possible MATBG band-structure scenarios obtained using the ten-band model and corresponding LL spectra.
a, b, Scenario (i); c, d, scenario (ii); e, f, scenario (iii); g, h, scenario (iv) (see Methods section ‘LL spectrum for low fields and MATBG band structure’). The inset in a shows the relevant high-symmetry momenta in the moiré Brillouin zone. Colours in b, d, f and h represent the normalized density of states (DOS) obtained via Lorentzian broadening of the Landau spectrum by 0.3 meV. i, A possible fit to the data in Fig. 4j corresponding to scenario (ii), yielding vD1 = 2.3 × 105 m s−1 and vD2 = 1.9 × 105 m s−1 for the LLs originating from two two Dirac cones (here marked with red and blue solid lines). The dashed lines correspond to expected LLs that were not observed, possibly owing to the relative positions of the Dirac cones with respect to the VHS. We note that this fitting scenario is not unique. However, all analysed scenarios give vD that exceeds 105 m s−1.
Extended Data Fig. 10 Landau fan diagram overlaid on experimental data for different choices of gate voltages corresponding to ν = ±4.
a, LDOS Landau fan with the same gate voltages Vν=−4 and Vν=4, corresponding to ν = ±4, as in Fig. 2c. The same gate voltages (Vν=−4 = −5.6 V and Vν=4 = 6.2 V) are used in b and d. b, c, LDOS Landau fan zoomed-in around the hole-side dispersive band with different choice of gate voltages. The choice in c (Vν=−4 = −5.7 V and Vν=4 = 6.2 V) does not reproduce the data well. d, e, Similar comparison around the CNP, where e corresponds to Vν=−4 = –5.7 V and Vν=4 = 6.3 V. From this comparison, we extract the error in determining ν = ±4 to be 0.1 V. All LDOS data are normalized by an average LDOS value for each magnetic field. f, Linecut of the LDOS fan in a along the LL filling of −2 emanating from ν = −2, averaged over a Vgate window of 0.04 V. The state above B = 6 T that we identify as a Chern insulating phase is distinguished from half-filling LLs by the abrupt drop in LDOS.
Supplementary information
Supplementary Information
The file includes the continuum and ten-band model details that are used to calculate the spectrum in Fig. 1g, Extended Data Fig. 7, Extended Data Fig. 8 and Extended Data Fig. 9.
Rights and permissions
About this article
Cite this article
Choi, Y., Kim, H., Peng, Y. et al. Correlation-driven topological phases in magic-angle twisted bilayer graphene. Nature 589, 536–541 (2021). https://doi.org/10.1038/s41586-020-03159-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-03159-7
This article is cited by
-
Imaging moiré excited states with photocurrent tunnelling microscopy
Nature Materials (2024)
-
Tuning commensurability in twisted van der Waals bilayers
Nature (2024)
-
Tunable moiré materials for probing Berry physics and topology
Nature Reviews Materials (2024)
-
Local spectroscopy of a gate-switchable moiré quantum anomalous Hall insulator
Nature Communications (2023)
-
Dirac spectroscopy of strongly correlated phases in twisted trilayer graphene
Nature Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.