Abstract
Carbon is the fourth-most prevalent element in the Universe and essential for all known life. In the elemental form it is found in multiple allotropes, including graphite, diamond and fullerenes, and it has long been predicted that even more structures can exist at pressures greater than those at Earth’s core1,2,3. Several phases have been predicted to exist in the multi-terapascal regime, which is important for accurate modelling of the interiors of carbon-rich exoplanets4,5. By compressing solid carbon to 2 terapascals (20 million atmospheres; more than five times the pressure at Earth’s core) using ramp-shaped laser pulses and simultaneously measuring nanosecond-duration time-resolved X-ray diffraction, we found that solid carbon retains the diamond structure far beyond its regime of predicted stability. The results confirm predictions that the strength of the tetrahedral molecular orbital bonds in diamond persists under enormous pressure, resulting in large energy barriers that hinder conversion to more-stable high-pressure allotropes1,2, just as graphite formation from metastable diamond is kinetically hindered at atmospheric pressure. This work nearly doubles the highest pressure at which X-ray diffraction has been recorded on any material.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The source data shown in the figures are provided, where not already summarized in Extended Data Table 1. Additional data are available from the corresponding author upon request. Source data are provided with this paper.
Code availability
The data analysis code implementing the methods described in ref. 25 is publicly available at https://github.com/HEXRD.
Change history
21 April 2022
A Correction to this paper has been published: https://doi.org/10.1038/s41586-022-04751-9
References
Scandolo, S., Chiarotti, G. L. & Tosatti, E. SC4: a metallic phase of carbon at terapascal pressures. Phys. Rev. B 53, 5051–5054 (1996).
Sun, J., Klug, D. D. & Martoňák, R. Structural transformations in carbon under extreme pressure: beyond diamond. J. Chem. Phys. 130, 194512 (2009).
Martinez-Canales, M., Pickard, C. J. & Needs, R. J. Thermodynamically stable phases of carbon at multiterapascal pressures. Phys. Rev. Lett. 108, 045704 (2012).
Madhusudhan, N., Lee, K. K. M. & Mousis, O. A possible carbon-rich interior in super-earth 55 Cancri e. Astrophys. J. 759, L40 (2012).
Mashian, N. & Loeb, A. CEMP stars: possible hosts to carbon planets in the early universe. Mon. Not. R. Astron. Soc. 460, 2482–2491 (2016).
Frondel, C. & Marvin, U. B. Lonsdaleite, a hexagonal polymorph of diamond. Nature 214, 587–589 (1967).
Narayan, J. & Bhaumik, A. Novel phase of carbon, ferromagnetism, and conversion into diamond. J. Appl. Phys. 118, 215303 (2015).
Johnston, R. L. & Hoffmann, R. Superdense carbon, C8: supercubane or analog of γ-silicon? J. Am. Chem. Soc. 111, 810–819 (1989).
Mailhiot, C. & McMahan, A. K. Atmospheric-pressure stability of energetic phases of carbon. Phys. Rev. B 44, 11578–11591 (1991).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J. Chem. Phys. 124, 244704 (2006).
Oganov, A. R., Hemley, R. J., Hazen, R. M. & Jones, A. P. Structure, bonding, and mineralogy of carbon at extreme conditions. Rev. Mineral. Geochem. 75, 47–77 (2013).
Yin, M. T. & Cohen, M. L. Will diamond transform under megabar pressures? Phys. Rev. Lett. 50, 2006–2009 (1983).
Biswas, R. & Martin, R. M., Needs, R. J. & Nielsen, O. H. Stability and electronic proper- ties of complex structures of silicon and carbon under pressure: density-functional calculations. Phys. Rev. B 35, 9559–9568 (1987).
Fahy, S. & Louie, S. G. High-pressure structural and electronic properties of carbon. Phys. Rev. B 36, 3373–3385 (1987).
Dubrovinsky, L., Dubrovinskaia, N., Prakapenka, V. B. & Abakumov, A. M. Implementation of micro-ball nanodiamond anvils for high-pressure studies above 6 Mbar. Nat. Commun. 3, 1163 (2012).
Wu, H., Luo, X., Wen, L., Sun, H. & Chen, C. Extreme static compression of carbon to terapascal pressures. Carbon 144, 161–170 (2019).
Eggert, J. H. et al. Melting temperature of diamond at ultrahigh pressure. Nat. Phys. 6, 40–43 (2010).
Swift, D. C. Numerical solution of shock and ramp compression for general material properties. J. Appl. Phys. 104, 073536 (2008).
Smith, R. F. et al. Ramp compression of diamond to five terapascals. Nature 511, 330–333 (2014).
Knudson, M. D., Desjarlais, M. P. & Dolan, D. H. Shock-wave exploration of the high-pressure phases of carbon. Science 322, 1822–1825 (2008).
Barrios, M. A. et al. X-ray area backlighter development at the National Ignition Facility. Rev. Sci. Instrum. 85, 11D502 (2014).
Coppari, F. et al. Optimized x-ray sources for x-ray diffraction measurements at the Omega Laser Facility. Rev. Sci. Instrum. 90, 125113 (2019).
Wark, J. S., Whitlock, R. R., Hauer, A. A., Swain, J. E. & Solone, P. J. Subnanosecond x-ray diffraction from laser-shocked crystals. Phys. Rev. B 40, 5705–5714 (1989).
Rygg, J. R. et al. Powder diffraction from solids in the terapascal regime. Rev. Sci. Instrum. 83, 113904 (2012).
Rygg, J. R. et al. X-ray diffraction at the National Ignition Facility. Rev. Sci. Instrum. 91, 043902 (2020).
Celliers, P. M. et al. Line-imaging velocimeter for shock diagnostics at the OMEGA laser facility. Rev. Sci. Instrum. 75, 4916–4929 (2004).
Rothman, S. D. et al. Measurement of the principal isentropes of lead and lead–antimony alloy to ~400 kbar by quasi-isentropic compression. J. Phys. D 38, 733–740 (2005).
Bradley, D. K. et al. Diamond at 800 GPa. Phys. Rev. Lett. 102, 075503 (2009).
Coppari, F. et al. Experimental evidence for a phase transition in magnesium oxide at exoplanet pressures. Nat. Geosci. 6, 926–929 (2013).
Nelmes, R. J., McMahon, M. I., Wright, N. G., Allan, D. R. & Loveday, J. S. Stability and crystal structure of BC8 germanium. Phys. Rev. B 48, 9883–9886 (1993).
Kurakevych, O. O. et al. Synthesis of bulk BC8 silicon allotrope by direct transformation and reduced-pressure chemical pathways. Inorg. Chem. 55, 8943–8950 (2016).
Turneaure, S. J., Sharma, S. M., Volz, T. J., Winey, J. M. & Gupta, Y. M. Transformation of shock-compressed graphite to hexagonal diamond in nanoseconds. Sci. Adv. 3, eaao3561 (2017).
McWilliams, R. S. et al. Strength effects in diamond under shock compression from 0.1 to 1 TPa. Phys. Rev. B 81, 014111 (2010).
Orlikowski, D., Correa, A. A., Schwegler, E. & Klepeis, J. E. A Steinberg-Guinan model for high-pressure carbon: diamond phase. AIP Conf. Proc. 955, 247–250 (2007).
Swift, D. C. et al. Equation of state and strength of diamond in high pressure ramp loading. Preprint at https://arxiv.org/abs/2004.03071 (2020).
Lang, J. M., Winey, J. M. & Gupta, Y. M. Strength and deformation of shocked diamond single crystals: orientation dependence. Phys. Rev. B 97, 104106 (2018).
Taylor, G. I. & Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. Lond. A 143, 307–326 (1934).
Suggit, M. J. et al. Nanosecond white-light Laue diffraction measurements of dislocation microstructure in shock-compressed single-crystal copper. Nat. Commun. 3, 1224 (2012).
Heighway, P. G. et al. Nonisentropic release of a shocked solid. Phys. Rev. Lett. 123, 245501 (2019).
Ping, Y. et al. Solid iron compressed up to 560 GPa. Phys. Rev. Lett. 111, 065501 (2013).
Murphy, W. J., Higginbotham, A., Wark, J. S. & Park, N. Molecular dynamics simulations of the Debye-Waller effect in shocked copper. Phys. Rev. B 78, 014109 (2008).
Ertel, K. et al. DiPOLE: A scalable laser architecture for pumping multi-Hz PW systems. Proc. SPIE 8780, 288–292 (2013).
Pellegrini, C. X-ray free-electron lasers: from dreams to reality. Phys. Scr. T169, 014004 (2016).
McBride, E. E. et al. Setup for meV-resolution inelastic x-ray scattering measurements and x-ray diffraction at the matter in extreme conditions endstation at the Linac Coherent Light Source. Rev. Sci. Instrum. 89, 10F104 (2018)
Descamps, A. et al. An approach for the measurement of the bulk temperature of single crystal diamond using an X-ray free electron laser. Sci. Rep. 10, 14564 (2020).
Wang, X., Scandolo, S. & Car, R. Carbon phase diagram from ab initio molecular dynamics. Phys. Rev. Lett. 95, 185701 (2005).
Correa, A. A., Bonev, S. A. & Galli, G. Carbon under extreme conditions: phase boundaries and electronic properties from first-principles theory. Proc. Natl Acad. Sci. USA 103, 1204–1208 (2006).
Benedict, L. X. et al. Multiphase equation of state for carbon addressing high pressures and temperatures. Phys. Rev. B 89, 224109 (2014).
Zimmerman, G., Kershaw, D., Bailey, D. & Harte, J. LASNEX code for inertial confinement fusion. J. Opt. Soc. Am. 68, 549 (1978).
Boettger, J. C. SESAME Equation Of State For Epoxy. Report LA-12755-MS (Los Alamos National Laboratory, 1994).
Wild, Ch., Herres, N. & Koidl, P. Texture formation in polycrystalline diamond films. J. Appl. Phys. 68, 973–978 (1990).
Vedam, K. & Schmidt, E. D. D. Variation of refractive index of MgO with pressure to 7 kbar. Phys. Rev. 146, 548–554 (1966).
Lazicki, A. et al. X-ray diffraction of solid tin to 1.2 TPa. Phys. Rev. Lett. 115, 075502 (2015).
Acknowledgements
We acknowledge discussions with B. Remington, M. Millot and D. Klug, and we thank the National Ignition Facility staff and the National Ignition Facility Discovery Science programme. This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under contract number DE-AC52-07NA27344. J.S.W. thanks the UK EPSRC for support under grants EP/J017256/1 and EP/S025065/1. D.McG. was supported by LLNS under contract number B595954. Partial funding for G.W.C. and J.R.R. was provided by NSF Physics Frontier Center award PHY-2020249 and DOE NNSA award DE-NA0003856.
Author information
Authors and Affiliations
Contributions
J.S.W. and J.H.E. conceived the work. A.L., D.McG., J.R.R., R.F.S., M.G.G., P.G.H., A.H. and M.J.S. performed the experiments. D.G.B. designed the laser pulse shapes. A.L. analysed the data with assistance from J.R.R., J.H.E., D.E.F., D.E. and J.V.B. D.C.S., F.C., C.E.W., R.G.K., J.M.McN., R.E.R. and G.W.C. contributed to the design of the work and interpretation of the data. A.L. and J.S.W. wrote the paper. All coauthors commented critically on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Philip Dalladay-Simpson and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
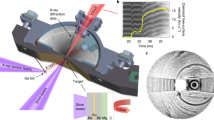
Extended Data Fig. 1 Experimental configuration.
a, Cross-section of diffraction sample: a description of the sample layers for each shot is shown in Extended Data Table 1. b, TARDIS diagnostic geometry with X-ray source (XRS) beam and scattered Bragg peaks on the image plate illustrated by red lines. c, Raw data scans of the three TARDIS image plates for shot N160315.
Extended Data Fig. 2 Summary of reported X-ray diffraction data.
Image plates are background-subtracted and projected into azimuthal angle ϕ versus 2θ and stereographic space. The circular opening at the centre is a hole in the diagnostic through which the VISAR laser can pass. a, N160315 (about 0.8 TPa) has diffraction peaks from the FC8 sample and B2 MgO window. The model ideal diffraction pattern includes the structure factor, multiplicity, Lorentz polarization factor (for a flat powder sample in transmission), and an instrument broadening tuned to match the data (the peak widths are proportional to the spatial extent of the emitting plasma cloud around the X-ray source, which varies somewhat from shot to shot). The peak width FWHM is between 1° and 1.5°, which is consistent with our source size and typical shot-to-shot variation. We do not attempt to model the effects of texture or temperature, which are both important in this data. The high temperatures are primarily responsible for the intensity mismatch between the real and ideal diffraction data at high angle, owing to the Debye–Waller effect. The square-shaped features on the rectangular plate are an array of Ross-pair filters designed to constrain the spectrum of the background radiation. b, N150217 (1.02 TPa): two peaks consistent with the FC8 structure are evident (ideal pattern shown in blue). The large double rectangular feature centred on the VISAR hole (also seen in c and d) is a pinhole image of a region at the front of the TARDIS box that generates fluorescence when illuminated by the hard X-rays and fast electrons coming from the X-ray source. The diagnostic was redesigned after 2015 to eliminate this feature. The smaller rectangular feature centred around the direct beam spot (also seen in c and d) is a combination of fluorescence from the front face of a cylindrical shield positioned around the direct beam spot, to block image plate fluorescence, and the shadow of the fixturing holding the shield in place. The design of this shield was also subsequently improved. c, N150927 (1.18 TPa): in this shot there is evident overlap between the polycrystalline diamond diffraction, which shows up as continuous rings, and strongly textured diffraction from the single-crystal diamond windows. d, N150304 (1.38 TPa). e, N161211 (about 1.8 TPa). In this shot, two spatially and temporally separated X-ray sources were used to yield two separate, easily distinguishable ring patterns, for the purpose of improving image plate calibration (the first pattern is from the undriven target and primarily picks up the scattering from the undriven Au heat shield). On this shot there is also a pattern of Laue spots evident on the image plates because the X-ray source has a broad, high-energy Bremsstrahlung tail that scatters off the windows, which are still undriven single crystals during the earlier X-ray exposure. Laue spots consistent with scattering of 5–25 keV radiation from {001}-oriented single crystal MgO are marked with black squares.
Extended Data Fig. 3 Summary of reported X-ray diffraction data.
a, N170304 (1.74 TPa): two peaks consistent with the FC8 structure are evident. b, N180214 (2.01 TPa): 2–3 peaks consistent with the FC8 structure are evident. The background is so high on this shot that diffraction is observed only when the single-crystal-like texture allows it to arise above the background, as is the case for the (111) peak, or the peak falls in a region of the image plate partially shielded from the ablation plasma background by the pinhole (further explained in Extended Data Fig. 7). This shot used a Zr (16.25 keV) X-ray source to measure diffraction at peak compression (XRS 1), so all peaks appear at lower angles compared to the rest of the shots with Ge (10.25 keV) X-ray sources. The second X-ray source (XRS 2) was Ge, and was fired before the compression wave entered the target, to capture diffraction from uncompressed hexagonal close-packed (hcp) Zr and FC8 diamond. These additional diffraction lines were used to improve the image plate angular calibration. The broadband Bremsstrahlung tail of the Ge X-ray source scattered off the uncompressed single-crystal diamond window to produce the Laue spots, marked with black squares in the stereographic projection. These positions are consistent with scattering from a {110}-oriented crystal, with an energy spanning 15–35 keV.
Extended Data Fig. 4 Laser drive intensities and their relationship to sample stress and image plate background.
a, The sample drive for all but the highest-stress shot N180214 used 16 overlapped beams at the National Ignition Facility with phase plates to produce a 0.9 mm × 1.2 mm elliptical spot when projected onto the sample. The transverse uniformity of the stress in the sample degrades with increasing stress. By 1.8 TPa, two-dimensional radiation-hydrodynamic simulations predict that the uniformity is still within 5% out to a radius of 400 μm but at the highest stress it becomes necessary to delay the lateral release waves by increasing the area of the drive initially. To accomplish this, we tile 8 of the beams to form an approximately uniform 1.8 mm × 1.8 mm square drive spot and use these beams to drive the sample to near 0.8 TPa, after which we drive to 2 TPa using 8 overlapped beams (cartoon inset). With this drive, simulations indicate that the stress is uniform to within 5% out to a radius of 300 μm and drops an additional 2–3% by a radius of 400 μm. The maximum sample radius for which an unobstructed ray may pass through the pinhole aperture is about 330 μm by peak compression (the sample has moved 200 μm closer to the aperture), so this transverse uniformity is adequate. For the highest power laser drives, high background levels on the image plates coming from X-rays produced in the laser-ablation process nearly overwhelm the X-ray diffraction data, and subsequent attempts to measure diffraction above 2 TPa were unsuccessful for that reason. The difficulty of achieving stresses of 2 TPa and higher is illustrated in b. The longitudinal stress produced from a given drive intensity increases in a sublinear fashion, while the increase in background from the ablation plasma is strongly superlinear. Image plate backgrounds shown in this figure were taken from the same regions on the image plate in each shot and were normalized by the relative transmission through the different sample and filter materials and thicknesses.
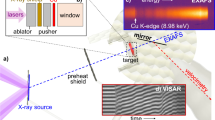
Extended Data Fig. 5 VISAR summary and pressure inference.
a, VISAR velocity histories showing the velocity of the rear surface of the diamond window. In all cases the diamond elastic wave shocks the samples to an initial ~0.1 TPa before subsequent slower compression. By 2 TPa, the elastic wave is nearly overtaken by a strong growing shock that forms within the rear diamond tamper. b, Experimental diamond window free-surface velocity measurement and stress histories in the diamond sample inferred from characteristics analysis, compared to the LASNEX radiation-hydrodynamic code predictions for shot N180214 (2.01 TPa). To achieve reasonable agreement with experimental breakout times and peak velocities, it was necessary in the simulation to turn off diamond strength in the sample and window after the elastic wave had reached the free surface. The characteristics method was also used to infer stress from the LASNEX-predicted free-surface velocity, to demonstrate reasonable agreement with the predicted stress histories. The inferred stress from the characteristics analysis of the LASNEX velocities is systematically slightly lower than the LASNEX stress. We consider this apparent underestimate as an additional systematic contribution to the stress uncertainty.
Extended Data Fig. 6 Steps to subtract the X-ray background on the image plates.
A lineout of the image plate from shot N170305 is shown, for illustration. a, Raw data, projected into ϕ (angle around the direct beam) versus 2θ (scattering angle) space. b, data after the SNIP background subtraction and intensity corrections (which take into account the variable transmission through the sample and image plate filter materials and the changing effective pinhole area depending on the angle of scattered X-rays) are applied. c, Image plate lineouts: the SNIP background (B) is subtracted from the raw data (D), yielding (S). Intensity corrections are then applied, yielding (I). At lower pressures (lower ablation-plasma background) this is often sufficient to flatten the background but when the laser power is very high, an additional polynomial background (P) is subtracted from (I) to generate the final result (R). d shows the diffraction pattern (R, teal line), a fit with Gaussian peak shapes and constant background (black dashed line), and residual (solid black line). The centroids of the Gaussian peaks were used in a least-squares fitting to infer the FC8 density.
Extended Data Fig. 7 Data extraction for shot N180214.
At 2 TPa, the high drive background results in statistical noise levels that almost overwhelm the X-ray diffraction signal, so spurious features in the background show up clearly in the image plate lineouts. Some of the features are highlighted in this image: a pattern of Laue spots which originates from the broadband (modelled as 15–35 keV) Bremsstrahlung tail of the backlighter radiation, scattered off the uncompressed {110}-oriented single-crystal diamond window during the early X-ray source pulse (locations shown in black boxes); a series of bright bands, which are scanning artefacts, are marked with red dashed lines; and an aliasing pattern which arises from low sampling resolution is marked with white dashed lines (the sampling resolution is quite heterogeneous in this projection). As a result of all these spurious features, some diffraction lines that are evident by eye do not rise above the background noise in an average lineout over the entire image plate, and so we have chosen to stitch together narrower lineouts around the apparent diffraction lines. A narrow lineout over a region on the image plate highlighted in blue centred at about −80° is shown as the blue line. A single-crystal-like (111) diffraction line from diamond shows up above the background, because of its strong texture. Based on this texture, the line apparently originates from the single-crystal diamond tamper, which has reached pressure equilibrium with the sample over approximately half its volume by the time of the X-ray exposure. The (200) line and a fragment of the (311) line are largely too weak to register above the background noise from the ablation plasma, but they do show up in some regions of the image plate where the ablation plasma is shielded by the edge of the pinhole aperture, as illustrated by the cartoon inset. The X-rays from the ablation front that comprise the majority of the background are generated further from the pinhole than the Zr Heα X-rays scattered from the sample. There is consequently a narrow region on the image plate where the signal-to-noise ratio of the diffracted X-rays is higher, as shown in the narrow lineout centred near −100° (solid red line). The blue and red lineouts were stitched together, strong spurious features were masked out, and a polynomial background was subtracted, to create the teal-coloured diffraction pattern. The peaks evident by eye were fitted with Gaussian functions and the centroids used in a least-squares fit to infer the density. The residual is shown as the black solid line. The (311) peak position was not used in the least-squares fitting because it is so weak and so limited in azimuthal extent that its existence is questionable.
Extended Data Fig. 8 Ruling out alternate phases.
The observed diffraction peaks easily rule out a high-pressure BC8 or SC1 phase (ideal patterns shown in green and pink, respectively, in a for shot N170209), but the SC4 phase (grey) has peaks that come reasonably close to overlapping those of the FC8 (blue). All model diffraction patterns are plotted at 7.82 g cm−3 SC4 and FC8 peak positions are shown in b. The ‘q1’ diffraction peak angle is several standard deviations away from the expectation for the SC4 phase (shown even more clearly in the plot of the ratio of peak positions q1/q2).
Extended Data Fig. 9 MgO data summary.
VISAR data from shots N160315 (a) and N160519 (b), which used MgO windows. The carbon–MgO interface can be tracked until the compression wave reaches the free surface, although the fringes lose substantial visibility, owing to the B1-to-B2 phase transformation in the MgO window. The ramp equation of state and index of refraction as a function of pressure are not yet well constrained for MgO, so the experimental stress is uncertain. The interface velocity shown here is corrected for the MgO index using an approximate Gladstone–Dale correction of 2.015 from the results of Vedam and Schmidt52. c, Radiation-hydrodynamic simulations of the stress and density histories across the sample for shot N160315. The X-ray source duration is bracketed by dashed white lines. These simulations show that, at the time of the experiment (that is, the duration of the X-ray source), 1/3 to 1/2 of the MgO window is in a uniform stress state at equilibrium with the diamond window, and the remaining volume is experiencing a strong stress gradient in which no single volume will diffract with sufficient intensity. We therefore report the peak positions in d at the same stress as the diamond sample. The pink contours in d show the ideal peak angles for B2 MgO as a function of pressure, taken from the equation of state reported by Coppari et al.29 (data points shown as red triangles) and extrapolated to 2 TPa. The dashed contour, plotted for the B2 (110) peak only, shows the compressibility predicted for the principal adiabat by the Livermore tabulated equation of state model LEOS 219. We also show the peak positions reported to be from the diamond windows in a previous diffraction experiment53 with open black symbols.
Supplementary information
Rights and permissions
About this article
Cite this article
Lazicki, A., McGonegle, D., Rygg, J.R. et al. Metastability of diamond ramp-compressed to 2 terapascals. Nature 589, 532–535 (2021). https://doi.org/10.1038/s41586-020-03140-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-03140-4
This article is cited by
-
Excitonic insulator to superconductor phase transition in ultra-compressed helium
Nature Communications (2023)
-
Materials under extreme conditions using large X-ray facilities
Nature Reviews Methods Primers (2023)
-
Extended X-ray absorption fine structure of dynamically-compressed copper up to 1 terapascal
Nature Communications (2023)
-
Phase transformation path in Aluminum under ramp compression; simulation and experimental study
Scientific Reports (2022)
-
Structure and density of silicon carbide to 1.5 TPa and implications for extrasolar planets
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.