Abstract
Topological crystalline insulators (TCIs) can exhibit unusual, quantized electric phenomena such as fractional electric polarization and boundary-localized fractional charge1,2,3,4,5,6. This quantized fractional charge is the generic observable for identification of TCIs that lack clear spectral features5,6,7, including ones with higher-order topology8,9,10,11. It has been predicted that fractional charges can also manifest where crystallographic defects disrupt the lattice structure of TCIs, potentially providing a bulk probe of crystalline topology10,12,13,14. However, this capability has not yet been confirmed in experiments, given that measurements of charge distributions in TCIs have not been accessible until recently11. Here we experimentally demonstrate that disclination defects can robustly trap fractional charges in TCI metamaterials, and show that this trapped charge can indicate non-trivial, higher-order crystalline topology even in the absence of any spectral signatures. Furthermore, we uncover a connection between the trapped charge and the existence of topological bound states localized at these defects. We test the robustness of these topological features when the protective crystalline symmetry is broken, and find that a single robust bound state can be localized at each disclination alongside the fractional charge. Our results conclusively show that disclination defects in TCIs can strongly trap fractional charges as well as topological bound states, and demonstrate the primacy of fractional charge as a probe of crystalline topology.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the authors on reasonable request.
References
Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 62, 2747–2750 (1989).
Vanderbilt, D. & King-Smith, R. D. Electric polarization as a bulk quantity and its relation to surface charge. Phys. Rev. B 48, 4442–4455 (1993).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654 (1993).
Resta, R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 66, 899–915 (1994).
Hughes, T. L., Prodan, E. & Bernevig, B. A. Inversion-symmetric topological insulators. Phys. Rev. B 83, 245132 (2011).
Turner, A. M., Zhang, Y., Mong, R. S. K. & Vishwanath, A. Quantized response and topology of magnetic insulators with inversion symmetry. Phys. Rev. B 85, 165120 (2012).
van Miert, G. & Ortix, C. Excess charges as a probe of one-dimensional topological crystalline insulating phases. Phys. Rev. B 96, 235130 (2017).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115 (2017).
Benalcazar, W. A., Li, T. & Hughes, T. L. Quantization of fractional corner charge in Cn-symmetric higher-order topological crystalline insulators. Phys. Rev. B 99, 245151 (2019).
Peterson, C. W., Li, T., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A fractional corner anomaly reveals higher-order topology. Science 368, 1114–1118 (2020).
van Miert, G. & Ortix, C. Dislocation charges reveal two-dimensional topological crystalline invariants. Phys. Rev. B 97, 201111 (2018).
Liu, S., Vishwanath, A. & Khalaf, E. Shift insulators: rotation-protected two-dimensional topological crystalline insulators. Phys. Rev. X 9, 031003 (2019).
Li, T., Zhu, P., Benalcazar, W. A. & Hughes, T. L. Fractional disclination charge in two-dimensional Cn-symmetric topological crystalline insulators. Phys. Rev. B 101, 115115 (2020).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Hasan, M. Z. & Kane, C. L. Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).
Teo, J. C. Y., Fu, L. & Kane, C. L. Surface states and topological invariants in three-dimensional topological insulators: application to Bi1−xSbx. Phys. Rev. B 78, 045426 (2008).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Fang, C., Gilbert, M. J. & Bernevig, B. A. Bulk topological invariants in noninteracting point group symmetric insulators. Phys. Rev. B 86, 115112 (2012).
Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017); correction 582, E14 (2020).
Su, W. P., Schrieffer, J. R. & Heeger, A. J. Solitons in polyacetylene. Phys. Rev. Lett. 42, 1698–1701 (1979).
van Miert, G. & Ortix, C. Higher-order topological insulators protected by inversion and rotoinversion symmetries. Phys. Rev. B 98, 081110 (2018).
Teo, J. C. Y. & Hughes, T. L. Existence of Majorana-fermion bound states on disclinations and the classification of topological crystalline superconductors in two dimensions. Phys. Rev. Lett. 111, 047006 (2013).
Benalcazar, W. A., Teo, J. C. Y. & Hughes, T. L. Classification of two-dimensional topological crystalline superconductors and Majorana bound states at disclinations. Phys. Rev. B 89, 224503 (2014).
Grinberg, I. H. et al. Robust temporal pumping in a magneto-mechanical topological insulator. Nat. Commun. 11, 974 (2020).
Bandres, M. A. et al. Topological insulator laser: experiments. Science 359, eaar4005 (2018).
Harari, G. et al. Topological insulator laser: theory. Science 359, eaar4003 (2018).
St-Jean, P. et al. Lasing in topological edge states of a one-dimensional lattice. Nat. Photon. 11, 651–656 (2017).
Hadad, Y., Khanikaev, A. B. & Alù, A. Self-induced topological transitions and edge states supported by nonlinear staggered potentials. Phys. Rev. B 93, 155112 (2016).
Hadad, Y., Soric, J. C., Khanikaev, A. B. & Alù, A. Self-induced topological protection in nonlinear circuit arrays. Nat. Electron. 1, 178–182 (2018).
Zangeneh-Nejad, F. & Fleury, R. Nonlinear second-order topological insulators. Phys. Rev. Lett. 123, 053902 (2019).
Nayak, A. K. et al. Resolving the topological classification of bismuth with topological defects. Sci. Adv. 5, eaax6996 (2019).
Avraham, N. et al. Visualizing coexisting surface states in the weak and crystalline topological insulator Bi2TeI. Nat. Mater. 19, 610–616 (2020).
Martin, J. et al. Localization of fractionally charged quasi-particles. Science 305, 980–983 (2004).
Kastner, M. The single electron transistor and artificial atoms. Ann. Phys. 9, 885–894 (2000).
Mittal, S. et al. Photonic quadrupole topological phases. Nat. Photon. 13, 692–696 (2019).
Liu, S. et al. Topologically protected edge state in two-dimensional Su–Schrieffer–Heeger circuit. Research 2019, 8609875 (2019).
Peterson, C. W., Benalcazar, W. A., Hughes, T. L. & Bahl, G. A quantized microwave quadrupole insulator with topologically protected corner states. Nature 555, 346–350 (2018).
Acknowledgements
The authors thank J. T. Bernhard for access to the resources at the UIUC Electromagnetics Laboratory. This project was supported by the US National Science Foundation (NSF) Emerging Frontiers in Research and Innovation (EFRI) grant EFMA-1641084 and by the US Office of Naval Research (ONR) Multidisciplinary University Research Initiative (MURI) grant N00014-20-1-2325 on Robust Photonic Materials with High-Order Topological Protection. C.W.P. additionally acknowledges support from the NSF Graduate Research Fellowship. G.B. additionally acknowledges support from the ONR Director for Research Early Career Grant N00014-17-1-2209. T.L. and T.L.H. additionally thank the US National Science Foundation under grant DMR-1351895.
Author information
Authors and Affiliations
Contributions
C.W.P. designed and fabricated the microwave circuits, performed the microwave simulations and experimental measurements, and produced the experimental figures. W.J. assisted with the microwave circuit design and experimental measurements. T.L. guided the topological insulator design and performed the theoretical calculations. T.L.H. and G.B. supervised all aspects of the project. All authors jointly wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Carmine Ortix and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
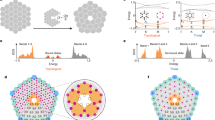
Extended Data Fig. 1 Fractional charge at disclination defects.
a, C4-symmetric HOTI with 1/4 corner charge and 1/2 edge charge. A schematic of the tight-binding model (black dots are atoms, black lines are strong bonds) and illustration of the fractional charge are shown. Owing to its C4 symmetry, the HOTI can be cut into four identical sectors. b, One sector is removed and the remaining three are glued together to create a disclination defect with a negative Frank angle Ω = −90°. Red arrows on the schematic show calculation of the Frank angle. The disclination traps a 3/4 fractional charge, as it is formed by combining three 1/4 charge corners. c, One sector is added and the resulting five are glued together to create a disclination defect with a positive Frank angle Ω = +90°. Red arrows on the schematic show calculation of the Frank angle. The disclination traps a 1/4 fractional charge, as it is formed by combining five 1/4 charge corners. d, Photo of fabricated microwave-frequency circuit topological insulator with disclination having a Frank angle Ω = −90°. e, Photo of fabricated circuit with disclination having a Frank angle Ω = +90°. Insets show C4-symmetric bulk coupling.
Extended Data Fig. 2 Burgers vector and Frank angle of disclinations.
a, b, Demonstration of calculating the Burgers vector and Frank angle for a C4-symmetric square lattice with the type-I disclination (a) and type-II disclination (b). The black arrows indicate the vector being parallel transport enclosing the disclination core and the dashed grey arrows indicate that vector in the process of the parallel transport. c, d, The Wannier centre configuration and fractional charge in defective lattices with the type-I disclination (c) and type-I disclination (d). e, Allowed positions of Wannier centres by the C4 symmetry in one unit cell.
Extended Data Fig. 3 Spectral flow of topological bound states.
a, Schematic of the lattice configuration for the C3 symmetric TCI. t0 and t indicate the intracell coupling strength and intercell coupling strength, respectively. We apply an on-site potential to the bottom-left corner site. b, The spectrum of the C3 TCI as a function of on-site potential α for a topological phase with t = 1.0 and t0 = 0.5 (top) and a trivial phase with t = 0.5 and t = 1.0 (bottom). The red line represents energy shift of the corner mode. c, The spatial distribution of the in-gap mode (encircled in b) over the bottom-left corner of the lattice. We use α = −1 for the topological phase and α = 1 for the trivial phase. The simulation is conducted on a triangle lattice with 15 unit cells per side.
Extended Data Fig. 4 Removing lattice sites.
a, d, Lattice configuration of the HOTI used in simulations. We consider a lattice with 10 × 10 unit cells, intracell coupling strength of 0.25 (dashed lines) and intercell coupling strength of 1 (solid lines). The resonator being removed is denoted by a red circle. b, e, The spectrum of the lattice in a and d as a function of the on-site potential applied to the highlighted resonators. c, f, The fractional part of the mode density integrated over the shaded sector in a and d for each band.
Extended Data Fig. 5 Fractional mode density in large systems.
Tight-binding simulation of fractional mode density in large systems (15 unit cells per side) with Frank angles Ω = ±90°. We set the intercell coupling strength to be 1 and intracell coupling strength to be 0.2. a, Simulated DOS spectrum and real-space distribution of in-gap modes for a Frank angle Ω = −90°. On-site potentials are applied to the corner sites to pull the corner states into the bulk bandgap. b, Fractional portion of the mode density for each band. The colour of each unit cell indicates the fractional portion of mode density in that cell, and the area of each dot is proportional to the mode density of the corresponding resonator. The fractional part of the integrated mode density around the central unit cell is 3/4 for bands 1 and 3 and 1/2 for band 2. c, d, Same as a and b but for Frank angle Ω = +90°. The fractional part of the integrated mode density around the central unit cell is 1/4 for bands 1 and 3 and 1/2 for band 2.
Extended Data Fig. 6 Fractional mode density in large trivial and deformed systems.
a, b, Tight-binding simulation of fractional mode density in large topologically trivial system (15 unit cells per side) with a Frank angle Ω = −90°. We set the intercell coupling strength to be 0.2 and intracell coupling strength to be 1. a, Simulated DOS spectrum and real-space distribution of in-gap modes. The in-gap modes are localized within the central defective unit cell, which only has three sites. b, Fractional portion of the mode density for each band. The mode density takes an integer value in all unit cells. c–e, Tight-binding simulation of fractional mode density in a large system (15 unit cells per side) with a Frank angle Ω = −90° and with the central unit cell trivialized. We set the intercell coupling strength to be 1 and intracell coupling strength to be 0.2. c, Schematic of deformed lattice with trivialized central unit cell. d, Simulated DOS spectrum and real-space distribution of in-gap modes. On-site potentials are applied to the corner sites as well as the ‘interior corners’ to pull six topological bound states into the bulk bandgap. e, Fractional portion of the mode density for each band. The colour of each unit cell indicates the fractional portion of mode density in that cell, and the area of each dot is proportional to the mode density of the corresponding resonator. The fractional part of the integrated mode density around the central unit cell remains 3/4 for bands 1 and 3 and 1/2 for band 2.
Extended Data Fig. 7 Detailed mode density for the C3-symmetric insulator.
Measured mode density for the C3-symmetric insulator, as shown in Fig. 1c. The total mode density for each band is listed numerically in each unit cell, and the area of each dot is proportional to the mode density of the corresponding resonator. The colour of each unit cell indicates the fractional portion of mode density.
Extended Data Fig. 8 Detailed mode density for the C5-symmetric insulator.
Measured mode density for the C5-symmetric insulator, as shown in Fig. 1d. The total mode density for each band is listed numerically in each unit cell, and the area of each dot is proportional to the mode density of the corresponding resonator. The colour of each unit cell indicates the fractional portion of mode density.
Extended Data Fig. 9 Detailed mode density for deformed C3-symmetric insulator.
a, Measured fractional mode density for the C3-symmetric insulator after the central unit cell is trivialized, as shown in Fig. 2c. The total mode density for each band is listed numerically in each unit cell, and the area of each dot is proportional to the mode density of the corresponding resonator. The colour of each unit cell indicates the fractional portion of mode density. b, Same as a but with broken rotation symmetry as in Fig. 2f.
Extended Data Fig. 10 Detailed mode density for deformed C5-symmetric insulator.
a, Measured fractional mode density for the C5-symmetric insulator after the central unit cell is trivialized, as shown in Fig. 3c. The total mode density for each band is listed numerically in each unit cell, and the area of each dot is proportional to the mode density of the corresponding resonator. The colour of each unit cell indicates the fractional portion of mode density. b, Same as a but with broken rotation symmetry as in Fig. 3f.
Rights and permissions
About this article
Cite this article
Peterson, C.W., Li, T., Jiang, W. et al. Trapped fractional charges at bulk defects in topological insulators. Nature 589, 376–380 (2021). https://doi.org/10.1038/s41586-020-03117-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-03117-3
This article is cited by
-
Vortex nanolaser based on a photonic disclination cavity
Nature Photonics (2024)
-
Transport measurement of fractional charges in topological models
npj Quantum Materials (2023)
-
Observation of nonlinear disclination states
Light: Science & Applications (2023)
-
Topological phenomena at defects in acoustic, photonic and solid-state lattices
Nature Reviews Physics (2023)
-
A second wave of topological phenomena in photonics and acoustics
Nature (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.