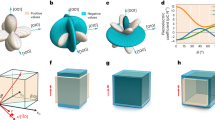
Abstract
Transparent piezoelectrics are highly desirable for numerous hybrid ultrasound–optical devices ranging from photoacoustic imaging transducers to transparent actuators for haptic applications1,2,3,4,5,6,7. However, it is challenging to achieve high piezoelectricity and perfect transparency simultaneously because most high-performance piezoelectrics are ferroelectrics that contain high-density light-scattering domain walls. Here, through a combination of phase-field simulations and experiments, we demonstrate a relatively simple method of using an alternating-current electric field to engineer the domain structures of originally opaque rhombohedral Pb(Mg1/3Nb2/3)O3-PbTiO3 (PMN-PT) crystals to simultaneously generate near-perfect transparency, an ultrahigh piezoelectric coefficient d33 (greater than 2,100 picocoulombs per newton), an excellent electromechanical coupling factor k33 (about 94 per cent) and a large electro-optical coefficient γ33 (approximately 220 picometres per volt), which is far beyond the performance of the commonly used transparent ferroelectric crystal LiNbO3. We find that increasing the domain size leads to a higher d33 value for the [001]-oriented rhombohedral PMN-PT crystals, challenging the conventional wisdom that decreasing the domain size always results in higher piezoelectricity8,9,10. This work presents a paradigm for achieving high transparency and piezoelectricity by ferroelectric domain engineering, and we expect the transparent ferroelectric crystals reported here to provide a route to a wide range of hybrid device applications, such as medical imaging, self-energy-harvesting touch screens and invisible robotic devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available on request from the corresponding authors.
References
Wang, L. V. Multiscale photoacoustic microscopy and computed tomography. Nat. Photon. 3, 503–509 (2009).
Chen, X. et al. Transparent lead lanthanum zirconate titanate (PLZT) ceramic fibers for high-frequency ultrasonic transducer applications. Ceram. Int. 42, 18554–18559 (2016).
Tshering, C. & Tshering, D. Renewable mobile charger using piezoelectric transducer. Res. J. Recent Sci. 7, 20–23 (2018).
Sette, D. et al. Transparent piezoelectric transducers for large area ultrasonic actuators. In 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS). 793–796 (IEEE, 2017).
Modarres, A., Ramstein, C., Cruz-Hernandez, J. M., Danny, A. & Grant, A. G. Transparent composite piezoelectric combined touch sensor and haptic actuator. US Patent 2011/0261021 A1 (2011).
Thalhammer, G., McDougall, C., MacDonald, M. P. & Ritsch-Marte, M. Acoustic force mapping in a hybrid acoustic-optical micromanipulation device supporting high resolution optical imaging. Lab Chip 16, 1523–1532 (2016).
Niederhauser, J. J., Jaeger, M., Hejazi, M., Keppner, H. & Frenz, M. Transparent ITO coasted PVDF transducer for optoacoustic depth profiling. Opt. Commun. 253, 401–406 (2005).
Wada, S., Yako, K., Kakemoto, H., Tsurumi, T. & Kiguchi, T. Enhanced piezoelectric properties of barium titanate single crystals with different engineered-domain sizes. J. Appl. Phys. 98, 014109 (2005).
Hlinka, J., Ondrejkovic, P. & Marton, P. The piezoelectric response of nanotwinned BaTiO3. Nanotechnology 20, 105709 (2009).
Ahluwalia, R., Lookman, T., Saxena, A. & Cao, W. Domain-size dependence of piezoelectric properties of ferroelectrics. Phys. Rev. B 72, 014112 (2005).
Jaffe, B., Cook, W. R. & Jaffe, H. Piezoelectric Ceramics (Academic, 1971).
Damjanovic, D. Comments on origins of enhanced piezoelectric properties in ferroelectrics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56, 1574–1585 (2009).
Sun, E. W. & Cao, W. W. Relaxor-based ferroelectric single crystals: growth, domain engineering, characterization and applications. Prog. Mater. Sci. 65, 124–210 (2014).
Zhang, S. J. et al. Advantages and challenges of relaxor-PT ferroelectric crystals for electroacoustic transducers—a review. Prog. Mater. Sci. 68, 1–66 (2015).
Haertling, G. H. Ferroelectric ceramics: history and technology. J. Am. Ceram. Soc. 82, 797–818 (1999).
Ruan, W. et al. Large electro-optic effect in La-doped 0.75Pb(Mg1/3Nb2/3)O3-0.25PbTiO3 transparent ceramic by two-stage sintering. J. Am. Ceram. Soc. 93, 2128–2131 (2010).
Glazer, A. M., Lewis, J. G. & Kaminsky, W. An automatic optical imaging system for birefringent media. Proc. R. Soc. Lond. A 452, 2751–2765 (1996).
Shvartsman, V. & Kholkin, A. Domain structure of 0.8Pb(Mg1/3Nb2/3)O3-0.2PbTiO3 studied by piezoresponse force microscopy. Phys. Rev. B 69, 014102 (2004).
Bai, F., Li, J. & Viehland, D. Domain hierarchy in annealed (001)-oriented Pb (Mg1/3Nb2/3)O3-x% PbTiO3 single crystals. Appl. Phys. Lett. 85, 2313–2315 (2004).
Sato, Y., Hirayama, T. & Ikuhara, Y. Real-time direct observations of polarization reversal in a piezoelectric crystal: Pb(Mg1/3Nb2/3)O3-PbTiO3 studied via in situ electrical biasing transmission electron microscopy. Phys. Rev. Lett. 107, 187601 (2011).
Kleemann, W. Relaxor ferroelectrics: cluster glass ground state via random fields and random bonds. Phys. Stat. Sol. B 251, 1993–2002 (2014).
Bokov, A. A. & Ye, Z. G. Recent progress in relaxor ferroelectrics with perovskite structure. J. Mater. Sci. 41, 31–52 (2006).
Krogstad, M. J. et al. The relation of local order to material properties in relaxor ferroelectrics. Nat. Mater. 17, 718–724 (2018).
Takenaka, H., Grinberg, I., Liu, S. & Rappe, A. M. Slush-like polar structures in single-crystal relaxors. Nature 546, 391–395 (2017).
Wan, X. M., Luo, H. S., Wang, J., Chan, H. L. W. & Choy, C. L. Investigation on optical transmission spectra of (1–x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 single crystals. Solid State Commun. 129, 401–405 (2004).
Wemple, S. Polarization fluctuations and the optical-absorption edge in BaTiO3. Phys. Rev. B 2, 2679–2689 (1970).
Ogawa, T., Matsushita, M. & Tachi, Y. Domain controlled piezoelectric single crystal and fabrication method therefor. US Patent 2003/0178914 A1 (2003).
Yamashita, Y., Yamamoto, N., Hosono, Y. & Itsumi, K. Piezoelectric transducer, ultrasonic probe, and piezoelectric transducer manufacturing method. US Patent 2015/0372219 A1 (2015).
Chang, W. Y. et al. Dielectric and piezoelectric properties of 0.7Pb(Mg1/3Nb2/3)O3-0.3PbTiO3 single crystal poled using alternating current. Mater. Res. Lett. 6, 537–544 (2018).
Xu, J. et al. Piezoelectric performance enhancement of Pb(Mg1/3Nb2/3)O3-0.25PbTiO3 crystals by alternating current polarization for ultrasonic transducer. Appl. Phys. Lett. 112, 182901 (2018).
Budimir, M., Damjanovic, D. & Setter, N. Piezoelectric response and free-energy instability in the perovskite crystals BaTiO3, PbTiO3, and Pb(Zr,Ti)O3. Phys. Rev. B 73, 174106 (2006).
Sluka, T., Tagantsev, A. K., Damjanovic, D., Gureev, M. & Setter, N. Enhanced electromechanical response of ferroelectrics due to charged domain walls. Nat. Commun. 3, 748 (2012).
Xiang, Y., Zhang, R. & Cao, W. Optimization of piezoelectric properties for [001]c poled 0.94 Pb (Zn1/3Nb2/3)O3–0.06 PbTiO3 single crystals. Appl. Phys. Lett. 96, 092902 (2010).
Li, F. et al. Transparent ferroelectric crystals with ultrahigh piezoelectricity. Provisional US Patent 16/541,309 (2019).
Li, F., Wang, L., Jin, L., Xu, Z. & Zhang, S. J. Achieving single domain relaxor-PT crystals by high temperature poling. CrystEngComm 16, 2892–2897 (2014).
Wan, X. M., Chan, H. L. W., Choy, C. L., Zhao, X. & Luo, H. Optical properties of (1–x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 single crystals studied by spectroscopic ellipsometry. J. Appl. Phys. 96, 1387–1391 (2004).
Wan, X. M. et al. Refractive indices and linear electro-optic properties of (1–x)Pb(Mg1/3Nb2/3)O3-xPbTiO3 single crystals. Appl. Phys. Lett. 85, 5233–5235 (2004).
Wang, J., Shi, S. Q., Chen, L.-Q., Li, Y. & Zhang, T. Y. Phase-field simulations of ferroelectric/ferroelastic polarization switching. Acta Mater. 52, 749–764 (2004).
Wang, J., Wang, B. & Chen, L.-Q., Understanding, predicting, and designing ferroelectric domain structures and switching guided by the phase-field method. Annu. Rev. Mater. Res. 49, 127–152 (2019).
Khakpash, N., Khassaf, H., Rossetti, G. A. Jr & Alpay, S. P. Misfit strain phase diagrams of epitaxial PMN-PT films. Appl. Phys. Lett. 106, 082905 (2015).
Li, F., Jin, L., Xu, Z., Wang, D. & Zhang, S. J. Electrostrictive effect in Pb(Mg1/3Nb2/3)O3-x PbTiO3 crystals. Appl. Phys. Lett. 102, 152910 (2013).
Li, F. et al. The origin of ultrahigh piezoelectricity in relaxor-ferroelectric solid solution crystals. Nat. Commun. 7, 13807 (2016).
Towns, J. et al. XSEDE: accelerating scientific discovery. Comput. Sci. Eng. 16, 62–74 (2014).
Nystrom, N. A., Levine, M. J., Roskies, R. Z. & Scott, J. R. Bridges: a uniquely flexible HPC resource for new communities and data analytics. In Proc. 2015 Annual Conference on Extreme Science and Engineering Discovery Environment (ACM, 2015); https://doi.org/10.1145/2792745.2792775.
Acknowledgements
F.L. and Z.X. acknowledge the support of the National Natural Science Foundation of China (grant numbers 51922083, 51831010 and 51761145024), the development programme of Shaanxi province (grant number 2019ZDLGY04-09) and the 111 Project (B14040). B.W. and L.Q.C. acknowledge the support of the US National Science Foundation under the grant number DMR-1744213 and Materials Research Science and Engineering Center (MRSEC) grant number DMR-1420620. N.Z. thanks the NSFC for support under grant number 1604123. The computer simulations were performed on the ICS-ACI Computing Systems at Pennsylvania State University through the Penn State Institute for Cyber Science and at the Extreme Science and Engineering Discovery Environment cluster supported by National Science Foundation grant number ACI-1548562; the Bridges system was used, which is supported by NSF award number ACI-1445606 at the Pittsburgh Supercomputing Centre under the allocation DMR170006. S.Z. thanks the ONRG (grant number N62909-18-12168) and ARC (grant number FT140100698) for support. T.R.S. was supported by the US ONR.
Author information
Authors and Affiliations
Contributions
The work was conceived and designed by S.Z., L.Q.C. and F.L. C.Q. performed the piezoelectric and optical experiments. F.L. and Z.X. supervised the piezoelectric and dielectric measurements. N.Z. and F.L. supervised the optical experiments. B.W. performed the phase-field simulations and discussed with F.L. L.Q.C. supervised the simulation work. J.L. assisted with the piezoelectric measurements. N.Z. and D.W. performed XRD experiments. Y.W. and H.T. assisted with the optical measurements. F.L. drafted the manuscript, S.Z., N.Z., L.Q.C. and T.R.S. revised the manuscript and all authors discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Wook Jo and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
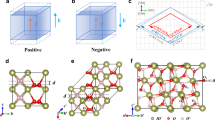
Extended Data Fig. 1 Schematic diagrams of the projections of optical indicatrices on both sides of a domain wall.
a, 109° domain wall; b, 71° domain wall. The prerequisite for the light scattering and reflection at an interface is the difference in refractive indices between the optical media on each side of the interface. As shown here, the principal axes of the optical indicatrix projected on the (001) plane are the same for domains on each side of a 109° domain wall. Thus, no and ne do not change as the light crosses a 109° domain wall, resulting in the absence of light scattering and/or reflection. In contrast, the principal axis of the optical indicatrix projected on the (001) plane rotates by 90° as the light travels across a 71° domain wall, resulting in the alternating of refractive indices no and ne. This is the reason that 71° domain walls scatter and/or reflect the light.
Extended Data Fig. 2 The variation in various energies of PMN-28PT during the first four cycles of a.c. poling.
The data are obtained by phase-field simulations. Here we plot the normalized energies, which are dimensionless.
Extended Data Fig. 3 Effects of system size and mechanical boundary conditions on the a.c.- and d.c.-poled domain structures from phase-field simulations.
a, Effects of system size (at the clamped boundary condition). b, Effects of the mechanical boundary condition (the scale of the simulation is 512 × 512 nm).
Extended Data Fig. 4 Characterization of the domain size along the poling direction for [001]-oriented rhombohedral PMN–PT crystals.
a, PLM images on the (100) face for [001]-poled PMN-28PT crystals under a.c. poling. b, PLM images on the (100) face for [001]-poled PMN-28PT crystals under d.c. poling. c, Distribution of the thickness of laminar domains for the a.c.-poled sample measured from a. d, Distribution of the thickness of laminar domains for the d.c.-poled sample measured from b. The thickness of the samples is around 100 μm. As shown in this figure, no clear difference is observed for the thickness of laminar domains between a.c.- and d.c.-poled samples.
Extended Data Fig. 5 Pseudo-Voight fittings of the {222} diffraction peaks at high-2θ.
a,b, The unpoled sample. c,d, The d.c.-poled sample. e,f, The a.c.-poled sample. a,c,e, The intensity of the patterns accumulated along Ω. b,d,f, The intensity of the patterns accumulated along 2θ.
Extended Data Fig. 6
Effective light absorption coefficients of a.c.- and d.c.-poled PMN-28PT crystals.
Extended Data Fig. 7 The temperature stability of a.c.- and d.c.-poled PMN-28PT crystals.
a, d33, ε33T/ε0 and k33 as a function of temperature. The dwelling time for each testing temperature is 10 min. b, Domain structure of a.c.-poled PMN-28PT crystals as a function of temperature. The temperature is increased from 25 to 100 °C at a rate of 1 °C min−1. The dwelling time for each testing temperature is 30 min.
Extended Data Fig. 8 PLM images of [001]-oriented PMN-28PT crystals with different poling conditions.
a–d, Images obtained from the crystals poled by an a.c. electric field at frequencies of 0.1 Hz (a), 1 Hz (b), 10 Hz (c) and 100 Hz (d), respectively. e, f, Enlargements of the regions in b and c, respectively. g–i, Images obtained from the crystals poled by a d.c. electric field. g, i, Magnifications of the two regions circled in h. The thickness of the samples is 0.5 mm. There are numerous cross-like domain walls in d.c.-poled samples, whereas these types of domain wall are removed by an a.c. electric field.
Extended Data Fig. 9 Dielectric permittivity and piezoelectric coefficient of the a.c.-poled PMN-28PT crystal as a function of the cycle number and frequency.
a, Dielectric permittivity as a function of the cycle number. b, Dielectric permittivity as a function of the frequency. c, Piezoelectric coefficient as a function of the frequency. Five samples are used for each frequency. The error bars indicate the s.d. of the corresponding data.
Supplementary information
Video 1
Domain evolution of the [001]-oriented PMN-28PT crystal during AC-poling. This is a video obtained from a phase-field simulation of domain evolution under an AC electric field. In the video, the colours represent ferroelectric domains with different polarization directions as illustrated in Fig. 1 of the main text.
Video 2
Domain evolution of the [001]-oriented PMN-28PT crystal during the reversal of the polarity of electric field. This video presents the domain evolution of an enlarged local region in supplementary video 1.
Video 3
Domain evolution of the [001]-oriented PMN-28PT crystal during DC-poling. This is a video obtained from a phase-field simulation of domain evolution under a DC electric field. In the video, the colours represent ferroelectric domains with different polar directions as illustrated in Fig. 1 of the main text.
Rights and permissions
About this article
Cite this article
Qiu, C., Wang, B., Zhang, N. et al. Transparent ferroelectric crystals with ultrahigh piezoelectricity. Nature 577, 350–354 (2020). https://doi.org/10.1038/s41586-019-1891-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1891-y
This article is cited by
-
Multiscale reconfiguration induced highly saturated poling in lead-free piezoceramics for giant energy conversion
Nature Communications (2024)
-
Tunable and parabolic piezoelectricity in hafnia under epitaxial strain
Nature Communications (2024)
-
Designing transparent piezoelectric metasurfaces for adaptive optics
Nature Communications (2024)
-
Tuning ferroelectric phase transition temperature by enantiomer fraction
Nature Communications (2024)
-
Structural, linear and nonlinear optical properties of Pb(Mg1/3Nb2/3)O3-PbTiO3 nanoparticles
Chemical Papers (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.