Abstract
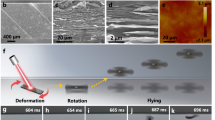
Flying insects capable of navigating in highly cluttered natural environments can withstand in-flight collisions because of the combination of their low inertia1 and the resilience of their wings2, exoskeletons1 and muscles. Current insect-scale (less than ten centimetres long and weighing less than five grams) aerial robots3,4,5,6 use rigid microscale actuators, which are typically fragile under external impact. Biomimetic artificial muscles7,8,9,10 that are capable of large deformation offer a promising alternative for actuation because they can endure the stresses caused by such impacts. However, existing soft actuators11,12,13 have not yet demonstrated sufficient power density to achieve lift-off, and their actuation nonlinearity and limited bandwidth create further challenges for achieving closed-loop (driven by an input control signal that is adjusted based on sensory feedback) flight control. Here we develop heavier-than-air aerial robots powered by soft artificial muscles that demonstrate open-loop (driven by a predetermined signal without feedback), passively stable (upright during flight) ascending flight as well as closed-loop, hovering flight. The robots are driven by multi-layered dielectric elastomer actuators that weigh 100 milligrams each and have a resonance frequency of 500 hertz and power density of 600 watts per kilogram. To increase the mechanical power output of the actuator and to demonstrate flight control, we present ways to overcome challenges unique to soft actuators, such as nonlinear transduction and dynamic buckling. These robots can sense and withstand collisions with surrounding obstacles and can recover from in-flight collisions by exploiting material robustness and vehicle passive stability. We also fly two micro-aerial vehicles simultaneously in a cluttered environment. They collide with the wall and each other without suffering damage. These robots rely on offboard amplifiers and an external motion-capture system to provide power to the dielectric elastomer actuators and to control their flight. Our work demonstrates how soft actuators can achieve sufficient power density and bandwidth to enable controlled flight, illustrating the potential of developing next-generation agile soft robots.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data generated or analysed for this paper are included in the published article, its Methods, and its Supplementary Information. Original videos, computer code and sensor data are available from the corresponding author on reasonable request.
References
Dickerson, A. K., Shankles, P. G., Madhavan, N. M. & Hu, D. L. Mosquitoes survive raindrop collisions by virtue of their low mass. Proc. Natl Acad. Sci. USA 109, 9822–9827 (2012).
Mountcastle, A. M. & Combes, S. A. Biomechanical strategies for mitigating collision damage in insect wings: structural design versus embedded elastic materials. J. Exp. Biol. 217, 1108–1115 (2014).
Ma, K. Y., Chirarattananon, P., Fuller, S. B. & Wood, R. J. Controlled flight of a biologically inspired, insect-scale robot. Science 340, 603–607 (2013).
Chen, Y. et al. A biologically inspired, flapping-wing, hybrid aerial-aquatic microrobot. Sci. Robot. 2, eaao5619 (2017).
Zou, Y., Zhang, W. & Zhang, Z. Liftoff of an electromagnetically driven insect-inspired flapping-wing robot. IEEE Trans. Robot. 32, 1285–1289 (2016).
de Croon, G. C. H. E., De Clercq, K. M. E., Ruijsink, R., Remes, B. & De Wagter, C. Design, aerodynamics, and vision-based control of the DelFly. Int. J. Micro Air Veh. 1, 71–97 (2009).
Carpi, F., Bauer, S. & Rossi, D. D. Stretching dielectric elastomer performance. Science 330, 1759–1761 (2010).
Rosset, S. & Shea, H. R. Flexible and stretchable electrodes for dielectric elastomer actuators. Appl. Phys. A 110, 281–307 (2013).
Zhao, H. et al. Compact dielectric elastomer linear actuators. Adv. Funct. Mater. 28, 1804328 (2018).
Acome, E. et al. Hydraulically amplified self-healing electrostatic actuators with muscle-like performance. Science 359, 61–65 (2018).
Pelrine, R. et al. Dielectric elastomer artificial muscle actuators: toward biomimetic motion. In Smart Structures and Materials 2002: Electroactive Polymer Actuators And Devices (EAPAD) Vol. 4695, 126–137 (International Society for Optics and Photonics, 2002); https://www.spiedigitallibrary.org/conference-proceedings-of-spie/4695/0000/Dielectric-elastomer-artificial-muscle-actuators-toward-biomimetic-motion/10.1117/12.475157.full.
Zhao, J., Niu, J., McCoul, D., Leng, J. & Pei, Q. A rotary joint for a flapping wing actuated by dielectric elastomers: design and experiment. Meccanica 50, 2815–2824 (2015).
Lau, G.-K., Lim, H.-T., Teo, J.-Y. & Chin, Y.-W. Lightweight mechanical amplifiers for rolled dielectric elastomer actuators and their integration with bio-inspired wing flappers. Smart Mater. Struct. 23, 025021 (2014).
Shepherd, R. F. et al. Multigait soft robot. Proc. Natl Acad. Sci. USA 108, 20400–20403 (2011).
Rus, D. & Tolley, M. T. Design, fabrication and control of soft robots. Nature 521, 467–475 (2015).
Majidi, C. Soft robotics: a perspective—current trends and prospects for the future. Soft Robot. 1, 5–11 (2014).
Choe, K. et al. Performance characteristics of electro-chemically driven polyacrylonitrile fiber bundle actuators. J. Intell. Mater. Syst. Struct. 17, 563–576 (2006).
Suzumori, K., Iikura, S. & Tanaka, H. Applying a flexible microactuator to robotic mechanisms. IEEE Contr. Syst. Mag. 12, 21–27 (1992).
Onal, C. D., Chen, X., Whitesides, G. M. & Rus, D. Soft mobile robots with on-board chemical pressure generation. In Robotics Research 525–540 (Springer, 2017).
Katzschmann, R. K., Marchese, A. D. & Rus, D. Hydraulic autonomous soft robotic fish for 3D swimming. In Experimental Robotics 405–420 (Springer, 2016).
Loomis, J., Xu, P. & Panchapakesan, B. Stimuli-responsive transformation in carbon nanotube/expanding microsphere–polymer composites. Nanotechnology 24, 185703 (2013).
Cheng, N. G., Gopinath, A., Wang, L., Iagnemma, K. & Hosoi, A. E. Thermally tunable, self-healing composites for soft robotic applications. Macromol. Mater. Eng. 299, 1279–1284 (2014).
Sadeghipour, K., Salomon, R. & Neogi, S. Development of a novel electrochemically active membrane and ‘smart’ material based vibration sensor/damper. Smart Mater. Struct. 1, 172 (1992).
Pei, Q., Rosenthal, M., Stanford, S., Prahlad, H. & Pelrine, R. Multiple-degrees-of-freedom electroelastomer roll actuators. Smart Mater. Struct. 13, N86 (2004).
Shian, S., Bertoldi, K. & Clarke, D. R. Use of aligned fibers to enhance the performance of dielectric elastomer inchworm robots. In Electroactive Polymer Actuators and Devices (EAPAD) 94301P (International Society for Optics and Photonics, 2015); https://www.spiedigitallibrary.org/conference-proceedings-of-spie/9430/94301P/Use-of-aligned-fibers-to-enhance-the-performance-of-dielectric/10.1117/12.2084140.full.
Li, T. et al. Fast-moving soft electronic fish. Sci. Adv. 3, e1602045 (2017).
Berlinger, F. et al. A modular dielectric elastomer actuator to drive miniature autonomous underwater vehicles. In IEEE Int. Conf. on Robotics and Automation (ICRA). 3429–3435 (IEEE, 2018).
Dickinson, M. H. Muscle efficiency and elastic storage in the flight motor of Drosophila. Science 268, 87–90 (1995).
Chen, Y., Gravish, N., Desbiens, A. L., Malka, R. & Wood, R. J. Experimental and computational studies of the aerodynamic performance of a flapping and passively rotating insect wing. J. Fluid Mech. 791, 1–33 (2016).
Tu, Z., Fei, F., Zhang, J. & Deng, X. Acting is seeing: navigating tight space using flapping wings. Preprint at https://arxiv.org/abs/1902.08688 (2019).
Jayaram, K., Jafferis, N. T., Doshi, N., Goldberg, B. & Wood, R. J. Concomitant sensing and actuation for piezoelectric microrobots. Smart Mater. Struct. 27, 065028 (2018).
Jafferis, N. T., Helbling, E. F., Karpelson, M. & Wood, R. J. Untethered flight of an insect-sized flapping-wing microscale aerial vehicle. Nature 570, 491–495 (2019).
Kellaris, N., Venkata, V. G., Smith, G. M., Mitchell, S. K. & Keplinger, C. Peano-HASEL actuators: muscle-mimetic, electrohydraulic transducers that linearly contract on activation. Sci. Robot. 3, eaar3276 (2018).
Whitney, J. P. & Wood, R. J. Conceptual design of flapping-wing micro air vehicles. Bioinspir. Biomim. 7, 036001 (2012).
Whitney, J. P., Sreetharan, P. S., Ma, K. Y. & Wood, R. J. Pop-up book MEMS. J. Micromech. Microeng. 21, 115021 (2011).
Chen, Y., Ma, K. & Wood, R. J. Influence of wing morphological and inertial parameters on flapping flight performance. In IEEE/RSJ Int. Conf. on Intelligent Robots and Systems 2329–2336 (IEEE, 2016).
Liang, J. et al. Intrinsically stretchable and transparent thin-film transistors based on printable silver nanowires, carbon nanotubes and an elastomeric dielectric. Nat. Commun. 6, 7647 (2015).
Keplinger, C. et al. Stretchable, transparent, ionic conductors. Science 341, 984–987 (2013).
Vatankhah-Varnoosfaderani, M. et al. Bottlebrush elastomers: a new platform for freestanding electroactuation. Adv. Mater. 29, 1604209 (2017).
Kellaris, N., Venkata, V. G., Rothemund, P. & Keplinger, C. An analytical model for the design of Peano-HASEL actuators with drastically improved performance. Extreme Mech. Lett. 29, 100449 (2019).
Acknowledgements
We thank Y. Zhu for comments and discussion. This work is supported by the National Science Foundation (award number CMMI-1830291) and the Wyss Institute for Biologically Inspired Engineering. In addition, the prototypes were enabled by equipment supported by the Army Research Office DURIP programme (award number W911NF-13-1-0311). Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Contributions
Y.C., H.Z., and R.J.W. proposed and designed the research. Y.C., H.Z. and J.M. built the robot. Y.C., H.Z., J.M., P.C. and E.F.H. conducted the experimental work. Y.C., H.Z., P.C., N.-s.P.H., D.R.C. and R.J.W. contributed to modelling and data analysis. Y.C. wrote the paper. All authors provided feedback.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Dario Floreano, Christoph Keplinger and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Design and fabrication of robot components.
a, A 40-mg airframe made of eight pieces of carbon fibre composites. Scale bar represents 2 mm. b, Top view of the planar four-bar transmission. The red arrow marks l3, which is the inverse of the transmission ratio T. Scale bar represents 200 μm. c, Front view of the wing hinge. The hinge width (hw), length (hl), and thickness (ht) determine its torsional stiffness. Scale bar represents 1 mm. d, Front view of a robot wing whose wing span (R) and centre of pressure (rcp) are 10 mm and 7 mm, respectively. Scale bar represents 2 mm. e, An illustration of rolling an elastomer-electrode multilayer into a DEA. f, A zoomed-in illustration of the inset shown in e. g, A zoomed-in illustration of the inset shown in f. The bottom layer of the top multi-layer and the top layer of the bottom multi-layer forms a region that can be actuated. h, Confocal microscopy image of the DEA’s cross section. The elastomer sheet is 220 μm thick and it has seven elastomer layers. The thickness of the top and the bottom layers are approximately 65% of the middle layers. Scale bar represents 100 μm. i, Fabrication of the DEA. After the elastomer sheet is rolled into a cylindrical shell, the top and bottom cap are glued onto the DEA. A weight is placed on top of the DEA as the glue cures. After the glue cures, the DEA connections remain in compression (red) while the rest of the DEA returns to its neutral state (green). j, Front view of a DEA. Scale bar represents 3 mm.
Extended Data Fig. 2 Characterization of blocked force, free displacement and power dissipation.
a, Experimental setup for measuring the DEA’s blocked force. b, Experimental setup for measuring the DEA’s free displacement. c, d, Sample blocked force (c) and free displacement (d) measurements when the DEA is driven at 350 Hz and 1,300 V. The red arrows in c and d indicate the ranges of blocked force and free displacement that correspond to Fig. 2a and b. e, f, The DEA’s energy (e) and power (f) density as functions of driving frequency and voltage. This DEA’s blocked force and free displacement measurements are shown in Fig. 2a, b. g, The DEA’s instantaneous power consumption when driven at 1,400 V and 300 Hz. h, Measurement and modelling of the DEA’s temperature profile during its operation at 1,400 V and 300 Hz. i, Thermal images showing the temperature of the DEA during operation. h and i show the same experiment. Scale bars in a, b and i represent 1 cm.
Extended Data Fig. 3 Robot in-flight collision and damage sensing.
a, b, A composite image (a) and the measured DEA current (b) of a short takeoff flight without any collisions. c–f, Two takeoff flights in which the robot hits a wall during its ascent. The red circles in c and e mark the collision events and they correspond to the current spikes in d and f, respectively. g, h, A robot takeoff flight in a transparent box. The robot makes multiple collisions and the red circles in g and h relate these collisions to DEA current changes. i, j, An image sequence (i) and the measured current (j) of a flapping-wing characterization test. One robot wing falls off during the experiment and this event is detected by measuring the DEA current. Scale bars in a, c, e, g and i represent 1 cm.
Extended Data Fig. 4 DEA actuation nonlinearity.
a, FFT of the tracked wing stroke kinematics when a wing is driven at 1 Hz, 100 Hz and 280 Hz. The stroke kinematics data are taken from that shown in Fig. 3b. There is a substantial second-order harmonic for the cases of 1 Hz and 100 Hz. When the wing is driven near the system resonant frequency (280 Hz), the red circles indicate that the fundamental harmonic grows and the second harmonic is attenuated. b, Right wing stroke amplitude as a function of driving voltage and frequency. The red region represents stroke amplitudes and frequencies that cannot be achieved without constraining the DEA. The data correspond to the same experiment shown in Fig. 3f.
Extended Data Fig. 5 Repeated unstable takeoff flights.
a-c, Three takeoff flights of a robot with one DEA. In these flights, the robot flips upside down within 200 ms after lift-off owing to aerodynamic torque imbalances from the two wings. d–i, Unstable (pitch and roll) takeoff flights of a robot with two DEAs. In d–f, the robot pitches forward and eventually flips over owing to asymmetric lift forces from the front and the back robot modules. In g–i, the robot rolls sideways and flips over owing to lift force imbalances between its left and right wings. Scale bars in a–i represent 1 cm.
Extended Data Fig. 6 Illustration of robot yaw torque generation through biasing the mean wing pitch angle.
a, Illustration of wing pitch bias in a one-DEA module. The red arrows indicate the directions of the mean drag force caused by biasing the wing pitch. The net drag forces from the two wings induce a robot yaw torque. b, The inset shows the motion of a wing chord on a two-dimensional plane. The wing pitch bias causes different wing pitching motion in the up stroke and down stroke phases of the wing motion, which leads to different drag forces. c, Two one-DEA modules having the same yaw torque bias direction are assembled into a two-DEA robot. d, Two two-DEA modules having opposite yaw torque bias directions are assembled into a four-DEA robot.
Extended Data Fig. 7 Simulation of open-loop ascending flight and comparison with experimental results.
a, Coordinate system definition of the four-wing robot model. Scale bar represents 1 cm. b, Top view schematic of the four-wing robot. lx and ly denote the distance from the robot’s centre of mass to each wing’s centre of pressure. c, Comparison of measured and simulated yaw (ψ) motion. The robot makes 11 revolutions with respect to its z axis 0.8 s after takeoff. d, Comparison of measured and simulated yaw rate (\(\dot{\psi }\)). The steady-state angular velocity of the robot’s yaw rate is 17.5 revolutions per second. e, Simulated pitch (φ) and roll (θ) motion. Our simulation predicts that the steady-state oscillation with respect to the robot’s X and Y axes is smaller than 3°. f, Simulation results of the robot’s displacement after takeoff. The experimental measurement of the robot’s vertical motion is superimposed on the same graph. The data shown in c–f correspond to the simulation and experiment shown in Supplementary Video 5 and Fig. 4b, c. g–o, Dynamical simulation of robot takeoff flights under different values of body yaw torque. g, Robot altitude as a function of time. h, A zoomed-in plot of robot altitude shortly after takeoff. This plot corresponds to the red region in g. i, Robot altitude at one second after takeoff as a function of input body yaw torque. j, Robot pitch motion as a function of time. k, A zoomed-in plot of robot pitch that corresponds to the red region in j. l, Maximum robot pitch deviation as a function of input yaw torque. m, Robot roll motion as a function of time. n, A zoomed-in plot of robot roll that corresponds to the red region in m. o, Maximum robot roll deviation as a function of input yaw torque.
Extended Data Fig. 8 Three passively stable ascending flights of a robot with two DEAs.
a–c, Composite images of three one-second, open-loop ascending flights. d–g, Tracked robot altitude (d), x and y centre-of-mass position (e), pitch and roll orientation (f) and yaw rotation (g). The data shown in d–g correspond to the flight shown in a. Similarly, h–k and l–o show the tracked flight data corresponding to the flights shown in b and c, respectively. Sudden jumps in the tracking data (h, i, l and m) indicate the time at which the Vicon motion capture system loses tracking. Scale bars in a–c represent 5 cm.
Extended Data Fig. 9 Robot unbalanced takeoff flights and a failed collision recovery experiment.
a, A composite image of a 0.5-s open-loop takeoff flight captured at 3,000 frames per second. The robot pitch deviation is approximately 35° at 85 ms after takeoff. b, A composite image of a 1-s open-loop takeoff flight conducted in the Vicon motion tracking arena. c–f, Tracked robot altitude (c), x and y centre-of-mass position (d), pitch and roll orientation (e), and yaw rotation (f). The data shown in c–f correspond to the flight in b. The red circle in e illustrates the large robot pitch and roll deviation after takeoff. The red-shaded regions in c–f show the changes of robot position and orientation after it is pulled by its tether. g, An example of a failed collision recovery experiment. The robot is destabilized after making the third collision. Scale bars in a, b, and g represent 5 cm.
Extended Data Fig. 10 Controller design of the eight-wing robot and hovering flight repeatability.
a, Perspective view of the eight-wing robot with a superimposed coordinate system. The pitch (φ), roll (θ), and yaw (ψ) angles are defined with respect to the fixed X, Y and Z axes. Scale bar represents 1 cm. b, Top view schematic of the eight-wing robot. lx and ly denote the distance from the robot centre of mass to the geometric centre of each DEA. c–q, Tracked robot position (displacement relative to the origin of the Vicon motion tracking system’s coordinate system) and attitude data of five 10-s hovering flights. In these flights, we do not control the robot’s yaw motion. c, f, i, l, o, The first column shows the robot’s altitude as a function of time. d, g, j, m, p, The second column shows the robot’s lateral position as a function of time. e, h, k, n, q, The last column shows the robot’s pitch (φ) and roll (θ) motion as a function of time.
Supplementary information
Supplementary Information
This file contains Supplementary Notes 1–5, Supplementary References and a description of Supplementary Videos
Video 1
Robot flapping kinematics. This high speed video shows a robot flapping its wings at 280 Hz. The left-wing stroke and pitch amplitudes are 42° and 59°, respectively. The right-wing stroke and pitch amplitudes are 41° and 62°, respectively. The robot is driven with a 1,300 V, 280 Hz sinusoidal signal
Video 2
Collisions with obstacles of a stationary robot. This video shows collisions between an obstacle and a robot that is driven at 1,300 V and 300 Hz. In part 1, an obstacle makes collisions with the robot’s left wing. While repeated collisions reduce the wing stroke amplitudes, the DEA continues to operate without experiencing failure. In part 2, the obstacle directly presses against the DEA during its operation. This contact reduces the amplitude of the wing motion, but does not break the DEA
Video 3
DEA nonlinear actuation. This video illustrates the influence of nonlinear DEA actuation on flapping wing kinematics. Part 1 compares the flapping kinematics at 1 Hz, 100 Hz, and 280 Hz. At operating frequencies that are substantially lower than system resonance, the wing stroke motion is asymmetric due to nonlinear actuation. The motion becomes purely sinusoidal near system resonance (280 Hz) because higher order terms are attenuated by viscoelasticity. Part 2 illustrates how DEA dynamic buckling substantially reduces wing stroke amplitudes. The buckling frequency is half that of the driving frequency
Video 4
Liftoff of a robot driven by one DEA. The robot powered by one DEA demonstrates open-loop liftoff. This robot can produce sufficient lift force to take off from the ground. However, the robot is intrinsically unstable, and it has no control authority. A carbon fiber rod with a point mass is attached to the robot’s airframe to adjust its center of mass position. The robot is unstable in both the body roll and pitch axes. These two flights show that the robot quickly falls over after liftoff
Video 5
Flight of a robot driven by two DEAs. This video shows flight demonstrations of a four-wing robot powered by two DEAs. Part 1 shows unstable liftoff flights in which the robot does not rotate with respect to its body yaw axis. The robot is unstable if it does not generate sufficient yaw torque to precess. Part 2 compares experimental and simulation results of the robot’s open-loop, passively upright stable ascending flights. Quantitative flight trajectory comparisons are shown in Extended Data Figure 7. Part 3 shows three different open-loop takeoff flights. Although the driving frequency and phase of each DEA are changed, the robot is still passively upright stable. This result shows that wing-wing interactions do not substantially influence robot stability
Video 6
Robustness against in-flight collisions. This video shows the robot can survive in-flight collisions. Part 1 shows a robot flying out of a transparent cylindrical shell. The robot collides with the shell wall as it exits the cylinder. It passively recovers from this collision and continues to fly upward. Part 2 shows simultaneous flights of two robots. These robots are intentionally flown into a wall, and they do not experience damage after experiencing head-on collisions and crash landings. Part 3 shows two robots colliding with each other in mid-air. One robot recovers and flies upward after this collision
Video 7
Hovering flight demonstration through feedback control. This video shows controlled hovering flights of an eight-wing robot powered by four DEAs. Part 1 shows a 10-second flight and part 2 shows a 16-second flight. In both demonstrations, the robot’s yaw motion is not controlled. Detailed flight data is reported in Fig. 4e–i and Extended Data Figure 10i–k
Rights and permissions
About this article
Cite this article
Chen, Y., Zhao, H., Mao, J. et al. Controlled flight of a microrobot powered by soft artificial muscles. Nature 575, 324–329 (2019). https://doi.org/10.1038/s41586-019-1737-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1737-7
This article is cited by
-
An Automatic Implementation of Oropharyngeal Swab Sampling for Diagnosing Respiratory Infectious Diseases via Soft Robotic End-Effectors
Chinese Journal of Mechanical Engineering (2024)
-
A wireless controlled robotic insect with ultrafast untethered running speeds
Nature Communications (2024)
-
Light-controlled soft bio-microrobot
Light: Science & Applications (2024)
-
In silico optimization of aligned fiber electrodes for dielectric elastomer actuators
Scientific Reports (2024)
-
Slow-release effect of absolute ethanol on electro-mechano-chemical behavior and strengthening mechanism of an electric-responsive biomass paper actuator based on calcium alginate hydrogel
Cellulose (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.