Abstract
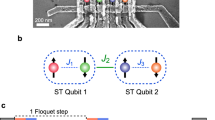
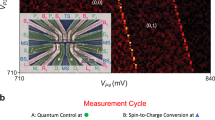
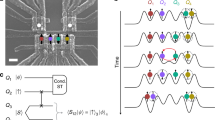
Quantum information science has the potential to revolutionize modern technology by providing resource-efficient approaches to computing1, communication2 and sensing3. Although the physical qubits in a realistic quantum device will inevitably suffer errors, quantum error correction creates a path to fault-tolerant quantum information processing4. Quantum error correction, however, requires that individual qubits can interact with many other qubits in the processor. Engineering such high connectivity can pose a challenge for platforms such as electron spin qubits5, which naturally favour linear arrays. Here we present an experimental demonstration of the transmission of electron spin states via the Heisenberg exchange interaction in an array of spin qubits. Heisenberg exchange coupling—a direct manifestation of the Pauli exclusion principle, which prevents any two electrons with the same spin state from occupying the same orbital—tends to swap the spin states of neighbouring electrons. By precisely controlling the wavefunction overlap between electrons in a semiconductor quadruple quantum dot array, we generate a series of coherent SWAP operations to transfer both single-spin and entangled states back and forth in the array without moving any electrons. Because the process is scalable to large numbers of qubits, state transfer through Heisenberg exchange will be useful for multi-qubit gates and error correction in spin-based quantum computers.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Ekert, A. & Jozsa, R. Quantum computation and Shor’s factoring algorithm. Rev. Mod. Phys. 68, 733–753 (1996).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Knill, E. Quantum computing with realistically noisy devices. Nature 434, 39–44 (2005).
Ladd, T. D. et al. Quantum computers. Nature 464, 45–53 (2010).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102–106 (2018).
Chan, K. W. et al. Assessment of a silicon quantum dot spin qubit environment via noise spectroscopy. Phys. Rev. Appl. 10, 044017 (2018).
Muhonen, J. T. et al. Quantifying the quantum gate fidelity of single-atom spin qubits in silicon by randomized benchmarking. J. Phys. Condens. Matter 27, 154205 (2015).
Huang, W. et al. Fidelity benchmarks for two-qubit gates in silicon. Nature 569, 532–536 (2019).
Zajac, D. M., Hazard, T. M., Mi, X., Nielsen, E. & Petta, J. R. Scalable gate architecture for densely packed semiconductor spin qubits. Phys. Rev. Appl. 6, 054013 (2016).
Mortemousque, P.-A. et al. Coherent control of individual electron spins in a two dimensional array of quantum dots. Preprint at https://arxiv.org/abs/1808.06180 (2018).
Mukhopadhyay, U., Dehollain, J. P., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. A 2 × 2 quantum dot array with controllable inter-dot tunnel couplings. Appl. Phys. Lett. 112, 183505 (2018).
Volk, C. et al. Loading a quantum-dot based “Qubyte” register. npj Quantum Inf. 5, 29 (2019).
Mi, X. et al. A coherent spin–photon interface in silicon. Nature 555, 599–603 (2018).
Samkharadze, N. et al. Strong spin-photon coupling in silicon. Science 359, 1123–1127 (2018).
Landig, A. J. et al. Coherent spin–photon coupling using a resonant exchange qubit. Nature 560, 179–184 (2018).
Mills, A. R. et al. Shuttling a single charge across a one-dimensional array of silicon quantum dots. Nat. Commun. 10, 1063 (2019).
Fujita, T., Baart, T. A., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. Coherent shuttle of electron-spin states. npj Quantum Inf. 3, 22 (2017).
Flentje, H. et al. Coherent long-distance displacement of individual electron spins. Nat. Commun. 8, 501 (2017).
Nakajima, T. et al. Coherent transfer of electron spin correlations assisted by dephasing noise. Nat. Commun. 9, 2133 (2018).
Baart, T. A. et al. Single-spin CCD. Nat. Nanotechnol. 11, 330–334 (2016).
Greentree, A. D., Cole, J. H., Hamilton, A. R. & Hollenberg, L. C. L. Coherent electronic transfer in quantum dot systems using adiabatic passage. Phys. Rev. B 70, 235317 (2004).
Shilton, J. M. et al. High-frequency single-electron transport in a quasi-one-dimensional GaAs channel induced by surface acoustic waves. J. Phys. Condens. Matter 8, 531–539 (1996).
Bertrand, B. et al. Fast spin information transfer between distant quantum dots using individual electrons. Nat. Nanotechnol. 11, 672–676 (2016).
Baart, T. A., Fujita, T., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. Coherent spin-exchange via a quantum mediator. Nat. Nanotechnol. 12, 26–30 (2017).
Malinowski, F. K. et al. Fast spin exchange across a multielectron mediator. Nat. Commun. 10, 1196 (2019).
Aharonov, D. & Ben-Or, M. Fault-tolerant quantum computation with constant error. In Proc. Twenty-ninth Annual ACM Symposium on Theory of Computing 176–188 (ACM Press, 1997).
Gottesman, D. Fault-tolerant quantum computation with local gates. J. Mod. Opt. 47, 333–345 (2000).
Fowler, A. G., Hill, C. D. & Hollenberg, L. C. L. Quantum-error correction on linear-nearest-neighbor qubit arrays. Phys. Rev. A 69, 042314 (2004).
Friesen, M., Biswas, A., Hu, X. & Lidar, D. Efficient multiqubit entanglement via a spin bus. Phys. Rev. Lett. 98, 230503 (2007).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Angus, S. J., Ferguson, A. J., Dzurak, A. S. & Clark, R. G. Gate-defined quantum dots in intrinsic silicon. Nano Lett. 7, 2051–2055 (2007).
Zajac, D. M., Hazard, T. M., Mi, X., Wang, K. & Petta, J. R. A reconfigurable gate architecture for Si/SiGe quantum dots. Appl. Phys. Lett. 106, 223507 (2015).
Nichol, J. M. et al. Quenching of dynamic nuclear polarization by spin–orbit coupling in GaAs quantum dots. Nat. Commun. 6, 7682 (2015).
Foletti, S., Bluhm, H., Mahalu, D., Umansky, V. & Yacoby, A. Universal quantum control of two-electron spin quantum bits using dynamic nuclear polarization. Nat. Phys. 5, 903–908 (2009).
Taylor, J. M. et al. Relaxation, dephasing, and quantum control of electron spins in double quantum dots. Phys. Rev. B 76, 035315 (2007).
Shulman, M. D. et al. Suppressing qubit dephasing using real-time Hamiltonian estimation. Nat. Commun. 5, 5156 (2014).
Bluhm, H., Foletti, S., Mahalu, D., Umansky, V. & Yacoby, A. Enhancing the coherence of a spin qubit by operating it as a feedback loop that controls its nuclear spin bath. Phys. Rev. Lett. 105, 216803 (2010).
Barthel, C., Reilly, D. J., Marcus, C. M., Hanson, M. P. & Gossard, A. C. Rapid single-shot measurement of a singlet-triplet qubit. Phys. Rev. Lett. 103, 160503 (2009).
Studenikin, S. et al. Enhanced charge detection of spin qubit readout via an intermediate state. Appl. Phys. Lett. 101, 233101 (2012).
Reed, M. D. et al. Reduced sensitivity to charge noise in semiconductor spin qubits via symmetric operation. Phys. Rev. Lett. 116, 110402 (2016).
Martins, F. et al. Noise suppression using symmetric exchange gates in spin qubits. Phys. Rev. Lett. 116, 116801 (2016).
Orona, L. A. et al. Readout of singlet–triplet qubits at large magnetic field gradients. Phys. Rev. B 98, 125404 (2018).
Wang, X. et al. Composite pulses for robust universal control of singlet–triplet qubits. Nat. Commun. 3, 997 (2012).
Nichol, J. M., Orona, L. A., Harvey, S. P., Fallahi, S., Gardner, G. C., Manfra, M. J. & Yacoby, A. High-fidelity entangling gate for double-quantum-dot spin qubits. npj Quantum Inf. 3, 3 (2017).
Sigillito, A. J., Gullans, M. J., Edge, L. F., Borselli, M. & Petta, J. R. Coherent transfer of quantum information in silicon using resonant SWAP gates. Preprint at https://arxiv.org/abs/1906.04512 (2019).
Acknowledgements
This work was sponsored the Defense Advanced Research Projects Agency under grant number D18AC00025 and the Army Research Office under grant numbers W911NF-16-1-0260 and W911NF-19-1-0167. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the US Government. The US Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.
Author information
Authors and Affiliations
Contributions
Y.P.K., H.Q. and J.M.N. fabricated the device and performed the experiments. S.F., G.C.G. and M.J.M. grew and characterized the AlGaAs/GaAs heterostructure. All authors discussed and analysed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Andrew Dzurak and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Experimental data showing four-dot transfer of entangled states.
a, Schematic of the four-dot entangled-state transfer process. b, Interleaved data showing (I, ΔB, I), (S23, ΔB, S23) and (S23, S12, ΔB, S12, S23) measurements. c, Data from repetition 2, plotted on the same horizontal axis. d, Time evolution of the different magnetic gradients. Because the gradients result from different nuclear-spin configurations, they have different values and time evolutions. Error bars are fitting errors.
Extended Data Fig. 2 Results of the three-dot state transfer simulation.
The simulation results show good agreement with the data in Fig. 2 (see Methods). a, Simulated right-side measurements for the S34, S34, S23, S23, S34, S34 sequence. b, Simulated left-side measurements for the same sequence. c, Simulated right-side measurements for the three-dot state transfer control sequence with I in place of S34. d, Simulated left-side measurements for the same sequence. e, Simulated right-side measurements for the three-dot control sequence with I in place of S23. f, Simulated left-side measurements for the same sequence.
Extended Data Fig. 4 Calibration of SWAP operations by pulse concatenation.
Each panel shows the results of concatenating specific operations. Each SWAP operation is implemented by a separate voltage pulse to a barrier gate. a, Right-side measurements for repeated S12 operations. Prior to the first step, the array was initialized in the \(\left|\downarrow \uparrow \downarrow \uparrow \right\rangle \) state. b, Left-side measurements for repeated S12 operations. c, Right-side measurements for repeated S34 operations. Prior to the first step, the array was initialized in the \(\left|\downarrow \uparrow \downarrow \uparrow \right\rangle \) state. d, Left-side measurements for repeated S34 operations. e, Right-side measurements for repeated S23 operations. The array was initialized in the \(\left|\uparrow \uparrow \downarrow \uparrow \right\rangle \) state. We did not record left-side measurements for this sequence. In all panels, vertical black lines indicate error bars, which represent the standard deviation of 64 repetitions of the average of 64 single-shot measurements of each pulse configuration.
Extended Data Fig. 5 Simulated fidelity of SWAP pulses for entangled states.
a, Simulated ensemble-averaged state fidelity after applying a simulated realistic S23 operation to the initial state \(\left|{\psi }_{0}\right\rangle =\frac{1}{\sqrt{2}}\left(\left|\uparrow \uparrow \uparrow \downarrow \right\rangle -\left|\uparrow \uparrow \downarrow \uparrow \right\rangle \right)\). The target state is \(\left|{\psi }_{t}\right\rangle =\frac{1}{\sqrt{2}}\left(\left|\uparrow \uparrow \uparrow \downarrow \right\rangle -\left|\uparrow \downarrow \uparrow \uparrow \right\rangle \right)\). The horizontal axis represents the free-evolution time of the state under the influence of the magnetic gradient after the exchange operation. The fidelity is averaged over 2,000 different simulations of magnetic and electrical noise. The state fidelity has a maximum of about 0.65, and it quickly decays to 0.5. The decay results from the fluctuating magnetic gradient. b, Calculated characteristic single-shot state fidelity for one simulation of the noise. For specific times, the state fidelity returns to about 0.9. The magnetic gradient is assumed to be stable in each realization of the sequence.
Extended Data Fig. 6 Preparation of quadruple quantum dot state.
a, Verification of exchange oscillations on the left side. Initializing the left side in the \(\left|\uparrow \uparrow \right\rangle \) state before a T12 pulse yields no exchange oscillations. Initialization in the \(\left|\downarrow \uparrow \right\rangle \) state shows exchange oscillations. b, Initializing the right side in the \(\left|\uparrow \uparrow \right\rangle \) state before a T34 pulse yields no exchange oscillations. Initialization in the \(\left|\downarrow \uparrow \right\rangle \) state shows exchange oscillations. c, Verification of the ground-state orientation of the right side. We load the left side in the \(\left|\uparrow \uparrow \right\rangle \) state and the right side by adiabatic separation of the singlet state, which gives either \(\left|\uparrow \downarrow \right\rangle \) or \(\left|\downarrow \uparrow \right\rangle \), depending on the sign of the gradient. We pulse T23 to induce exchange between the middle two spins. Dynamic nuclear polarization with singlets yields no oscillations, whereas pumping with triplets yields oscillations. These data confirm that the separated singlet state evolves to the \(\left|\downarrow \uparrow \right\rangle \) state under triplet pumping for the right side. d, Verification of the ground state of the left side. We initialize the array by separating singlets on both sides. In the case of triplet pumping on the right side, the third spin is \(\left|\downarrow \right\rangle \), so the second spin must be \(\left|\uparrow \right\rangle \) in order to generate exchange oscillations with a T23 pulse, as measured on the left side. Singlet pumping on the left side yields no exchange oscillations. e, The same initialization and pulses as in e, but measured on the right side. In all cases, \({P}_{{\rm{S}}}^{{\rm{L}}\left({\rm{R}}\right)}\) indicates the singlet return probability measured on the left (right) side.
Rights and permissions
About this article
Cite this article
Kandel, Y.P., Qiao, H., Fallahi, S. et al. Coherent spin-state transfer via Heisenberg exchange. Nature 573, 553–557 (2019). https://doi.org/10.1038/s41586-019-1566-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1566-8
This article is cited by
-
Dephasing effects on nonclassical correlations in two-qubit Heisenberg spin chain model with anisotropic spin–orbit interactions
Applied Physics B (2024)
-
Progress in quantum teleportation
Nature Reviews Physics (2023)
-
Probing two-qubit capacitive interactions beyond bilinear regime using dual Hamiltonian parameter estimations
npj Quantum Information (2023)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
Spreading entanglement through pairwise exchange interactions
Quantum Information Processing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.