Abstract
In the quest to understand high-temperature superconductivity in copper oxides, debate has been focused on the pseudogap—a partial energy gap that opens over portions of the Fermi surface in the ‘normal’ state above the bulk critical temperature1. The pseudogap has been attributed to precursor superconductivity, to the existence of preformed pairs and to competing orders such as charge-density waves1,2,3,4. A direct determination of the charge of carriers as a function of temperature and bias could help resolve among these alternatives. Here we report measurements of the shot noise of tunnelling current in high-quality La2−xSrxCuO4/La2CuO4/La2−xSrxCuO4 (LSCO/LCO/LSCO) heterostructures fabricated using atomic layer-by-layer molecular beam epitaxy at several doping levels. The data delineate three distinct regions in the bias voltage–temperature space. Well outside the superconducting gap region, the shot noise agrees quantitatively with independent tunnelling of individual charge carriers. Deep within the superconducting gap, shot noise is greatly enhanced, reminiscent of multiple Andreev reflections5,6,7. Above the critical temperature and extending to biases much larger than the superconducting gap, there is a broad region in which the noise substantially exceeds theoretical expectations for single-charge tunnelling, indicating pairing of charge carriers. These pairs are detectable deep into the pseudogap region of temperature and bias. The presence of these pairs constrains current models of the pseudogap and broken symmetry states, while phase fluctuations limit the domain of superconductivity.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data used to produce the figures in the main text as well as in the Extended Data are provided with the paper. Data are also available online at https://doi.org/10.6084/m9.figshare.8247140 through the Springer Nature Research Data Support Service.
References
Keimer, B., Kivelson, S. A., Norman, M. R., Uchida, S. & Zaanen, J. From quantum matter to high-temperature superconductivity in copper oxides. Nature 518, 179–186 (2015).
Emery, V. J. & Kivelson, S. A. Importance of phase fluctuations in superconductors with small superfluid density. Nature 374, 434–437 (1995).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Uchida, S.-i. Forefront in the elucidation of the mechanism of high-temperature superconductivity. Jpn. J. Appl. Phys. 51, 010002 (2012).
Cuevas, J. C. & Fogelström, M. Shot noise and multiple Andreev reflections in d-wave superconductors. Phys. Rev. Lett. 89, 227003 (2002).
Dieleman, P., Bukkems, H. G., Klapwijk, T. M., Schicke, M. & Gundlach, K. H. Observation of Andreev reflection enhanced shot noise. Phys. Rev. Lett. 79, 3486–3489 (1997).
Ronen, Y. et al. Charge of a quasiparticle in a superconductor. Proc. Natl Acad. Sci. USA 113, 1743–1748 (2016).
Loeser, A. G. et al. Excitation gap in the normal state of underdoped Bi2Sr2CaCu2O8+δ. Science 273, 325–329 (1996).
Ding, H. et al. Spectroscopic evidence for a pseudogap in the normal state of underdoped high-T c superconductors. Nature 382, 51–54 (1996).
Kondo, T. et al. Disentangling Cooper-pair formation above the transition temperature from the pseudogap state in the cuprates. Nat. Phys. 7, 21–25 (2011).
Reber, T. J. et al. Prepairing and the “filling” gap in the cuprates from the tomographic density of states. Phys. Rev. B 87, 060506 (2013).
Gomes, K. K. et al. Visualizing pair formation on the atomic scale in the high-T c superconductor Bi2Sr2CaCu2O8+δ. Nature 447, 569–572 (2007).
Kohsaka, Y. et al. Visualization of the emergence of the pseudogap state and the evolution to superconductivity in a lightly hole-doped Mott insulator. Nat. Phys. 8, 534–538 (2012).
Lee, J. et al. Spectroscopic fingerprint of phase-incoherent superconductivity in the cuprate pseudogap state. Science 325, 1099–1103 (2009).
Bilbro, L. S. et al. Temporal correlations of superconductivity above the transition temperature in La2−xSrxCuO4 probed by terahertz spectroscopy. Nat. Phys. 7, 298–302 (2011).
Wang, Y., Li, L. & Ong, N. P. Nernst effect in high-T c superconductors. Phys. Rev. B 73, 024510 (2006).
Li, L. et al. Diamagnetism and Cooper pairing above T c in cuprates. Phys. Rev. B 81, 054510 (2010).
Božović, I., He, X., Wu, J. & Bollinger, A. T. Dependence of the critical temperature in overdoped copper oxides on superfluid density. Nature 536, 309–311 (2016).
de Picciotto, R. et al. Direct observation of a fractional charge. Nature 389, 162–164 (1997).
Saminadayar, L., Glatti, D. C., Jin, Y. & Etienne, B. Observation of the e/3 fractionally charged Laughlin quasiparticle. Phys. Rev. Lett. 79, 2526–2529 (1997).
Negri, O., Zaberchik, M., Drachuck, G., Keren, A. & Reznikov, M. Zero energy states at a normal-metal/cuprate-superconductor interface probed by shot noise. Phys. Rev. B 97, 214504 (2018).
Bastiaans, K. M. et al. Charge trapping and super-Poissonian noise centres in a cuprate superconductor. Nat. Phys. 14, 1183–1187 (2018).
Berg, E., Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Striped superconductors: how spin, charge and superconducting orders intertwine in the cuprates. New J. Phys. 11, 115004 (2009).
Lee, P. A. Amperean pairing and the pseudogap phase of cuprate superconductors. Phys. Rev. X 4, 031017 (2014).
Hamidian, M. H. et al. Detection of a Cooper-pair density wave in Bi2Sr2CaCu2O8+x. Nature 532, 343–347 (2016).
Božović, I., Logvenov, G., Verhoeven, M., Caputo, P. & Goldobin, E. No mixing of superconductivity and antiferromagnetism in a high-temperature superconductor. Nature 422, 873–875 (2003).
Deutscher, G. Coherence and single-particle excitations in the high-temperature superconductors. Nature 397, 410–412 (1999).
Andersen, O. K., Liechtenstein, A. I., Jepsen, O. & Paulsen, F. LDA energy bands, low-energy Hamiltonians, t′, t″, t ⊥(k), and J ⊥. J. Phys. Chem. Solids 56, 1573–1591 (1995).
Sato, Y. et al. Thermodynamic evidence for a nematic phase transition at the onset of the pseudogap in YBa2Cu3Oy. Nat. Phys. 13, 1074–1078 (2017).
Wu, J., Bollinger, A. T., He, X. & Božović, I. Spontaneous breaking of rotational symmetry in copper oxide superconductors. Nature 547, 432–435 (2017).
Božović, I. Atomic-layer engineering of superconducting oxides: yesterday, today, tomorrow. IEEE Trans. Appl. Supercond. 11, 2686–2695 (2001).
Gozar, A. et al. High-temperature interface superconductivity between metallic and insulating copper oxides. Nature 455, 782–785 (2008).
Smadici, S. et al. Superconducting transition at 38 K in insulating-overdoped La2CuO4–La1.64Sr0.36CuO4 superlattices: evidence for interface electronic redistribution from resonant soft X-ray scattering. Phys. Rev. Lett. 102, 107004 (2009).
Logvenov, G., Gozar, A. & Božović, I. High-temperature superconductivity in a single copper-oxygen plane. Science 326, 699–702 (2009).
Bollinger, A. T. et al. Superconductor–insulator transition in La2−xSrxCuO4 at the pair quantum resistance. Nature 472, 458–460 (2011).
Yacoby, Y., Zhou, H., Pindak, R. & Božović, I. Atomic-layer synthesis and imaging uncover broken inversion symmetry in La2−xSrxCuO4 films. Phys. Rev. B 87, 014108 (2013).
Božović, I. et al. Giant proximity effect in cuprate superconductors. Phys. Rev. Lett. 93, 157002 (2004).
Tewari, S. et al. Fast and accurate shot noise measurements on atomic-size junctions in the MHz regime. Rev. Sci. Instrum. 88, 093903 (2017).
Rousseeuw, P. J. & Leroy, A. M. Robust Regression and Outlier Detection. (Wiley, 2005).
Cron, R., Goffman, M. F., Esteve, D. & Urbina, C. Multiple-charge-quanta shot noise in superconducting atomic contacts. Phys. Rev. Lett. 86, 4104–4107 (2001).
Chakravarty, S., Sudbø, A., Anderson, P. W. & Strong, S. Interlayer tunneling and gap anisotropy in high-temperature superconductors. Science 261, 337–340 (1993).
Greibe, T., Bauch, T., Wilson, C. & Delsing, P. Improvement of chip design to reduce resonances in subgap regime of Josephson junctions. J. Phys. Conf. Ser. 150, 052063 (2009).
Greibe, T. et al. Are “pinholes” the cause of excess current in superconducting tunnel junctions? A study of Andreev current in highly resistive junctions. Phys. Rev. Lett. 106, 097001 (2011).
Uzawa, Y. & Wang, Z. Coherent multiple charge transfer in a superconducting NbN tunnel junction. Phys. Rev. Lett. 95, 017002 (2005).
Acknowledgements
Y. Zhang helped with TEM sample preparation and S. Yang with STEM EDX spectroscopy data acquisition. We are also grateful to P. Lee, S. Kivelson, D. Scalapino, J. Kono, M. Foster, T. C. Wu, J. C. Cuevas, P. Samuelsson, A. Gozar and I. Drozdov for their comments and questions. The research at Brookhaven National Laboratory, including heterostructure synthesis and characterization and device fabrication, was supported by the US Department of Energy, Basic Energy Sciences, Materials Sciences and Engineering Division. X.H. was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant GBMF4410. The work at the University of Connecticut was supported by the US state of Connecticut. The research at Rice University was supported by the US Department of Energy, Basic Energy Sciences, Experimental Condensed Matter Physics award DE-FG02-06ER46337. Some of the Rice noise measurement hardware were acquired through National Science Foundation award DMR-1704264.
Author information
Authors and Affiliations
Contributions
X.H. and I.B. synthesized the high-temperature-superconductor heterostructures. A.T.B. and P.Z. fabricated the tunnelling and Hall bar devices. P.Z., L.C. and Y.L. built the noise measurement system. P.Z. performed and analysed the noise measurements. M.-G.H. and Y.Z. conducted the TEM studies. D.N. and I.B. designed the experiments. I.S. performed differential conductance measurements down to dilution refrigerator temperatures. All authors contributed to writing the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
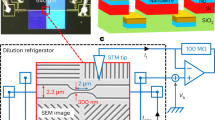
Extended Data Fig. 1 Device fabrication process.
a, LSCO/LCO/LSCO film is grown on top of an LSAO substrate with a thin layer of in situ-deposited Au covering the film. b, The film is etched into about 20-μm-sized bars defined photolithographically. This is a deep etch all the way into the substrate. c, A second dry etch step removes part of the top LSCO and middle LCO layers, and stops in the middle of the bottom LSCO layer, creating mesas of 10–20 μm in diameter. d, A thick layer of Al2O3 (100 nm) is evaporated to isolate the future Au contacts (all 150 nm thick, one at the top and two at the bottom), to avoid parallel conduction paths. e, Contacts are defined lithographically and Au is evaporated to make contact with the top and bottom LSCO layers. f, A false-coloured scanning electron microscopy image of the device. g, STEM cross-section of a representative device structure, showing the atomic perfection of the ALL-MBE process.
Extended Data Fig. 2 Transport in LSCO/LCO/LSCO (x = 0.15) film and tunnel junction properties.
a, R–T measurement on the Hall bar device fabricated in this film shows the superconducting transition temperature Tc = 38 K. b, Tunnelling differential conductance in a trilayer junction fabricated in this film. c, log–log plot of the I–V characteristics of two x = 0.15 tunnel junction devices, demonstrating device-to-device reproducibility and lack of any supercurrent down to pA levels at dilution refrigerator temperatures.
Extended Data Fig. 3 Bias-dependent noise and differential conductance.
a–h, Noise data from Fig. 3 reproduced with accompanying non-normalized differential conductance data.
Extended Data Fig. 4 Electrical circuit diagrams for the shot-noise measurement setup.
a, Diagram of the two-channel cross-correlation method. b, The equivalent circuit diagram can be modeled as an RSCP circuit, where is is the noise source, RS is the (bias-dependent) differential resistance of the sample, CP is the parasitic capacitance in the system, and vna is the input voltage noise of the preamplifier.
Extended Data Fig. 5 RSCP model fitting, noise PSD calibration and example spectra of an LSCO tunnel junction.
a, The PSD of the JN voltage noise in a 2.17 kΩ resistor at T = 300 K, measured by the cross-correlation method. The red line is a fit based on the RSCP model. b, The JN voltage noise of various resistors at 300 K. The voltage noise SV has a simple linear dependence on the resistance of the resistor that is used as a calibration reference. c, The JN noise is also linearly dependent on temperature for a fixed resistor (2.17 kΩ). d, For a fixed resistor (2.17 kΩ), the JN noise is independent of the bias current, as expected for a macroscopic diffusive conductor. e–j, Example spectra of an LSCO tunnel junction for x = 0.15, recorded at T = 50 K. The d.c. bias current is marked for each panel. Red dashed lines are fits based on the RSCP circuit model. The sharp spikes result from environmental pickup of specific frequencies, and the fitting procedure is not influenced by these. Such environmental pickup is larger at the lowest temperatures below Tc.
Extended Data Fig. 6 Noise ratios as a function of temperature and bias.
a–h,The noise ratio for the four LSCO devices featured in Fig. 1 at various doping levels as indicated, measured below Tc (a–d) and above Tc (e–h). i–p, The noise ratio for the other four LSCO devices at various doping levels as indicated, measured below Tc (i–l) and above Tc (m–p).
Extended Data Fig. 7 The variance in PSD with different averaging times.
a, A relatively flat region (red) is selected to analyse the distribution of variations in the PSD. Sharp spikes are the environmental pickup of discrete frequencies; these are not used in the fitting procedure. b, c, The normalized PSD distribution in the selected region for a 96 s averaging time (b) and a 6 s averaging time (c). The red line is the Gaussian fit to the distribution. d, The standard deviation of the distribution for different averaging times.
Extended Data Fig. 8 Shot noise in a Nb tunnel junction.
a–d, Noise measurements (blue points with error bars) and differential conductance (green) as a function of bias and temperature for a commercial Nb/AlOx/Nb tunnel junction that exhibits Josephson supercurrent below Tc = 9 K. The error bars combine in quadrature the systematic uncertainty described in Methods section ‘Error analysis’ and the standard error of the noise fitting parameter for each bias. e, Inferred pair fraction z as a function of bias and temperature for this device. The red dash–dotted line is the superconducting gap region outside which z = 0 is expected from the BCS theory for the measured value of Tc. The green dashed line is V = kBT/e. As eV/kBT → 0, determining z via noise measurements is not possible (see Methods). The grey region indicates where the uncertainty in z exceeds 0.5, on the basis of the systematic standard deviation of the noise ratio of ±0.015, as described in Methods section ‘Error analysis’.
Extended Data Fig. 9 Noise as a function of current, and comparison with Andreev reflection.
Noise data from Fig. 3 plotted as a function of bias current instead of bias voltage, and the noise data at 5 K compared with expectations of a very simplified MAR model. a–d, The red dashed line shows the single-charge tunnelling Poissonian expectation 2eIcoth(eV(I)/2kBT), based on the measured I(V) at each temperature. e, f, The red traces assume a bias-dependent effective charge based on kinetically allowed Andreev processes (q∗ = ne with 2Δ/n < eV < 2Δ/(n − 1), for n = 2, 3, …) for a fixed isotropic gap Δ, combined with a finite temperature expectation for the noise SI = 2q∗(V) × Icoth(q∗(V) × V/2kBT).
Rights and permissions
About this article
Cite this article
Zhou, P., Chen, L., Liu, Y. et al. Electron pairing in the pseudogap state revealed by shot noise in copper oxide junctions. Nature 572, 493–496 (2019). https://doi.org/10.1038/s41586-019-1486-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1486-7
This article is cited by
-
Superconducting tunnel junctions with layered superconductors
Quantum Frontiers (2024)
-
Absence of a BCS-BEC crossover in the cuprate superconductors
npj Quantum Materials (2023)
-
High-T\(_c\) Cuprates: a Story of Two Electronic Subsystems
Journal of Superconductivity and Novel Magnetism (2022)
-
Quantum magnetic monopole condensate
Communications Physics (2021)
-
Superconductor-insulator transition in space charge doped one unit cell Bi2.1Sr1.9CaCu2O8+x
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.