Abstract
The biophysical relationships between sensors and actuators1,2,3,4,5 have been fundamental to the development of complex life forms. Swimming organisms generate abundant flows that persist in aquatic environments6,7,8,9,10,11,12,13, and responding promptly to external stimuli is key to survival14,15,16,17,18,19. Here we present the discovery of ‘hydrodynamic trigger waves’ in cellular communities of the protist Spirostomum ambiguum that propagate—in a manner similar to a chain reaction20,21,22—hundreds of times faster than their swimming speed. By coiling its cytoskeleton, Spirostomum can contract its long body by 60% within milliseconds23, experiencing accelerations that can reach forces of 14g. We show that a single cellular contraction (the transmitter) generates long-ranged vortex flows at intermediate Reynolds numbers that can, in turn, trigger neighbouring cells (the receivers). To measure the sensitivity to hydrodynamic signals in these receiver cells, we present a high-throughput suction–flow device for probing mechanosensitive ion channels24 by back-calculating the microscopic forces on the cell membrane. We analyse and quantitatively model the ultra-fast hydrodynamic trigger waves in a universal framework of antenna and percolation theory25,26, and reveal a phase transition that requires a critical colony density to sustain collective communication. Our results suggest that this signalling could help to organize cohabiting communities over large distances and influence long-term behaviour through gene expression (comparable to quorum sensing16). In more immediate terms, because contractions release toxins27, synchronized discharges could facilitate the repulsion of large predators or immobilize large prey. We postulate that numerous aquatic organisms other than protists could coordinate their behaviour using variations of hydrodynamic trigger waves.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon request.
Code availability
The computer codes used in this paper are available from the corresponding authors upon request.
References
Weis-Fogh, T. & Amos, W. B. Evidence for a new mechanism of cell motility. Nature 236, 301–304 (1972).
Mahadevan, L. & Matsudaira, P. Motility powered by supramolecular springs and ratchets. Science 288, 95–99 (2000).
Ryu, S., Pepper, R., Nagai, M. & France, D. Vorticella: a protozoan for bio-inspired engineering. Micromachines 8, 4 (2016).
Ilton, M. et al. The principles of cascading power limits in small, fast biological and engineered systems. Science 360, eaao1082 (2018).
Marshall, W. F. Origins of cellular geometry. BMC Biol. 9, 57 (2011).
Purcell, E. M. Life at low Reynolds number. Am. J. Phys. 45, 3 (1977).
Lauga, E. & Powers, T. R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72, 096601 (2009).
Koch, D. L. & Subramanian, G. Collective hydrodynamics of swimming microorganisms: living fluids. Annu. Rev. Fluid Mech. 43, 637–659 (2011).
Marchetti, M. et al. Hydrodynamics of soft active matter. Rev. Mod. Phys. 85, 1143 (2013).
Elgeti, J., Winkler, R. G. & Gompper, G. Physics of microswimmers—single particle motion and collective behavior: a review. Rep. Prog. Phys. 78, 056601 (2015).
Bechinger, C. et al. Active particles in complex and crowded environments. Rev. Mod. Phys. 88, 045006 (2016).
Winkler, R. G. Low Reynolds number hydrodynamics and mesoscale simulations. Eur. Phys. J. Spec. Top. 225, 2079–2097 (2016).
Mathijssen, A. J. T. M., Doostmohammadi, A., Yeomans, J. M. & Shendruk, T. N. Hydrodynamics of micro-swimmers in films. Fluid Mech. 806, 35–70 (2016).
Latz, M. I. et al. Bioluminescent response of individual dinoflagellate cells to hydrodynamic stress measured with millisecond resolution in a microfluidic device. J. Exp. Biol. 211, 2865–2875 (2008).
Kiørboe, T., Andersen, A., Langlois, V. J., Jakobsen, H. H. & Bohr, T. Mechanisms and feasibility of prey capture in ambush-feeding zooplankton. Proc. Natl Acad. Sci. USA 106, 12394–12399 (2009).
Kim, M. K., Ingremeau, F., Zhao, A., Bassler, B. L. & Stone, H. A. Local and global consequences of flow on bacterial quorum sensing. Nat. Microbiol. 1, 15005 (2016).
Rodesney, C. A. et al. Mechanosensing of shear by Pseudomonas aeruginosa leads to increased levels of the cyclic-di-GMP signal initiating biofilm development. Proc. Natl Acad. Sci. USA 114, 5906–5911 (2017).
Ohmura, T. et al. Simple mechanosense and response of cilia motion reveal the intrinsic habits of ciliates. Proc. Natl Acad. Sci. USA 115, 3231–3236 (2018).
Wan, K. Y. & Goldstein, R. E. Time irreversibility and criticality in the motility of a flagellate microorganism. Phys. Rev. Lett. 121, 058103 (2018).
Tyson, J. J. & Keener, J. P. Singular perturbation theory of traveling waves in excitable media (a review). Physica D 32, 327–361 (1988).
Prindle, A. et al. Ion channels enable electrical communication in bacterial communities. Nature 527, 59–63 (2015).
Gelens, L., Anderson, G. A. & Ferrell, J. E. Jr. Spatial trigger waves: positive feedback gets you a long way. Mol. Biol. Cell 25, 3486–3493 (2014).
Hawkes, R. B. & Holberton, D. V. Myonemal contraction of Spirostomum. I. Kinetics of contraction and relaxation. J. Cell. Physiol. 84, 225–235 (1974).
Phillips, R., Kondev, J., Theriot, J. & Garcia, H. Physical Biology of the Cell (Garland Science, 2012).
Xia, W. & Thorpe, M. F. Percolation properties of random ellipses. Phys. Rev. A Gen. Phys. 38, 2650–2656 (1988).
Takeuchi, K. A., Kuroda, M., Chaté, H. & Sano, M. Directed percolation criticality in turbulent liquid crystals. Phys. Rev. Lett. 99, 234503 (2007).
Buonanno, F., Guella, G., Strim, C. & Ortenzi, C. Chemical defence by mono-prenyl hydroquinone in a freshwater ciliate, Spirostomum ambiguum. Hydrobiologia 684, 97–107 (2012).
Verchot-Lubicz, J. & Goldstein, R. E. Cytoplasmic streaming enables the distribution of molecules and vesicles in large plant cells. Protoplasma 240, 99–107 (2010).
Nüchter, T., Benoit, M., Engel, U., Ozbek, S. & Holstein, T. W. Nanosecond-scale kinetics of nematocyst discharge. Curr. Biol. 16, R316–R318 (2006).
Hawking, S. W. A Brief History of Time (Bantam Books, 1988).
Cortez, R., Fauci, L. & Medovikov, A. The method of regularized Stokeslets in three dimensions: analysis, validation, and application to helical swimming. Phys. Fluids 17, 031504 (2005).
K. Hausmann, Food acquisition, food ingestion and food digestion by protists. Jpn. J. Protozool. 35, 85–95 (2002).
Hines, H. N., Onsbring, H., Ettema, T. J. G. & Esteban, G. F. Molecular investigation of the ciliate Spirostomum semivirescens, with first transcriptome and new geographical records. Protist 169, 875–886 (2018).
Hamilton, T. C., Thompson, J. M. & Eisenstein, E. M. Quantitative analysis of ciliary and contractile responses during habituation training in Spirostomum ambiguum. Behav. Biol. 12, 393–407 (1974).
Acknowledgements
We thank S. Coyle and D. Krishnamurthy and all members of the Prakash Laboratory for discussions. A.J.T.M.M. acknowledges funding from the Human Frontier Science Program (Fellowship LT001670/2017). This work was supported by NSF CCC grant (DBI-1548297) (M.P.), US Army Research Office grant (W911NF-15-1-0358) (M.P.), CZI BioHub Investigator Program (M.P.), the Howard Hughes Medical Institute (M.P.) and NSF grant (award number 1817334) (M.S.B.). We thank M. Gruber for the scientific illustration of S. ambiguum shown in Fig. 1a.
Author information
Authors and Affiliations
Contributions
A.J.T.M.M., M.S.B. and M.P. designed the research, A.J.T.M.M., M.S.B. and J.C. performed the experiments, A.J.T.M.M. analysed the data, A.J.T.M.M. carried out the simulations and theory, A.J.T.M.M., M.S.B., J.C. and M.P. wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Measurement of electrically stimulated Spirostomum contraction dynamics.
a, Diagram of experimental setup. b, Phase diagram of organism response to electric signals. The median behaviour of about 20 organisms is shown for each data point; this is repeated in n = 20 × 25 independent experiments with new organisms, for different pulse strengths and duration. c, Typical kinematics of organism length after stimulation at E = 1.5 kV m−1 and τΕ = 100 ms. Inset, collapse of kinematics, when normalizing the cell length and lining up the onsets of contraction at t = 0. d, Perception and contraction time against stimulus intensity, with τΕ = 100 ms. Points show the mean of an ensemble of about 20 independent organisms for each pulse strength, and shaded regions are error bars of 95% confidence level. The inset shows the same data on a log scale.
Extended Data Fig. 2 Experimental data of the generation of flow during contractions.
Data are the same as those presented in Fig. 2c, d, but without the theory data superimposed. The red arrows that denote the long axis of the body are kept for reference. n = 46 experiments. a, PIV measurements of the flow averaged for 40 ms after the onset of contraction. b, Experimental tracer dynamics. White lines are obtained from superposing image frames with FlowTrace software, and the coloured lines are digital PTV particle trajectories obtained with TrackMate software.
Extended Data Fig. 3 Comparison of Stokes flow and LNS flow.
Stokes flow, ReT ≪ 1; linearized Navier Stokes flow, ReT ≈ 50. a, Flow due to a point force (Stokeslet solution) (Supplementary equation 10). b, LNS tensor solution (Supplementary equation 16). c, d, Contraction flow in a liquid film (Supplementary equation 27); for high (1,000× water) (c) and low (water) (d) viscosities, with m = ±100 image reflections and k = ±5 grid points on the elongated body. In this figure, τc is kept constant at 5 ms for comparison of the high- and low-viscosity cases. The Stokes solution has open stream lines, but the LNS solution features vortices that spread out over time. Colours show flow magnitude and arrows are stream lines.
Extended Data Fig. 4 Comparison of experimental and theoretical flows induced by a cell contracting in a liquid film.
Flow velocities are shown, as a function of distance from the organism. Results were obtained experimentally (PIV) and theoretically (LNS model; Supplementary equation 27), and both are averaged for the 40 ms after the onset of contraction. These are the same data as are shown in Fig. 2c, shown differently to aid quantitative comparison. Blue and red colours indicate flows in the longitudinal and transverse directions, respectively, of the elongated cell, which is shown in green for reference. Points indicate experimental data and lines indicate the model. n = 46 experiments.
Extended Data Fig. 5 Dissipation of the spatially averaged flow velocity over time.
Results are obtained from the LNS model (Supplementary equation 27) for a low viscosity medium (water, ν = 1 mm2 s−1). The average is taken over all spatial points x, y ∈ [−1,1] mm, at the centre of the liquid film, z = 0 (the same data as are presented in Supplementary Video 5). Speeds are normalized with respect to their maximum. These simulation data may be compared directly with the experimental data in Fig. 2e.
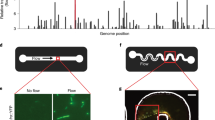
Extended Data Fig. 6 Diagram of the high-throughput device developed for measuring the rheosensitivity of cells.
The device is not shown to scale. Liquid with suspended organisms is held in a cylindrical container, with a narrow flow chamber in the bottom compartment. Liquid is drawn into the chamber on the sides and pumped out from a central tube. This creates an axisymmetric Jeffery–Hamel flow (Supplementary equation 29). a, Three-dimensional diagram of the experimental setup. b, Side view and schematic of flow profile. The organism (green) is stretched because the anterior flow is stronger than the posterior flow (Supplementary equation 33).
Extended Data Fig. 7 Collective hydrodynamic signalling.
a, Example of a configuration of organisms A–O. The first cell to contract is A (blue), and the last are K, L, M and N (red). Organism O is not triggered (grey). The circle is used to compute the organism density around cell D (green). b, Connectivity graph of the same configuration as shown in a.
Extended Data Fig. 8 Effect of boundary conditions on the percolation threshold.
Three geometries are considered: (1) organisms in bulk, without confining surfaces (blue). This situation is presented in the main text. (2) Organisms at z = 0 near a liquid–air interface at z = 50 μm (green). Here, one reflecting image system is used. (3) Organisms in a liquid film, between liquid–air interfaces at z = ±50 μm, for which a series of reflecting image systems is used (magenta). In all three cases, the cells are located at z = 0 and oriented parallel to the x–y plane, for comparison. a, Contours of the critical strain rate \({\dot{\gamma }}_{{\rm{c}}}\) = 100 s−1 for each of the three geometries (compare with Fig. 4c). This region of influence is largest in a film. b, Simulated percolation probability versus organism density for each geometry (compare with Fig. 4b). The percolation threshold is lowest in the film. Centre values show the mean of an ensemble of n = 100 independent simulations, each with about 103 cells, and the error bars indicate two s.e.m.
Extended Data Fig. 9 Mixing of toxins during a hydrodynamic trigger wave.
Simulated for n = 123 organisms in an approximately 1-cm-diameter colony, at a cell density of n = 2.5 organisms per mm2. a, Final frame of Supplementary Video 11 after the trigger wave has passed. Coloured points indicate toxin particles released by different organisms in the colony. Grey organisms (ellipses) are triggered; black cells are not triggered. b, Trajectories of ten simulated toxin particles released by a single organism during a hydrodynamic trigger wave. Colours distinguish tracks of the different particles, black circles are the initial positions of the particles and the black points are the final positions of the particles. At the first contraction, the particles are mostly pulled inwards; with subsequent contractions of other cells, the particles follow a random walk and spread out.
Supplementary information
Supplementary Information
This file contains Supplementary Sections 1-7 – see contents page for details.
Supplementary Video 1
Close-up of metachronal waves, antisymplectic on top. Images are recorded at 40x magnification and 500fps (playback 10x slowed down). The organism swims between glass slides separated 100 microns. Added are D = 0.75 micron tracer particles to visualise the local flows generated by the swimming strokes. Ne = 18.
Supplementary Video 2
Montage of global flows generated by swimming. Images are recorded at 4x magnification and 500fps (playback 10x slowed down). The organism swims in a glass channel of height 100 microns, filled with D = 0.75 micron tracer particles. The FlowTrace algorithm [22] was used to convolve a superposition of 100 frames for each image. Ne = 38.
Supplementary Video 3
High-speed recording of body dynamics during contraction. Images are recorded at 20x magnification and 2,800fps (playback 50x slowed down). The contraction occurred ‘spontaneously’, so was not triggered electrically. Ne = 23.
Supplementary Video 4
High-speed recording of inertial flows generated during a contraction. Images are recorded at 10x magnification and 10,000fps (play- back 200x slowed down). The organism swims in an air-liquid-air film of 500 microns height, and was triggered by an electric pulse (|E| = 1.5kV/m, τE = 100ms) in the middle of the film. The Flow- Trace algorithm [22] was used to show streamlines by superimposing 200 frames for each image. Note the spreading of the 4 vortex centers into the liquid over time, cf. Video 5. Ne = 46.
Supplementary Video 5
Linearised Navier-Stokes solution of inertial flows generated during a contraction. The flow solution (Eq. 27) is evaluated in a 2x2mm domain during a 100ms period. The method of im- ages was used to satisfy the boundary conditions of an air-liquid-air film of 500 microns height. Yellow arrows are streamlines and background colours de- note the flow magnitude. Note the spreading of 4 vortices into the liquid over time, cf. Video 4.
Supplementary Video 6
Rheosensitivity measured in a microfluidic device. Images are recorded at 1.5x magnification and 1,000fps (playback 50x slowed down). As organisms are drawn towards the central flow outlet (red), the strain rate increases with decreasing radial position, ˙ = M/→2, where M is the flow rate. When the organism reaches the threshold (orange, h→ci = 3.22mm) its mechanosensitive channels open and the cell contracts. This high- throughput experiment is repeated for N > 100 cells to compute the average critical strain rate. Ne = 17.
Supplementary Video 7
Spontaneous clustering behaviour. Images are recorded at 1x magnification and 4fps (playback 10x speed up). The organisms swim to- wards one another after manual fluid mixing. A double group contraction is observed at cell high densities, at time point 5:30. Ne = 11.
Supplementary Video 8
Collective hydrodynamic signaling. Images are recorded at 4x magnification and 15,000fps (playback 150x slowed down). Contracting cells generate a flow that triggers other organisms. Superimposed on the experimental video is the evolution of the connectivity graph, showing which organism triggered which, where colors denote the contraction time. Ne = 41.
Supplementary Video 9
Percolation simulations of collective hydrodynamic signaling. A large number N (15, 000) of organisms (black lines) are distributed randomly over a circular cluster of radius R = 50mm. One central organism is triggered, and subsequent contraction dynamics are simulated over time (denoted by colors) until no more organisms move. (a) Just below the critical point, at density n = 1.75 [cells/mm2], the trigger wave decays very rapidly. (b) Near the critical point, at n = 2, many branches of the connectivity graph die out but one path reaches the cluster edge. (c) Just above the critical point, at n = 2.25, almost all organisms are triggered, readily establishing percolation. In summary, a 25% difference in density has a much larger effect on communication.
Supplementary Video 10
Simplified demonstration of wave speed dependence on organism density. Cells are arranged along the x axis with parallel (a) and perpendicular (b) orientations, separated a distance just small enough for signal transduction. At lower cell densities (a) the wave moves faster than higher densities (b), but at the cost of losing percolation by small orientation fluctuations. In this simplified case the cells can only trigger the nearest neighbours. In more complex configurations the hydro- dynamic screening at high cell densities has a similar effect.
Supplementary Video 11
Toxin mixing during a hydrodynamic trigger wave, simulated for N = 123 organisms in a colony of diameter D ← 1cm, at cell density n = 2.5 organisms/mm2. Coloured points indicate toxin particles released by different organisms in a colony. Grey organisms (ellipses) are triggered and black cells are not (yet) triggered.
Rights and permissions
About this article
Cite this article
Mathijssen, A.J.T.M., Culver, J., Bhamla, M.S. et al. Collective intercellular communication through ultra-fast hydrodynamic trigger waves. Nature 571, 560–564 (2019). https://doi.org/10.1038/s41586-019-1387-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1387-9
This article is cited by
-
Forces and Flows at Cell Surfaces
The Journal of Membrane Biology (2023)
-
Active carpets drive non-equilibrium diffusion and enhanced molecular fluxes
Nature Communications (2021)
-
Mechanomicrobiology: how bacteria sense and respond to forces
Nature Reviews Microbiology (2020)
-
Active hydrodynamic imaging of a rigid spherical particle
Scientific Reports (2020)
-
Understanding contagion dynamics through microscopic processes in active Brownian particles
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.