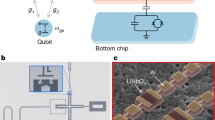
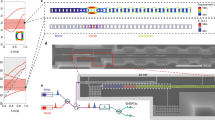
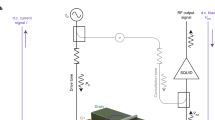
Abstract
The quantum nature of an oscillating mechanical object is anything but apparent. The coherent states that describe the classical motion of a mechanical oscillator do not have a well defined energy, but are quantum superpositions of equally spaced energy eigenstates. Revealing this quantized structure is only possible with an apparatus that measures energy with a precision greater than the energy of a single phonon. One way to achieve this sensitivity is by engineering a strong but nonresonant interaction between the oscillator and an atom. In a system with sufficient quantum coherence, this interaction allows one to distinguish different energy eigenstates using resolvable differences in the atom’s transition frequency. For photons, such dispersive measurements have been performed in cavity1,2 and circuit quantum electrodynamics3. Here we report an experiment in which an artificial atom senses the motional energy of a driven nanomechanical oscillator with sufficient sensitivity to resolve the quantization of its energy. To realize this, we build a hybrid platform that integrates nanomechanical piezoelectric resonators with a microwave superconducting qubit on the same chip. We excite phonons with resonant pulses and probe the resulting excitation spectrum of the qubit to observe phonon-number-dependent frequency shifts that are about five times larger than the qubit linewidth. Our result demonstrates a fully integrated platform for quantum acoustics that combines large couplings, considerable coherence times and excellent control over the mechanical mode structure. With modest experimental improvements, we expect that our approach will enable quantum nondemolition measurements of phonons4 and will lead to quantum sensors and information-processing approaches5 that use chip-scale nanomechanical devices.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets generated and analysed for the current study are available from the corresponding author on reasonable request.
References
Brune, M. et al. From Lamb shift to light shifts: vacuum and subphoton cavity fields measured by atomic phase sensitive detection. Phys. Rev. Lett. 72, 3339–3342 (1994).
Bertet, P. et al. Direct measurement of the Wigner function of a one-photon Fock state in a cavity. Phys. Rev. Lett. 89, 200402 (2002).
Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007).
Braginsky, V. B. & Khalili, F. Y. Quantum nondemolition measurements: the route from toys to tools. Rev. Mod. Phys. 68, 1–11 (1996).
Ofek, N. et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441–445 (2016).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Gustafsson, M. V. et al. Propagating phonons coupled to an artificial atom. Science 346, 207–211 (2014).
Cohen, J. D. et al. Phonon counting and intensity interferometry of a nanomechanical resonator. Nature 520, 522–525 (2015).
Riedinger, R. et al. Non-classical correlations between single photons and phonons from a mechanical oscillator. Nature 530, 313–316 (2016).
Chu, Y. et al. Creation and control of multi-phonon Fock states in a bulk acoustic-wave resonator. Nature 563, 666–670 (2018).
Satzinger, K. J. et al. Quantum control of surface acoustic-wave phonons. Nature 563, 661–665 (2018).
Viennot, J. J., Ma, X. & Lehnert, K. W. Phonon-number-sensitive electromechanics. Phys. Rev. Lett. 121, 183601 (2018).
Mabuchi, H. Cavity quantum electrodynamics: coherence in context. Science 298, 1372–1377 (2002).
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013).
Chu, Y. et al. Quantum acoustics with superconducting qubits. Science 358, 199–202 (2017).
Thompson, J. D. et al. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 452, 72–75 (2008).
Miao, H., Danilishin, S., Corbitt, T. & Chen, Y. Standard quantum limit for probing mechanical energy quantization. Phys. Rev. Lett. 103, 100402 (2009).
Ludwig, M., Safavi-Naeini, A. H., Painter, O. & Marquardt, F. Enhanced quantum nonlinearities in a two-mode optomechanical system. Phys. Rev. Lett. 109, 063601 (2012).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Brune, M., Haroche, S., Lefevre, V., Raimond, J. M. & Zagury, N. Quantum nondemolition measurement of small photon numbers by Rydberg-atom phase-sensitive detection. Phys. Rev. Lett. 65, 976–979 (1990).
Lachance-Quirion, D. et al. Resolving quanta of collective spin excitations in a millimeter-sized ferromagnet. Sci. Adv. 3, e1603150 (2017).
Ioffe, L. B., Geshkenbein, V. B., Helm, C. & Blatter, G. Decoherence in superconducting quantum bits by phonon radiation. Phys. Rev. Lett. 93, 057001 (2004).
Barends, R. et al. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013).
Gambetta, J. et al. Qubit-photon interactions in a cavity: measurement-induced dephasing and number splitting. Phys. Rev. A 74, 042318 (2006).
Schuster, D. I. et al. ac Stark shift and dephasing of a superconducting qubit strongly coupled to a cavity field. Phys. Rev. Lett. 94, 123602 (2005).
Safavi-Naeini, A. H. & Painter, O. Proposal for an optomechanical traveling wave phonon–photon translator. New J. Phys. 13, 013017 (2011).
Bochmann, J., Vainsencher, A., Awschalom, D. D. & Cleland, A. N. Nanomechanical coupling between microwave and optical photons. Nat. Phys. 9, 712–716 (2013).
MacCabe, G. S. et al. Phononic bandgap nano-acoustic cavity with ultralong phonon lifetime. Preprint at http://arxiv.org/abs/1901.04129 (2019).
Pechal, M., Arrangoiz-Arriola, P. & Safavi-Naeini, A. H. Superconducting circuit quantum computing with nanomechanical resonators as storage. Quantum Sci. Technol. 4, 015006 (2018).
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 342, 607–610 (2013).
Sletten, L. D. et al. Resolving phonon Fock states in a multimode cavity with a double-slit qubit. Phys. Rev. X 9, 021056 (2019).
Wang, C. et al. Integrated high quality factor lithium niobate microdisk resonators. Opt. Express 22, 30924–30933 (2014).
Dolan, G. J. Offset masks for liftoff photoprocessing. Appl. Phys. Lett. 31, 337–339 (1977).
Kelly, J. Fault-Tolerant Superconducting Qubits. PhD thesis, Univ. of California, Santa Barbara (2015); https://web.physics.ucsb.edu/~martinisgroup/theses/Kelly2015.pdf.
Dunsworth, A. et al. Characterization and reduction of capacitive loss induced by sub-micron Josephson junction fabrication in superconducting qubits. Appl. Phys. Lett. 111, 022601 (2017).
Vidal-Álvarez, G., Kochhar, A. & Piazza, G. Delay lines based on a suspended thin film of X-cut lithium niobate. In 2017 IEEE Int. Ultrasonics Symp. (IEEE, 2017).
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004).
COMSOL Multiphysics version 4.4 (2013); http://www.comsol.com.
Arrangoiz-Arriola, P. & Safavi-Naeini, A. H. Engineering interactions between superconducting qubits and phononic nanostructures. Phys. Rev. A 94, 063864 (2016).
Acknowledgements
We thank R. Patel, C. J. Sarabalis and A. Y. Cleland for useful discussions. This work was supported by the David and Lucile Packard Fellowship, the Stanford University Terman Fellowship and by the US government through the Office of Naval Research under MURI grant number N00014-151-2761 (QOMAND), the Army Research Office (ARO/LPS) through the CQTS programme, and by the National Science Foundation under grant number ECCS-1708734. P.A.-A. and J.D.W. were partially supported by a Stanford Graduate Fellowship, and E.A.W. was supported by the Department of Defense through a National Defense & Engineering Graduate Fellowship. M.P. ackowledges support from the Swiss National Science Foundation. Part of this work was performed at the Stanford Nano Shared Facilities (SNSF), supported by the National Science Foundation under grant number ECCS-1542152, and at the Stanford Nanofabrication Facility (SNF).
Author information
Authors and Affiliations
Contributions
P.A.-A. and E.A.W. designed and fabricated the device. P.A.-A., E.A.W., W.J., T.P.M., J.D.W. and R.V.L. developed the fabrication process. Z.W., M.P. and A.H.S.-N. provided experimental and theoretical support. P.A.-A. and E.A.W. performed the experiments and analysed the data. P.A.-A., E.A.W. and A.H.S.-N. wrote the manuscript, with Z.W. and M.P. assisting. P.A.-A. and A.H.S.-N. conceived the experiment, and A.H.S.-N. supervised all efforts.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Albert Schliesser and Swati Singh for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Experimental setup.
The sample is located at the mixing-chamber plate of a dilution refrigerator, packaged in a microwave printed circuit board with a copper enclosure, and surrounded by cryogenic magnetic shielding. All instruments are phase-locked by a 10-MHz rubidium frequency standard (SRS SIM940). HEMT, high-electron-mobility transistor.
Extended Data Fig. 2 Characterization of qubit and mechanical modes.
a, Rabi oscillation measurement used to calibrate the qubit excitation pulses. b, Energy relaxation of the qubit (green) and the mechanical system (blue), with lifetimes of T1 = 1.14 μs and 430 ns, respectively. This measurement of the qubit lifetime T1 was obtained at ωge/(2π) = 2.301 GHz. At this same frequency, we performed the ringdown measurement of the mechanical mode at \({\omega }_{{\rm{m}}}^{(1)}/\left(2{\rm{\pi }}\right)=2.405\,{\rm{GHz}}\).
Extended Data Fig. 3 Qubit frequency tracking.
a, Raw qubit-tracking spectrum, obtained at 1 h elapsed time. First, the bare qubit spectrum is averaged over a 20-s interval, with a full spectral measurement performed every about 1 ms; all of the raw 20-s tracking spectra taken during the hour-long experiment are overlaid (grey circles). Then, these spectra are averaged without post-processing to obtain the effective bare qubit spectrum (green curve), resulting in an effective linewidth of about 2.8 MHz. b, Qubit-tracking spectrum with post-processing. The same qubit spectra as in a, but each 20-s tracking spectrum is aligned to the average qubit frequency using post-processing peak detection. The effective qubit linewidth is now improved to about 1.1 MHz. c, Alignment of bare qubit spectra through time. Each horizontal slice represents a 20-s tracking spectrum, showing that the qubit drifts by ±1.5 MHz during the experiment. d, Raw phonon-number-splitting spectrum. We interleave phonon-number-splitting measurements between the tracking spectra shown in a, alternating between the two every about 0.5 ms. When all of the raw spectra (grey points) are averaged without frequency correction (green curve), phonon-number splitting is visible but the peaks are poorly resolved. e, Post-processed phonon-number-splitting spectrum. Using the frequency corrections applied in b, we adjust the frequencies of each slice and improve the resolution of the peaks. f, Alignment of phonon-number-splitting spectra through time. The zero- and one-phonon peaks are easily visible with a splitting of 2χ ≈ 3 MHz.
Extended Data Fig. 4 Phononic crystal resonator design.
a, Simulation geometries of the mirror cell (top) and defect cell (bottom). b, Complete band diagram (including all polarizations and symmetries) of the mirror regions. A bandgap over the approximate range [1.6 GHz, 2.0 GHz] is clearly visible. For these simulations we use the same mirror cell parameters as those of the fabricated devices: a = 1 μm, sl = 330 nm, sw = 150 nm, tAl = 50 nm, tLN = 230 nm and θsw = 11°. The discrepancy between the observed and simulated bandgap positions is not understood and could be attributed to a number of factors, including possible differences in the material constants of our LN films and those used for the simulations. c, Deformation u(r) (top) and electrostatic potential ϕ(r) (bottom) of a localized defect mode at ν ≈ 1.9 GHz. Here we use adef = 1.3 μm, wdef = 1.25 μm and lgap = 500 nm. The mode deformation is predominantly polarized in the plane of the phononic crystal, and the polarization generated by the piezoelectricity in LN is predominantly aligned along the direction of the electric field produced by the electrodes, as is evident by the electrostatic potential. d, Deformation of the same mode as that in c, with a view of the entire resonator. The colour indicates log10|u(r)|/|umax|, illustrating that even with N = 4 mirror cells the mode is tightly localized to the defect region. In the measured devices, N = 8. e, Imaginary part of the electromechanical admittance Ym(ω), obtained from finite-element simulations of the structure shown in d. Using Foster synthesis we extract the coupling rates g of each of the modes associated with the pole/zero pairs that are visible in the response. f, Frequency of the strongly coupled modes as a function of wdef. Their distribution (although not their absolute values) agrees fairly well with that of the observed modes.
Supplementary information
Supplementary Information
This file contains a detailed description of the numerical simulations that were performed to model the phonon number splitting experiment, and a discussion of the technique used to optimize the dispersive coupling rate. It also includes an additional phonon number splitting dataset.
Rights and permissions
About this article
Cite this article
Arrangoiz-Arriola, P., Wollack, E.A., Wang, Z. et al. Resolving the energy levels of a nanomechanical oscillator. Nature 571, 537–540 (2019). https://doi.org/10.1038/s41586-019-1386-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1386-x
This article is cited by
-
Engineering multimode interactions in circuit quantum acoustodynamics
Nature Physics (2024)
-
Sound interactions across multiple modes
Nature Physics (2024)
-
Surface modification and coherence in lithium niobate SAW resonators
Scientific Reports (2024)
-
Resolving Fock states near the Kerr-free point of a superconducting resonator
npj Quantum Information (2023)
-
Photonic van der Waals integration from 2D materials to 3D nanomembranes
Nature Reviews Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.