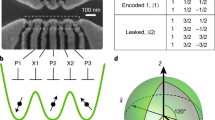
Abstract
Universal quantum computation will require qubit technology based on a scalable platform1, together with quantum error correction protocols that place strict limits on the maximum infidelities for one- and two-qubit gate operations2,3. Although various qubit systems have shown high fidelities at the one-qubit level4,5,6,7,8,9,10, the only solid-state qubits manufactured using standard lithographic techniques that have demonstrated two-qubit fidelities near the fault-tolerance threshold6 have been in superconductor systems. Silicon-based quantum dot qubits are also amenable to large-scale fabrication and can achieve high single-qubit gate fidelities (exceeding 99.9 per cent) using isotopically enriched silicon11,12. Two-qubit gates have now been demonstrated in a number of systems13,14,15, but as yet an accurate assessment of their fidelities using Clifford-based randomized benchmarking, which uses sequences of randomly chosen gates to measure the error, has not been achieved. Here, for qubits encoded on the electron spin states of gate-defined quantum dots, we demonstrate Bell state tomography with fidelities ranging from 80 to 89 per cent, and two-qubit randomized benchmarking with an average Clifford gate fidelity of 94.7 per cent and an average controlled-rotation fidelity of 98 per cent. These fidelities are found to be limited by the relatively long gate times used here compared with the decoherence times of the qubits. Silicon qubit designs employing fast gate operations with high Rabi frequencies16,17, together with advanced pulsing techniques18, should therefore enable much higher fidelities in the near future.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Knill, E. & Laflamme, R. Theory of quantum error-correcting codes. Phys. Rev. A 55, 900 (1997).
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012).
Kok, P. et al. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 79, 135 (2007).
Haffner, H., Roos, C. & Blatt, R. Quantum computing with trapped ions. Phys. Rep. 469, 155–203 (2008).
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014).
Rong, X. et al. Experimental fault-tolerant universal quantum gates with solid-state spins under ambient conditions. Nat. Commun. 6, 8748 (2015).
Muhonen, J. T. et al. Quantifying the quantum gate fidelity of single-atom spin qubits in silicon by randomized benchmarking. J. Phys. Condens. Matter 27, 154205 (2015).
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nature Nanotechnol. 9, 981–985 (2014).
Nichol, J. M. et al. High-fidelity entangling gate for double-quantum-dot spin qubits. npj Quant. Inform. 3, 3 (2017).
Itoh, K. M. & Watanabe, H. Isotope engineering of silicon and diamond for quantum computing and sensing applications. MRS Commun. 4, 143–157 (2014).
Ladd, T. D. & Carroll, M. S. Silicon qubits. In Encyclopedia of Modern Optics 2nd edn, 467–477 (Elsevier, 2018).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Zajac, D. M. et al. Resonantly driven cnot gate for electron spins. Science 359, 439–442 (2018).
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 9, 666–670 (2014).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102106 (2018).
Vandersypen, L. M. K. & Chuang, I. L. NMR techniques for quantum control and computation. Rev. Mod. Phys. 76, 1037–1069 (2005).
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431 (2004).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Koppens, F. H. L. et al. Driven coherent oscillations of a single electron spin in a quantum dot. Nature 442, 766–771 (2006).
Pioro-Ladrière, M. et al. Electrically driven single-electron spin resonance in a slanting Zeeman field. Nat. Phys. 4, 776779 (2008).
Golovach, V. N., Borhani, M. & Loss, D. Electric-dipole-induced spin resonance in quantum dots. Phys. Rev. B 74, 165319 (2006).
Maurand, R. et al. A CMOS silicon spin qubit. Nat. Commun. 7, 13575 (2016).
Huang, W., Veldhorst, M., Zimmerman, N. M., Dzurak, A. S. & Culcer, D. Electrically driven spin qubit based on valley mixing. Phys. Rev. B 95, 075403 (2017).
Corna, A. et al. Electrically driven electron spin resonance mediated by spin-valley-orbit coupling in a silicon quantum dot. npj Quant. Inform. 4, 6 (2018).
Nowack, K. C., Koppens, F. H. L., Nazarov, Y. V. & Vandersypen, L. M. K. Coherent control of a single electron spin with electric fields. Science 318, 1430–1433 (2007).
Yang, C. H. et al. Silicon qubit fidelities approaching incoherent noise limits via pulse engineering. Nat. Electron. 2, 151–158 (2019).
Nowack, K. C. et al. Single-shot correlations and two- qubit gate of solid-state spins. Science 333, 1269–1272 (2011).
Kalra, R., Laucht, A., Hill, C. D. & Morello, A. Robust two-qubit gates for donors in silicon controlled by hyperfine interactions. Phys. Rev. X 4, 021044 (2014).
Ryan, C., Laforest, M. & Laflamme, R. Randomized benchmarking of single- and multi-qubit control in liquid-state NMR quantum information processing. New J. Phys. 11, 013034 (2009).
Laucht, A. et al. A dressed spin qubit in silicon. Nat. Nanotechnol. 12, 6166 (2017).
Yang, C. H. et al. Spin-valley lifetimes in a silicon quantum dot with tunable valley splitting. Nat. Commun. 4, 2069 (2013).
Dehollain, J. P. et al. Nanoscale broadband transmission lines for spin qubit control. Nanotechnology 24, 015202 (2013).
Yang, C. H., Lim, W. H., Zwanenburg, F. A. & Dzurak, A. S. Dynamically controlled charge sensing of a few electron silicon quantum dot. AIP Adv. 1, 042111 (2011).
McKay, D. C., Wood, C. J., Sheldon, S., Chow, J. M. & Gambetta, J. M. Efficient z gates for quantum computing. Phys. Rev. A 96, 022330 (2017).
Sergeevich, A., Chandran, A., Combes, J., Bartlett, S. D. & Wiseman, H. M. Characterization of a qubit Hamiltonian using adaptive measurements in a fixed basis. Phys. Rev. A 84, 052315 (2011).
Shulman, M. D. et al. Suppressing qubit dephasing using real-time hamiltonian estimation. Nat. Commun. 5, 5156 (2014).
Delbecq, M. R. et al. Quantum dephasing in a gated gaas triple quantum dot due to nonergodic noise. Phys. Rev. Lett. 116, 046802 (2016).
Acknowledgements
We thank S. Bartlett, R. Harper, L. M. K. Vandersypen, T. D. Ladd and N. C. Jones for discussions. We acknowledge support from the US Army Research Office (W911NF-13-1-0024 and W911NF-17-1-0198), the Australian Research Council (CE170100012), and the NSW Node of the Australian National Fabrication Facility. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the US Government. The US Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. B.H. acknowledges support from the Netherlands Organization for Scientific Research (NWO) through a Rubicon Grant. K.M.I. acknowledges support from a Grant-in-Aid for Scientific Research by MEXT, NanoQuine, FIRST, and the JSPS Core-to-Core Program.
Reviewer information
Nature thanks Jason Petta and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
W.H. and C.H.Y. performed the experiments. K.W.C. and F.E.H. fabricated the devices. K.M.I. prepared and supplied the 28Si wafer. T.T. and J.C.C.H. contributed to the preparation of the experiments. W.H., C.H.Y., M.A.F., A.L. and B.H. designed the experiment and discussed the results. R.C.C.L. assisted with the data analysis. W.H., A.L. and A.S.D. wrote the manuscript with input from all co-authors. A.M., A.L. and A.S.D. planned and supervised the experiment.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Single-qubit coherence properties in the (1, 1) regime.
Blue data corresponds to Q1 and red data corresponds to Q2. We have characterized the single-qubit coherence properties \({T}_{2}^{\ast }\) and \({T}_{2}^{{\rm{Hahn}}}\), and measured their control fidelities via single-qubit randomized benchmarking. All data are acquired with the frequency feedback protocol described in Extended Data Fig. 2. a, Spin-up probability as a function of wait time in the Ramsey sequence. \({T}_{2,{\rm{Q}}2}^{\ast }=10.5\pm 1\,{\rm{\mu }}{\rm{s}}\) is much shorter than \({T}_{2,{\rm{Q}}1}^{\ast }=24.3\pm 2\,{\rm{\mu }}{\rm{s}}\). b, Spin-down probability as a function of wait time in the Hahn echo sequence. \({T}_{2,{\rm{Q}}2}^{{\rm{H}}{\rm{a}}{\rm{h}}{\rm{n}}}=33\pm 5\,{\rm{\mu }}{\rm{s}}\) is much shorter than \({T}_{2,{\rm{Q}}1}^{{\rm{H}}{\rm{a}}{\rm{h}}{\rm{n}}}=290\pm 40\,{\rm{\mu }}{\rm{s}}\). c, Single-qubit randomized benchmarking with the other qubit initialized in the \(\left|\downarrow \right\rangle \) state. Only the frequencies f1↓ and f2↓ are used for gate operations on Q1 and Q2 (single tone randomized benchmarking), respectively. The plot shows the projected state probability with increasing number of Clifford gates. The curve is fitted with \({P}_{\uparrow }=A(1-2{r}_{{\rm{C}}})+B\), and the Clifford gate fidelity is given by \({F}_{{\rm{Clifford}}}=1-{r}_{{\rm{C}}}\). The single-qubit Clifford gates are on average composed of 1.875 primitive π/2-pulses, so the π/2-pulse fidelity is extracted as \({F}_{{\rm{\pi }}/2}=1-{r}_{{\rm{C}}}/1.875\). The fidelity for all ESR pulses is in excess of 99%.
Extended Data Fig. 2 Frequency tracking protocol.
a, Frequency calibration of the ESR frequencies is implemented by interleaving calibration sequences with the randomized benchmarking experiment. After acquisition of three random sequences (one sequence is repeated 125 times), we check if the ESR frequency is still on-resonance by applying a low-power (26 dB lower than the typical operating power) π-rotation. If the spin-up probability is above the threshold of 50% of the readout visibility, the experiment will continue. If the spin-up probability is below the threshold, the resonance frequency will be recalibrated until all ESR frequencies pass the check, and the measurement will continue. More sophisticated frequency tracking schemes could also contribute to higher gate fidelities37,38,39. b, c, Resonance frequency fluctuations \({\rm{\Delta }}f={f}_{1\downarrow }-{f}_{{\rm{avg}}}\) of f1↓ (b) and \({\rm{\Delta }}f={f}_{2\downarrow }-{f}_{{\rm{avg}}}\) of f2↓ (c) during the measurement period. We subtracted the average values of the respective frequencies favg for better visibility. Over 13 h of data acquisition, Q1 experiences multiple jumps of about 600 kHz, while the fluctuations of Q2 remain within about 300 kHz. Since the resonance frequency fluctuations of Q1 and Q2 are uncorrelated, we exclude fluctuations of B0 or the microwave reference clock as the cause of the frequency changes. d, Variation of exchange coupling \({\rm{\Delta }}J=J-{J}_{{\rm{avg}}}\) during the measurement period. We subtracted the average value Javg for better visibility. The exchange coupling is relatively stable during the experiment. If the frequency fluctuations in b and c were to originate from charge noise, it is unlikely that J would remain unaffected. Furthermore, since the Stark shift of Q1 and Q2 is approximately 30 MHz V−1, a 600-kHz jump would require a change of the bias voltage applied to the D1 and D2 gates of about 20 mV. Such a change in the electrostatic environment would deteriorate qubit readout via the single-electron transistor charge sensor, but we noticed no substantial change of the readout level during the experiment. On this basis, we further exclude charge noise from being the cause of the frequency changes. We conclude that the frequency jumps are most probably caused by spin flips of residual 29Si nuclei that locally couple to the quantum dots.
Supplementary information
Supplementary Information
This file contains Supplementary Text, Supplementary Figures 1-4 and additional references.
Rights and permissions
About this article
Cite this article
Huang, W., Yang, C.H., Chan, K.W. et al. Fidelity benchmarks for two-qubit gates in silicon. Nature 569, 532–536 (2019). https://doi.org/10.1038/s41586-019-1197-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1197-0
This article is cited by
-
Anisotropic exchange interaction of two hole-spin qubits
Nature Physics (2024)
-
Hamiltonian phase error in resonantly driven CNOT gate above the fault-tolerant threshold
npj Quantum Information (2024)
-
High-fidelity spin qubit operation and algorithmic initialization above 1 K
Nature (2024)
-
Coherent spin–valley oscillations in silicon
Nature Physics (2023)
-
Compilation and scaling strategies for a silicon quantum processor with sparse two-dimensional connectivity
npj Quantum Information (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.