Abstract
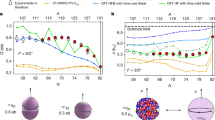
Nuclear magic numbers correspond to fully occupied energy shells of protons or neutrons inside atomic nuclei. Doubly magic nuclei, with magic numbers for both protons and neutrons, are spherical and extremely rare across the nuclear landscape. Although the sequence of magic numbers is well established for stable nuclei, experimental evidence has revealed modifications for nuclei with a large asymmetry between proton and neutron numbers. Here we provide a spectroscopic study of the doubly magic nucleus 78Ni, which contains fourteen neutrons more than the heaviest stable nickel isotope. We provide direct evidence of its doubly magic nature, which is also predicted by ab initio calculations based on chiral effective-field theory interactions and the quasi-particle random-phase approximation. Our results also indicate the breakdown of the neutron magic number 50 and proton magic number 28 beyond this stronghold, caused by a competing deformed structure. State-of-the-art phenomenological shell-model calculations reproduce this shape coexistence, predicting a rapid transition from spherical to deformed ground states, with 78Ni as the turning point.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
All of the relevant data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Wienholtz, F. et al. Masses of exotic calcium isotopes pin down nuclear forces. Nature 498, 346–349 (2013); erratum 500, 612 (2013).
Steppenbeck, D. et al. Evidence for a new nuclear “magic number” from the level structure of 54Ca. Nature 502, 207–210 (2013).
Erler, J. et al. The limits of the nuclear landscape. Nature 486, 509–512 (2012).
Haxel, O., Jensen, J. & Suess, H. On the “magic numbers” in nuclear structure. Phys. Rev. 75, 1766 (1949).
Goeppert Mayer, M. On closed shells in nuclei. Phys. Rev. 75, 1969–1970 (1949).
Navin, A. et al. Direct evidence of the breakdown of the N = 8 shell closure in 12Be. Phys. Rev. Lett. 85, 266–269 (2000).
Thibault, C. et al. Direct measurement of the mass of 11Li and 26–31Na with an on-line mass separator. Phys. Rev. C 12, 644–657 (1975).
Guillemaud-Mueller, D. et al. β decay schemes of very neutron-rich sodium isotopes and their descendants. Nucl. Phys. A 426, 37–76 (1984).
Bastin, B. et al. Collapse of the N = 28 shell closure in 42Si. Phys. Rev. Lett. 99, 022503 (2007).
Tshoo, K. et al. N = 16 spherical shell closure in 24O. Phys. Rev. Lett. 109, 022501 (2012).
Huck, A. et al. Beta decay of the new isotopes 52K, 52Ca, and 52Sc; a test of the shell model far from stability. Phys. Rev. C 31, 2226–2237 (1985).
Talmi, I. & Unna, I. Order of levels in the shell model and spin of 11Be. Phys. Rev. Lett. 4, 469–470 (1960).
Otsuka, T., Suzuki, T., Fujimoto, R., Grawe, H. & Akaishi, Y. Evolution of the nuclear shells due to the tensor force. Phys. Rev. Lett. 95, 232502 (2005).
Otsuka, T. et al. Novel features of nuclear forces and shell evolution in exotic nuclei. Phys. Rev. Lett. 104, 012501 (2010).
Otsuka, T., Suzuki, T., Holt, J. D., Schwenk, A. & Akaishi, Y. Three-body forces and the limit of oxygen isotopes. Phys. Rev. Lett. 105, 032501 (2010).
Hammer, H.-W., Nogga, A. & Schwenk, A. Three-body forces: from cold atoms to nuclei. Rev. Mod. Phys. 85, 197–217 (2013).
Engelmann, C. et al. Production and identification of heavy Ni isotopes: evidence for the doubly magic nucleus \({\,}_{28}^{78}{\rm{Ni}}\). Z. Phys. A 352, 351–352 (1995).
Van de Walle, J. et al. Coulomb excitation of neutron-rich Zn isotopes: first observation of the \({2}_{1}^{+}\) state in 80Zn. Phys. Rev. Lett. 99, 142501 (2007).
Hakala, J. et al. Evolution of the N = 50 shell gap energy towards 78Ni. Phys. Rev. Lett. 101, 052502 (2008).
Mazzocchi, C. et al. Low energy structure of even-even Ni isotopes close to 78Ni. Phys. Lett. B 622, 45–54 (2005).
Hosmer, P. T. et al. Half-life of the doubly magic r-process nucleus 78Ni. Phys. Rev. Lett. 94, 112501 (2005).
Xu, Z. Y. et al. β-decay half-lives of 76,77Co, 79,80Ni and 81Cu: experimental indication of a doubly magic 78Ni. Phys. Rev. Lett. 113, 032505 (2014).
Sahin, E. et al. Shell evolution towards 78Ni: low-lying states in 77Cu. Phys. Rev. Lett. 118, 242502 (2017).
Olivier, L. et al. Persistence of the Z = 28 shell gap around 78Ni: first spectroscopy of 79Cu. Phys. Rev. Lett. 119, 192501 (2017).
Welker, A. et al. Binding energy of 79Cu: probing the structure of the doubly magic 78Ni from only one proton away. Phys. Rev. Lett. 119, 192502 (2017).
Hagen, G., Jansen, G. R. & Papenbrock, T. Structure of 78Ni from first-principles computations. Phys. Rev. Lett. 117, 172501 (2016).
Santamaria, C. et al. Extension of the N = 40 island of inversion towards N = 50: spectroscopy of 66Cr, 70,72Fe. Phys. Rev. Lett. 115, 192501 (2015).
Nowacki, F., Poves, A., Caurier, E. & Bounthong, B. Shape coexistence in 78Ni as the portal to the fifth island of inversion. Phys. Rev. Lett. 117, 272501 (2016).
Franchoo, S. et al. Beta-decay of 68–74Ni and level structure of neutron-rich Cu isotopes. Phys. Rev. Lett. 81, 3100–3103 (1998).
Flanagan, K. T. et al. Nuclear spins and magnetic moments of 71,73,75Cu: inversion of π2p 3/2 and π1f 5/2 levels in 75Cu. Phys. Rev. Lett. 103, 142501 (2009).
Sieja, K. & Nowacki F. Shell quenching in 78Ni: hint from the structure of neutron-rich copper isotopes. Phys. Rev. C 81, 061303 (2010).
Gottardo, A. et al. First evidence of shape coexistence in the 78Ni region: intruder \({0}_{2}^{+}\) state in 80Ge. Phys. Rev. Lett. 116, 182501 (2016).
Yang, X. F. et al. Isomer shift and magnetic moment of the long-lived 1/2+ isomer in \({\,}_{30}^{79}{{\rm{Zn}}}_{49}\): signature of shape coexistence near 78Ni. Phys. Rev. Lett. 116, 182502 (2016).
Kubo, T. et al. BigRIPS separator and ZeroDegree spectrometer at RIKEN RI Beam Factory. Prog. Theor. Phys. 2012, 03C003 (2012).
Obertelli, A. et al. MINOS: a vertex tracker coupled to a thick liquid-hydrogen target for in-beam spectroscopy of exotic nuclei. Eur. Phys. J. A 50, 8 (2014).
Takeuchi, S. et al. DALI2: a NaI(Tl) detector array for measurements of γ rays from fast nuclei. Nucl. Instr. Meth. Phys. Res. A 763, 596–603 (2014).
Sorlin, O. et al. 68Ni: magicity versus superfluidity. Phys. Rev. Lett. 88, 092501 (2002).
Guénaut, C. et al. High-precision mass measurements of nickel, copper, and gallium isotopes and the purported shell closure at N = 40. Phys. Rev. C 75, 044303 (2007).
Langanke, K., Terasaki, J., Nowacki, F., Dean, D. J. & Nazarewicz, W. How magic is the magic 68Ni nucleus? Phys. Rev. 67, 044314 (2003).
National Nuclear Data Center. Evaluated Nuclear Structure Data Files http://www.nndc.bnl.gov/ensdf/ (2018).
Lenzi, S. M., Nowacki, F., Poves, A. & Sieja, K. Island of inversion around 64Cr. Phys. Rev. C 82, 054301 (2010).
Shimizu, N. et al. New-generation Monte Carlo shell model for the K computer era. Prog. Theor. Exp. Phys. 2012, 01A205 (2012).
Tsunoda, Y., Otsuka, T., Shimizu, N., Honma, M. & Utsuno, Y. Novel shape evolution in exotic Ni isotopes and configuration-dependent shell structure. Phys. Rev. C 89, 031301 (2014).
Péru, S. & Martini, M. Mean field based calculations with the Gogny force: some theoretical tools to explore the nuclear structure. Eur. Phys. J. A 50, 88 (2014).
Goriely, S., Hilaire, S., Girod, M. & Péru, S. First Gogny–Hartree–Fock–Bogoliubov nuclear mass model. Phys. Rev. Lett. 102, 242501 (2009).
Stroberg, S. R. et al. Nucleus-dependent valence-space approach to nuclear structure. Phys. Rev. Lett. 118, 032502 (2017).
Hergert, H., Bogner, S. K., Morris, T. D., Schwenk, A. & Tsukiyama, K. The In-medium similarity renormalization group: a novel ab initio method for nuclei. Phys. Rep. 621, 165–222 (2016).
Epelbaum, E., Hammer, H.-W. & Meißner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys. 81, 1773–1825 (2009).
Wakasa, T., Ogata, K. & Noro, T. Proton-induced knockout reactions with polarized and unpolarized beams. Prog. Part. Nucl. Phys. 96, 32–87 (2017).
Wang, M. et al. The AME2016 atomic mass evaluation. Chin. Phys. C 41, 030003 (2017).
Okuno, H., Fukunishi, N. & Kamigaito, O. Progress of RIBF accelerators. Prog. Theor. Exp. Phys. 2012, 03C002 (2012).
Fukuda, N. et al. Identification and separation of radioactive isotope beams by the BigRIPS separator at the RIKEN RI Beam Factory. Nucl. Instr. Meth. Phys. Res. B 317, 323–332 (2013).
Baba, H. et al. New data acquisition system for the RIKEN Radioactive Isotope Beam Factory. Nucl. Instr. Meth. Phys. Res. A 616, 65–68 (2010).
Calvet, D. A versatile readout system for small to medium scale gaseous and silicon detectors. IEEE Trans. Nucl. Sci. 61, 675–682 (2014).
Baron, P. et al. Operational experience with the readout system of the MINOS vertex tracker. IEEE Trans. Nucl. Sci. 64, 1494–1500 (2017).
Doornenbal, P. In-beam gamma-ray spectroscopy at the RIBF. Prog. Theor. Phys. 2012, 03C004 (2012).
Santamaria, C. et al. Tracking with the MINOS Time Projection Chamber. Nucl. Instr. Meth. Phys. Res. A 905, 138–148 (2018).
Agostinelli, S. et al. GEANT4 – a simulation toolkit. Nucl. Instr. Meth. Phys. Res. A 506, 250–303 (2003).
Wraith, C. et al. Evolution of nuclear structure in neutron-rich odd-Zn isotopes and isomers. Phys. Lett. B 771, 385–391 (2017).
De Groote, R.P. et al. Dipole and quadrupole moments of 73–78Cu as a test of the robustness of the Z = 28 shell closure near 78Ni. Phys. Rev. C 96, 041312 (2017).
Shand, C. M. et al. Shell evolution beyond Z = 28 and N = 50: spectroscopy of 81,82,83,84Zn. Phys. Lett. B 773, 492–497 (2017).
Cortés, M. L. et al. Inelastic scattering of neutron-rich Ni and Zn isotopes off a proton target. Phys. Rev. C 97, 044315 (2018).
Whitehead, R. R. in Theory and Applications of Moments Methods in Many Fermion Systems (eds Dalton, B. J. et al.), 235–255, (Plenum, New York, 1980).
Caurier, E., Martínez-Pinedo, G., Nowacki, F., Poves, A. & Zuker, A. P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 77, 427–488 (2005).
Leoni, S. et al. Multifaceted quadruplet of low-lying spin-zero states in 66Ni: emergence of shape isomerism in light nuclei. Phys. Rev. Lett. 118, 162502 (2017).
Suchyta, S. et al. Shape coexistence in 68Ni. Phys. Rev. C 89, 021301 (2014).
Flavigny, F. et al. Characterization of the low-lying 0+ and 2+ states in 68Ni via β decay of the low-spin 68Co isomer. Phys. Rev. C 91, 034310 (2015).
Chiara, C. J. et al. Identification of deformed intruder states in semi-magic 70Ni. Phys. Rev. C 91, 044309 (2015).
Morales, A. I. et al. Type II shell evolution in A = 70 isobars from the N≥40 island of inversion. Phys. Lett. B 765, 328–333 (2017).
Tsukiyama, K., Bogner, S. K. & Schwenk, A. In-medium similarity renormalization group for nuclei. Phys. Rev. Lett. 106, 222502 (2011).
Morris, T. D., Parzuchowski, N. M. & Bogner, S. K. Magnus expansion and in-medium similarity renormalization group. Phys. Rev. C 92, 034331 (2015).
Tsukiyama, K., Bogner, S.K. & Schwenk, A. In-medium similarity renormalization group for open-shell nuclei. Phys. Rev. C 85, 061304 (2012).
Bogner, S. K. et al. Nonperturbative shell-model interactions from the in-medium similarity renormalization group. Phys. Rev. Lett. 113, 142501 (2014).
Stroberg, S.R., Hergert, H., Holt, J.D., Bogner, S.K. & Schwenk, A. Ground and excited states of doubly open-shell nuclei from ab initio valence-space Hamiltonians. Phys. Rev. C 93, 051301 (2016).
Hebeler, K., Bogner, S.K., Furnstahl, R.J., Nogga, A. & Schwenk, A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys. Rev. C 83, 031301 (2011).
Morris, T. D. et al. Structure of the lightest tin isotopes. Phys. Rev. Lett. 120, 152503 (2018).
Simonis, J. et al. Saturation with chiral interactions and consequences for finite nuclei. Phys. Rev. C 96, 014303 (2017).
Péru, S. & Goutte, H. Role of deformation on giant resonances within the quasiparticle random-phase approximation and the Gogny force. Phys. Rev. C 77, 044313 (2008).
Gaudefroy, L. et al. Collective structure of the N = 40 isotones. Phys. Rev. C 80, 064313 (2009).
Anguiano, M., Egido, J. L. & Robledo, L. M. Coulomb exchange and pairing contributions in nuclear Hartree–Fock–Bogoliubov calculations with the Gogny force. Nucl. Phys. A 683, 227–254 (2001).
Amos, K., Dortmans, P. J., von Geramb, H. V., Karataglidis, S. & Raynal, J. in Advanced Nuclear Physics Vol. 25 (eds Negele, J. W. & Vogt, E.) 276–536 (Plenum, New York, 2000).
Bohr, A. & Mottelson, B. R. Nuclear Structure Vol. I (Benjamin, New York, 1969).
Perey, F. G. & Buck, B. A non-local potential model for the scattering of neutrons by nuclei. Nucl. Phys. 32, 353–380 (1962).
Franey, M. A. & Love, W. G. Nucleon-nucleon t-matrix interaction for scattering at intermediate energies. Phys. Rev. C 31, 488–498 (1985).
Acknowledgements
We thank the staff of the RIKEN Nishina Center accelerator complex for providing a stable and high-intensity uranium beam and the BigRIPS team for the smooth operation of the secondary beams. We also thank N. Miyauchi for 3D schematic of the RIBF facility shown in Fig. 2a. The development of MINOS and the core MINOS team have been supported by the European Research Council through ERC grant number MINOS-258567. R.T. was supported by JSPS Grant-in-Aid for JSPS Research Fellows JP14J08717. A.O. was supported by JSPS long-term fellowship L-13520 at the RIKEN Nishina Center. C. Santamaria was supported by the IPA programme at the RIKEN Nishina Center. J.D.H. acknowledges support by the National Research Council of Canada and NSERC. This work was supported in part by the ERC through grant number 307986 STRONGINT, the DFG under grant SFB 1245 and the BMBF under contract number 05P18RDFN1. The MCSM calculations were performed on the K computer at RIKEN AICS (hp160211, hp170230, hp180179). J.M., T.O. and Y.T. acknowledge support from MEXT as ‘Priority Issue on post-K computer’ (Elucidation of the Fundamental Laws and Evolution of the Universe) and JICFuS. J.M. and K.O. were supported by Grant-in-Aid for Scientific Research JP18K03639 (J.M.) and JP16K05352 (K.O.). A. Poves acknowledges support by Mineco (Spain) grants FPA2014-57916 and Severo Ochoa Program SEV-2016-0597. This work was supported in part by the DFG through the Cluster of Excellence PRISMA. L.X.C. was supported by Vietnam MOST through the Physics Development Program grant TLCN.25/18. Z.D., Z.K. and Z.V. acknowledge support from the GINOP-2.3.3-15-2016-00034 project. M.L, C.L and V.W. acknowledge support from the German BMBF through grants 05P15RDNF1 and 05P12RDNF8.
Author information
Authors and Affiliations
Contributions
R.T. performed offline data analyses and GEANT4 simulations and prepared the figures; P.D. and A.O. designed the experiment; R.T., C. Santamaria, P.D., A.O., J.D.H., J.M., F.N., K.O., T.O., A.S. and Y.T. wrote the manuscript; R.T., C. Santamaria, P.D., A.O., G.A., D.C., F.C., A.C., A.D., J.-M.G., A.G., V.L., M.M., S.M., M.N., C.P., A. Peyaud, E.C.P., J.-Y.R., Y.S., S.T. and H.W. were responsible for setting up the liquid-hydrogen target, the vertex reconstruction system, MINOS and the γ-ray detector array, DALI2; R.T., C. Santamaria, H.B., D.C., A.C. and T.I. were responsible for the data acquisition system and analysis software; R.T., C. Santamaria, P.D., A.O., G.A., H.B., D.C., F.C., A.C., A.D., J.-M.G., A.G., T.I., V.L., M.M., S.M., M.N., H.O., C.P., A. Peyaud, E.C.P., J.-Y.R., Y.S., S.T., H.W., F.B., L.X.C., Z.D., S.F., F.G., A.G., K.H., Z.K., S.K., J.L., M.L., C.L., R.L., K.N., T. Miyazaki, S.N., L.O., S.O., Z.P., E.S., C. Shand, P.-A.S., I.S., D. Steppenbeck, T.S., D. Suzuki, Z.V., V.W., J.W. and Z.Y.X. checked the data accumulation online and maintained operation of the experiment; P.D., A.O., K.Y., T. Motobayashi, H.S. and T.U. supervised the participants; F.N. and A. Poves performed the LSSM calculations; T.O. and Y.T. performed the MCSM calculations; S.P. performed the QRPA calculations; J.D.H., J.M., A.S., J.S. and S.R.S. performed the IM-SRG calculations; K.O. performed the DWIA calculations. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Energy spectra of prompt γ-ray coincidences with 79Cu(p, 2p)78Ni reactions.
a, As in Fig. 3a, but with a binning of 40 keV, which allows us to resolve the transition at 583 keV. b, γ-ray spectrum in coincidence with the 583-keV transition. The expected intensities for coincidences with the 583-keV transition are indicated by the simulated lineshapes with and without the 1,103-keV transition, shown by the blue dashed and magenta solid lines, respectively. The results reveal no coincidence between the 583- and 1,103-keV transitions. c, γ-ray spectrum in coincidence with the 1,103-keV transition. The hypothesis of no coincidence between the 583- and 1,103-keV transitions is corroborated. Coincidence ranges are illustrated by the shaded areas in b and c.
Extended Data Fig. 2 Evolution of peak significance and fitted intensities as a function of γ-ray multiplicity.
a, b, Number of emitted γ-rays obtained for the fitted individual transitions. c, d, S.L. of individual transitions for the 79Cu(p, 2p)78Ni (c) and 80Zn(p, 3p)78Ni (d) reactions.
Rights and permissions
About this article
Cite this article
Taniuchi, R., Santamaria, C., Doornenbal, P. et al. 78Ni revealed as a doubly magic stronghold against nuclear deformation. Nature 569, 53–58 (2019). https://doi.org/10.1038/s41586-019-1155-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1155-x
This article is cited by
-
Demonstration of nuclear gamma-ray polarimetry based on a multi-layer CdTe Compton camera
Scientific Reports (2024)
-
Nuclear shell-model simulation in digital quantum computers
Scientific Reports (2023)
-
Experimental studies on the doubly magic \(^{100}\)Sn and neighboring \(N \approx Z\) nuclei with EURICA
Journal of the Korean Physical Society (2023)
-
First observation of 28O
Nature (2023)
-
Nuclear moments of indium isotopes reveal abrupt change at magic number 82
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.