Abstract
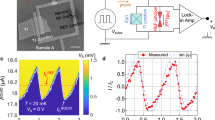
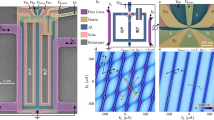
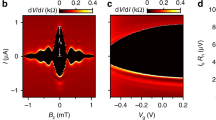
Topological superconductors can support localized Majorana states at their boundaries1,2,3,4,5. These quasi-particle excitations obey non-Abelian statistics that can be used to encode and manipulate quantum information in a topologically protected manner6,7. Although signatures of Majorana bound states have been observed in one-dimensional systems, there is an ongoing effort to find alternative platforms that do not require fine-tuning of parameters and can be easily scaled to large numbers of states8,9,10,11,12,13,14,15,16,17,18,19,20,21. Here we present an experimental approach towards a two-dimensional architecture of Majorana bound states. Using a Josephson junction made of a HgTe quantum well coupled to thin-film aluminium, we are able to tune the transition between a trivial and a topological superconducting state by controlling the phase difference across the junction and applying an in-plane magnetic field22. We determine the topological state of the resulting superconductor by measuring the tunnelling conductance at the edge of the junction. At low magnetic fields, we observe a minimum in the tunnelling spectra near zero bias, consistent with a trivial superconductor. However, as the magnetic field increases, the tunnelling conductance develops a zero-bias peak, which persists over a range of phase differences that expands systematically with increasing magnetic field. Our observations are consistent with theoretical predictions for this system and with full quantum mechanical numerical simulations performed on model systems with similar dimensions and parameters. Our work establishes this system as a promising platform for realizing topological superconductivity and for creating and manipulating Majorana modes and probing topological superconducting phases in two-dimensional systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data Availability
The data that support the findings of this study are available within the paper and its Supplementary Information. Additional data are available from the corresponding author upon request.
References
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys. Uspekhi 44, 131–136 (2001).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor–superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Oreg, Y., Refael, G. & von Oppen, F. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter. Phys. 4, 113–136 (2013).
Kitaev, A. Y. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003).
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008).
Stanescu, T. D., Lutchyn, R. M. & Das Sarma, S. Majorana fermions in semiconductor nanowires. Phys. Rev. B 84, 144522 (2011).
Mourik, V. et al. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 336, 1003–1007 (2012).
Zhang, H. et al. Quantized Majorana conductance. Nature 556, 74–79 (2018).
Nadj-Perge, S. et al. Observation of Majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Li, J., Neupert, T., Bernevig, B. A. & Yazdani, A. Manipulating Majorana zero modes on atomic rings with an external magnetic field. Nat. Commun. 7, 10395 (2016).
Shabani, J. et al. Two-dimensional epitaxial superconductor–semiconductor heterostructures: a platform for topological superconducting networks. Phys. Rev. B 93, 155402 (2016).
Rokhinson, L. P., Liu, X. & Furdyna, J. K. The fractional a.c. Josephson effect in a semiconductor–superconductor nanowire as a signature of Majorana particles. Nat. Phys. 8, 795–799 (2012).
Churchill, H. O. H. et al. Superconductor-nanowire devices from tunneling to the multichannel regime: zero-bias oscillations and magnetoconductance crossover. Phys. Rev. B 87, 241401 (2013).
Das, A. et al. Zero-bias peaks and splitting in an Al–InAs nanowire topological superconductor as a signature of Majorana fermions. Nat. Phys. 8, 887–895 (2012).
Finck, A. D. K., Van Harlingen, D. J., Mohseni, P. K., Jung, K. & Li, X. Anomalous modulation of a zero-bias peak in a hybrid nanowire-superconductor device. Phys. Rev. Lett. 110, 126406 (2013).
Albrecht, S. M. et al. Exponential protection of zero modes in Majorana islands. Nature 531, 206–209 (2016).
Chen, J. et al. Experimental phase diagram of zero-bias conductance peaks in superconductor/semiconductor nanowire devices. Sci. Adv. 3, e1701476 (2017).
Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).
Gül, Ö. et al. Ballistic Majorana nanowire devices. Nat. Nanotechnol. 13, 192–197 (2018).
Pientka, F. et al. Topological superconductivity in a planar Josephson junction. Phys. Rev. X 7, 021032 (2017).
Majorana, E. A symmetric theory of electrons and positrons. Nuovo Cimento 14, 171–184 (1937).
Karzig, T. et al. Scalable designs for quasiparticle-poisoning-protected topological quantum computation with Majorana zero modes. Phys. Rev. B 95, 235305 (2017).
Delfanazari, K. et al. On-chip Andreev devices: hard superconducting gap and quantum transport in ballistic Nb–In0.75Ga0.25As-quantum-well–Nb Josephson junctions. Adv. Mater. 29, 1701836 (2017).
Andreev, A. F. The thermal conductivity of the intermediate state in superconductors. Sov. Phys. JETP 19, 1228–1231 (1964).
Beenakker, C. W. J. & van Houten, H. Josephson current through a superconducting quantum point contact shorter than the coherence length. Phys. Rev. Lett. 66, 3056–3059 (1991).
Hart, S. et al. Induced superconductivity in the quantum spin Hall edge. Nat. Phys. 10, 638–643 (2014).
Hart, S. et al. Controlled finite momentum pairing and spatially varying order parameter in proximitized HgTe quantum wells. Nat. Phys. 13, 87–93 (2017).
Bretheau, L. et al. Tunnelling spectroscopy of Andreev states in graphene. Nat. Phys. 13, 756–760 (2017).
Groth, C. W., Wimmer, M., Akhmerov, A. R. & Waintal, X. Kwant: a software package for quantum transport. New J. Phys. 16, 063065 (2014).
Acknowledgements
This work is supported by the NSF DMR-1708688, by the STC Center for Integrated Quantum Materials under NSF grant number DMR-1231319, and by the NSF GRFP under grant DGE1144152. This work is also partly supported by the US Army Research Office and was accomplished under grant W911NF-18-1-0316. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the US Government. The US Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. A.T.P. is supported by the US Department of Defense through the National Defense Science and Engineering Graduate Fellowship Program. The work at the University of Würzburg is supported by the German Research Foundation (Leibniz Program, Sonderforschungsbereich 1170 ‘ToCoTronics’; Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter, ct.qmat, EXC 2147, project 39085490), the EU ERC-AG programme (Project 4-TOPS) and the Bavarian Ministry of Education, Science and the Arts (IDK Topologische Isolatoren and ITI research initiative).
Reviewer information
Nature thanks Kaveh Delfanazari and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
The experiment is a collaboration between the Harvard and Würzburg experimental groups. A.Y. conceived the experiment and supervised the project. L.L., R.S. and L.W.M. grew the material. H.R., S.H. and A.T.P. fabricated the devices. H.R., S.H., A.T.P. and M.K. performed the measurements. H.R., F.P., B.S., E.M.H., B.I.H. and A.Y. carried out the theoretical modelling and analysis and prepared the manuscript and Supplementary Information.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Methods and Notes, including a table of contents at the beginning and a list of 22 Supplementary Figures. The display items contain further explanation of our experimental and analytical methods, raw and additional data to support the conclusions presented in the main text, as well as detailed theoretical discussions on our modeling of the current and future devices.
Rights and permissions
About this article
Cite this article
Ren, H., Pientka, F., Hart, S. et al. Topological superconductivity in a phase-controlled Josephson junction. Nature 569, 93–98 (2019). https://doi.org/10.1038/s41586-019-1148-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1148-9
This article is cited by
-
Superconducting tunnel junctions with layered superconductors
Quantum Frontiers (2024)
-
Hard superconducting gap in germanium
Communications Materials (2023)
-
Phase-dependent Andreev molecules and superconducting gap closing in coherently-coupled Josephson junctions
Nature Communications (2023)
-
Realization of a minimal Kitaev chain in coupled quantum dots
Nature (2023)
-
The superconducting diode effect
Nature Reviews Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.