Abstract
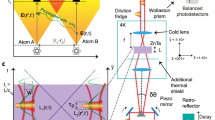
Quantum mechanics ascribes to the ground state of the electromagnetic radiation1 zero-point electric field fluctuations that permeate empty space at all frequencies. No energy can be extracted from the ground state of a system, and therefore these fluctuations cannot be measured directly with an intensity detector. The experimental proof of their existence therefore came from more indirect evidence, such as the Lamb shift2,3,4, the Casimir force between close conductors5,6,7 or spontaneous emission1,8. A direct method of determining the spectral characteristics of vacuum field fluctuations has so far been missing. Here we perform a direct measurement of the field correlation on these fluctuations in the terahertz frequency range by using electro-optic detection9 in a nonlinear crystal placed in a cryogenic environment. We investigate their temporal and spatial coherence, which, at zero time delay and spatial distance, has a peak value of 6.2 × 10−2 volts squared per square metre, corresponding to a fluctuating vacuum field10,11 of 0.25 volts per metre. With this measurement, we determine the spectral components of the ground state of electromagnetic radiation within the bandwidth of our electro-optic detection.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Loudon, R. The Quantum Theory of Light (Oxford Univ. Press, Oxford, 2000).
Lamb, W. E. Jr. & Retherford, R. C. Fine structure of the hydrogen atom by a microwave method. Phys. Rev. 72, 241–243 (1947).
Bethe, H. A. The electromagnetic shift of energy levels. Phys. Rev. 72, 339–341 (1947).
Fragner, A. et al. Resolving vacuum fluctuations in an electrical circuit by measuring the Lamb shift. Science 322, 1357–1360 (2008).
Casimir, H. B. G. On the attraction between two perfectly conducting plates. Indag. Math. 10, 261–263 (1948).
Moore, G. T. Quantum theory of the electromagnetic field in a variable-length one-dimensional cavity. J. Math. Phys. 11, 2679–2691 (1970).
Wilson, C. M. et al. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 479, 376–379 (2011).
Walls, D. & Milburn, G. Quantum Optics ch. 10 (Springer, 1994).
Wu, Q. & Zhang, X. C. Free-space electro-optic sampling of terahertz beams. Appl. Phys. Lett. 67, 3523–3525 (1995).
Riek, C. et al. Direct sampling of electric-field vacuum fluctuations. Science 350, 420–423 (2015).
Riek, C. et al. Subcycle quantum electrodynamics. Nature 541, 376–379 (2017).
Purcell, E. M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 69, 681 (1946).
Scalari, G. et al. Ultrastrong coupling of the cyclotron transition of a 2D electron gas to a THz metamaterial. Science 335, 1323–1326 (2012).
Keller, J. et al. Few-electron ultrastrong light–matter coupling at 300 GHz with nanogap hybrid LC microcavities. Nano Lett. 17, 7410–7415 (2017).
Bayer, A. et al. Terahertz light–matter interaction beyond unity coupling strength. Nano Lett. 17, 6340–6344 (2017).
Ciuti, C., Bastard, G. & Carusotto, I. Quantum vacuum properties of the intersubband cavity polariton field. Phys. Rev. B 72, 115303 (2005).
Günter, G. et al. Sub-cycle switch-on of ultrastrong light–matter interaction. Nature 458, 178 –181 (2009).
Benea-Chelmus, I.-C. et al. Subcycle measurement of intensity correlations in the terahertz frequency range. Phys. Rev. A 93, 043812–043819 (2016).
Benea-Chelmus, I.-C., Rösch, M., Scalari, G., Beck, M. & Faist, J. Intensity autocorrelation measurements of frequency combs in the terahertz range. Phys. Rev. A 96, 033821–033828 (2017).
Moskalenko, A. S., Riek, C., Seletskiy, D. V., Burkard, G. & Leitenstorfer, A. Paraxial theory of direct electro-optic sampling of the quantum vacuum. Phys. Rev. Lett. 115, 263601–263605 (2015).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Khalili, F. Y. et al. Quantum back-action in measurements of zero-point mechanical oscillations. Phys. Rev. A 86, 033840 (2012).
Kwiat, P. G. et al. New high-intensity source of polarization-entangled photon pairs. Phys. Rev. Lett. 75, 4337–4341 (1995).
da Silva, M. P., Bozyigit, D., Wallraff, A. & Blais, A. Schemes for the observation of photon correlation functions in circuit QED with linear detectors. Phys. Rev. A 82, 043804 (2010).
Bozyigit, D. et al. Antibunching of microwave-frequency photons observed in correlation measurements using linear detectors. Nat. Phys. 7, 154–158 (2011).
Lähteenmäki, P., Paraoanu, G. S., Hassel, J. & Hakonen, P. J. Coherence and multimode correlations from vacuum fluctuations in a microwave superconducting cavity. Nat. Commun. 7, 12548 (2016).
Kizmann, M. et al. Subcycle squeezing of light from a time flow perspective. Preprint at https://arxiv.org/abs/1807.10519 (2018).
Benea-Chelmus, I.-C. et al. Three-dimensional phase modulator at telecom wavelength acting as a terahertz detector with an electro-optic bandwidth of 1.25 terahertz. ACS Photonics 5, 1398–1403 (2018).
Cong, K. et al. Dicke superradiance in solids. J. Opt. Soc. Am. B 33, C80–C101 (2016).
Hagenmüller, D., Schachenmayer, J., Schütz, S., Genes, C. & Pupillo, G. Cavity-enhanced transport of charge. Phys. Rev. Lett. 119, 223601 (2017).
Orgiu, E. et al. Conductivity in organic semiconductors hybridized with the vacuum field. Nat. Mater. 14, 1123–1129 (2015).
Rungsawang, R. et al. Intensity detection of terahertz quantum cascade laser radiation using electro-optic sampling. Appl. Phys. Lett. 93, 191111 (2008).
van Kolck, A. et al. Thermo-optic detection of terahertz radiation from a quantum cascade laser. Appl. Phys. Lett. 97, 251103 (2010).
Acknowledgements
This work was funded by the European Research Council (Advanced Grant, Quantum Metamaterials in the Ultra Strong Coupling Regime) and the Swiss National Science Foundation (grant 165639). We acknowledge the mechanical workshop at ETHZ. We acknowledge the contribution of M. Ernzer to the noise analysis tools, E. Mavrona to the design of opto-mechanical components and the extraction of the refractive index of ZnTe, and A. Imamoglu for discussions.
Author information
Authors and Affiliations
Contributions
I.-C.B.-C. and J.F. conceived and designed the experiments. I.-C.B.-C., F.F.S and G.S. built the experimental setup. I.-C.B.-C. developed the data acquisition system and noise suppression protocols. I.-C.B.-C. and F.F.S. performed the measurements. I.-C.B.-C., F.F.S. and J.F. analysed and interpreted the data. I.-C.B.-C., F.F.S. and J.F. derived the theory. J.F. was the scientific supervisor of this work. All authors discussed the results and contributed to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
About this article
Cite this article
Benea-Chelmus, IC., Settembrini, F.F., Scalari, G. et al. Electric field correlation measurements on the electromagnetic vacuum state. Nature 568, 202–206 (2019). https://doi.org/10.1038/s41586-019-1083-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1083-9
This article is cited by
-
Thin-film lithium niobate electro-optic terahertz wave detector
Scientific Reports (2024)
-
All-optical subcycle microscopy on atomic length scales
Nature (2024)
-
Integrated microcavity electric field sensors using Pound-Drever-Hall detection
Nature Communications (2024)
-
Perfect intrinsic squeezing at the superradiant phase transition critical point
Scientific Reports (2023)
-
Terahertz waveform synthesis in integrated thin-film lithium niobate platform
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.